In a well-shuffled 52-card deck, half the cards are red and half are black. If the number of red cards in the top half of the deck is added to the number of black cards in the bottom half of the deck, the sum is 30. How many red cards are in the top half? (Copyright mathleague.com.)
Many difficult problems that you come across can seem fairly straightforward, as frequently you have a good sense of where to start and what steps to take, even if each step is quite challenging. For some problems, though, the difficulty lies in not knowing at all what to do. In these cases it initially seems impossible to figure out how to get started.
To Tinker means to try possibilities and adjust your strategy based on what you’ve learned from your efforts. Tinkering is like trying to fit puzzle pieces together — you need to test out the pieces to see if they’ll fit, but even if it doesn’t work you now have a better sense of the shape of each piece.
The important thing is to do something, even if you aren’t at all sure it will be helpful. Make a start. Don’t be paralyzed by the problem. When you work on a math problem, as you tinker, you are gathering information — information that might lead to a solution or that might lead to a more interesting question.
Trying a specific example, even when the problem does not ask for one, is an example of tinkering. In the above problem, for instance, try just guessing the number of red cards that are in the top half of the deck, and see what you can figure out from there. Even though your first guess is likely to be wrong, that’s perfectly OK. If you pay attention to the numbers you get for the amount of red and black cards in each half of the deck, you can adjust and make a much more educated guess the next time. That is, sometimes you will not notice a pattern until you generate some data for yourself.
Tinkering is a way of making abstract ideas and hard to approach problems concrete, so that you can really see what is going on.
The next few pages have a couple of problems for you to Tinker with. After you have tried a few different approaches, you can turn over the page and see if the solution provided was similar to yours, or if perhaps you came up with a better way!
Let’s start with a bit of a mystery:
Each letter in the addition problem below represents a different number.
$\begin{align} AB& \\ \underline{+\quad BC}& \\ ADD& \end{align}$
What are the only possible values of $A$, $B$, $C$, and $D$? Try solving it before you turn over the page.
After perhaps tinkering with a number of different random values for $A$, $B$, $C$, and $D$, just to see what seems to be working and what isn’t, you may have noticed that there is only one plausible value for $A$. What is it?
So now our problem has turned into:
$\begin{align} 1B& \\ \underline{+\quad BC}& \\ 1DD& \end{align}$
Could $B$ be 7 or lower?
If you conclude that $B$ is greater than 7, then it must be 8 or 9. So tinker a bit here. Replace $B$ by 9 and see what happens.
The problem would then be:
$\begin{align} 19& \\ \underline{+\quad 9C}& \\ 1DD& \end{align}$
Now what could $D$ be? How about $C$? (Remember we were told all the letters represented different digits.)
At this point you might have seen that $B$ must be 8. Now find $C$ and $D$, and be sure to check that your solution works.
Here’s a logic puzzle that might drive you a bit crazy at first, but you’ll find the solution quite satisfying:
- Al says: Bob is lying.
- Bob says: Carl is lying.
- Carl says: Al and Bob are both lying.
Who is lying? Who is telling the truth? There is only one possible answer.
If this seems impossible to solve, try just guessing right from the start who is telling the truth and who is lying, and see if your answer is consistent with what all three people are saying. If your initial answer doesn’t work, then adjust your guess and try again.
The answer is on the back of this page.
There is no question that this problem can tie you up in logical knots! Let’s try to approach it by assuming Al is telling the truth, and we’ll see where that gets us. If this assumption works, great! And if it doesn’t, hopefully we will have learned some valuable information about the problem.
If Al is telling the truth, that means that Bob is lying.
If Bob is lying, that means that he is lying about Carl lying, which means that Carl is telling the truth.
Now if Carl is telling the truth, that would mean that Al and Bob would both have to be lying. But we assumed at the start that Al was telling the truth! Al can’t both be telling the truth and lying. Our assumption that Al was telling the truth causes us to contradict ourselves, so it must be wrong. Therefore, since Al can’t be telling the truth, Al must be lying.
But does the problem really work out if Al is lying? Test it out and see.
So, who is lying, and who is telling the truth?
In case you were wondering if you could have started solving this problem by assuming, say, that Carl was telling the truth, and following the consequences from there, the answer is yes, absolutely. There are many ways to solve this problem, just as with many other math problems. The key is that all these different methods will eventually end up with the same answer.
The next few pages have a variety of “Tinker” problems for you to enjoy. Have fun!
Fill in the numbers $1$,$2$,$3$,$4$,$5$ once each, to make the equation true: $ \,?\, \times \,?\, - \,?\, \times \,?\, + \,?\, = - 13$.
If someone multiplied the first 211 primes together what would be the units digit of the product?
Add two numbers to the following set of numbers to make the mean 15 and the median 8.
$\left\{ {3,4,17,8,39,10,2,3,71,14} \right\}$
The 3 missing numbers (all possibly different) in the equation below add up to what?
?45 – 3?7 = 55?
If one stacked 73 dice on top of each other on a table, what would be the sum of the numbers that are covered if the top die shows a 3?
A dog’s leash is tied to a corner of a building. There are two tunnels going through the building that the dog can walk through. The lengths of each segment and tunnel are as marked. How long must the dog’s leash be for him to be able to reach every part of the wall of the building?

In the film Die Hard With A Vengeance, the characters John McClane and Zeus Carver open a briefcase only to discover that in doing so they have armed a powerful bomb. It will explode in a matter of minutes unless they can disarm it. Inside the briefcase there is a scale. They have at their disposal two jugs — one holds exactly 5 liters and the other holds exactly 3 liters. To disarm the bomb, they have to fill the 5 liter jug with exactly four liters of water and place it on the scale. A few grams too much or too little will detonate the bomb. The water can be obtained from a nearby fountain.
How can they disarm the bomb?
Make your own set of numbers that has:
a mean of 35, a mode of 30 and a median of 50.
a mean of 40, a median of 40 and a mode of 30.
On the portion of an 8x8 chessboard shown below, the X marks a knight. Knights can move in an “L” shape — 2 squares up or down and 1 left or right, or 2 left or right and 1 up or down. On the board below, the Y’s mark where the knight can move.
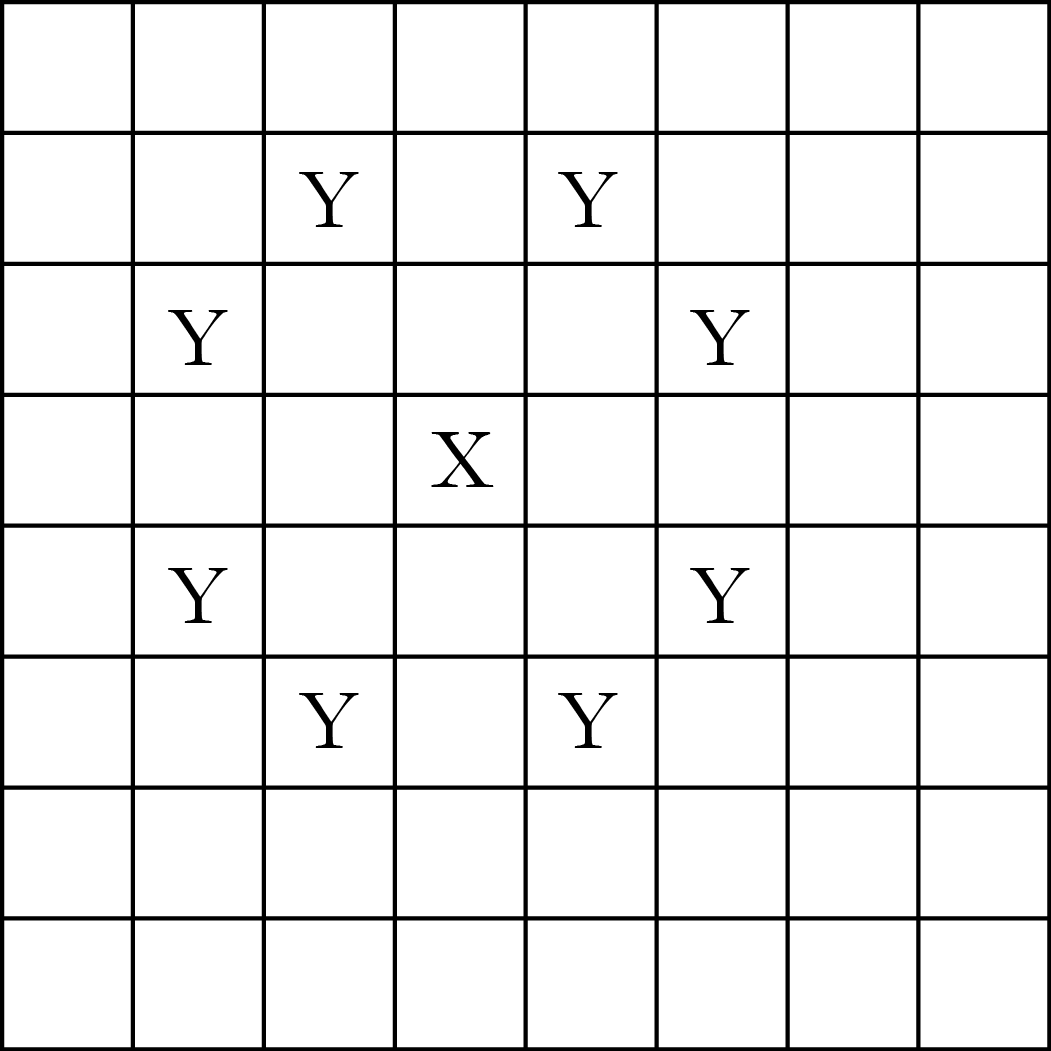
If you can move as many times as you like, can the knight get to any square on the board?
What if the knight moves 3 squares in one direction and 1 in another (instead of 2 and 1)?
What about 1 and 1? Or 3 and 2?
What trends do you notice — under what conditions can the knight get to any square, and when can’t it?
Andie never lies on Monday, Tuesday, Wednesday and Thursday. Leah always tells the truth on Monday, Friday, Saturday and Sunday. On the rest of the days, they may tell the truth, or they may lie. Both say they lied yesterday. What day is today?
You have 46 feet of fence, and you fence in a 120 ${\rm{f}}{{\rm{t}}^2}$ rectangular garden. What are the dimensions of your garden?
From a pile of a large number of pennies, nickels, and dimes, select 21 coins which have a total value of exactly \$1.00. In your selection you must also use at least one coin of each type. There are two answers to this problem — find both.
Peter said: “The day before yesterday I was 10, but I will turn 13 next year.” Is this possible? Explain why or why not. (Math Circles)
${\rm{THIS}} + {\rm{IS}} = {\rm{HARD}}$; what must T stand for, if each letter stands for a different digit?
What is the units digit in ${3^{101}}$?
Arrange the digits 1, 1, 2, 2, 3, 3 as a single six-digit number in which the 1’s are separated by one digit, the 2’s by two digits, and the 3’s by three digits.
Alysha drives from Larchville to Oistin’s Bay at 30 m.p.h. At what speed should she return so that her average speed (total distance traveled / total time taken) for the trip would be 60 m.p.h.?
Let $a + b + c + d + e = a \cdot b \cdot c \cdot d \cdot e$, where $a$, $b$, $c$, $d$ and $e$ are positive integers. Determine how many ordered quintuplets satisfy the equation.
What is the greatest number of points of intersection that
can occur when 2 different circles and 2 different straight
lines are drawn on the same piece of paper?
(from Math Olympiads, George Lenchner)
What is the smallest positive integer that is not prime that is also not divisible by any of the numbers up to 3? Up to 4? Up to 5? Up to 100?