Introduction
Fill in the blanks to continue the pattern you see in this list: $2,\;7,\;6,\;11,\;10,\;15,\;\_\_\,,\;\_\_\,,\,\_\_\,,\;\_\_\,, \ldots $
In mathematics, a sequence is a list of numbers, usually with an identifiable pattern or a connection to real data — for example, the list of expected temperatures for the next ten days, or a sequence listing the profits that a business earned year by year.
The numbers in the sequence are called terms— for example, in the sequence above, 2 is the first term. Sometimes this pattern is very simple: $2,4,6,8…$. Other times it might be harder to spot, like the problem above. Or, it might be an unusual type of pattern — $0,1,0,1,1,0,1,1,1,0,1,1,1,1…$.
Come up with the next two numbers in the sequence $1,3,6,10, \ldots $, and a reason for why they should be the two numbers.
How about the next two numbers in the sequence $2,5,10,13,26,29, \ldots ?$
Make up a sequence that you think will challenge your neighbor — then see if they can find the pattern.
A sequence starts with the numbers 5, 15, 35.
Describe a pattern that this sequence might be following, and give the next three terms according to the pattern.
Now describe a different pattern that the sequence might be following, and give the next three terms according to the new pattern.
The patterns you’ve seen so far have often been related to the differences between terms, such as the patterns in problems 1 and 2. When the pattern in a sequence is simply that the difference is always the same, the sequence is called an arithmetic sequence. For example, $7,9,11,13…$ is one of these.
Some of the sequences below are arithmetic, and some are not. For each sequence, only a few terms are given. Identify whether or not the sequence appears to be arithmetic. Also for each sequence find a pattern and fill in the missing terms.
3, 6, 12, 24, ___, ___, ….
4, 11, 18, ___, ___, ….
9, ___, 17, ___, 25, ….
12, 13, 15, 16, 18, ___, ___,….
47, 43, 39, ___, 31, ___, ___, ….
13, 16, 22, 24, 28, 36, ___, ___, ___....
Development
In a sequence, it’s not only the numbers that matter—the order of the numbers is important too. For instance, sequence “A” — 20, 10, 40, 30, 60, 50, … — follows quite a different pattern from sequence “B” — 10, 20, 30, 40, 50, 60, …. — even though they contain all the same numbers.
In the first sequence, 30 is the 4th term, while in the second sequence, 30 is the 3rd term. To make this type of thing easier to write, we’ll introduce some notation.
In the first sequence, we write “${A_4} = 30$” (pronounced “A sub four” or simply “A four”) to mean that the sequence’s 4th term is 30. Then the first sequence is called $\{ {A_n}\}$ (because it is a set that consists of the terms ${A_1}$, ${A_2}$, ${A_3}$, etc) and the second sequence is called $\{ {B_n}\} $.
Fill in the blanks according to the sequences below.
${A_1}$=_____.
${B_4}$=_____.
${B_{\_\_\_\_}}$= 30.
${A_{\_\_\_\_}}$= 70.
One last piece of notation you’ll need to know is that, in an arithmetic sequence, the constant difference between terms is often called “$d$”. In the sequence below, $d = 2$.
7, 9, 11, 13, . . .
In an arithmetic sequence called $\{ {T_n}\} $, if ${T_1} = 13$, and $d = 3$, then what does ${T_{10}}$ equal? What does ${T_{100}}$ equal?
In an arithmetic sequence, ${T_4} = 8$ and ${T_5} = 11$. Find the first three terms of the sequence.
An arithmetic sequence starts with ${T_1} = 4$, ${T_2} = 9$, … Which term will equal 99?
What might the next two terms be in the sequence 4, 6, 9…? Find several different possible patterns.
Make up five sequences all beginning with 1, 2, but with a different third term. Look at what others in your class came up with, as seeing different patterns can give you ideas for making up some really interesting sequences.
Consider the sequence 5, 10, 6, 12, 8, 16, 12, 24, ...
Find the repeating pattern, and write the next 3 terms.
It looks like all of the numbers after the “5” are even — will the sequence ever produce another odd number? Why or why not?
Consider the three sequences below. Sequences $\{ {D_n}\} $ and $\{ {E_n}\} $ below have some missing information, but you can assume that they are arithmetic.
| $n$ | 1 | 2 | 3 | 4 |
| ${A_n}$ | 12 | 19 | 26 | 33 |
| $n$ | 2 | 4 | 6 | 8 | 10 |
| ${D_n}$ | ? | 41 | ? | 48 | ? |
| $n$ | 9 | 11 | 13 | 15 | 17 |
| ${E_n}$ | ? | 6 | ? | 34 | ? |
Which sequence, $\{ {D_n}\} $ or $\{ {E_n}\} $, has the same value of $d$ as sequence $\{ {A_n}\} $?
Plot the information from the three sequences on a graph (put $n$ on the horizontal axis). Put all three on the same graph. How does what you see fit with your answer to part a?
In your thermometer, the mercury reaches a height of 46 mm when the temperature is 70 degrees Fahrenheit, and a height of 48 mm when the temperature is 73 degrees.
Think about these data as an arithmetic sequence where $n$ is the temperature, and ${H_n}$ is the height at that temperature. Note that “…” is used here to indicate that this table is not showing you values of $n$ and ${H_n}$ where $n$ is less than 70 or greater than 75, but such values still exist.
Fill in the table below:
| $n$ | … | 70 | 71 | 72 | 73 | 74 | 75 | … |
| ${H_n}$ | … | 46 | 48 | … |
What is the value of $d$ for this sequence?
What would the height be if the temperature were at 106 degrees Fahrenheit?
What would the height be if the temperature were at 65 degrees Fahrenheit?
In an arithmetic sequence, the constant difference is sometimes referred to as the rate of change of the sequence. Any idea why it might be so called?
If a sequence has ${T_5} = 40$ but it has a rate of change of $-6$, find ${T_4}$, ${T_6}$, and ${T_{20}}$.
How would you find the value of $d$ for the arithmetic sequence below? (Remember that “…” is used to indicate that there are other value(s) of $n$ and ${T_n}$ that are not listed in this table but certainly exist!) Also write an equation for ${T_b}$ in terms of ${T_a}$, $a$, $b$ and $d$.
| $n$ | … | $a$ | … | $b$ | … |
| ${T_n}$ | … | ${T_a}$ | … | ${T_b}$ | … |
Practice
Another thermometer has a different relationship between height and temperature. For this thermometer, the equation ${H_n} = 0.3n + 17.1$ expresses the height ${H_n}$ (in mm) of the mercury in terms of the temperature $n$, in degrees Fahrenheit.
What’s the height when the temperature is 50 degrees?
If you think of ${H_n}$ as the $n$th term of a sequence, what’s the first term?
What’s the value of $d$ for the sequence $\{ {H_n}\} $?
What would be the temperature if the height of the mercury were 20.7 mm?
What would be the temperature if the height of the mercury were 3 mm?
An arithmetic sequence $\{ {T_n}\} $ has $d = 5.5$, and ${T_{12}} = 48$.
Find ${T_4}$.
For what value of $n$ would ${T_n} = 130.5$?
Each part below gives information about a sequence $\{ {A_n}\} $. In each part, find the value of the unknown in the table for $\{ {B_n}\} $ so that the two sequences have the same rate of change.
(Remember that “…” is used to indicate that there are other value(s) of $n$, ${A_n}$, and ${B_n}$ that are not listed in a table but certainly exist. Thus in the first table of part a, $n$ can be less than 6, can be 7 or 8, and can be greater than 9, even though those values of $n$ aren’t listed explicitly in the table.)
| $n$ | … | 6 | … | 9 | … |
| ${A_n}$ | … | 40 | … | 82 | … |
| $n$ | … | 4 | 5 | … |
| ${B_n}$ | … | $a$ | 48 | … |
| $n$ | … | 16 | … | 22 | … |
| ${A_n}$ | … | 50 | … | 23 | … |
| $n$ | … | 1 | … | 19 | … |
| ${B_n}$ | … | $b$ | … | 40 | … |
| $n$ | … | 9 | … | 31 | … |
| ${A_n}$ | … | 40.5 | … | 71.3 | … |
| $n$ | … | 4 | … | 14 | … |
| ${B_n}$ | … | 4 | … | $c$ | … |
| $n$ | … | 10 | … | 12 | … |
| ${A_n}$ | … | 12 | … | 20 | … |
| $n$ | … | 30 | … | $q$ | … |
| ${B_n}$ | … | 9 | … | 29 | … |
Problems
A sequence $\{ {A_n}\} $ increases by 7 every 5 terms. Starting at the 2009th term, how far would you have to go to increase by a total of 2009?
In an arithmetic sequence…
The first term is 10, and the difference is $d$. In terms of $d$, what is the 20th term? How would you get the $n$th term?
The first term is ${T_1}$, and the difference is $d$. What is the 20th term? How would you get the $n$th term?
Write an equation for the $n$th term, ${T_n}$, in terms of ${T_1}$, $n$ and $d$.
Suppose you have saved \$35 and you also earn \$15 for mowing a lawn.
How many lawns will you have to mow in order to have \$95 saved?
Suppose you wanted to save $380. How many lawns do you have to mow, and how did you get your answer?
How about for \$395?
Let $n$ be the number of lawns you mow, and $M_n$ be the amount of money you have saved after mowing those lawns. Find ${M_1}$, ${M_{10}}$, and ${M_{100}}$.
Write an equation for ${M_n}$ in terms of $n$.
In an arithmetic sequence $\{ {C_n}\} $, you know the following values: ${C_1} = 12$, ${C_3} = 20$, ${C_5} = 28$.
What’s the rate of change?
Does the equation “${C_n} = 12 + 4n$” hold true for the sequence? If yes, explain why it works, and why it will work for every value of $n$. If no, explain why it fails, and fix it to make it work.
The graph below is a data plot for an arithmetic sequence $\{ {T_n}\} $.
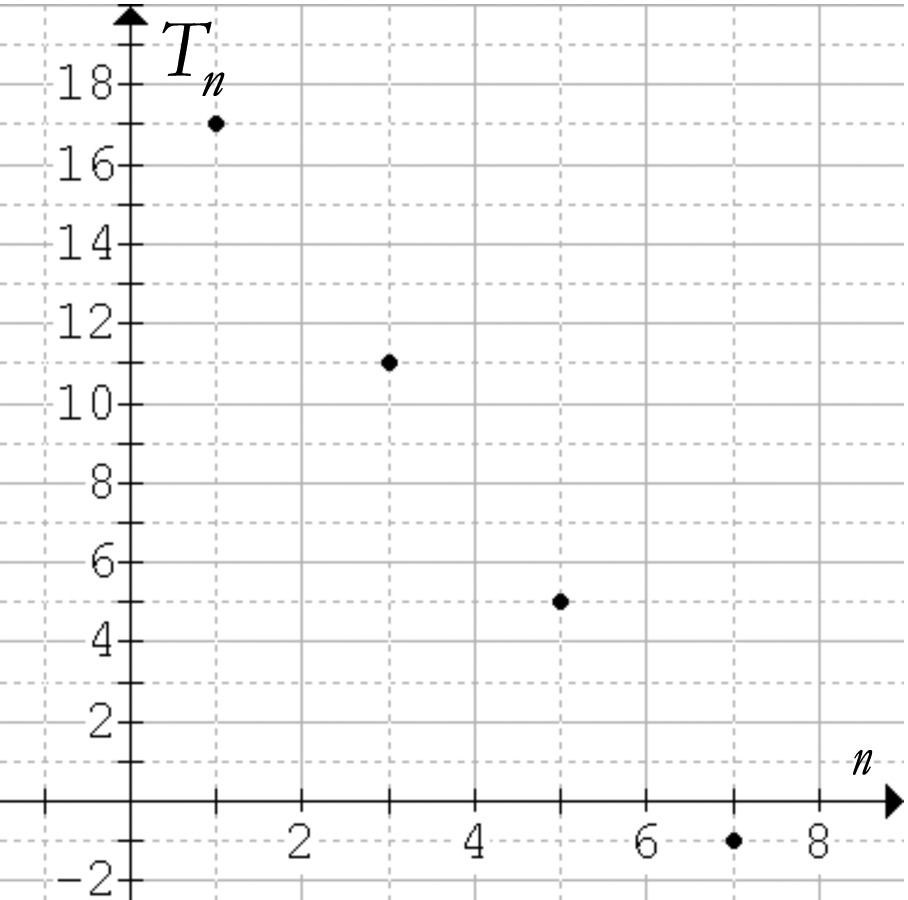
What is the rate of change of $\{ {T_n}\} $?
Write an equation for the value of ${T_n}$ in terms of $n$.
Using the information from sequence ${T_n}$ below, do the following:
| $n$ | 1 | 2 | 3 | 4 | … |
| ${{\rm{G}}_n}$ | 4 | 10 | 16 | 22 | … |
Write an equation for the $n$th term of the arithmetic sequence $\{ {G_n}\} $ above, in terms of $n$ (${G_n} = \ldots $). Be sure to test your equation by plugging in a few values of $n$ to make sure that it works.
Use your equation to determine what ${G_n}$ will be when $n = 40$.
Use your equation to determine what value of $n$ would make ${G_n} = 70$.
Suppose for an arithmetic sequence $\{ {T_n}\} $, ${T_1}=378$ and $d = .001$.
Without using a calculator, roughly estimate what $n$ would have to be so that ${T_n}$ would be about 1 billion.
Now find the answer with a calculator and check that your estimate was a reasonable one.
Write an equation for an arithmetic sequence whose rate of change is 8, and whose fourth term is 60.
Find $x$ if $2, 12, 3x + 10$ is an arithmetic sequence.
Find $x$ if $x, 12, 2x$ is an arithmetic sequence.
When you give $♣(a,b)$ two consecutive terms, $a$ and $b$, of an arithmetic sequence, it gives you the next number in the sequence. Write an equation for $♣(a,b)$.
Create three arithmetic sequences where ${T_9} = 12$ and at least one is a decreasing sequence. Looking at your findings, is there any relationship between ${T_1}$ and the constant difference $d$? Explain.
Do the sequences with the following $n$th terms have any terms in common? ${C_n} = 18 + 3n$ and ${D_n} = 375 - 4n$.
For a sequence $\{ {C_n}\} $, ${C_{10}}=100$, and $d = - 4$.
What is ${C_1}$?
How can this problem help explain why a negative times a negative is a positive?
Find $x$ if the sequence is arithmetic: $7, x, 15$. Do the same for $3, x, 147$. What would be a plausible description of what $x$ actually represents in each case? Would this always work when $x$ is the 2nd of three numbers?
You get a series when you add up the terms of a sequence. For example if you add the first four terms of $3,8,13,18,23,28,…$, you get the series $3 + 8 + 13 + 18$. In the following problems, you’ll develop clever ways to find the sum of a series without actually having to add every term individually — this way, if you have to add up a series that’s 200 terms long, you won’t have to type 200 numbers into your calculator.
Think of ways you could add up the series $1 + 2 + 3 + ... + 59 + 60$ without having to actually add sixty numbers.
Test out your strategies on the following series, then actually add them up number by number to check your answers:
$1 + 2 + 3 + ... + 10$
$1 + 2 + 3 + ... + 15$
How is the series $4 + 8 + 12 + ... + 236 + 240$ related to the problems above? Calculate the sum of this new series.
How about $5 + 8 + 11 + ... + 326 + 329$? Find one way of calculating the series based on your work above, and one way of calculating the series without using your work above. Describe your strategies (and make sure they both give you the same answer!).
Using any strategy, find a quick way to calculate:
$1 + 2 + 3 + 4 + 5 + ... + 299 + 300$
$3 + 4 + 5 + 6 + ... + 89 + 90 + 91$
$6 + 8 + 10 + ... + 140$
$2 + 9 + 16 + ... + 72$
Don’t use a calculator for this problem.
Find $\frac{5}{8} + 3\frac{1}{10}$
Find $7 \div \frac{2}{3}$
Factor $a^2 + 3a - 40$
Factor ${x^2} - 9$
Recall that $|x|$, read $“$absolute value of $x,”$ means to make $x$ positive, so $|3|=3$ and $|-3|=3$. Find $|1-|3-|1-5|||$.
Johnny said that when he added up the 100 terms of the arithmetic series 123 + 129 + 135 + ... + 717 and got about 13000. Mary added up the same series and got about 69000. Halle added them up and got about 42000. One of them is clearly closest to the right answer — figure out which one it must be in under 30 seconds.
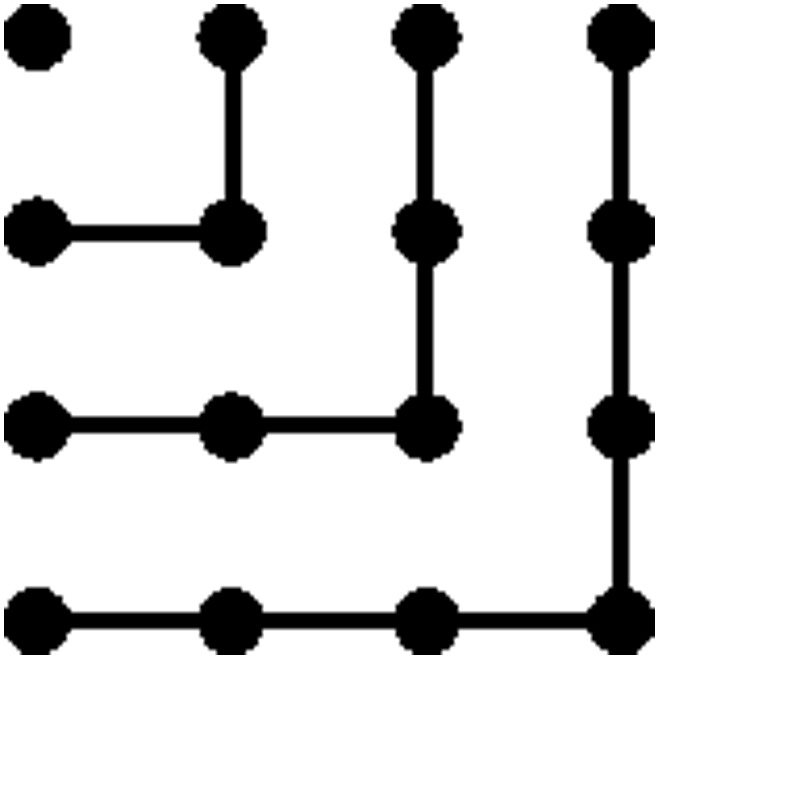
Interpret the diagram below as a series (imagine the number of dots in each piece is the next “term”, and add a few more pieces if necessary to see the pattern). Describe, in words, the terms being added, and describe the answers that you get as you continue adding terms.
Imagine writing out the first twenty counting numbers: $1, 2, 3, ... 18, 19, 20$. Separate the sequence into odds and evens. Find the sum of the odd terms (if you have done problem 44, you’ll know the answer right off). Now consider how the sum of the even numbers compare to the sum of the odd numbers; and then see if you can generate a formula for adding the numbers $1-20$; $1-100$; $1-2n$. Anything familiar about your findings?
You add up the first $n$ terms of an arithmetic sequence: ${T_1}+...+{T_n}$.
Use one of your strategies to give an equation for the answer, in terms of the variables ${T_1}$, ${T_n}$, and $n$.
If $d$ is the difference
of terms in the sequence,
rewrite your equation in terms of ${T_1}$, $d$, and $n$
(without using
An arithmetic sequence has ${T_1} = 7$. You know that $d$ is any integer from 1 to 20. What’s the probability that ${T_n} = 27$ for some $n$?
Exploring in Depth
Compare the following two arithmetic sequences, $\{ {A_n} \}$ and $\{ {B_n}\} $:
| $n$ | 1 | 2 | 3 | … |
| ${A_n}$ | 40 | 44 | 48 | … |
| ${B_n}$ | 2 | 8 | 14 | … |
Will sequence $\{ {B_n} \}$ ever catch up with sequence $\{ {A_n} \}$? How do you know?
Write an equation for $\{ {A_n}\}$, and an equation for $\{ {B_n}\}$. Check that your equations work.
Graph both of your equations on a calculator (“$x$” can stand for “$n$”) and use your graph to determine whether or not $\{ {B_n}\}$ ever catches up with $\{ {A_n}\}$, and when.
Can you confirm that your answer in part c is right, just by using the equations and NOT the graph?
Consider the sequence $\frac{2}{3},\frac{4}{6},\frac{6}{9},\frac{8}{{12}},\frac{{10}}{{15}}, \ldots $.
Find a pattern and the next two terms.
Does the pattern consist of adding $\frac{2}{3}$ to each term?
Look at the ratios of each consecutive pair of terms — what do you find?