When $\because$ is given two numbers it multiplies the first number by 2 and adds to this outcome 3 times the second number.

Write an algebraic rule for $\because$ .

If $a\because 9 = 130$, then what is $a$? Show your work or explain how you arrived at your answer.

The operator $ \Uparrow $ takes two numbers and subtracts the product of them from two times the first number.

Write an algebraic rule for $x \Uparrow y$.

If $x \Uparrow 10 = 46$, then what is $x$? Use algebra to answer this question.

If $10 \Uparrow y = 46$, then what is $y$? Use algebra to answer this question.

Use algebra to determine the value of the unknown that makes the equation true.

$ - 5x + 7 = 29$

$11 - 4y = 6y$

$4 (3y + 1) = 19$

A rule for doing calculations multiplies the first input by 4 then subtracts this quantity from 2 times the second input. This rule uses the symbol ⊕.

Calculate $4⊕2$.

Calculate $-3⊕1$.

Calculate $4⊕(1⊕-2)$.

Write an algebraic rule for $c⊕d$.

Is this rule commutative? Explain.

When you calculate $x⊕y$, you get 26. Write an equation that expresses this fact and solve it for $x$ in terms of $y$. Now, find two different ordered pairs $\left( {x,y} \right)$ that make this equation true.

Create a rule for $\odot$ if it is known that $4 \odot 3 = 7$ and $2 \odot 1 = 5$.

Suppose you know that $x ¥ y = 5y + 2x$. If $x ¥ y = 120$, explain how you can find a value for $y$ that works if $x$ is supposed to be 10. Now, explain how you can find a value for $y$ given any value for $x$.

Solve each of the following equations for the unknown (letter) by using algebra.

$3\left( {x - 5} \right) = 96$

$2 - 2y = 6 + 4y$

$\frac{{b - 3}}{6} = 4$

Writing “$2n$” is a generic way to represent an even number, assuming that $n$ is an integer.

What types of numbers are represented by $3n$? Be specific.

What types of numbers are represented by $4n – 1$?

What’s a generic way of representing a number that is a multiple of 5 but is not a multiple of 10?

Let $c\bigodot d = {c^2} + 3d$.

Calculate 2$\bigodot 4$.

Calculate $3\bigodot (5\bigodot 1)$.

If $c\bigodot d = 36$, give two different pairs of values of $c$ and $d$ that work. (For example, $c=12$ and $d=15$ would be one pair, except for the fact that $12\bigodot 15$ doesn’t actually equal 36!)

If $c\bigodot d = 36$, solve for $d$ in terms of $c$. Then, explain how once could use this result to get thousands (or millions!) of pairs of values of $c$ and $d$ that make $c\bigodot d = 36$.

$4 \bigodot -1$ and $-1\bigodot 4$ both equal 13.
$5 \bigodot -2$ and $-2\bigodot 5$ both equal 19. Can one then say that $\bigodot$ has the commutative property? Explain.

Without using a calculator evaluate each of the following.

5!

$\frac{{5!}}{{4!}}$

$\frac{{100!}}{{99!}}$

$\frac{{100!}}{{98!}}$

A high school coach must decide on the batting order for a softball team of 9 players.

The coach has how many different batting orders from which to choose?

How many different batting orders are possible if the pitcher bats last and the best hitter bats third?

In some states, license plates consist of 3 letters followed by 3 digits — for example, RRK 504. How many distinct (different from each other) license plates are possible?

A school has 400 students. Explain why at least two students must have the same birthday (month and day)?

A school has 677 students. Explain why at least two students must have the same pair of initials. Notice that middle initials are not being included.

A coin is tossed 8 times and the sequence of heads and tails is recorded. How many different sequences are possible?

Suppose you roll two, standard six-sided dice, and suppose one of these dice is green and the other is red. So, one possible roll is a red 1 and a green 3.

How many possible rolls are there?

What are your chances of rolling a sum of seven?

In a math class with 8 boys and 6 girls, the teacher randomly selects two students — one boy and one girl — to put homework problems on the whiteboard. How many different pairs of students can the teacher send to the board?

Without using a calculator evaluate the following.

$\frac{10!15!}{9!16!}$

$\frac{{10! + 9!}}{{9!}}$

Bill has decided that he is going to sit six of his fifteen students in a row toward the front of the class. How many different ways can he do this?

(Continuation of Problem 19) Bill decides to arrange the other 9 students in a row behind the front row of six students. How many different ways can he arrange his 15 students in these two rows?

(Continuation of Problem 20) Bill decides that he’s going to take his six favorite students and always place them in the front row. Is the number of ways that he can arrange his 15 students, now, the same as it was in Problem 19? If so, explain why. If not, provide an arrangement of students that would occur in one problem but not the other.

Suppose we want to form 9-letter words using the letters in the word “fisherman.” Letters cannot be used more than once in each word.

How many 9-letter words are there?

How many 9-letter words are there if each word must begin and end with a vowel?

Suppose the letters of VERMONT are used to form “words.” Letters cannot be repeated in the same word.

How many 7-letter words are there?

How many 6-letter words are there?

How many 5- or 6-letter words are there?

We’re interested in determining the number of 3-digit numbers under certain conditions

How many are there that contain no 7’s?

How many contain at least one 7?

We know that 3! is the solution to the following problem:

How many ways can you stack the three books — Holes, Grendel, and Witches — on a bookshelf?

Draw a tree diagram or table that clearly shows why the solution to the problem is $3 \cdot 2 \cdot 1$. Notice that just because your table or tree diagram has six entries in it doesn’t mean that it clearly illustrates why the solution is $3 \cdot 2 \cdot 1$.

Suppose you roll three, standard, six-sided dice. So one possible roll is 1, 1, and 5.

How many possible rolls are there?

What’s the probability of rolling a sum of 5?

There are 10 students in Bill’s calculus class — 3 girls and 7 boys. Bill arranges 10 desks in a row. How many different ways can the students seat themselves at the 10 desks if

the girls sit at the first three desks on the left?

the girls sit at the third, fourth, and fifth desks?

Suppose students have either 2 initials or 3.

How many different students can have 2 initials without any two of the students having the same two initials? Answer the same question for 3 initials.

What is the smallest number of students the school can have to guarantee that at least two students must have the same initials? Briefly, but clearly, explain how you arrived at your answer.

Suppose you toss a coin 12 times, recording whether you get heads or tails.

How many possible sequences of heads and tails are there?

How many sequences have just one head?

You have 6 classes to do homework in but you only have enough time to complete three of the assignments. How many different ways can you complete the three homework assignments if the order in which you complete them matters? Assume that you don’t go on to another assignment until you’ve completed the one you’re working on at the moment.

You pull two socks out of a drawer containing 3 red socks and 4 green socks. What’s the probability that both socks are red? It will help you think about the problem if you imagine pulling the socks out one at a time.

A soccer team has 16 players on the roster. Only 11 can play on the field at any given time.

How many different “teams” can the coach put on the field? (We are assuming here that even the same 11 players playing different positions is considered a different “team”.)

If only 11 players showed up for next Saturday’s game, now how many different teams can the coach put on the field?

The following Sunday, 11 players showed up, but the coach decided that one of them was the only one able to play goal keeper and another 3 of them could only play defense. Now how many teams can the coach field?

What is the chance that a random 4 digit number that is made only from the digits 1-8 does not have repeated digits?

License plates in Michigan always consist of three letters followed by three single digit (0-9) numbers. Assume repetition of letters is not allowed, but repetition of numbers is.

How many license plates are possible in Michigan?

How many license plates contain only letters taken from the word “Itchy”?

How many license plates contain only vowels and digits that are even prime numbers?

Suppose that you’ve flipped a coin four times and it landed heads each time. What’s the probability that the next time you flip it, it will come up heads?

What’s the probability that, if you toss a coin four times, you’ll get heads exactly twice?

Suppose that there are 60 students in 9th grade, 60 in 10th, 58 in 11th, and 56 in 12th. Each grade elects a president, vice-president, and secretary. How many different student councils are there in each grade?

Use $T_n$ notation to give a formula for each sequence: (${T_n}=…$)

$1,4,7,10…$

the sequence you get by starting at 50 and going down by 4 each time.

$1,1,2,3,5,8,13…$

$1,4,9,16,25…$

$6,18,54,162,486…$

Using a method of your choice (except the method of typing lots of numbers into your calculator), find the sum of each series:

$3+8+13+…+153$

The series with 45 terms, with $T_1=13$ and $d=7$.

The third term in an arithmetic sequence is 20, and the 4th term is 28.

What is the 1st term?

What is the 739th term?

996 is $n$th term in the sequence. What is $n?$

Prove whether 12754 is or is not a term in this sequence.

In an arithmetic sequence ${c_8} = 20$ and ${c_{23}} = - 70$ .

Briefly, but clearly, explain how you can determine the value of ${c_{38}}$ without determining the value of $d$, the constant difference.

Determine the value of $d$.

Determine the value of $c_2$.

Write an equation for $c_n$.

Is there a term in the sequence ${c_n}$ that has the value -432? If so, which term is it? If not, briefly explain why.

The graph of the first 6 terms of a sequence is shown below.

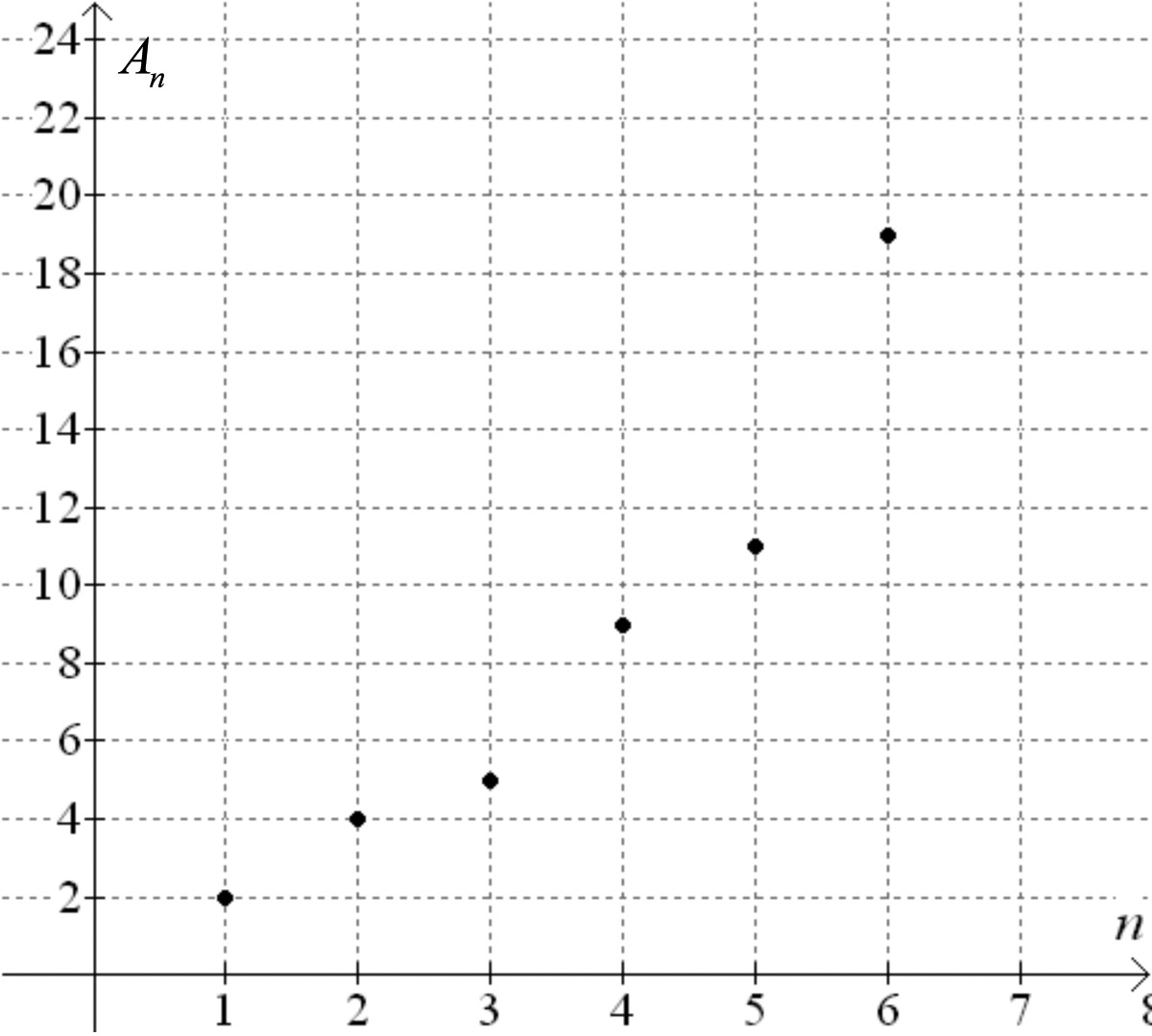
What is the value of ${A_3}$ ?

Is the sequence arithmetic? Explain.

What is the value of ${A_7}$ ? Briefly, but clearly, explain how you arrived at your answer.

In an arithmetic sequence, if $T_{50}=1029$ and $d=8$, find $T_{20}$ and $T_{142}$.

In an arithmetic sequence, if $T_{45} = 79$ and $T_{33}=-77$, find $T_4$ and $T_{50}$.

If $d=12$ and the 25th term of the arithmetic sequence is 148, what is $n$ when ${T_n} =784$?

What is $d$, if ${T_{12}} = - 25$ and ${T_{26}} = - 83$?

An arithmetic sequence goes as follows: $…, 5, X, 11, …, 236, …$.
(Note that “…” means that there are other terms in the sequence that are not being explicitly listed here)

What is $d$, the common difference between terms?

It turns out that 11 is the 14th term of the sequence. What is the 3rd term?

236 is the $n$th term in this sequence. What is $n?$

I’m thinking of a very large number, $Z.$ Tell me how I can determine, in under a minute, if $Z$ is a part of the sequence.