Why are manhole covers circular, instead of square?
You may have heard this “old chestnut” before. (If you have, don’t spoil it for everyone else!) If you haven’t, you may not have any idea how to even begin to think about the problem. Since this is a question about shapes, it may help to draw a picture. Better yet, you could build a model of the situation using, say, a cylindrical oatmeal box and a more rectangular box of cocoa powder. Now that you have a model, play around with it. Look at it from all different angles. Try placing the covers on the different “manholes.” Do you notice anything?
There are many ways to visualize in solving a problem. Sometimes visualizing can be as simple as plotting several points on a graph and interpreting what you see. Visualizing can also involve altering or adding to a given picture to make the problem easier.
How many square units are enclosed by the polygon DANCE below?
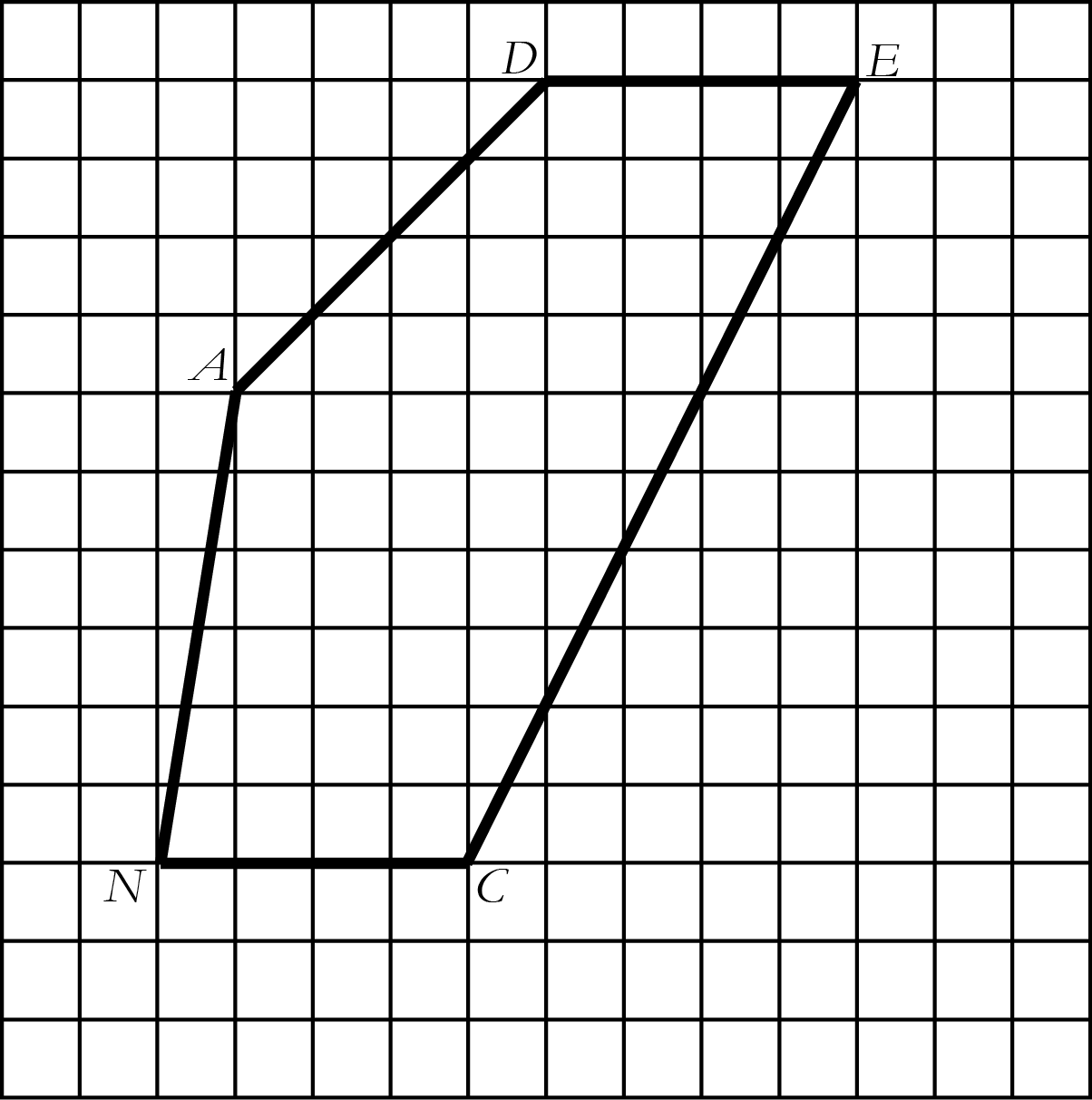
You may have divided the figure in the previous problem into triangles, or even “boxed it in” and found the area of the rectangles you’d created. Either way, the way you reconceived the diagram made it much easier to solve.
In the problems that follow, one of two strategies will help you: 1) Draw or build a model of the situation to make it easier to understand. 2) Alter an existing diagram in some way to gain more information, or simply to help you look at the diagram in a different way.
Below is the usual arrangement of 10 bowling pins, with the “single pin” at the bottom. By moving only 3 of the pins, can you “flip” the arrangement 180 degrees so that the single pin is now at the top?

Alice and Bruno work in a city where the streets are laid out in a grid pattern. City Hall is at (0,0). Alice and Bruno work at (–3,–1) and (3,3) respectively. They wish to find an apartment at a point C such that the sum of the distances each of them has to walk to work is a minimum. Of course, Alice and Bruno can’t walk “as the crow flies” — there are buildings in the way. So what they really mean when they talk about distance is the number of blocks they’d have to walk if they always stay on the sidewalk.
At what place or places could point C be located to satisfy their requirements?
A lattice point is defined as a point with integer coordinates. If $(-3, 5)$ and $(2, 1)$ are two points on a line, find three other lattice points on the same line.
Thomas is watching a train go by. In front of two train cars, there are two train cars. Behind two train cars, there are two train cars. And between two train cars, there are exactly two train cars. What is the minimum number of cars this train could have?
Below is a number line. You can show that 5+3=8 by starting on the number 5, moving to the right three spaces, and landing on the number 8.

Use the number line to show that $5-3=2$.
Use the number line to find $-4+(-5)$.
Use the number line to find $3-(-2)$.
Is it possible to fill a 10” cube with little drawers each 5” by 2.5” by 1”?
How many times might a square and a circle intersect? How about a rectangle and a circle? A rectangle and a square?
There is a theorem in mathematics that states, “The sum of any two sides of a triangle is greater than the third side.” Why would anyone believe that “has to be”?
Lawrence and Erika find a treasure map that tells them where precisely to begin in their search for booty, but then unfortunately it lists 5 directions and says to “follow them in whatever order will get you furthest from your starting position”. Here are the directions:
- 10 Miles North
- 30 Miles East
- $20\sqrt 2 $ Miles Northeast (that is, 45 degrees off from
- North and East)
- $30\sqrt 2 $ Miles Northwest
- $10\sqrt 2 $ Miles Southeast
What order should they take to get as far as possible from their starting position?
You may already be familiar with Venn diagrams, which provide a useful way to organize information. Use a Venn diagram to solve the following problem:
Of 200 children attending a May Day celebration, 74 had their face painted, 125 got a balloon, and 23 had their face painted and got a balloon. How many children did not get their face painted or receive a balloon?
Let’s try a more interesting one. The following data were obtained about 400 people who attended the premiere of “The Hair Witch Project”.
- 150 students bought popcorn.
- 250 students bought a soft drink.
- 200 students bought candy.
- 120 students bought popcorn and a
- soft drink.
- 100 students bought popcorn and candy.
- 130 students bought a soft drink
- and candy.
- 80 students bought popcorn, a soft
- drink, and candy.
How many students did not buy any of the three items?
Let’s look at the exciting, dramatic adventures of a bobsledder.
A bobsledder starts a race by going 100 miles South. He then goes 100 miles East, and then 100 miles North to complete the race. Amazingly, the end of the race is at the exact same place as the start of the race! How is this possible?
Is the starting place you came up with in part a the only possible correct answer? Explain why or why not.
You have an 8.5 by 11 inch piece of paper (standard size). Fold the paper in half so the top edge and the bottom edge meet, and then unfold it. Now you cut it along the diagonal of the entire sheet of paper, and keep one of the triangular pieces.
What’s the area of the piece of the triangle that’s above the fold? What’s the area of the piece below the fold?
Suppose you have three bricks and a ruler, but no calculator.
Find a way to measure the longest diagonal of the brick—the one that goes “inside” the brick to connect opposite corners. (Since you have no calculator, you won’t be able to use the Pythagorean Theorem.)
Now, suppose you stacked three bricks on top of each other. Can you find a way to measure the longest diagonal of the block this forms? (Still no calculator!)
It is easy to cut a cylindrical piece of cheese into 4 identical pieces with 2 straight cuts, and into 6 identical pieces with 3 straight cuts. One day, Mr. Trump decides to cut a cylindrical piece of cheese into 8 identical pieces, and unsurprisingly, it takes him 4 cuts.
Rosie, his nemesis, claims she could have done it in only 3 cuts! Was she telling the truth, or is she just trying to get Trump’s comb-over to stand on end?
Can you determine a way to divide a square into 7 smaller squares that are not all the same size? How about 6 smaller squares?
A power of two is a number like 4, which is $2^2$, or 64,
which is $2^6$, or any other number that can be written
in the form
Five kids are playing “eeny-meeny-miney-moe.” They play the game by going around a circle and pointing at each kid in turn on each beat of the chant. The chant has sixteen beats. The kid they point to on the last syllable of the chant is “out.”
If kid #1 is the kid they point to first, which kid will be out?
What about a game with fifteen syllables and four kids?
What about a game with twenty syllables and three kids?
What about a game with a hundred syllables and seven kids?
In middle school, you probably learned how to represent fractions as “pieces of pie.” Below are representations of the fractions 1/3 and 2/5.

Draw “pieces of pie” to illustrate that $\frac{1}{3} + \frac{1}{3} = \frac{2}{3}$.
Draw “pieces of pie” to illustrate that $\frac{1}{2} + \frac{1}{4} = \frac{3}{4}$.
Draw “pieces of pie” to illustrate that $\frac{1}{2} + \frac{1}{3} = \frac{5}{6}$. (First think about how you would represent “finding a common denominator.”)
A store manager wants to decide whether to break down boxes measuring $3' \times 4' \times 4'$ or use them for shipping ski equipment. Can a set of $6'$ skis fit into those boxes? Why?
A circle of radius 1 rolls inside a circle of radius 2. Describe the path traced by a piece of gum stuck to the rim of the inner wheel. (Make a model!)
Shelly buys a new fishing rod and then prepares to take the bus home. When she tries to get on the bus, the driver says, “no way can you take that fishing rod on the bus — it’s five feet long, and we don’t allow any objects longer than four feet on this bus! Without the bus, Shelly is stranded, so she goes back to the store to return the rod. However, the clerk tells her that the rod is nonreturnable. In a flash of insight, Shelly comes up with a plan. She asks the clerk for a specific object, which he gives her, and sure enough, she is allowed on the next bus. Shelly’s plan didn’t involve breaking any laws, and it didn’t involve changing the rod in any way, certainly not by cutting or bending it, either! What was her plan?
The cylinder below has a spiral drawn on it. The spiral loops around the cylinder exactly four times.

You measure the cylinder and find that it is 10 inches tall and 4 inches across. Then, to measure the length of the spiral, you cut up along the left side of the cylinder (imagine that it’s hollow, like the cardboard from a roll of toilet paper). Draw what the spiral would look like once you cut open the cylinder and flattened it into a rectangle — you can try this with an actual toilet paper roll or something similar.
How tall would the rectangle be?
How wide?
Use this information and your drawing to figure out the total length of the spiral.