The diagram below shows a rectangle (not a square) that has been cut into 9 squares, no two being the same size. The smallest square is 3 cm by 3 cm. Find the sizes of the other squares.
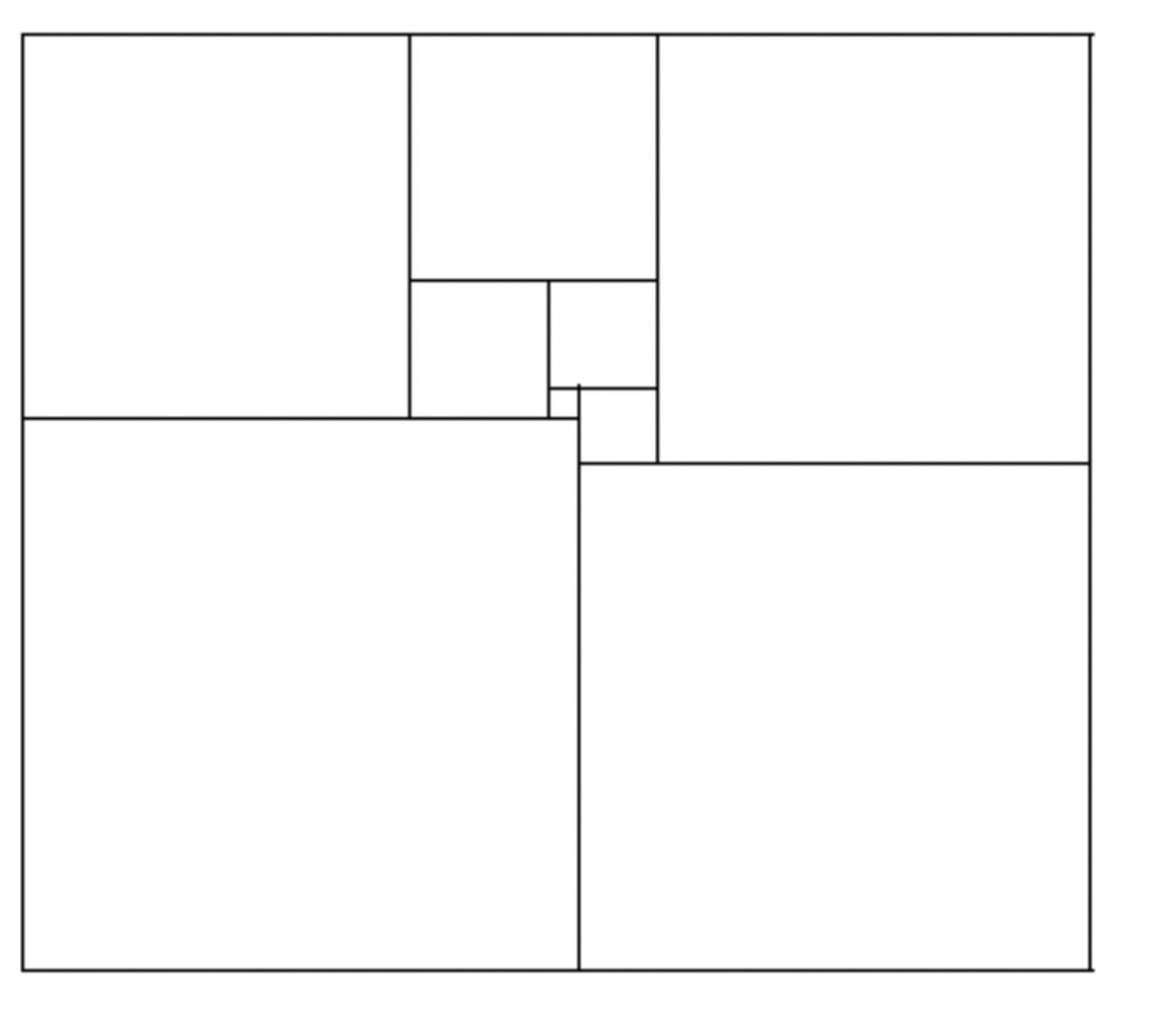
In trying to solve problem 1, some of you might have first tried a little tinkering. The diagram does suggest that a side of the second smallest square might be somewhere between 6 and 9, and so you might have tried some or all of the integers 6 through 9. As it turns out, not only do none of these integers work, but after trying any one of the numbers it might not be at all clear to you whether it would be too high or too low. So refining the process to get at the answer might prove to be a bit challenging.
On the other hand, some of you algebra lovers might have bypassed that wonderful play and jumped right into some symbolic representation of the length of the side. If you haven’t already done so, give algebra a try.
Representing the length of a side of the second smallest square (or some other square) by $x$:
Work around the diagram, and find an expression involving $x$ for the length of the left side of the rectangle.
Find an expression involving $x$, different from that in part a, for the length of the right side of the rectangle.
By equating the expressions in parts a and b, solve the resulting equation for $x$.
Now find the sizes of all the squares.
Even though you might have been able to discover the answer by tinkering, you might also agree that the algebra approach was somewhat more efficient, despite the fact that it was certainly not a walk in the park and required a great deal of care and manipulation. Further, the algebra not only provided a solution that you could be sure of, but also provides a way for you to communicate your solution in a clear and convincing manner.
Of course algebra is not a panacea. It is not the best approach for all such problems, and even when it is the best approach one still has to make decisions about which of the unknown properties should be replaced by variables. And even after you have made these decisions, you may realize that the equation you have written requires very difficult algebra to solve, so much so that you need to learn new skills to have any hope of solving it.
In addition to its efficiency, security and its ability to communicate succinctly and cogently, an algebraic approach can provide you with a deeper understanding of the problem. In problem 2, for example, you might have been able to discover the relationship between the size of the smallest square and the sizes of the other squares, allowing you to see the solution for a starting square of any size. Using algebra can also allow you to investigate the possibility of multiple correct answers, something that a more tinkering approach is less likely to reveal.
Take a look at another problem.
What happens when you take four consecutive numbers, add them all up, add 10, and divide your answer by 4? Try it four or five times to test your observation.
But can you be really sure that what you think happens in problem 3 always happens no matter what four numbers your start out with? You can of course produce a complicated verbal argument but an algebraic argument would be far more convincing.
Prove the result in problem 3.
The Climate Change Committee at Park (CCCP) is trying to raise $\$10000$ to put towards restoring the eroding banks of the stream. They happily announced that 25% of what they’ve already collected is equal to $\tfrac{2}{3}$ of the amount still needed. How much has the CCCP already collected?
Try this coin trick out on your friends. Get \$2.85 in change, and keep it in your pocket. Now, find a friend who’s got some change in her pocket. Have your friend hold the change from her pocket. For effect, you can have her jingle the change, and pretend you’re listening really carefully. Then, tell your friend: “I can tell, just by listening, how your amount of change compares to my amount. I think that I have exactly what you have... plus fifty cents... and then enough left over to make your change equal \$2.35.”
As long as you have more change than your friend, this trick will ALWAYS work! Why?
Paul places 7 bags of marbles onto a table. The second bag has 2 more marbles than the first bag. The third bag has 4 more marbles than the second bag. The fourth bag has 6 more marbles than the third bag and so on. The total number of marbles in all seven bags is 231. How many marbles are in each of the bags?
Boxes and spheres: In the following diagram, there are two kinds of items--boxes and spheres. Boxes all weigh the same, and spheres all weigh the same.
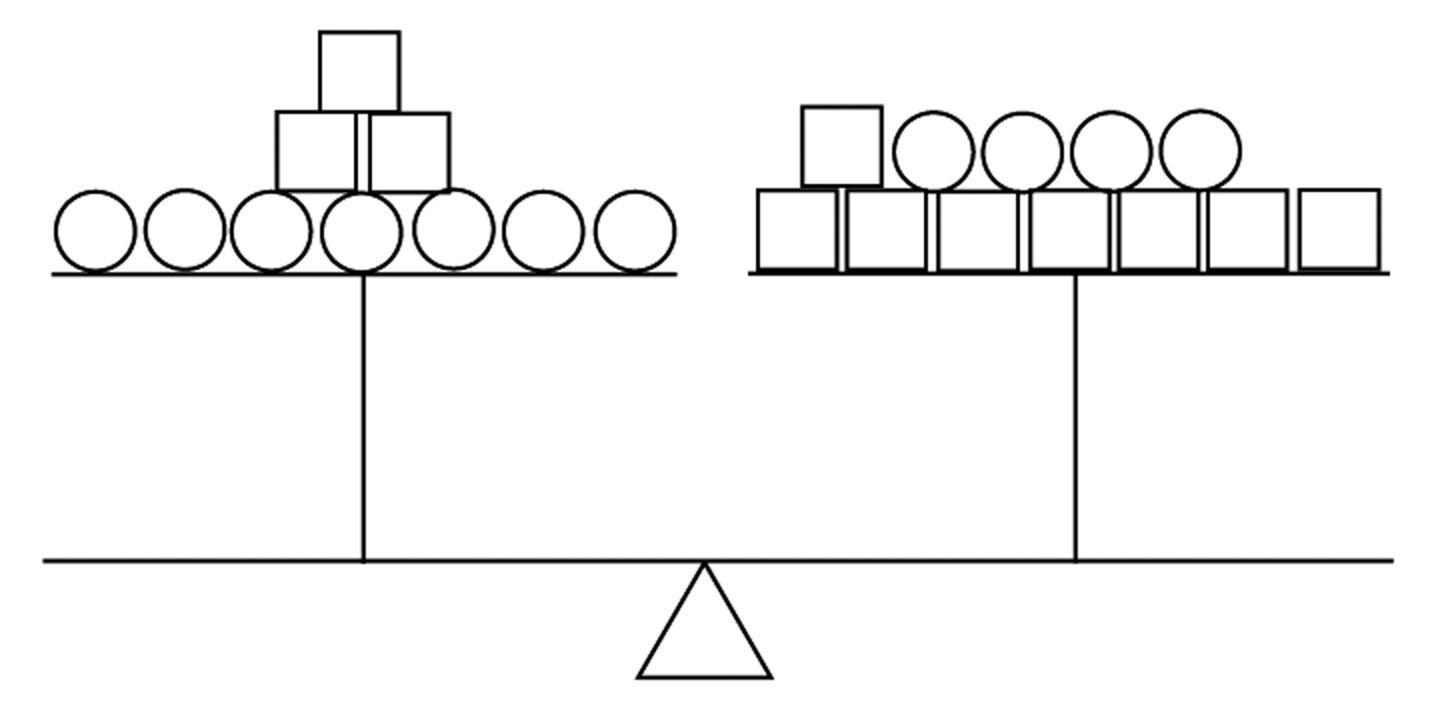
If spheres weigh 2 pounds each, how much do boxes weigh?
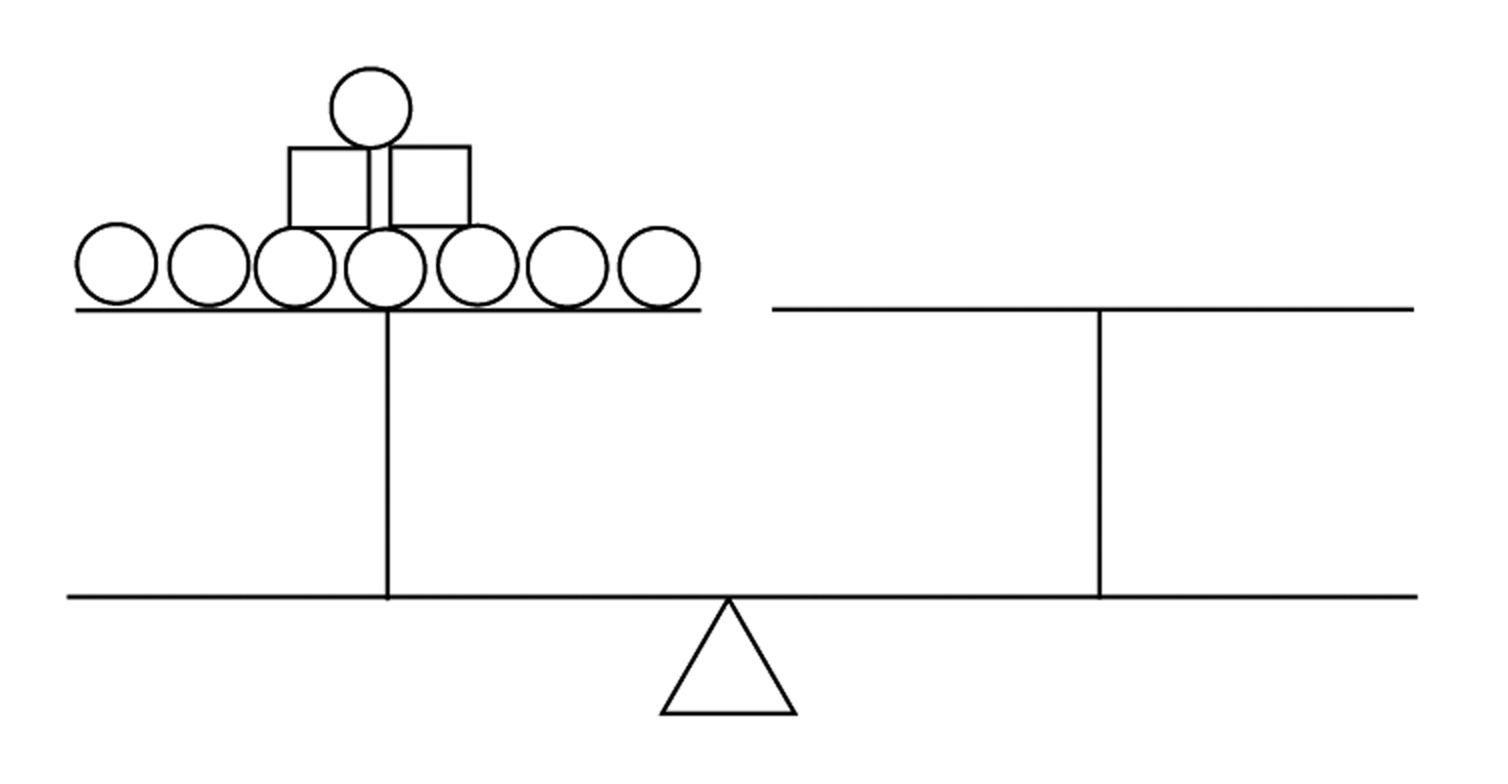
Now suppose the spheres don’t necessarily weigh 2 pounds. Find a way to add boxes and spheres to the right side scale below so that the scale will balance. Your answer must be something other than “8 spheres and 2 boxes.”
Abigail’s age is 12 years plus 2/3 of her age. How old is she?
Betty has half the number of bedbugs as Buford, and four times the number of bedbugs as Bernice. Among the three of them, they have 2600 bedbugs. How many bedbugs does Betty have?
Bristlecone pines are high-altitude trees famous for their longevity. You learn that one pine started growing 2,436 years before a smaller pine growing on the other side of the mountain. 50 years ago, the larger pine was exactly four times older than the smaller pine. What are the ages of the two pines?
(From braingle.com) A magical dragon has three heads and three tails. The knight sent to slay the dragon has an especially difficult task. If any one of the dragon’s heads is chopped off, a new head grows. If a tail is chopped off, two new tails grow. If the knight chops of two tails at once, one new head grows. But if he chops off two heads at once, nothing grows.
Any stroke of the knight’s sword will chop off either one or two heads, or one or two tails. It will never chop off a combination of heads and tails.
What is the smallest number of strokes required chop off all heads and tails of the dragon, thus killing it?
Take any three consecutive integers and add them together. If you repeat this a few times you will notice something interesting about the sum. What is it? Prove that this will always be the case.
Imagine taking a number and adding its reciprocal. (Note: Once you have a symbolic representation for this procedure, using the graphing feature on your calculator could be very useful in providing evidence for your answers below.)
Do you think there would be numbers for which the answer would be 5? How many?
Do you think there would be numbers for which the answer would be 2? How many?
Do you think there would be numbers for which the answer would be 1? How many?
The Park School Ninth Grade class decided to sponsor a fundraising trip to Owings Mills to see the spectacular mall. They arranged for a 60-passenger bus costing \$360. If the bus is filled, they will charge \$9 per person. If the bus is not filled, for each empty seat, they will increase the price per person by \$1. What is the maximum profit the club can make from this fundraiser? (For this one you might want to graph on your calculator as well.)
Last year three fifths of the mathematics society were girls, but this year the number of boys doubled and six of the girls dropped out. There are now twice as many boys in the society as there are girls. How many members were in the society last year?
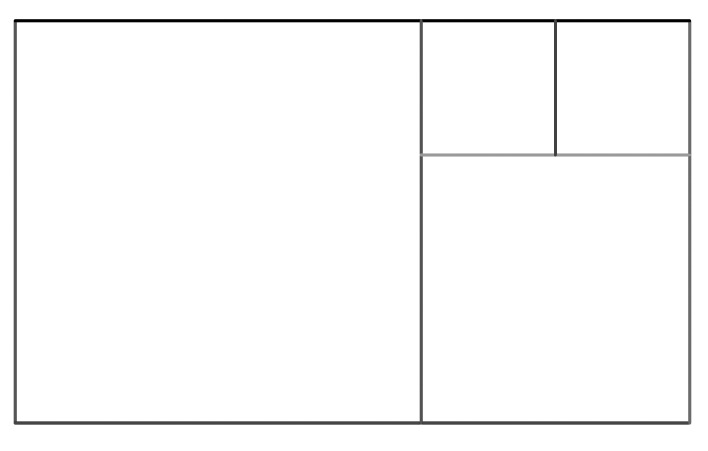
In the figure below, a rectangle is divided into four squares. The width (bottom side) of the rectangle is 35 cm. Find the perimeter of the rectangle.
Find five consecutive integers whose sum is 2874.
How many numbers have the following property? When three is added to the number and the sum squared, the result is the same as when 9 is added to the square of the number?
Pick a number, add four, multiply by six, divide by three, then subtract eight.
What always happens? Once you figure it out, try this game on a parent or friend and see if you can “read their mind” — guess their original number when they tell you their final number.
Why does this trick work?
Make up your own trick like this, and test it out on a parent or friend.
Ebay drove to school yesterday at 30 miles per hour and returned home at 40 miles per hour. In order to find his average speed for the entire trip, Ebay was busy with an internet search for the distance from his home to Park, when Paul happened along. “No need to do the search — the distance does not matter.” Is Paul correct?
Find the diameter of a circle whose circumference is $Z$ cm and whose area is $Z\,\mathrm{cm}^2$. Is there more than one possible answer?
This is a translation of the inscription on the tomb of Diophantus, a Greek mathematician who is famous for studying number theory. Can you figure out how old Diophantus was when he died?
Here lies Diophantus,’ the wonder behold. Through art algebraic, the stone tells how old: God gave him his boyhood one-sixth of his life, One twelfth more as youth while whiskers grew rife; And then yet one-seventh ere marriage begun; In five years there came a bouncing new son. Alas, the dear child of master and sage, after attaining half the measure of his father’s life chill fate took him. After consoling his fate by the science of numbers for four years, he ended his life.
Weisstein, Eric W. “Diophantus’s Riddle.” From MathWorld--A Wolfram Web Resource.
Accept the dubious scientific fact that potatoes are 99%
water and 1% potatoey-stuff. You leave 100 pounds of potatoes
in the sun so that they dry out. After
a while, the potatoes have dried out enough so that they are
now 98% water. How much does the pile of potatoes weigh
now?
Copyright cartalk.com
Zack runs a lawn mowing business. He’s hired eleven employees to mow lawns for him, while he runs the office and does marketing and hiring. In order to make money, Zack takes a 10% cut of the money each employee earns. One day, the employees realize that, while they only keep 90% of what they earn, Zack gets a total of 110% of a typical employee’s salary. They decide to strike unless Zack will agree to take a smaller percent cut that will result in Zack’s earnings being equal to everyone else’s. To appease his employees, what percent cut should Zack now take from their earnings?
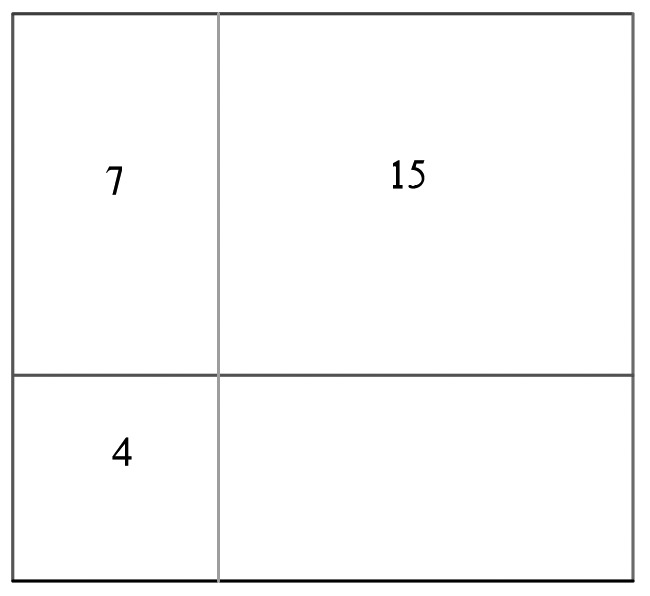
A rectangle in the diagram below is divided into four rectangles. The areas of three of the rectangles are shown. What is the area of the fourth rectangle? (Think carefully about which length you should represent by a variable.)
Roger has 6 times as many dimes as nickels and 3 times as many pennies as nickels. If he has \$17, how many coins of each kind does he have?
The Yaks club has 500 members. They’ve just announced a
charity fundraiser with the following ticket prices: old
members pay \$20, but new members get a special rate of \$14.
All of the new members decide to come, but only 70% of the
old members are coming. How much money will the Yaks make in
ticket sales?
Adapted from www.cartalk.com
The Yaks club decides to throw another charity fundraiser — this time with the following ticket prices: old members pay \$20, but new members get a special rate of \$13. All of the old members decide to come, but only 71% of the new members are coming. This time, how much money will the Yaks make in ticket sales?
When Laila finally took her trigonometry test, her score of 94% raised the average class score from 79 to 80. How many students are in Laila’s math class?
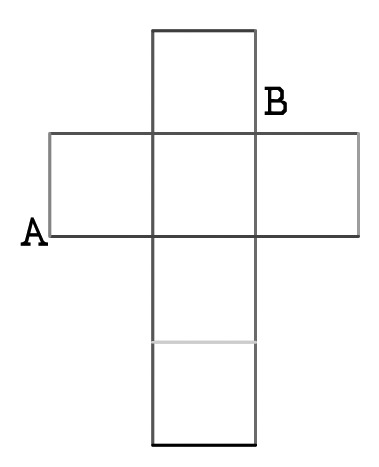
The figure below is made of six squares. AB is 6 cm. Find the area of the figure.