Introduction
Your 8-year-old neighbor Joe has set up a lemonade stand. To help him out you agree to buy a cup, but are surprised to find that he charges for the cup as well as the lemonade. His price is 30 cents for the cup itself, and then 80 cents per cupful of lemonade.
How much would Joe charge for someone who bought the cup and then drank 5 cupfuls?
Beth spends \$5.90 at the lemonade stand. How much lemonade did she drink?
You realize that you have less than a dollar’s worth of change, so you can’t buy a full cup. How much do you think Joe should charge you for getting a cup that’s half full of lemonade? (Remember you still need to pay for the cup!)
How much should Joe charge for a cup that’s 90% full?
Write an equation for $P$, the price of your purchase, in terms of $L$, the amount of lemonade that you buy, measured in cupfuls (which might not be a whole number).
Linear equations are used to model the same kinds of patterns that you see in arithmetic sequences — patterns where the data show a steady rate of change. One benefit of a linear equation is that you’re no longer restricted to whole numbers — you can find the price of 3.42 cupfuls of lemonade — whereas with a sequence, you could only have the price of 1 cup, the price of 2 cups, the price of 3 cups, and so on.
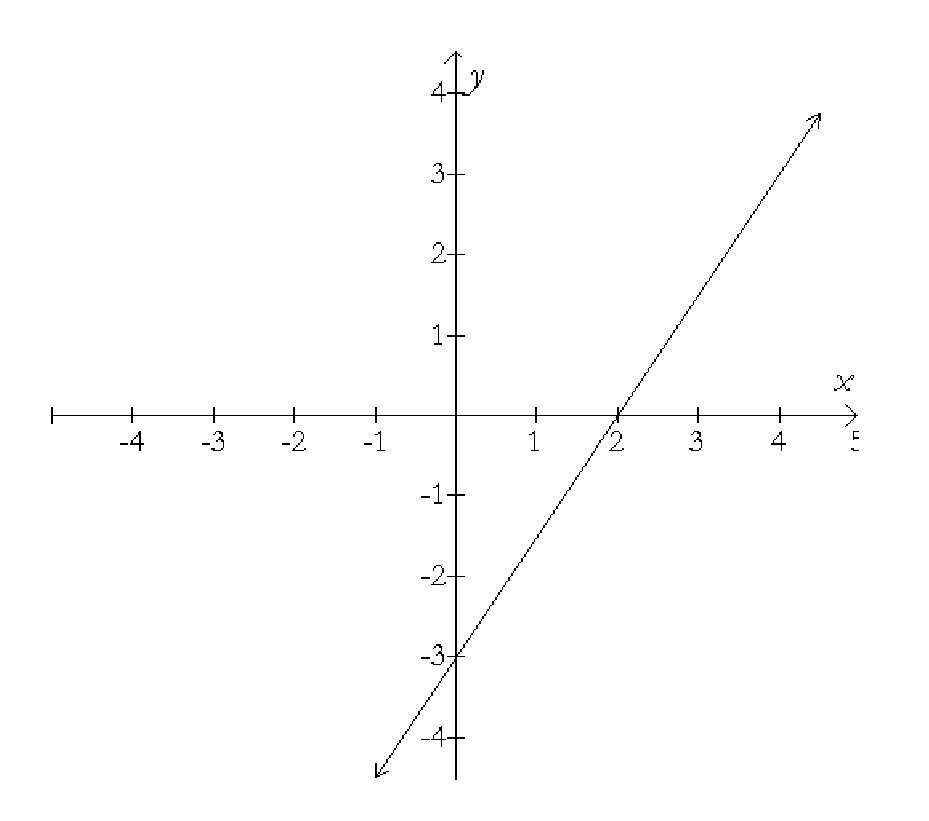
When you graph a linear equation, one of the most critical pieces of information you see on the graph is the slope of the line. Recall that slope is a measure of the steepness of a line, and is calculated by finding “rise over run” — for example, the line below “rises” 6 units every time it “runs” 4 units, so its slope is 6 over 4, or 1.5.
Development
This lesson underscores the advantages of using multiple points of view — looking at problems or situations from several perspectives. Specifically we will see how shifting among sequences, graphs and algebraic equations can make a difficult problem quite accessible.
In an arithmetic sequence, ${T_1} = 10$, ${T_2} = 14$, ${T_3} = 18$, ${T_4} = $…
Graph the points of this arithmetic sequence on a coordinate plane (use $x$ to stand for $n$, and $y$ to stand for ${T_n}$).
Draw the line that goes through the points you drew.
What is the rate of change of the sequence? In what way is this rate related to the line?
Write an equation of the line — an equation showing the relationship between $x$ and $y$.
The points $\left( {a,30} \right)$ and $\left( {b,60} \right)$ are on the line. Use your equation in part d to find $a$ and $b$.
Two terms of an arithmetic sequence are ${B_3} = 40$ and ${B_{10}} = 68$.
If you graphed the points of the sequence, and then drew the line that goes through these two points, what would be the slope of the line you drew?
The points $\left( {12,a} \right)$, $(100, b)$, and $\left( {c,89} \right)$ are on the line described in part a. Find $a$, $b$, and $c$.
Write an equation for the line. Test it by plugging in 3 and 10 for $x$ to make sure it works.
A line contains the points (12,9) and (3,10). Draw the line on a set of axes, then find:
The slope of the line.
An equation for the line.
The value of $x$ that will make $y$ equal 12.
The values of a sequence are represented by the equation $y = 4x - 9$. (Here $x$ is playing the role of $n$, and $y$ is playing the role of ${T_n}$).
Find the first term of the sequence ($x = 1$).
Find the rate of change of the sequence.
What’s the value of the 7th term of the sequence?
Which term of the sequence has a value of 31? (If you got 115, re-read the question!) Figure out a way to answer this question without writing out all the terms of the sequence until you get 31.
Will the number 111 ever appear in the sequence? If yes, when? If no, why not?
Will the number 173 ever appear in the sequence? If yes, when? If no, why not?
A linear equation has the following graph:
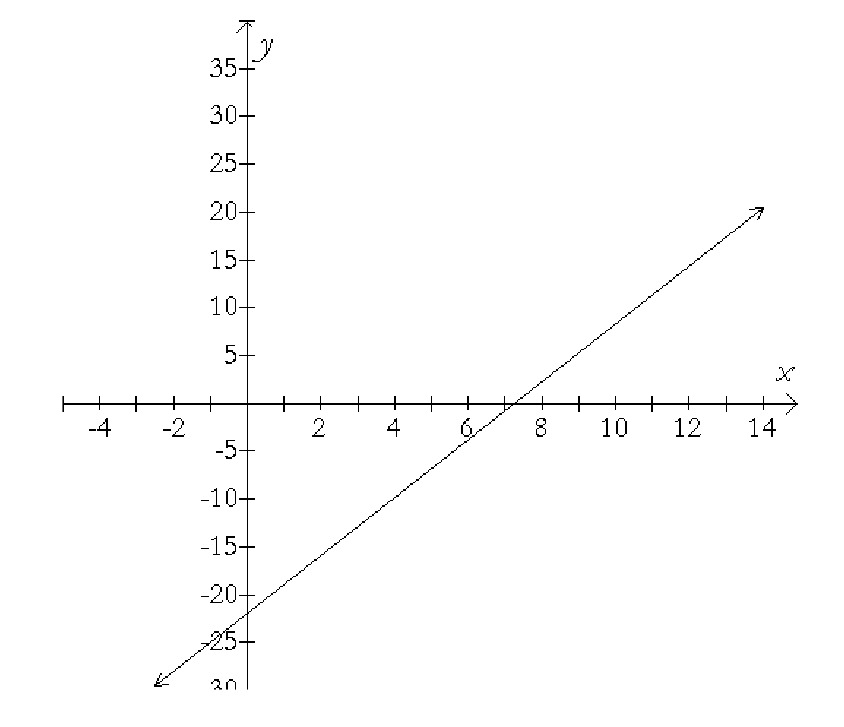
Use the graph to estimate the value of $y$ when $x$ is 4, and when $x$ is 10.
Estimate the slope of the line.
Estimate the value of $x$ for which $y$ would equal 100.
Do you think the point $(40,98)$ would be on the line? How about $(50,158)$? Be precise in your explanation.
You have an aquarium with fish and snails in it. There’s a limited amount of oxygen in the tank and so the two species are in competition for the oxygen. The relationship between $x$, the number of fish living in the aquarium, and $y$, the number of snails living in the aquarium, is linear. The graph of the line is below:
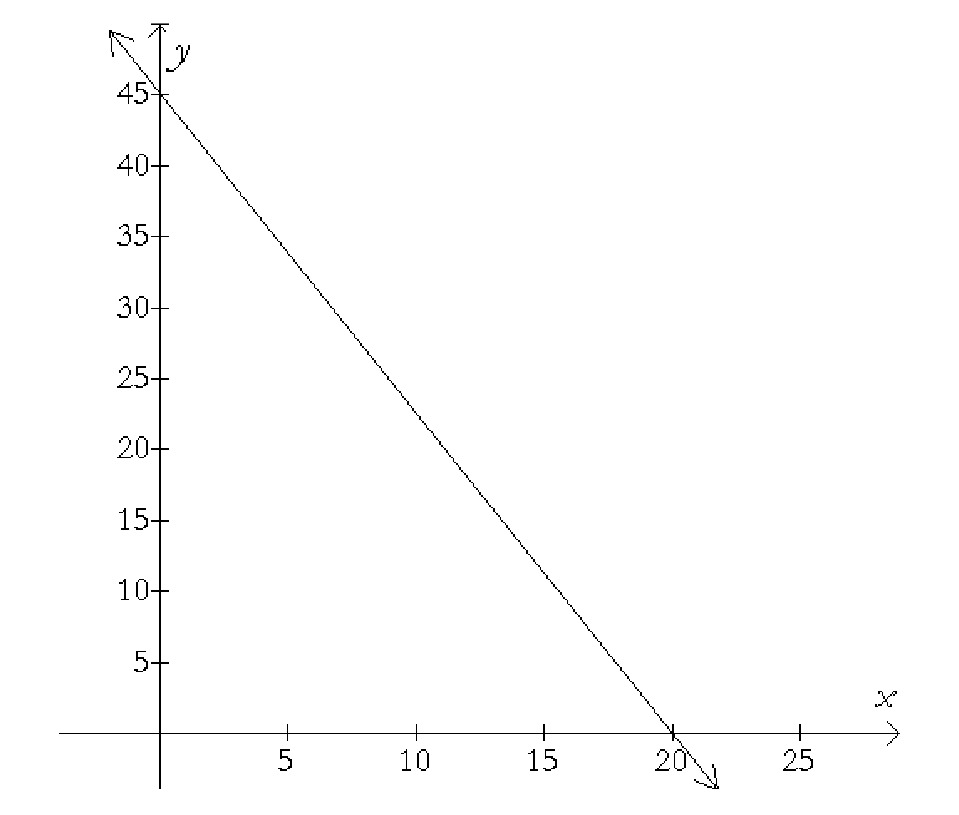
What’s the value of the $y$-intercept of this line, and what does it mean in the context of the problem situation? (Recall that the $y$-intercept of the graph is the point where the graph crosses the $y$-axis.)
What’s the value of the $x$-intercept of this line, and what does it mean in the context of the problem situation? (Recall that the $x$-intercept of the graph is the point where the graph crosses the $x$-axis.)
It is customary to describe the $x$-and $y$-intercepts using only the $x$- or $y$-coordinate. For example, a line with $y$-intercept (0, 16) is said to have a $y$-intercept of 16.
Practice
You write an important lab report, and want to have it printed professionally. The print shop tells you that in addition to paying a rate of 11 cents per page, you’ll also have to pay 75 cents for the cover and binding.
If your lab report is 20 pages long, how much will it cost to get it printed?
You change your writing to a smaller font to make it cheaper – now the report is only 17 pages long. How much will it cost now?
You need to make the report even shorter, because you want it to cost at most \$2.25. How short does it need to be?
Write an equation to reflect the information. Use $x$ to represent the number of pages, and use $y$ to represent the price you pay.
A line has a $y$-intercept of 16 and a slope of -3. Find:
An equation for the line.
The $x$-intercept of that line.
Find $d$: $\left( {12,d} \right)$ is on the line.
Find $w$: $\left( {w,3} \right)$ is on the line.
Looking at two lines, you see that the point $\left( {3,3} \right)$ is on both lines.
The $x$-intercept of the first line is 12. Find its slope.
The slope of the second line is $\tfrac{1}{4}$. Find its $x$-and $y$-intercepts.
Problems
After considering the print shop from problem 8, you decide that you’d rather have your report printed at a different store. The new store has the same pricing system — a charge for the covers and binding, and a charge per page — but you forgot to ask about the specific rates.
You do remember being told that a 15-page report would cost \$1.78 to print, and a 19-page report would cost \$1.98.
How much would a 21-page report cost to print?
What is the rate they charge, per page?
What would it cost to make an “empty book” — just the covers, no pages inside?
For \$50, what’s the longest report you could print?
An arithmetic sequence has terms ${A_4} = 40$ and ${A_{14}} = 14$.
Write an equation for a line that would contain these two points.
What’s the $x$-intercept of this line? The $y$-intercept?
What’s the first negative term in the sequence? Explain how your answer relates to part b.
On your line, for what value of $x$ will $y$ equal 1? For what value of $x$ will $y$ equal 20?
Find out whether there is a term ${A_n}$ of the sequence that equals each of the following numbers: 30.4, 21.8, and 79.
You are driving on a road that travels up from a valley. Your elevation (your height “above sea level”) increases steadily over time — in other words, its rate of increase is always the same.
40 minutes after you start driving, you are at an elevation of 700 feet above sea level. After 10 more minutes, you are 735 feet above sea level.
What’s the rate of increase of your elevation?
What was your elevation level when you started driving?
Write an equation for $E$, your elevation, in terms of $t$, the time you’ve been driving.
Use your equation to determine when you’ll be at an elevation of 875 feet, and when you’ll be at an elevation of 900 feet.
An internet café charges $\$15$ an hour for internet access, and $\$9.50$ per pound for its famous chocolate-covered coffee beans.
If you spent $H$ hours online and ate 3 pounds of beans, spending a total of $\$141$, what is $H$?
You spend $H$ hours online and eat $P$ pounds of the beans. In total, you spend $\$40$. Write an equation about this situation to relate $H$ and $P$.
The symbols you worked with in the last chapter were examples of mathematical functions. A function is something that takes an input and somehow uses that to produce an output. Consider the simple linear function ∆, which takes a number $t$, multiplies it by 2, and adds the result to 7.
Write an equation for ∆. (∆($t$)=…)
Sketch a graph of the outputs vs. the inputs of the function ∆. You will first have to decide how to label each axis, of course.
A line goes through $(2,20)$ and has slope 3502. It also goes through the point $(1.5,a)$ and $(200,b)$. In your head, determine reasonable estimates for $a$ and $b$.
If $y = \sqrt 2 \,x - \sqrt 2 $ and $x$ is an integer, can $y$ be an integer other than 0? If so, which one(s)? If not, explain why not.
To make a perfect peanut butter and jelly sandwich, you need to have exactly 1.2 ounces of peanut butter per ounce of jelly you start with, then add an extra ounce of jelly.
If you use 3 ounces of jelly, how much peanut butter should you use?
Now what if you use 3 ounces of peanut butter — how much jelly do you need?
Do you always have more jelly than peanut butter? If yes, why? If no, give an example of a perfect PB&J sandwich that has more peanut butter than jelly.
Write an equation showing the relationship between $j$(amount of jelly) and $p$(amount of peanut butter). Then graph this equation with $p$ on the horizontal axis.
Which point on your graph represents a sandwich with no peanut butter, just jelly?
Is there a point on your graph that represents a sandwich with no jelly, just peanut butter? How much peanut butter will you need then?
In each case find $k$ to make the statement true:
The point $\left( {3,9} \right)$ is on the line $y = 2x + k$.
The point $\left( {3,9} \right)$ is on the line $y = kx - 3$.
The slope of the line containing $\left( {3,9} \right)$ and $\left( {k,49} \right)$ is 2.5.
The line containing $\left( {3,9} \right)$ and $\left( {5,k} \right)$ has a $y$-intercept of 24.
You are comparing two printer companies, PrintCorp and InkCorp, to print your next big report. PrintCorp charges \$.80 for the cover and binding, and 8 cents per page. InkCorp, who has a similar pricing system, tells you that \$10 will buy you a 223-page book, and \$20 will buy you a 473-page book.
For each company, write an equation for price $y$ in terms of number of pages $x$.
Graph both of these equations on the same coordinate plane, with $x$ on the horizontal axis.
My report is $N$ pages long. Coincidentally, it turns out that the price of an $N$-page report is exactly the same, whether I print it at PrintCorp or at InkCorp. What is $N$?
How does your answer to part c appear in your graph? Explain.
Two values $x$ and $y$ depend on each other — the relationship $3x - 2y = 10$ is always true.
What is the value of $y$ when $x = 4$? What is the value of $x$ when $y = 4$? What is the value of $y$ when $x = 0$?
Plot the above points on a set of axes, with $x$ on the horizontal axis. Using your three points, estimate what $y$ would be when $x$ is 8, then use the equation to check your answer.
Do you think the relationship between $x$ and $y$ is linear? Justify your response.
Graph the line $y = - 2x + 12$ without using your calculator. Then:
Find a way to rewrite this equation
so that it’s in a similar form to the equation below:
$Ax+By=C$, where $A$, $B$, and $C$ stand for numbers.
What would be the values of $A$, $B$, and $C$?
If the equation $3 - 4x = 17y$ were written in a form similar to that in part a, what would $A$, $B$, and $C$ be?
Jake has a rule, µ, but he’s not saying what it is. However, when Mollie asked him what µ(4) was, Jake said, “57” and when Seth asked him what µ(12) was, Jake replied, “17.” Jake did confess to Mark that his rule followed a linear pattern.
Find a formula for the function µ:
µ($x$)=_______________
For what values of $x$ will µ output negative answers?
You are buying coffee beans — the minimum purchase at this store is 20 ounces. The price is set such that you can buy 3.5 ounces of coffee for one dollar. You also have a coupon for \$5 off your final price.
.Write an equation for $P$, the price you pay, in terms of $C$, the amount of coffee you buy.
Graph the equation with $C$ on the horizontal axis and $P$ on the vertical axis. Which values of $C$ are relevant to this situation? Which aren’t?
What’s the slope of your line? What are the units of the slope? Does it have a meaning that’s relevant to the situation?
Find the $P$-intercept of your equation. What does this number represent in the situation?
You will find some of the next few problems easier to solve if you can find a way to represent them visually.
One phone company charges a flat monthly rate of \$30 and a per hour charge of \$1.25. A competing company charges a flat monthly rate of \$45 and a per hour charge of \$0.75. Which company would you choose?
Which of the following are linear equations — equations whose graphs are lines — and why?
$y = {x^2}$
$x = 2y - 3$
$3x + 2y = 7$
A line has positive $x$- and
When you graph some linear data, the points $\left( {5,11} \right)$ and $\left( {11,21} \right)$ are on the graph. Will the point $\left( {32,55} \right)$ also be on the graph? How do you know?
A line contains the points $\left( {5,2} \right)$ and $\left( {c,10} \right)$. If the slope of the line is 4, what is c?
Back to problem 27. Find the slope of the line by taking the equation of the line to be $y = a + bx$, and using algebra.
Which line is steeper: $y = 3x + 6$ or $x = \frac{1}{3}y - 2$?
We have two lines, $2x - 10y = 14$ and $6 − 5 y = −x$. Which line is steeper?
Cecelia declares, “if I know a point on a line and I double the $x$-coordinate, it will be easy to find the $y$-coordinate that goes with it — just double the old $y$-coordinate.
Is Cecelia right? Try her principle with a few different lines.
Can you figure out for which kinds of lines Cecelia’s method works?
Two variables are said to be “directly proportional” if they have a constant, unchanging ratio. For example, if $\frac{x}{y} = \frac{2}{3}$, then $x$ and $y$ are directly proportional to each other.
Graph 4 solutions to $\frac{x}{y} = \frac{2}{3}$.
If $2x - 3y = 1$, are $x$ and $y$ directly proportional?
If $2x - 3y = 0$, are $x$ and $y$ directly proportional?
You have to work 210 hours before you start earning money. Then you earn $\$1$ for every 20 hours. Write an equation for how much you earn, $E$, in terms of the number of hours you’ve worked, $H$.
Consider the linear data below:
| $x$ | 1 | 2 | 3 | 4 | … |
| $y$ | 12 | 21 | 30 | 39 | … |
Write an equation for $y$ in terms of $x$. Then graph the line.
Draw a second line that is above the first line when $x = 2$, but below the first line when $x = 3$. Then write an equation for the new line.
A line contains the points $\left( {8,5} \right)$ and $\left( {c,c} \right)$.
If the slope is 2, what is $c$?
If the slope is 2, find the equation of the line.
Write an equation for the slope in terms of $c$.
Exploring in Depth
A line contains the point $\left( {1, - 8} \right)$. When $x = 2$, $y$ is still negative. When $x = 3$, y is now positive. Sketch a few pictures of possible lines. Now answer the following questions.
To the nearest tenth, what’s the smallest possible slope that the line could have?
To the nearest tenth, what’s the largest possible slope it could have?
There’s one point on the line $y = 10 - 2x$ where the $y$-value is 4 times bigger than the $x$-value. Find this point.
If 400 people come to a banquet, it takes 59 people to set up. If 722 people come to the banquet, it takes 87 people to set up. Assume the situation is linear and answer the following questions:
If 500 people come, how many people do you need to set up?
If 79 people set up, how many people can come?
If 1 person comes, how many people do you need to set up? (Remember that even if only 1 person comes, they still need people to set up the decorations, dessert table, etc.)
You buy your lunch at a salad bar, which charges a certain price per ounce — including the weight of the bowl. When you put 8.3 ounces of salad into the bowl, the price comes to \$6.78. When you put 10.5 ounces of salad into the bowl, the price is \$8.21.
What is the price charged per ounce of salad?
What is the weight of the bowl, in ounces?
Don’t use a calculator for this problem.
Find $2.\overline 3 - \frac{4}{3}$
Solve for $x$: $\frac{1}{x} = 3$
Simplify: $- (1 + 2x)( - 2x)$
Factor $12{x^2} - 42x$
Expand ${(x + 1)^2}$
If you feed a turtle $W$ worms, he’ll crawl 15.5 inches. If you feed him twice as many worms, he’ll crawl 40 inches. Assume the situation is linear.
Make a table and fill it in (some entries will have $W$’s instead of numbers).
How far will he crawl if you feed him 3 times as many worms? Explain.
If $W$ is equal to 7, how far will he crawl for 8 worms?
If $W$ is equal to 7, how many worms do you have to feed him for him to crawl 50 inches?
Show that if a line containing the point $\left( {{x_1},{y_1}} \right)$ has slope $m$, then an equation of the line is $y−y_1=m(x−x_1)$.