Introduction
The business of solving equations can sometimes be a simple matter, but at times can become quite complicated. It can range from the relatively simple task of finding a value of $x$ that satisfies the equation $3 + x = 7$ to a problem that turns out to be impossible, that of finding positive integers $a$, $b$, and $c$ that satisfy the equation, ${a^3} + {b^3} = {c^3}$.
Then there are those equations that have so many solutions that it would be impossible to write them all out. What if someone challenged you to find the two numbers they are thinking of and the only clue you had was that the sum of the numbers is 100? You are actually invited to solve the equation, $x + y = 100$; the possibilities are endless.
Or what if you were faced with the task of writing out all the solutions to the equation $x + 3 - 5 = 9x - 8x - 2$ or to the inequality $3x + 6 < 8$?
By way of review, solve each of the following equations and inequalities for the unknown letter. Remember to be particularly careful with the inequalities. In particular, when multiplying or dividing by a negative number, you always have to reverse the inequality. Why must this be so?
$2y - 3y = 7 + 4y$
$3.5x - 4 = 7 - 7.5x$
$5\left( {r - 5} \right) - 3\left( {2 - r} \right) + 35 = 0$
$3\left( {x - 4} \right) + 15 = 35 - 5\left( {2 - 5x} \right)$
$17x + 5 < 31x - 2$
$2\left( {3.5x - 7.5x} \right) + 4 > 1$
$8 - \left( {7 - n} \right) = 33$
$- {\textstyle{1 \over 3}}c = 17$
$- 3 + {\textstyle{d \over 7}} = - 12$
$3\left( {2 + 3x} \right) = 13 - 4\left( {3 - x} \right)$
Development
To write all the solutions to the equation $3x + 7 = 22$ is a pretty simple task, since $x$ can be replaced by only one number to make the equation work, namely 5. Check it out.
The question of what values of $x$ and $y$ make the equation $2x + y = 13$ work is a slightly more complicated question, and it is certainly no easy matter to find all the values of $x$ and $y$ that make the equation work.
Does $x = 3$, $y = 6$ work? How about $x = 7$, $y = - 1$? What about $x = \tfrac{1}{4}$, $y = \tfrac{25}{2}$? Justify your responses.
Find three more solutions to the equation.
What would be a systematic way of finding solutions? Use your method to find two other solutions.
By the way, a neat way to write a solution like $x = 7$ and $y = - 1$ is $(7,-1)$, with the $x$-value written first, followed by the $y$-value. The expression $(7,-1)$ is called an ordered pair. Any idea why?
Can you list all the solutions to the equation $2x + y = 13$?
The answer is probably no, since there are simply too many, but from your work in Lesson 1 you should know that there is a nice way to show off a whole bunch of them very quickly.
Show that $(-1,15)$ and $(10,-7)$ are both solutions to the equation $2x + y = 13$, and graph these two points. Now graph at least ten thousand solutions to the equation in less than ten seconds.
How accurate is your graph in problem 5? For example, suppose you wanted to determine whether the ordered pair $(\tfrac{1}{4}, \tfrac{49}{4})$ is a solution to the equation $2x + y = 13$. How much would you be willing to bet on the answer you obtained from your graph?
Now let’s look at the inequality $2x + y > 13$. Can you list all the solutions? If not, is there a nice way you can show off a whole bunch of them very quickly?
For the inequality $2x + y > 13$:
Does the ordered pair $\left( {5,2} \right)$ satisfy it? How about $\left( {7,1} \right)$?
List five ordered pairs that satisfy it.
Find three ordered pairs $\left( {x,y} \right)$ that satisfy it and are such that $2x + y$ is as close to 13 as you can get.
Then find three ordered pairs $\left( {x,y} \right)$ that do not satisfy it, but are such that $2x + y$ is as close to 13 as you can get.
Now draw a picture of a few thousand solutions to the inequality in problem 7.
You are used to graphing equations. The picture you drew in problems 7 and 8 is called the graph of the inequality $2x + y > 13$.
Practice
Find three different solutions to the equation $5x - 3y = 11$, including at least one integral solution (a solution consisting only of integers).
Using the method of problems 7 and 8, graph solutions of the inequality $5x - 3y < - 1$.
Graph solutions of the equation $x + 3y = 11$. Say whether or not the point $\left( {2821, - 937} \right)$ is on your graph.
Problems
The function $‡[x, y]$ is pretty weird: it totally ignores $y$, and just takes $x$, multiplies it by 5, and subtracts 4. Graph all of the ordered pairs $(x,y)$ that satisfy $‡[x, y]=10$.
For each of the following, create an equation in $x$ and $y$ that satisfies the given information.
$(\tfrac{3}{2}, -\tfrac{1}{2})$ is a solution.
$\left( {3, - 1} \right)$ is a solution.
Both $(\tfrac{3}{2}, -\tfrac{1}{2})$ and $\left( {3, - 1} \right)$ are solutions.
In what way(s) would a graph of $2x + y \geq 13$ be different from the graph of $2x + y > 13$? (You might find your work in problem 7 helpful here.)
Graph the solutions to the inequality $2x + y < 13$.
Problems that seem on the surface to be difficult can sometimes be easily solved by drawing a careful diagram. The next few problems underscore the value of that visual aspect.
Try to find an ordered pair $\left( {x,y} \right)$ that satisfies both of the equations $4x - 6y = 9$ and $-6x + 9y = -8$.
Find the ordered pairs $\left( {x,y} \right)$ that satisfy both of the inequalities: $2x + 3y > 12$ and $x + y < 6$.
Do the following two equations have any solutions in common? How many? If they have any solutions in common, find them. Be sure to check your answer. $$3x-y=-1$$$$x+5y=-3$$
Find the area of the region enclosed by the graph of the following system of inequalities. $4x + 5y \le 20$, $2x - y \ge - 4$, $y \ge 0$.
The dimensions of the bottom of a rectangular box are 10 in by 15 in. Find the height of the box if its total surface area is 525 in2.
How many points are on the line $y = 2x$ between $(1,2)$ and $(2,4)$? How about between $(1,2)$ and $(3,6)$? How about between $(1,2)$ and $(1.01, 2.02)$?
What’s the largest integer $x$ that solves the inequality $x < 5$? What’s the largest rational number that solves it?
If $x < y$, is it possible to find values of $x$ and $y$ such that $\frac{1}{x} > y$?
Jonathan claims that there is a certain ordered pair that satisfies all the equations $x+3y=19$, $2x-5y=5$, $x-2y=4$.
Either prove or disprove Jonathan’s claim.
The Linear Game
In this game, the host, Eva, thinks up a linear equation in two variables $x$ and $y$. She then invites a contestant, say Lewis, to come up with the equation using the following approach. Lewis calls out an $x$ or $y$ value and Eva tells him the corresponding $y$ or $x$ value.
For example, suppose Eva is thinking of the equation $3x - y = 11$ and Lewis says $x = 1$, then Eva says $y = - 8$, and if Lewis says $y = 3$, Eva says $x = \tfrac{14}{3}$. This continues until Lewis is able to figure out what Eva’s equation is.
How many tries does Lewis absolutely need to get Eva’s equation?
Below is a summary of four of the Eva-hosted games. In each case, guess Eva’s equation.
i.
| Lewis | $x = 2$ | $y = 3$ | $y = 0$ |
| Eva | $y = 1$ | $x = -1$ | $x = \tfrac{7}{2}$ |
ii.
| Lewis | $y = 2$ | $x = 3$ | $y = 7$ |
| Eva | $x = - 5$ | impossible | $x = - 5$ |
iii.
| Lewis | $y = 3$ | $x = -1$ | $y = -2$ |
| Eva | $x = 2$ | $y = 4$ | $x = 17$ |
iv.
| Lewis | $y = 2$ | $y = 3$ | $x = 0$ |
| Eva | impossible | impossible | $y = 7$ |
It seems that there might be a more efficient way than Lewis’s to find Eva’s equation. What would be a good strategy?
Play the linear game with a classmate.
The points $(1,5)$ and $(-2,11)$ satisfy the same linear equation. Find another point that does.
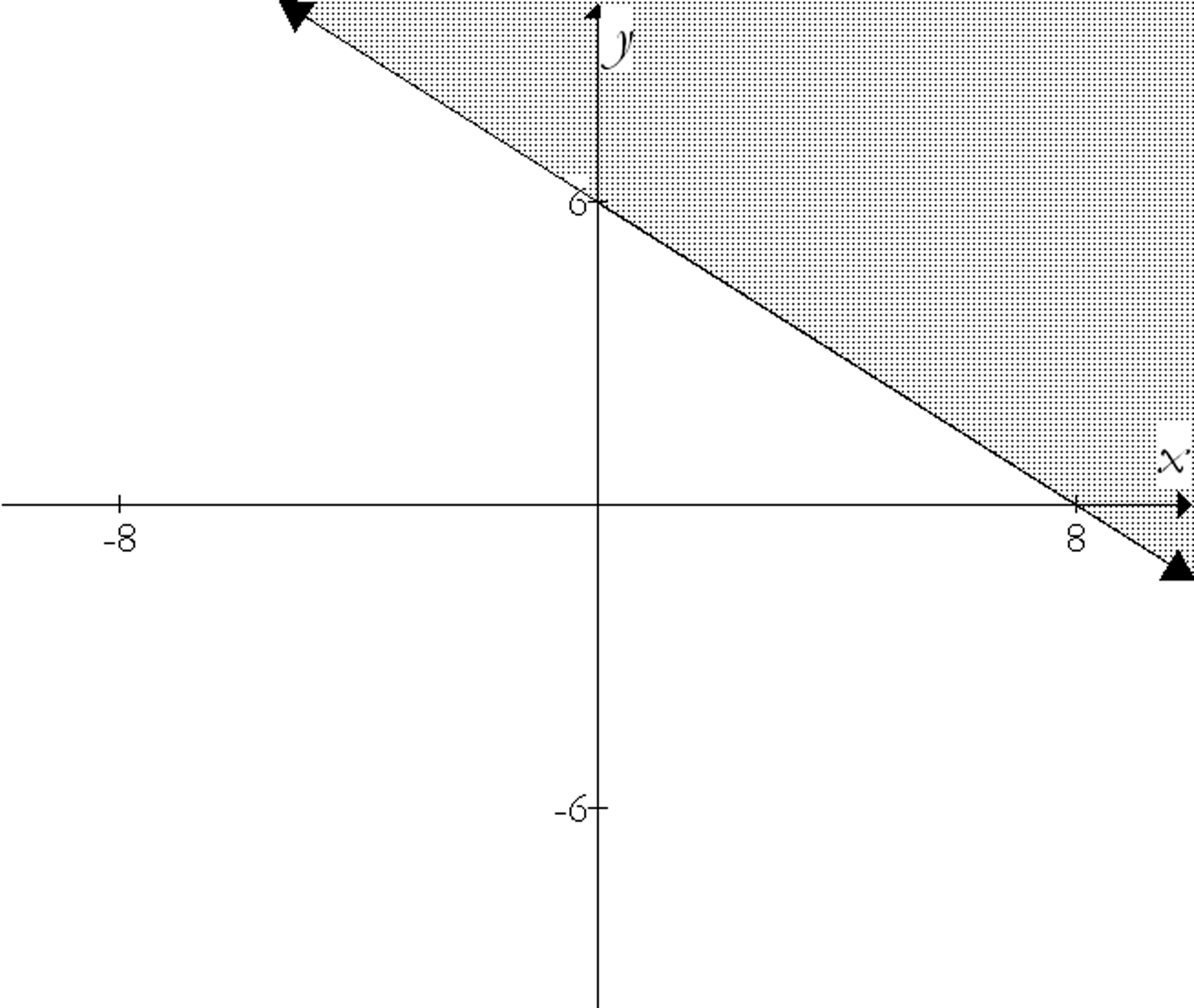
Write an inequality for the shaded area below.
Thinking about the way you solve for $x$ in the equation $2x + 3x = 7$ might help you solve the following equations. Of course your answer would involve constants other than numbers. Try to solve each equation for $x$.
$ax + 3x = 7$
$2x + bx = 7$
$ax + bx = 7$
Ayana is thinking of a number. If she decreases it by 5 and then multiples by 11, the result is the same as when she decreases it by 3 and then multiples by 7. What number is Ayana thinking of?
For each statement below, find what number $c$ has to be to make it true.
The line $3x + y = c$, for
some
number
The graph of $cy - 2x = 1$ contains the point $(7,3)$.
The graph of $2y = cx + 9$ has an
The line $y = 3x + c$ contains the point $(2,7)$.
Two points (not necessarily lattice points) with $x$- and $y$-coordinates both between 0 and 10 inclusive are chosen. Find the probability that $3x + 5y$ will be less than 15.
Exploring in Depth
What do you think the graph of the equation $x = 4$ would look like in 3-dimensional space?
What do you think the graph of the equation $x + y = 4$ would look like in 3-dimensional space?
I have $X$ pens and $Y$ CD’s that I want to sell. Pens sell for \$1 and CD’s sell for \$6. Total, what I have is worth \$71.
Would it be possible for me to have 300 pens? 30 pens? 35 pens?
Write one equation that expresses the situation, and graph the equation.
I am $X$ years old and my younger brother is $Y$ years old. If you add 3 to my age, you’d get the same answer as if you doubled his age. Write this as an equation and graph the equation. Then find two possible solutions for our ages.
The line whose equation is $ax + by = 3$ contains the points $(5,1)$ and $(-9,-3)$. Find the values of $a$ and $b$.
Draw a graph of the solutions of the equation ${x^2} + {y^2} = 9$.
Draw a graph of the solutions of the inequality $y \le {x^2}$.
Suppose $ax - {a^2} = bx - {b^2}$. For the indicated values of $a$ and $b$, find the value of $x$ that satisfies the equation, and complete the chart below.
| $a$ | 1 | 2 | 1 | 3 | 2 | 2 |
| $b$ | 7 | 1 | 3 | 2 | 4 | 5 |
| $x$ |
Again, suppose $ax - {a^2} = bx - {b^2}$:
Based on your results in problem 39, guess what $x$ would be when you solve the equation for $x$ in terms of $a$ and $b$.
Check to see that your guess in part a works.
Two points (not necessarily lattice points) with $x$- and $y$-coordinates both between 0 and 12 inclusive are chosen. Find the probability that, while the $y$-coordinate is less than twice the $x$-coordinate, the sum of the $x$- and $y$-coordinates is greater than $9$.
Don’t use a calculator for this problem.
Add $3\frac{2}{3} + \frac{7}{6}$
In February, all the menu prices at Danny’s diner increased by 10%. Then Danny got worried, because with higher prices not as many customers came, so in March he decreased all the prices by 10%. Are his customers now paying less than, more than, or the same amount as they were in January?
Factor ${x^2} - 81$
Solve for $x$: $\frac{1}{x} + 2 = 4$
What are the two possibilities for $x$ if $|x - 3| = 4$?