Introduction
How would you define parallel lines? How would you decide if two lines were parallel?
Euclid, Ancient Greek geometer $extraordinaire$, defined parallel lines as lines in a plane which never meet, even when extended indefinitely. Line segments are parallel if they lie on parallel lines.
It was hard for those Greeks to determine if lines were parallel — after all, how could you show for sure that lines never met? What if you thought that lines were parallel, but actually they met at a point 100 miles away? This would happen if lines were very close to being parallel, but not quite.
Euclid’s parallel lines remain the same distance apart, no matter where you take the measurements. (Think of train tracks with crossbars of equal length.) That might give a more practical way to tell if two lines are parallel — measure their distance apart in two different places and see if you get the same thing. But even that would not be without its problems. Your measuring instruments might not be accurate enough to tell if lines are just skewed enough to meet 100 miles away.
To illustrate how difficult it can be to tell even if two short line segments are parallel, look at the following pair, below.
In fact, the line segments above were drawn so as NOT to be parallel to one another. They are just slightly off.
In the 1600s, the French mathematician and philosopher Rene Descartes changed the way people thought about — and did — geometry. The story goes that he was lying in bed one day, staring at the ceiling, and realized that he could describe the position of a bug on his ceiling by counting the number of ceiling cracks up and the number of ceiling cracks over.
If you had two line segments on a $grid$, as below, and knew the coordinates of a few points on each line, would you now have a method to decide if they were parallel?
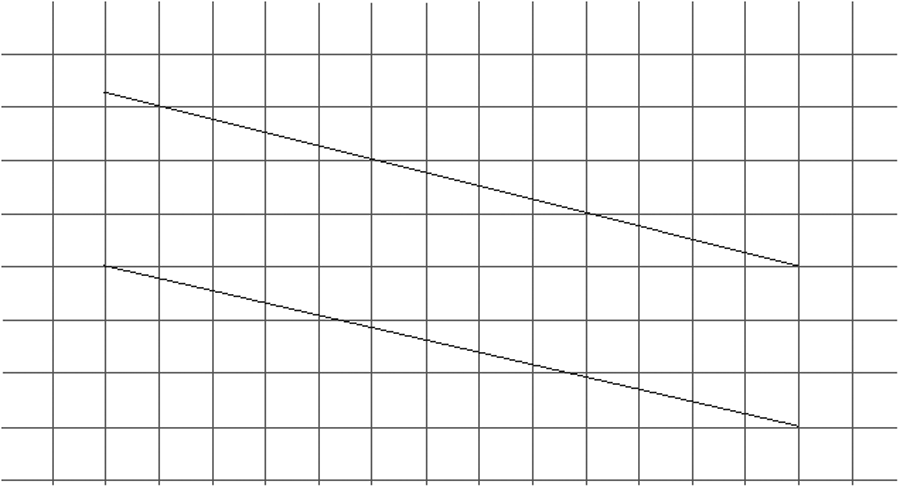
Descartes’s wonderful idea allowed someone to take a geometric shape — a line — and describe its position exactly by overlaying a grid — a coordinate system. Since these coordinates had numbers attached, all of the sudden people were able to apply much of what they already knew about algebra to geometry. Descartes had allowed people to use multiple points of view when considering geometry problems, switching freely back and forth between an algebraic perspective and a geometric perspective. And, when you thought about the previous problem, so did you.
The rest is history.
Development
Say you live in a city where the streets are laid out in a square grid pattern. You start at your house and walk two blocks north, then three blocks east.
Draw a picture of this path on a piece of graph paper. What’s the slope of the line segment connecting your house and your ending point? How would you describe its direction?
Your friend lives two blocks south of you. She starts at her house, then follows the same pattern as you — two blocks north and three blocks east.
Draw a picture of your friend’s path, on the same paper as yours.
Is there a sense in which your path and your friend’s paths are “parallel” (even though neither of you went in a straight line)? Explain this.
Draw the points $\left( {1,2} \right)$ and $\left( {2,5} \right)$. Draw the line through them — this is line $m$.
Line $n$ contains the point $\left( {3,1} \right)$ and is parallel to line $m$. Draw line $n$. The point $\left( {5,c} \right)$ is on line $n$. Find $c$.
What are the slopes of lines $m$ and $n$?
Discuss this question with a partner: Suppose that you have two lines, one with slope 5 and another with slope $\tfrac{11}{2}$. Will they have to meet somewhere? Try drawing several pairs of lines with these slopes. What keeps happening?
Based on your thinking in the previous problems, say what must be true for two lines to be parallel.
What about lines that are perpendicular to each other — that is, lines that cross at a 90 degree angle?
Can two lines, each with positive slope, be perpendicular? How about two lines, each with a negative slope? Explain with a picture.
Draw the line $y = 2x$.
Is $y = - 2x$ perpendicular to this line? How about $y = \frac{1}{2}x$?
Take some guesses at the equation for a line that really might be perpendicular to the line $y = 2x$. Check your guesses by drawing this line on the same coordinate system.
We found that parallel lines have the same slopes. Do the slopes of perpendicular lines also have some relationship? Instead of trying to find a general rule right away, let’s simplify the problem by making up an example.
Using graph paper, draw a line segment (not horizontal or vertical), and use a measuring tool (a protractor? the corner of a piece of paper?) to draw another line segment perpendicular to the first. Then calculate the slopes of the two segments you drew. What do you suppose would be more helpful in looking for patterns — writing the slopes in fraction or decimal form?
By creating other examples, or by looking at the results of the examples your classmates made up, conjecture a relationship between the slopes of perpendicular lines.
Try out your conjecture by using it to answer the following questions. Suppose that lines $p$ and $q$ are perpendicular.
What’s the slope of line $p$ if line $q$ has slope $\frac{3}{5}$?
What’s the slope of line $p$ if the equation of line $q$ is $y = \frac{1}{3}x + 1$?
What’s the slope of line $p$ if the equation of line $q$ is $y = - 2x + 1$?
Check your answers to the previous problem by graphing lines that fit the conditions of parts a, b, and c. Now do you think your conjecture is true? If not, use this new information to change your conjecture.
We’ve already found a way, using slope, to describe the direction of your path through a city. We can also use information about evenly-spaced city blocks to calculate your distance.
Starting at your house, you walk 2 miles west and 6 miles north. How far away are you now from your house (measuring distance along a straight path)?
Your house is at the point $\left( {1,5} \right)$. You walk to the point $\left( {10,4} \right)$.
How far east or west did you go?
How far north or south did you go?
What’s your distance from your house?
Draw the points $\left( { - 2,3} \right)$ and $\left( {2,6} \right)$. Find the distance between them.
Finally, you can calculate the position $halfway$ between two locations in a city (or on a graph). This position is called the midpoint. We can also speak of the midpoint of a line segment connecting two points. Soon, we’ll find a formula that tells you how to find the midpoint of a segment joining $(x_1,y_1)$ and $(x_2, y_2)$. But first let’s try some simpler problems.
What would be the midpoint of $\left( {1,5} \right)$ and $\left( {6,10} \right)$? Create some other, simple problems like this where you have to find the midpoint.
What would be the midpoint of $\left( {1,0} \right)$ and $\left( {3,y} \right)$? Of $\left( {x,4} \right)$ and $\left( {3,y} \right)$?
What’s the midpoint of $(x_1,y_1)$ and $(x_2,y_2)$?
Write in symbols what the $x$- and $y$-coordinates of the midpoint would be.
Compare your answer with what other people got. If there are different answers, see if you can do some algebra to make them look the same.
Practice
What is the distance between
$(-2, -5)$ and $\left( {6,10} \right)$?
$(-2, -5)$ and $\left( { - 6, - 10} \right)$?
Lines $c$ and $d$ are perpendicular. What’s the slope of line $c$, if…
line $d$ has slope $1\frac{1}{2}$?
line $d$ has slope $–.25$?
line $d$ has slope $.24$?
Two perpendicular lines intersect at the point $\left( {1,2} \right)$. The first line also contains the point $\left( {5,10} \right)$. Give the exact coordinates of another point on the SECOND line.
Line $p$ goes through the points $C\left( {1,8} \right)$ and $D\left( {13, - 4} \right)$. Line $q$ goes through the points $E\left( {-2, 6} \right)$ and $F\left( {10, - 7} \right)$.
Make a sketch.
They sure look parallel. Are they?
How about angle CDF? Is it a right angle? Support your answer with mathematical evidence.
Line $p$ goes through the points $\left( {2,4} \right)$ and $\left( {6, - 2} \right)$.
Find two points on line $p$ other than the given ones.
Find two points that would be on a line parallel to line $p$.
Find two points that would be on a line perpendicular to line $p$.
There are four lines $l$, $m$, $n$, and $p$ with slopes $\frac{1}{3}$, $-1\frac{1}{2}$, $\frac{2}{3}$, and $-3$, respectively. Are any of the lines parallel? Perpendicular?
The town of Metropolis is laid out as follows. The gridlines are roads, but if you’re walking you can cut across the blocks diagonally.
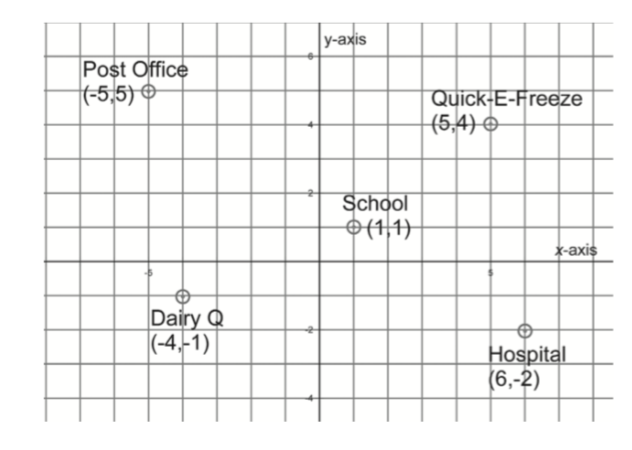
What’s the walking distance (how many “units”) from
- The Post Office to School?
- The Quick-E-Freeze to the Dairy Q?
- The Quick-E-Freeze to the Hospital?
Which two buildings in Metropolis are the farthest apart, measured by walking distance? How far apart are they?
You’re at school and want a cran-root-beer Squidgy. Measured by walking distance, which is closer — the Dairy Q or the Quick-E-Freeze?
Say that you’re driving now and can’t cut across the city blocks. Which involves the shorter trip from the school — the Dairy Q or the Quick-E-Freeze?
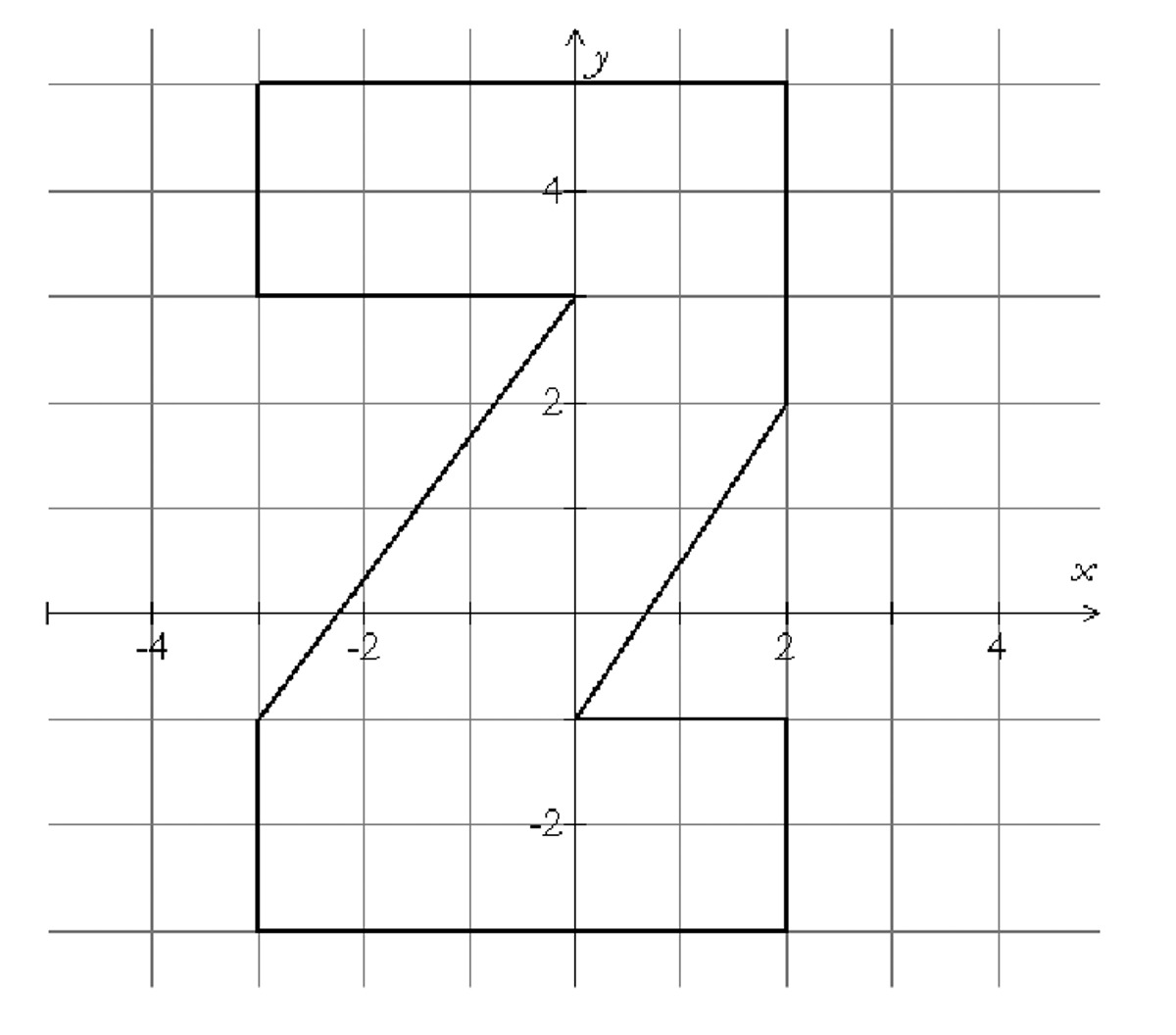
Here’s the design for the Varsity letter at Ziegelbawr High.
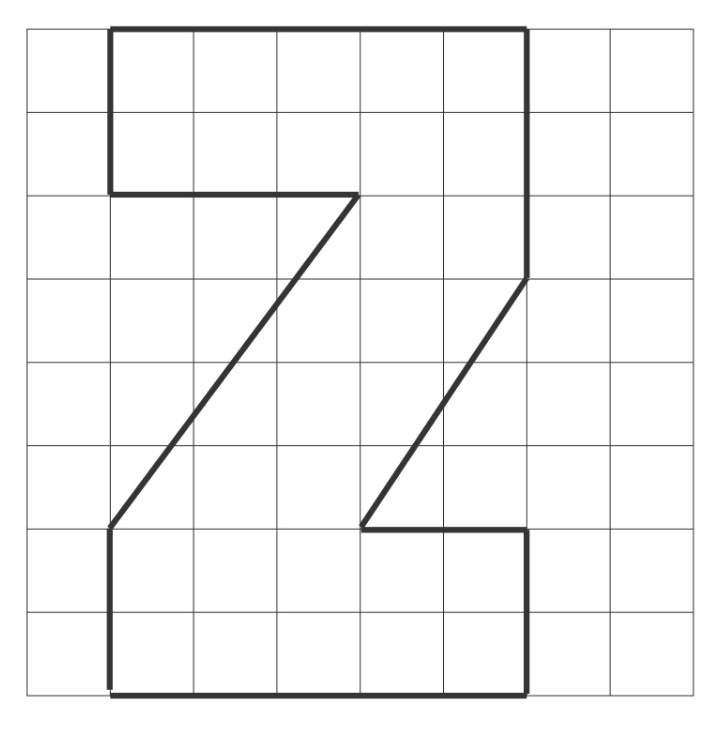
The diagonal lines appear to be parallel. Are they?
What’s the perimeter of the letter?
A triangle has vertices at $\left( {1,3} \right)$, $\left( { - 3,14} \right)$, and $\left( {-1,-5} \right)$. Find its perimeter.
Problems
Line $p$ passes through $\left( {0,0} \right)$ and $\left( {2,6} \right)$. It is parallel to line $q$, which passes through $\left( {6,1} \right)$ and $\left( { - 9,m} \right)$. Find $m$.
Prove that $\triangle ABC$ is a right triangle if $A = \left( {11, - 18}\right)$, $B = \left( {9,3}\right)$, and $C = \left( {-12, 1}\right)$.
You’ve found lots of distances over the course of this lesson.
Find a formula for the distance between any two points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$. As a suggestion, you could make up some simpler problems first.
If it isn’t this way already, write your formula in the form “$d = ...$”
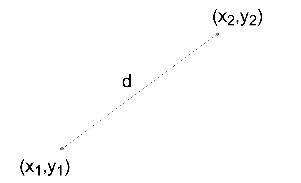
The formula you wrote in Problem 31 is sometimes called the Distance Formula.
The line $y = 3x - 4$ contains the points $\left( { - 3,w} \right)$ and $\left( {4,r} \right)$.
Find $w$ and $r$.
What is the distance between these two points?
Find the midpoint of the two points.
What’s the distance from the midpoint in part c to $\left( { - 3,w} \right)$?
You’ve probably noticed already that it can be extremely helpful to draw pictures in solving these problems. For instance, in the previous problem, you may have sketched the line and the approximate location of the points before solving for $w$ and $r$. While that wasn’t strictly necessary to solve the problem, it helps you to get a handle on it. For the next five problems, visualizing the situation by drawing a picture or adding things to a picture will make it much easier to decide how to proceed.
Consider the point $\left( {0,2} \right)$. If that point was on a line whose slope was 4, find:
The equation of that line.
The equation of another line through $\left( {0,2} \right)$, perpendicular to the first line.
Two bugs start at the point $\left( {3,5} \right)$. One travels down at a slope of $–2.5$, and the other takes a path perpendicular to the path of the first ant. How far apart are their $x$-intercepts?
A line’s $x$-intercept is –5. It has a positive
Is a line with a slope of $\frac{10}{4}$ steeper or shallower than a line with a slope of $\frac{5}{2}$? How does a line with a slope of $2.5$ compare?
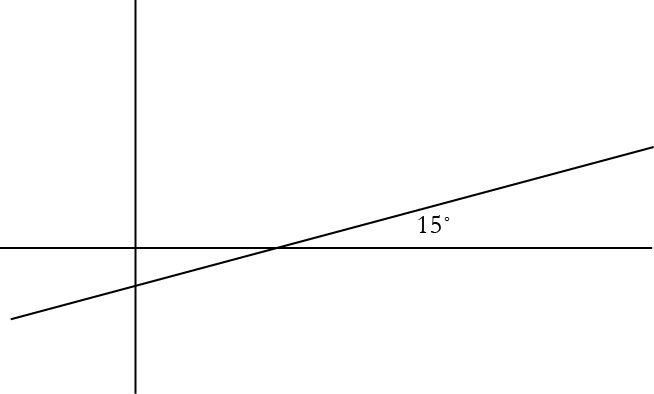
Say that a line makes an angle of 15 degrees with the $x$-axis. If you draw another line that makes an angle twice as big, 30 degrees, with the $x$-axis, will the slope of the line double as well?
For most of the problems remaining in this lesson, you will probably want to draw a picture. But even in most of the problems above, there was work left to do after the picture was drawn. The facts you now know about the slopes of parallel and perpendicular lines give you tools to use algebra to solve problems, as well. Sometimes this will be required, as in the case where your drawing suggests that a line passes through a certain point, but you’ll need to try algebra in order to make certain that it wasn’t just close. In the four problems that follow, don’t forget to draw a picture first, but you will also find representing relationships like slope and midpoint symbolically to work to your advantage.
If the line through $\left( {8,c} \right)$ and $\left( {6,4} \right)$ is parallel to the line through $\left( {6,8} \right)$ and $\left( {12,18} \right)$, then what must $c$ equal?
A triangle is formed by the lines $x = - 5$, $2y = x + 1$, and one other line. It has a right angle at the point $(5,3)$. Find the other two vertices of the triangle.
The line containing the points $\left( {4,1} \right)$ and $\left( {2,10} \right)$ is perpendicular to a line containing the point $\left( { - 3,7} \right)$. Find where this second line crosses the line $y = x$.
What value of $k$ will make the line containing points $\left( {k,4} \right)$ and $\left( {2,1} \right)$ parallel to the line containing $\left( {0,3} \right)$ and $\left( {k,9} \right)$?
Don’t use a calculator for this problem.
Divide $\frac{5}{2}\div\frac{1}{2}$
Simplify $(-x)(5+x)(-3)$
Factor ${x^2} - 8x + 16$
Solve for $x$: $\frac{3}{x} + 1 = 7$
What are the possibilities for $x$ if $\left| {x - 3} \right| < 4$?
Slopes can be represented as decimals as well as fractions.
Find three points with integer coordinates that the line $y = 2.5x + 1$ goes through.
Find three points with integer coordinates that the line $y = 1.1x + 3$ goes through.
Which two slopes in the list below represent lines that are almost perpendicular? No Calculators!
$\frac{2951}{986}$
$\frac{{.25}}{{.76}}$
$\frac{{ - 7428}}{{22305}}$
$\frac{{ - 2,994,852}}{{5,987,134}}$
Line $p$ has a slope of $\frac{7}{5}$ and is parallel to line $q$, which has a slope of $\frac{{119}}{a}$. Find $a$.
In problem 27, you realized that the diagonal lines in the Ziegelbawr High Letter (see below) are not quite parallel. If they’re not parallel, then they must meet somewhere. So where do they meet — above the “Z” or below? How do you know?
The following pretty picture was made by connecting the midpoints of adjacent sides of a square, then repeating the process on the new quadrilateral formed, etc.
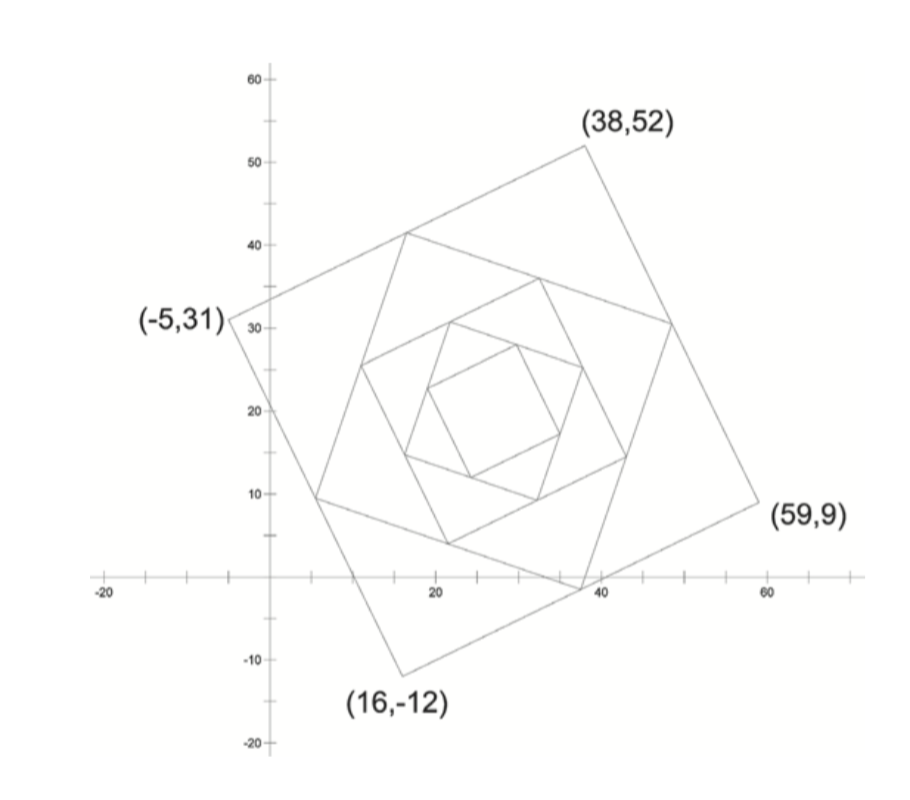
Is the second-biggest quadrilateral a square? (That is, are its sides perpendicular and are they the same length?)
Are the sides of the third-biggest quadrilateral parallel to the sides of the original square?
Will all the quadrilaterals you draw be square, even the 100th one? How can you be sure?
You have a square dartboard with corners at (0,0), (0,20), (20,0), and (20,20). Find equations for the boundaries of a “target” shape to hit within the dartboard using the following restrictions:
You may not use any vertical or horizontal lines, even the edges of the dartboard. The probability of hitting the target (assuming you’ll hit the dartboard) is 1/2.
You may not use any vertical or horizontal lines, even the edges of the dartboard. The probability of hitting the target (assuming you’ll hit the dartboard) is 1/4.
Below is Metropolis again. You’re exactly halfway between school and the post office. How far is the walking distance to the Dairy Q?

You’re standing at the point $\left( { - 2,3} \right)$ on the grid on the Metropolis grid (see previous problem). Gripped by the beautiful results you’ve discovered about slope, you decide not to head for the Dairy Q but in a direction perpendicular to the line between school and the post office. This takes you close to the Dairy Q but not quite.
Find an equation for the line that describes your new path.
What are the intercepts of this line?
When you’re at the $x$-intercept, are you closer to school or to the post office?
Is the result you found in part c just a coincidence? For which points on this line would you be closer to school? What is going on here?
Suppose you had a square that was 1 unit in length on each side. What would the length of a diagonal be? Can you find the length of the diagonal of the square whose sides are of length $d$?
Do the points $\left( {0,0} \right)$, $\left( {3,4} \right)$, and $\left( { - 1,1} \right)$ form an isosceles triangle? That is, are any two sides of the triangle equal in length?
Which of the following are equal to each other?
$\frac{{d-b}}{{c - a}}$
$\frac{{b - d}}{{a-c}}$
$\frac{{d - b}}{{a - c}}$
$\frac{{b - d}}{{c - a}}$
The function Slope($c$) takes a line $c$ and outputs the slope of line $c$.
.Find ${\rm{Slope}}(3x+7y=21)$.
Make up an equation for a line $d$ such that ${\rm{Slope}}(d) = \frac{1}{{{\rm{Slope}}}(3x + 7y = 21)}$.
Lines $e$ and $f$ are perpendicular. Find the value of ${\rm{Slope}}(e) \cdot {\rm{Slope}}(f)$.
Find the equation of the line passing through $\left( {2,5} \right)$ that is parallel to $y = 4x - 6$.
The slope of the line $2x + 5y = 10$ added to the slope of the line $kx + 8y = 23$ is zero. Find $k$.
Exploring in Depth
Find the area of the triangle in Problem 30.
Starting at the point $\left( {3,4} \right)$, you run in a straight line to the point $\left( {5,2.5} \right)$, running a 10-minute mile. (A mile is a unit on the plane). Then, you run in a straight line to the point $\left( {x,0} \right)$, running an 8-minute mile. The total time you ran is 1 hour and 15 minutes. Find $x$.
A point’s $y$-coordinate is 2 more than its
The midpoint of points $A$ and $B$ is $\left( { - 20,6.5} \right)$. The coordinates of point $A$ are $\left( { - 85,52} \right)$. What must be the coordinates of $B$?
The point $\left( {x,0} \right)$ is equidistant to — equally far from — $\left( { - 1,0} \right)$ and $\left( {5,1} \right)$. Solve for $x$.
Why do you think the definition of slope is as defined — “change in $y$ over change in $x$ ” — and not vice versa, “change in $x$ over change in $y$”?
The point $\left( {7,4} \right)$ below represents your location, and the line represents a river. (The scale on this graph is 1.)
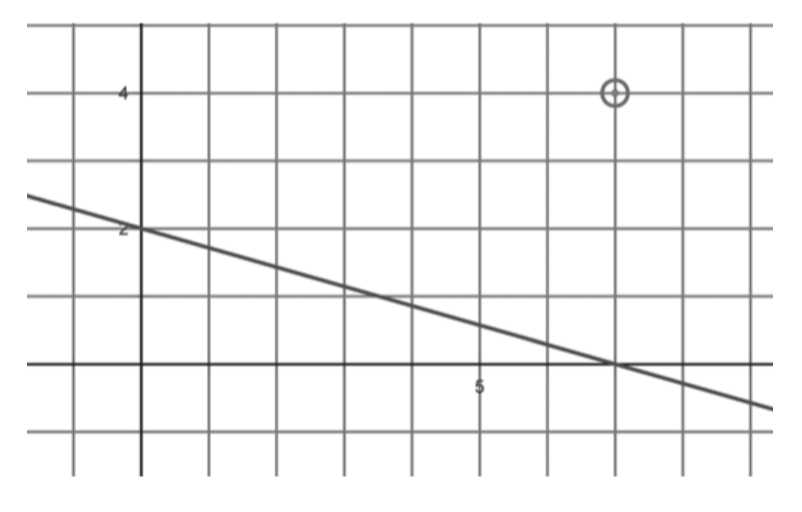
Write an equation for the river’s line.
Draw a path that you would walk to get as quickly as possible to the river. What is the slope of this path? What is an equation for this path?
Use your calculator to see the coordinates of the point where you would reach the river. Then find your distance from the river.
Describe a general strategy for finding the distance from a point to a line.
Metropolis, again! In Problem 50, you found an equation for your path starting from $\left( { - 2,3} \right)$ and perpendicular to the line containing the school and post office. With luck, you found it to be $y = \frac{3}{2}x + 6$. At what point on this line are you closest to the Dairy Q?
Can you find a formula, like the midpoint formula, that gives the coordinates of a point one-third of the way of the distance between two points? Be sure to test your formula on some specific points.
Remember that another way of determining if two lines are perpendicular is if their slopes multiply to -1.
Are lines with a slope of .111… (the 1’s go on forever — this number can also be written as $.\overline {111} $) and a slope of -9 exactly perpendicular?
What slope is perpendicular to a line with slope $1/9$?
Now determine the decimal equivalent of $1/9$.
Are your answers to the previous questions consistent?