Introduction
In the previous lesson, you learned about parallel and perpendicular lines. A pair of lines that are parallel never meet; other pairs of lines that you can draw on paper eventually will. You also learned that you can tell if lines are parallel by checking their slopes. The lines below aren’t on a coordinate system, so you won’t be able to check their slopes. However, to prove that they are not parallel, you could extend them to a point where they meet.

Place an extra piece of paper next to the picture above. Then, using a straightedge, pick two non-parallel lines and extend them until they finally meet. How far away from the edge of the picture did they meet?
Development
Will the real square please stand up? One of these figures is a square. The other is an impostor.
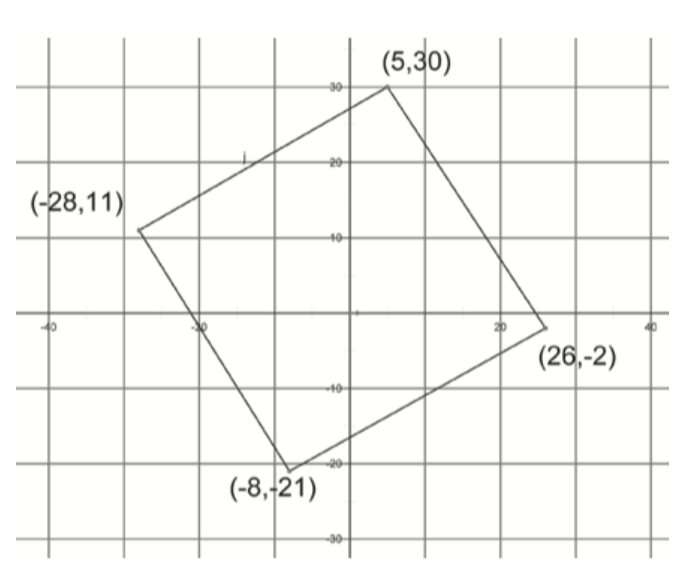
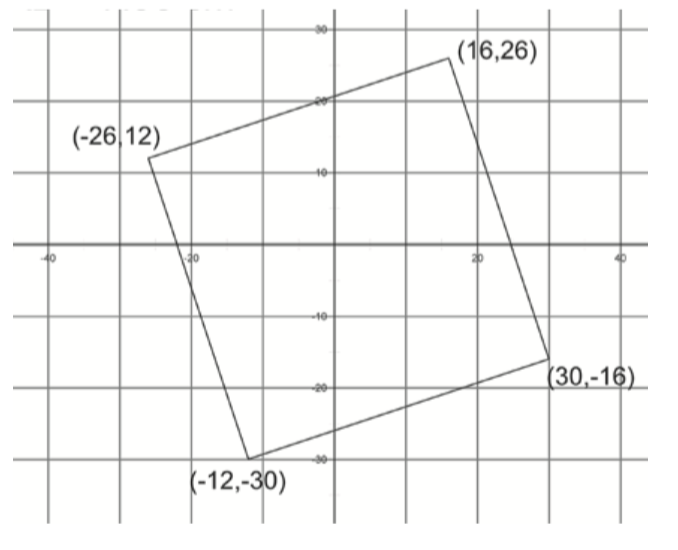
Find a way to determine which one is the square. Keep in mind that measuring with a ruler will not be accurate enough.
Here’s another figure which really is a square:
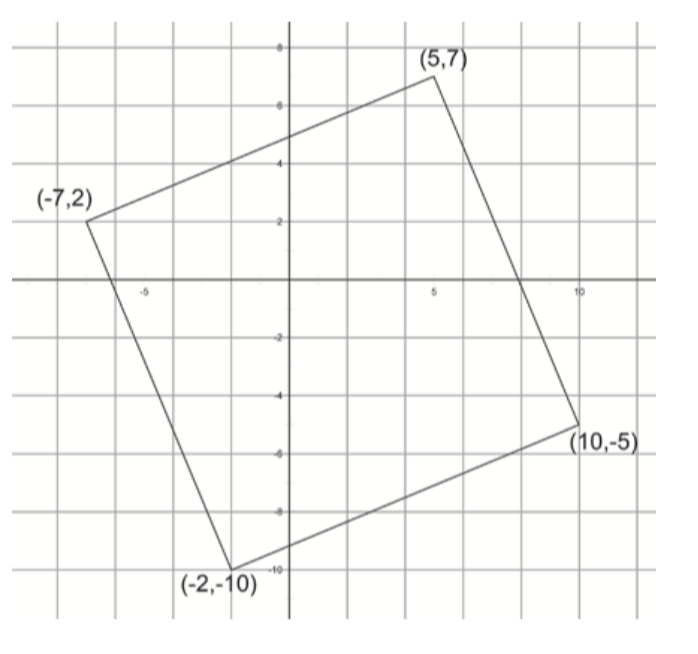
Or is it? As you have seen, it can be hard to tell.
What would you have to check to $prove$ that this is indeed a square? Do so.
In the previous problem, it wasn’t enough just to show that all the sides were the same length. Can you draw some four-sided figures, other than squares, where the sides are all the same length? Do you remember what such figures are called?
Similarly, it wasn’t enough to show that all of the angles were 90 degrees. Draw some four-sided figures other than squares with four 90-degree angles. What are they called?
Appearances can be deceiving. When confronted with a diagram, you should never assume what is not explicitly stated. You can’t be sure that you really have parallel lines, segments of the same length, etc. That is, you can’t be sure unless you prove it!
For example, a square is defined as a quadrilateral with four equal sides and four 90-degree angles. So to prove that something is a square, you need to: 1) Check that it has four sides, 2) Show that the sides have the same length (using the distance formula, for example), and 3) Show that all angles are 90 degrees (by comparing slopes, for example).
To prove that something is not a square, you only need to show that it fails on at least one of the counts above. So, for example, if you used the distance formula to show that two sides of a figure were of two different lengths, you would have already proved that it is not a square — no need to check the other criteria.
Use the definition of a square to do the following:
Prove that the four-sided shape with vertices on $\left( {3,0} \right)$, $\left( {7,3} \right)$, $\left( {4,7} \right)$, and $\left( {0,4} \right)$ is a square.
Make up your own square, then construct an argument to prove to someone else that it is a square.
How would you define a rectangle?
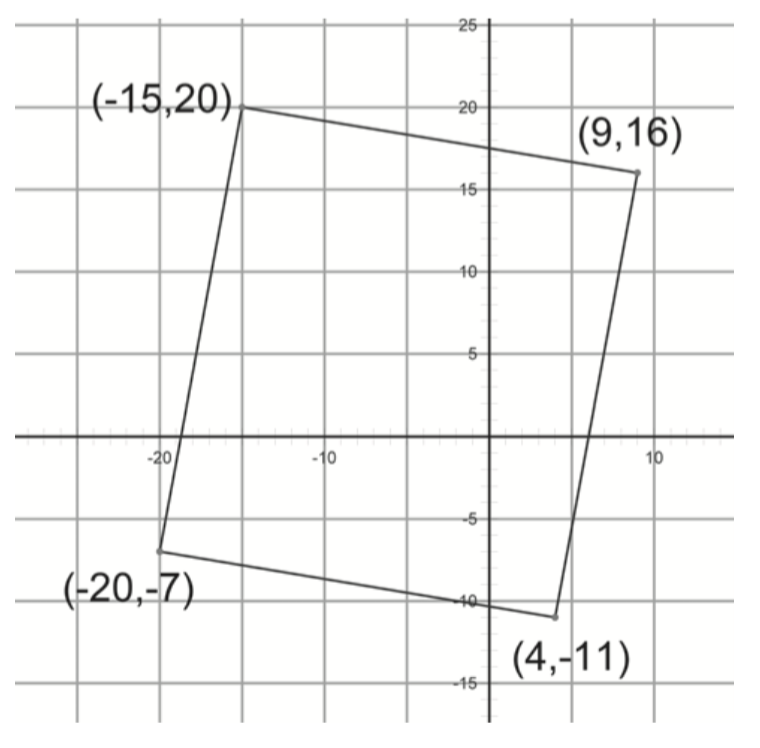
Here are the supposed corners of a rectangle: $\left( { - 32,52} \right)$, $\left( {74,138} \right)$, $\left( {117,85} \right)$, $\left( {11,-1} \right)$. Is it really a rectangle? Prove it.
Here is a picture of the rectangle from problem 7 with the diagonals drawn in. Do they look the same length to you? Either prove that they are the same length, or show that they are not.

Prove that the line segment drawn from $\left( { - 10,28} \right)$ to $(4,4)$ has the same midpoint as the line segment drawn from $\left( {-7,-4} \right)$ to $\left( {1,36} \right)$.
In middle school, you learned about parallelograms, rhombuses, and trapezoids. Come up with a definition for each.
Practice
In the following set of questions, you should either PROVE that the shape is what you think it is or give mathematical evidence to show that it is not. It may help you to start by drawing a diagram.
Are $\left( {10,2} \right)$, $\left( {12,42} \right)$, $\left( { - 28,44} \right)$, and $\left( {-30, 4} \right)$ the corners of a square?
In the figure below, is ABCD a rectangle?
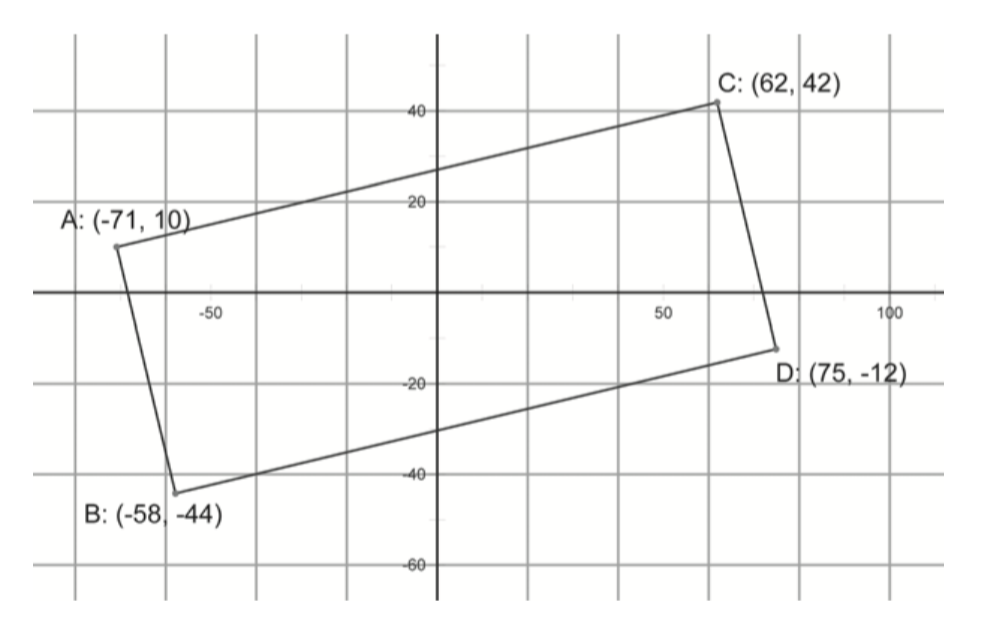
In the figure below, is ABCD a square?

In the figure below, is CDE isosceles?
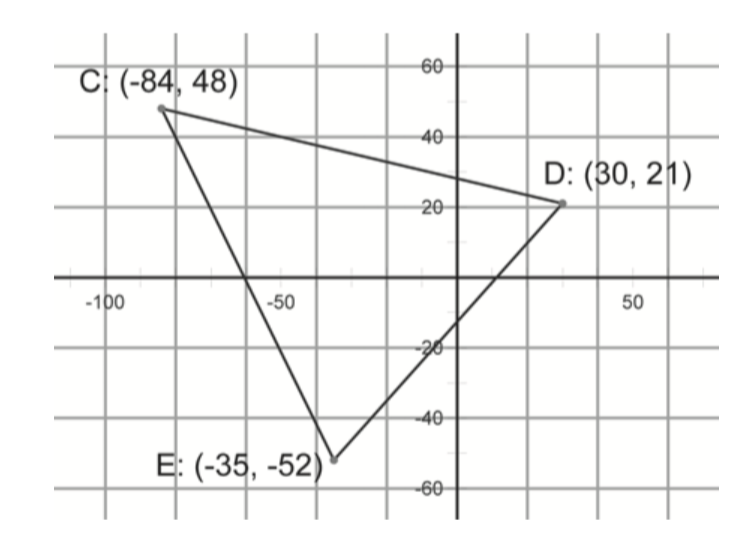
Are $\left( {-3,-1} \right)$, $\left( {14,12} \right)$, $\left( {18,20} \right)$, and $\left( {1,14} \right)$ the corners of a parallelogram?
Do some calculations to prove what, in fact, each of the following shapes is. Make sure you’ve shown the shape satisfies each part of the appropriate definition in Problem 10.

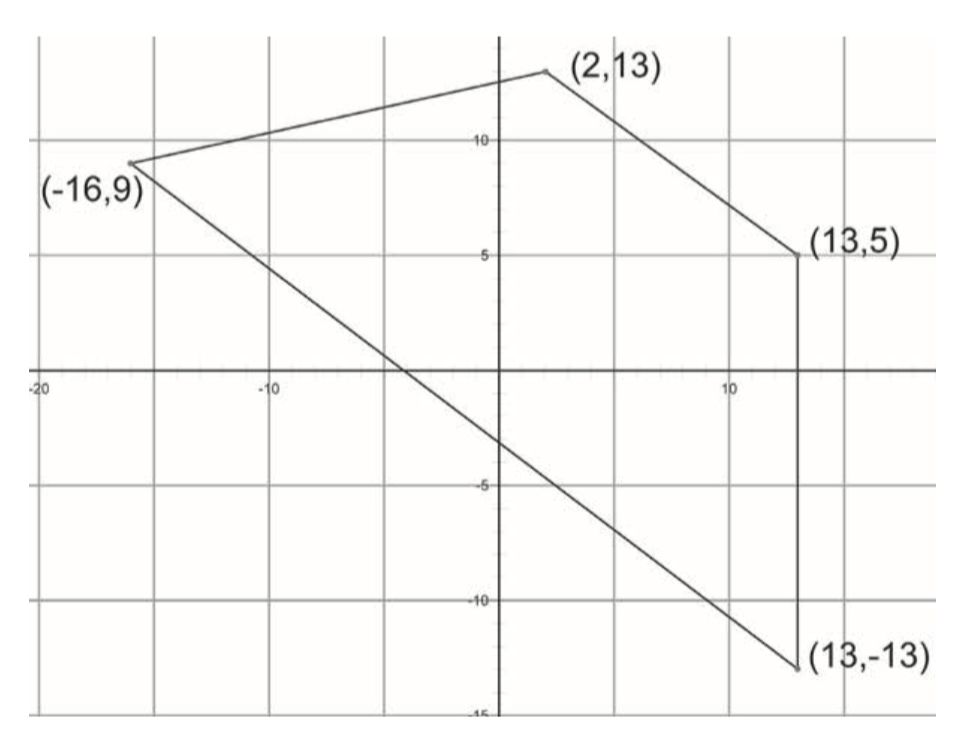
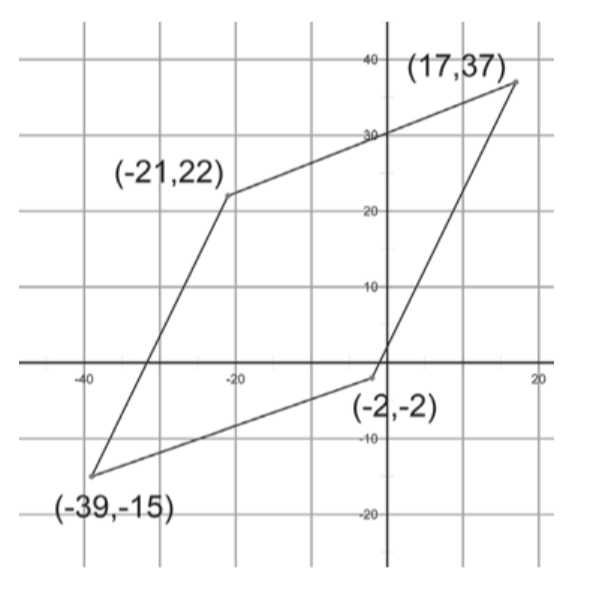
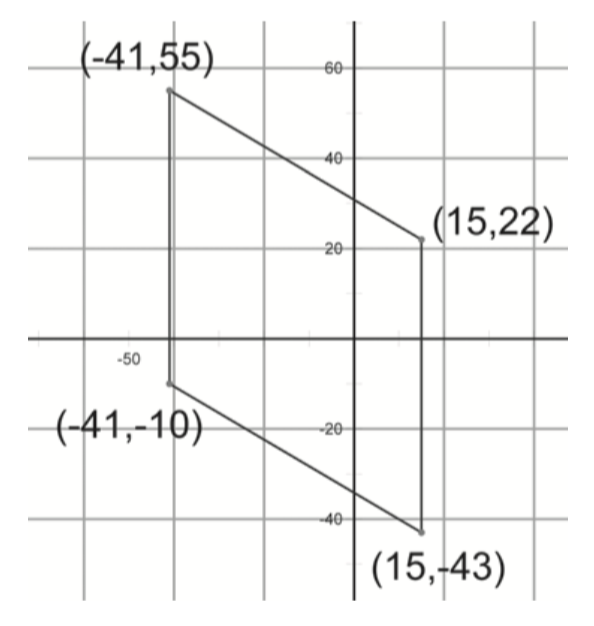

Going Further
Could we prove that the diagonals of $any$ rectangle are the same length as each other? One thing we could do would be to try another example. Let’s take another rectangle of a different size, say the one defined by $\left( {3,4} \right)$, $\left( {9,7} \right)$, $\left( {8,9} \right)$, and $\left( {2,6} \right)$. Using the distance formula, we find that the lengths of the diagonals are $\sqrt {{{(9 - 2)}^2} + {{(7 - 6)}^2}} $ and $\sqrt {{{(8 - 3)}^2} + {{(9 - 4)}^2}} $, which both simplify to $\sqrt {50} $.
Are we better off than we were before? Now we know that our conjecture is true for two rectangles, but that still leaves lots of other rectangles we’re not sure about. Another strategy might be to draw a rectangle that could represent any rectangle. To make life easiest, let’s position it so that its bottom edge lines up with the $x$-axis, with its left side touching the origin.
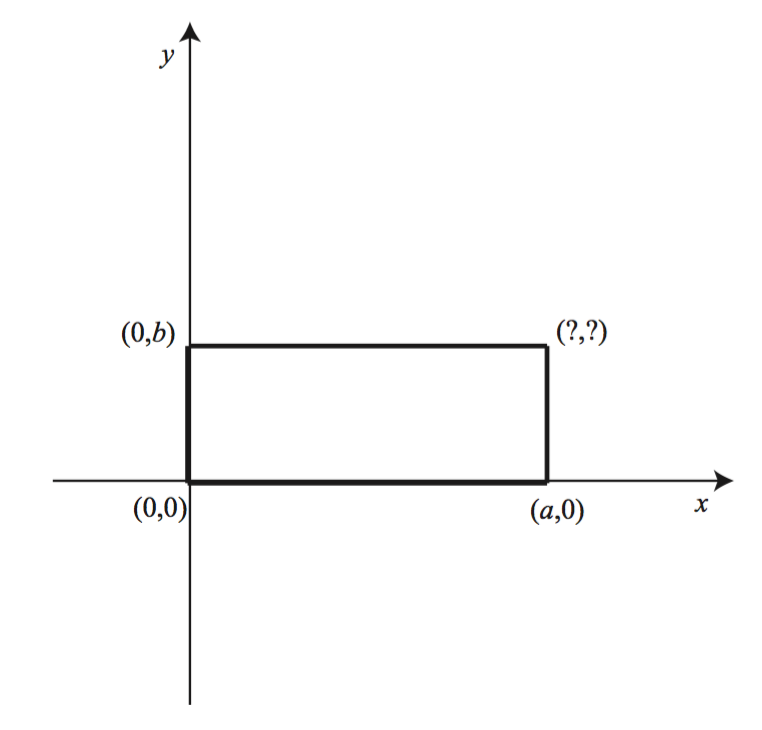
We don’t want to say how long the sides are, because then we’d have a specific rectangle. So let’s just call the lengths $a$ and $b$.
Notice that the coordinates of the point in the rectangle’s upper right corner have been left blank. We could be lazy and fill them in with two more letters: $\left( {c,d} \right)$. But there is a way to do it in terms of the other letters that are already in the diagram.
Read the previous paragraph (if you haven’t already) and find a better way to name the coordinates of the point in the upper right corner.
Now use the distance formula to find the length of each diagonal of this rectangle. Note that your answers will have letters in them that won’t go away! How do your answers compare? What did you just prove?
Using symbols to represent numbers or coordinates that could take on any values is another example of representing symbolically. In addition to allowing us to do the proof, representing the coordinates symbolically has a side benefit here: any calculations we do using these symbols will apply to any rectangle we could possibly come across.
Use the formula you found in Problem 18 to find the lengths of the two diagonals of a 17x42 rectangle. Does your formula work?
Socrates read your work in Problem 18, and complained that you’ve really only shown that the diagonals are congruent for rectangles that have a corner at $\left( {0,0} \right)$ and are sitting flat on the $x$-axis. Is he right? Do you have a response?
Draw a square that can represent any square, placing it on a grid and labeling the coordinates of its important points with letters (as you did in Problem 17). You may want to make one of its corners the origin. Now calculate the length of the diagonals of your square.
Draw an isosceles triangle that can represent any isosceles triangle.
Find two different sensible ways to place your triangle on a coordinate plane. Label the coordinates using a minimum number of letters, as in Problem 17.
Find the coordinates of the midpoint of each of the same-length sides. Now connect each midpoint with the vertex opposite it, as below. Are these two line segments the same length? Prove it for any isosceles triangle.

Part b of the previous problem is a proof of a theorem. State the theorem you proved.
Now rotate your isosceles triangle of Problem 22 so that the base side (the side that is a different length from the other two sides) is vertical. Does your proof apply to triangles like these, as well?
You’ve now had a bit of practice doing proofs that aren’t just about specific diagrams. For example, you proved that the diagonals in ANY rectangle are the same length.
Of course, some statements you’ll investigate in geometry may turn out to be false. When you’re asked to prove something, it’s a good idea to figure out if it’s worth it to even begin the proof — maybe the statement wasn’t true to begin with.
Draw some pictures to decide if it is worth it to prove the statement “the diagonals of a parallelogram are the same length.”
If you can draw a picture that shows a statement must be false, that picture is called a counterexample.
Practice
Draw a parallelogram that can represent any parallelogram, placing it on a grid and labeling its coordinates with letters (as in Problem 17).
Draw an equilateral triangle that can represent any equilateral triangle, labeling the important points as always.
In the previous question, you probably had to use two different letters to label the points. Now find a way to get it down to one letter.
According to your definitions,
Is a square a type of rectangle?
Is an equilateral triangle a type of isosceles triangle?
Is a rhombus a type of parallelogram?
Is a rectangle a type of square?
Is a parallelogram a type of trapezoid?
For a rectangular box with width 4, length 5, and height 6,
What is the exact (i.e. no rounding) length of the diagonal of the base?
What is the exact length of the diagonal that connects opposite corners of the box?
A kite is a quadrilateral that has two pairs of congruent, adjacent sides, as pictured below.

Carefully explain why most parallelograms do $not$ fit the definition of a kite.
Is a rhombus a type of kite?
Problems
Whenever you test a statement in geometry to see if it’s true, you should visualize by drawing several, varied pictures of the shape you’re investigating. If you can’t find a counterexample and the statement appears to be true, it’s time to look for a proof. But it is never good enough to prove something by doing the calculations on a specific shape you drew. You’ll have to represent the coordinates symbolically by using letters that can stand for any number. That way, you’ll be sure your proof works for all shapes. Practice using both of these strategies in the five problems that follow.
Do the non-parallel sides of a trapezoid have to be congruent? Either prove it, or find a counterexample.
Prove that in any triangle the line segment joining the midpoints of any two sides is parallel to the third side.
Prove that in any triangle the length of the line segment joining the midpoints of any two sides is equal to half the length of the third side.
Is it the case that the line segments joining the midpoints of successive sides of a rectangle form a rhombus? Prove it or find a counterexample.
$FAN$ is a right triangle with the right angle at $A$. A line segment is drawn from $A$ to the midpoint $Y$ of $\overline {FN}$. Is the conjecture that $AY = FY$ true? Justify your answer. (Choose your coordinates carefully.)
Recall that a median of a triangle is a line drawn from the vertex to the midpoint of the opposite side.
$A\left( { - 3,13} \right)$, $B\left( {9,1} \right)$ and $C\left( { - 9,1} \right)$ are the vertices of a triangle.
Draw the triangle and its medians $\overline {AD} $, $\overline {BE} $ and $\overline {CF} $ on graph paper.
Find the equations of the three medians.
It appears that the three medians all cross at the point $\left( { - 1,5} \right)$. Is this really true, or are they just close?
What theorem does Problem 38 suggest about the medians of any triangle?
A lattice point is a point where both coordinates are integers, like $(-7,2)$, but not like $(3,5.5)$. Is it possible to form a square whose area is 72 by connecting four lattice points? How about if the sides of the square cannot be horizontal or vertical?
Let $a$ be any number. Is the quadrilateral with vertices $(a,7a),\;(6a,5a),\;(2a, - 7a)$, and $( - 4a, - 5a)$ sometimes, always, or never a rectangle, depending on the value of $a$?
Don’t use a calculator for this problem.
Subtract $7\frac{1}{4} - 3\frac{3}{5}$
Factor ${x^2} - 3x - 54$
Solve for $x$: $\frac{1}{{x + 2}} = 4$
Are the following expressions “negative reciprocals”? $\frac{-6x^2}{-4x}$ vs. $\frac{2}{{3x}}$
Find all values of $x$ where $- x = |x|$.
Is it possible for a line to go through no lattice points? Exactly one lattice point? Exactly two lattice points?
Can both the length and width of a rectangle be irrational and yet the length of its diagonal be an integer?
It’s one thing to prove something that someone else asks you to. But it is often more fun (and what mathematicians actually do) to prove something you thought of yourself. When you come up with a statement you think is true, though you don’t know for sure, that’s called a conjecture. As always, visualizing remains of the utmost importance when coming up with conjectures.
For what kinds of quadrilaterals do the diagonals cut each other exactly in half? Consider squares, rectangles, rhombuses, parallelograms, kites, and trapezoids. Choose one shape for which this is true and write a proof.
For what kinds of quadrilaterals are the diagonals congruent? Consider rhombuses, parallelograms, kites, and trapezoids (since you’ve already considered squares and rectangles). Choose one shape for which this is true and write a proof.
For what kinds of quadrilaterals are the diagonals perpendicular to each other?
On a sheet of graph paper use a straightedge to draw any quadrilateral — the uglier the better. Now, as accurately as you can, find the midpoint of each of the sides and connect those midpoints in order with line segments.
What appears to be true about the new quadrilateral you have drawn?
Have a conversation with your group about the most sensible way to label the coordinates of a quadrilateral that can represent any quadrilateral. Choose wisely, because soon you’re going to…
…prove your conjecture in part a.
Exploring in Depth
$\left( {0,0} \right)$, $\left( {1,4} \right)$, $\left( {3,b} \right)$, and $\left( {c,d} \right)$ are the four vertices of a rhombus. Find values for $b$, $c$, and $d$. Then find at least one other set of values for $b$, $c$, and $d$ that work (draw a picture).
Here is a circle, with a line drawn tangent to it — the line hits the circle in exactly one place. The radius of the circle is also shown. What angle do the tangent and radius appear to form? Prove that they do indeed form this angle.

Two vertices of triangle $ABC$ are located at $A\left( {2,7} \right)$ and $B\left( {-4, 5} \right)$ and the area of the triangle is 8 square units. Write an equation that describes the position of the point $C$.
There is something funny about the pair of pictures below.
Calculate the area of each piece making up the two shapes below. Do the pieces stay consistent in size from the first picture to the second?
Add up the areas of the four pieces making up the shape at the top. This should be the area of the top shape. Then add up the areas of the four pieces making up the shape at the bottom. What does this show about the areas of the top and bottom shapes?
Take another look at the top and bottom shapes. Does it make sense that they would have the same area?
Tinker! There’s more you can calculate in this picture besides just the areas of the various shapes. Get more data and see if you can use it to explain this optical illusion!
