O Bottom! Thou art translated!
–A Midsummer Night’s Dream
Development
Here is a picture of a ghost, whom you might recognize from the video game “Mac-Pan.” The ghost goes through the points $\left( {1,0} \right)$, $\left( {3,2} \right)$, and $\left( {4, - 1} \right)$.
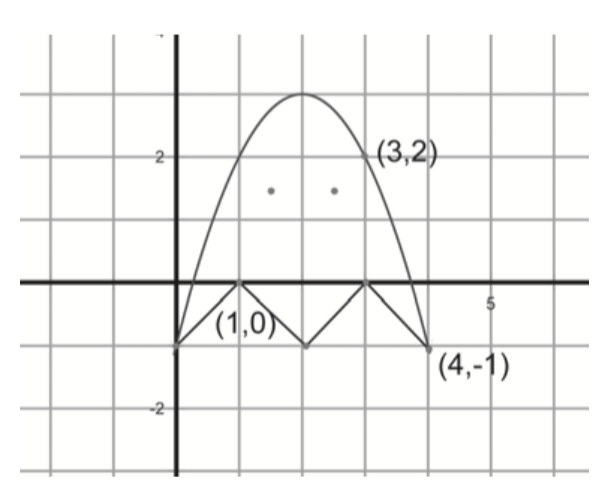
Those annoying ghosts will never stay put. This one moves three units to the right. What will be the new coordinates of the points on the ghost that are labeled in the picture?
Someone programming a computer game would have a hard time giving instructions like this: “If the ghost is at points$\left( {1,0} \right)$, $\left( {3,2} \right)$, and $\left( {4, - 1} \right)$ and needs to move three units to the right, the new coordinates will be…” If they programmed it that way, then if the ghost started in a different position they would have to change the instructions. Instead, the instructions would be more like “If a part of a ghost is at the point $\left( {x,y} \right)$ and the ghost moves three units to the right, that part will land on the point…”
You fill in the rest of the previous sentence. Make sure it works by trying it out on the points $\left( {1,0} \right)$, $\left( {3,2} \right)$, and $\left( {4, - 1} \right)$ and plotting them on a graph.
Now think like a game designer and examine the more general problem. Ghosts can move up and down as well as right and left. Say the ghost’s right eye is at the point $\left( {x,y} \right)$.
What will be the new coordinates of the eye if the ghost moves 5 units to the left?
What if the ghost moves 4 up?
What if 2 down?
What if 3 to the right AND 4 up?
How about 1 to the left AND 6 down?
These movements that the ghost makes are called translations. A translation of a shape changes its position, but doesn’t change anything else about the shape, like the size or the angles. A translation also doesn’t change which way the shape is pointing.
Sometimes a game designer would like to change the way an object is pointing, though. For instance, in the figure below Mr. Mac-Pan is moving to the right, but if he changed direction so that he was moving upwards it might look more realistic if his mouth pointed up instead of to the right. This kind of change in an object is called a rotation.

It’s natural to ask where a point $\left( {x,y} \right)$ would wind up after a certain rotation. The answer might not be obvious, but we can make this question easier for ourselves by thinking about a specific example first.
Rotate Mr. Mac-Pan 90 degrees counterclockwise around the
point
Where does the top of his head (previously at $\left( {0,2} \right)$) land?
Where does his bottom jaw (previously at $\left( {1.5, - 1} \right)$) land?
Where does his “middle” (previously at $\left( {0,0} \right)$) land?
The rotation you did in the previous problem is called a 90-degree rotation with center $\left( {0,0} \right)$. When not specified, it’s assumed the rotation is counterclockwise.
Based on your results in the previous problem, say where a point $\left( {x,y} \right)$ lands after a 90-degree rotation with center $\left( {0,0} \right)$.
Trying specific numbers when you’re asked to solve a more general question is an example of tinkering. When you’re asked to come up with a formula, you can tinker by generating data for yourself. Use tinkering copiously in this lesson.
Where would each of the three specified points (in problem 4) on Mac-Pan land if you instead did a rotation of 180 degrees? How about 270 degrees?
Tinker: Make up some other simple shapes that contain the point $\left( {0,0} \right)$, and rotate them 90, 180, and 270 degrees counterclockwise around the origin. Conjecture two more formulas describing where a point $\left( {x,y} \right)$ will end up — one for the 180-degree and one for the 270-degree rotation. If necessary, cut out each shape and physically spin it.
In problem 4, you rotated Mr. Mac-Pan 90 degrees with center $(0,0)$.
Using the same method as problem 4 — and cutting out a model if necessary — rotate Mr. Mac-Pan 90 degrees with center (0,2).
Where does the top of his head (previously at $\left( {0,2} \right)$) land?
Where does his bottom jaw (previously at $\left( {1.5, - 1} \right)$) land?
Where does his “middle” (previously at $\left( {0,0} \right)$) land?
Another way we could transform an object is through a reflection. Let’s start simply by considering this triangle.

We’re going to draw the mirror image of this triangle, acting as if the $x$-axis were a mirror. Draw the new vertices and label them $A'$, $B'$, and $C'$ to show that they correspond to the points $A$, $B$, and $C$, just as the top of the ghost’s head after a translation corresponds to the top of the head before. Then fill in the rest of the triangle. This is called a reflection over the $x$-axis.
Suppose you wanted to reflect a ghost over the $x$-axis. If a point $\left( {x,y} \right)$ were on the ghost, where would it fall?
What would be the new coordinates of a point $\left( {x,y} \right)$ if it were instead reflected over the $y$-axis?
Another well-known feature of Mac-Pan: when a ghost eats Fattening Fungi, she grows twice as tall and twice as wide.
This ghost is in a corner — a floor and wall formed by the $x$- and $y$-axes. When she expands, her “feet” need to stay on the floor, and she can’t expand past the wall, either, as she’s not your usual ghost. Here’s the ghost:
.png)
Draw in the new ghost, if she still expands to twice her length and width but can’t move through the wall or floor.
Where does the top of her head go?
Where do her leftmost and rightmost bottom corners go?
Are there any points on or in the ghost that wouldn’t move?
If a point $\left( {x,y} \right)$ is on this ghost, where does it go?
Try out your conjecture from the last question. If the ghost’s eyes are at $(\frac{3}{2},\frac{5}{2})$ and$(\frac{5}{2}, \frac{5}{2})$ , use your formula to predict where they’ll go after the ghost eats the fungus. Does that look right in the picture?
This type of change in shape is called a dilation. In this case, it is a dilation of magnitude 2, or a dilation by a factor of 2. And, as with a rotation, the point that doesn’t move is called the center. Even though it is not in the center of the ghost, the point $\left( {0,0} \right)$ is the center of this dilation.
Now suppose that the ghost below can’t move past the ceiling at the line $y = 4$, but she can move past the $x$- and $y$-axes now. If she still expands to twice her length and width, draw in the new, dilated ghost.

Which point in problem 17 stays the same before and after the dilation? What special name does this point have?
Looking again at Problem 11,
What is the distance from the point $\left( {1,1} \right)$ on the original ghost to the center of the dilation?
What is the distance from the image of the point $\left( {1,1} \right)$— the place where that part of the ghost lands after the dilation — to the center of the dilation?
Looking at Problem 17,
What is the distance from the point $\left( {1,1} \right)$ on the original ghost to the center of the dilation?
What is the distance from the image of $\left( {1,1} \right)$ to the center of the dilation?
The observations in the previous problem suggest another way to do dilations, without using coordinates. First, we’ll start with a point not on a grid, and a triangle to dilate. Our goal is to make the triangle twice as big.

Now we’ll make each point on the triangle twice as far away from the center headed in the same direction away. Here’s what that looks like for one of the points on the triangle:

Copy the diagram above into your notebook, and then find the images of the other vertices of the figure. You’ll need to use a ruler to find twice the length.
This, of course, was a dilation of magnitude 2, since all the lengths were doubled.
Make another copy of the diagram preceding problem 21. Then draw the image under a dilation of magnitude 3.
Using the same diagram as in Problem 22, draw the image under a dilation of magnitude $\frac{1}{2}$. Perhapas a better word than "dilation" here would be contraction.
You can think of the lines you’ve drawn in to help draw each image as “guide lines.” Use the guide lines to draw in a few more images of the triangle under dilations or contractions, even though you may not be sure what the scale factor is. What do you have to pay attention to in order to make sure your triangle stays the right shape?
One more bit of vocabulary: When you apply a transformation to a shape, the new figure is called the image of a shape under that transformation. This is kind of like calling what you see in the mirror your image — a shape that is where you’d be if you were reflected over the mirror.
In this section, you have learned about four types of transformations:
Translations move a shape without changing its orientation
.Rotations spin a shape around a certain point.
Reflections give the mirror image of a shape on the other side of a line
Dilations/Contractions stretch a shape away from a point or shrink a shape toward a point, keeping the same proportions as before.
Practice
O student! Thou are also reflected, rotated and dilated!
Say where the point $\left( { - 2,4} \right)$ goes under:
A translation of 3 units to the left and 4 units down.
A dilation by a factor of 2, centered at the origin.
A reflection over the $y$-axis.
A reflection over the line $y = 2$.
A rotation of 180 degrees centered at the origin.
A rotation of 90 degrees centered at $\left( {1,1} \right)$.
Draw a triangle with vertices at $\left( {1,3} \right)$, $\left( {4,10} \right)$, and $\left( {6,5} \right)$. Then apply the following transformations to the triangle. In each case, draw the resulting triangle and give the new coordinates.
A translation of 4 units to the right and 3 units down.
A reflection over the line $x = - 1$.
A dilation by a factor of 3, centered at the origin.
A reflection over the line $y = 3$.
A rotation of 90 degrees centered at $\left( {1,3} \right)$.
On the axes below, draw in the following transformations of Mac-Pan:
Reflection over the $x$-axis.
Reflection over the $y$-axis.
Translation of 5 to the left.
Translation of 6 to the left and 3 down.
Rotation of 90 degrees centered at $\left( {1,3} \right)$.

Draw your own shape on graph paper and give the coordinates of a few key points. Then apply the following transformations to the shape. In each case, draw the resulting shape and give the new coordinates of the key points.
A dilation by a factor of 2, centered at the origin.
A translation of 2 units to the right and 4 units up.
A reflection over the $y$-axis.
A reflection over a line that contains one of the points on your shape.
Where does the point $\left( {x,y} \right)$ end up under a dilation by a factor of 3, centered at the origin?
For each of the shapes and points below, copy them to the middle of a full-sized sheet of paper and then use a ruler or other accurate method to find the dilation or contraction.
Dilation with magnitude 2
Contraction with magnitude ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}$
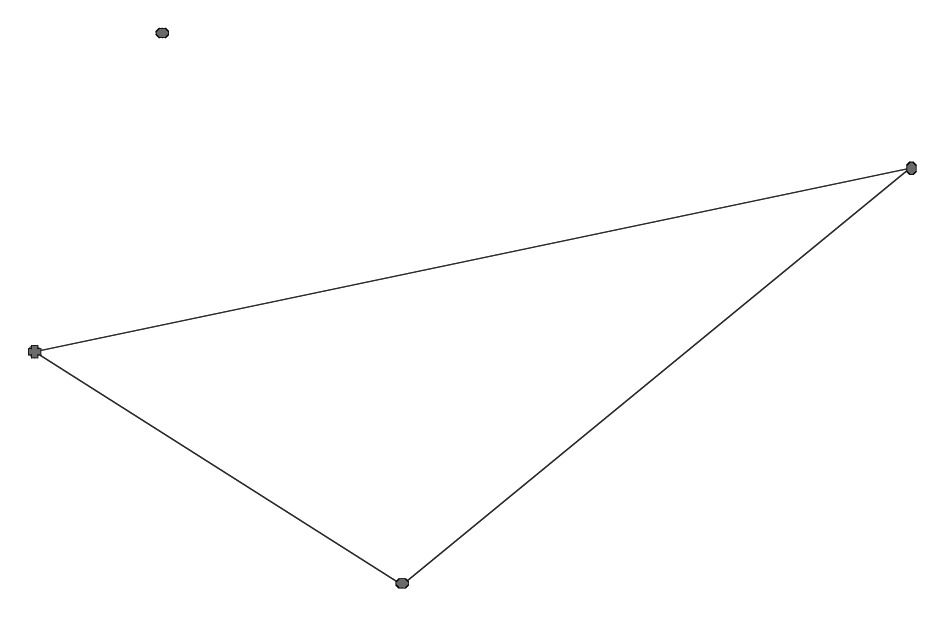
Dilation with magnitude 3
Contraction with magnitude ${\raise0.5ex\hbox{$\scriptstyle 2$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}$
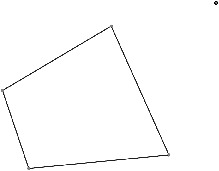
Dilation with magnitude 1.5
Contraction with magnitude ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 3$}}$
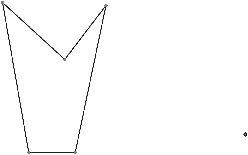
Dilation with magnitude 2
Contraction with magnitude ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}$
Problems
Rotate the following point 90 degrees counterclockwise around the origin. What are its new coordinates?

Rotate this rectangle 90 degrees clockwise around the origin and give its new coordinates.

For each part of this problem, give step-by-step instructions for how to transform the solid shape into the dashed shape. An example of this for the shape below would be 1) Rotate ${90^ \circ }$ counterclockwise around the origin; 2) dilate by a factor of 2 about the origin; 3) Translate 1 unit to the left and 1 unit down.
Figure for the example:






Choose one part of problem 36 and solve it in a different way. See if you can do it with a different group of steps, not just by changing the order of steps in your previous answer.
Make up a problem like Problem 36 and give it to a friend to solve.
What line should you reflect over to get $\left( {1,1} \right)$ to go to $\left( {4,0} \right)$?
Take the point $\left( {9,1} \right)$. Find its image if it is rotated 45 degrees counterclockwise around:
$\left( {11,3} \right)$
$\left( {1,1} \right)$
The following transformations are written on slips of paper and thrown in a hat.
Up 3
Left 4
Dilation of magnitude 2 centered at (0,0)
You draw the three transformations out of a hat without looking, and perform the transformations in the order in which you drew them on the point (0,0). What’s the probability that
(0,0) will land on (-8,6)?
(0,0) will land on (-4,6)?
Don’t use a calculator for this problem.
Which of ${x^2} + 36$ or ${x^2} - 36$ can be factored?
Solve for $x$: $\frac{{1 + x}}{{1 - x}} = 5$
Solve the inequality $|x + 3| < 4$
Find $2.\overline{3} \cdot 6$
If ${x^2} = 25$ but ${x^3} \ne 125$, what is $\frac{1}{x}$?
The function Twist takes a point, rotates it 90 degrees clockwise around the origin, then translates it 2 units to the right, and then finally reflects it over the $x$-axis.
If Twist($P$) = (1,-1), then where is the point $P$?
Make up a function Warp such that Twist(Warp($P$)) = $P$ for any point $P$.
Trace the following dilations onto a clean sheet of paper. Then find the center of each dilation.
.pdf.jpg)
Make sure you have a ruler. In parts a and b of the previous problem, how does the perimeter of the image compare with the perimeter of the original shape? How about the areas? What was the scale factor in these dilations?
A dilation of magnitude 4, centered at $(x,y)$, moves the point (3,4) to the new point (8, -16). What is $(x,y)$?
If a dilation centered at $\left( {1,3} \right)$ takes $\left( {3,10} \right)$ to $\left( {9,b} \right)$, find $b$ and find the factor of dilation.
Consider the points (1, 1) and (1000, 1000).
Which of the two points has a greater percentage increase in distance from the origin when shifted up 4, then dilated with magnitude 2 centered at the origin?
Which of the two points has a greater percentage increase in distance from the origin when first dilated with magnitude 2 centered at the origin, then shifted up 4?
Which point had the greatest percentage difference between the distance it moved in part a and the distance it moved in part b? Why could you have predicted that without doing any calculations?
Often, you know more than you think you know. Problems 49-51 ask you to find formulas for some complicated transformations. You can make them more manageable by first simplifying the problem — asking yourself the same question using numbers for the point instead of $(a,b)$ or $(x,y)$. In some ways, this is the opposite of representing symbolically — you’re moving from general symbols to specific examples. As always, if you’re having trouble figuring out where a point would go, don’t forget to draw a picture.
Describe where the point $\left( {a,b} \right)$ ends up if a shape that contains it is reflected over the $x$-axis, then the result is reflected over the $y$-axis, and then reflected over the $x$-axis again.
Find the new coordinates of a point $\left( {x,y} \right)$ after a dilation of magnitude 3 centered at the origin.
Find the new coordinates of a point $\left( {x,y} \right)$ after a dilation of magnitude 3 centered at $\left( {1,2} \right)$.
Simplifying the problem is particularly useful when asked to come up with a conjecture: a statement which you believe always to be true. The following questions ask you to do that.
The square $\left( {1,0} \right)$, $\left( {5,0} \right)$, $\left( {1,4} \right)$, $\left( {5,4} \right)$ gets stretched vertically so that it still sits on the $x$-axis and becomes a rectangle twice as tall but with the same width.
Give the coordinates for the rectangle.
Conjecture a formula that describes what happens to any point $\left( {x,y} \right)$ under this transformation.
Describe what happens when you try your formula with a shape that’s not sitting on the $x$-axis.
Conjecture a formula that would stretch a shape horizontally to be twice as wide but keep the same height. Your guess should describe what to do to a point $\left( {x,y} \right)$ on the shape to make the stretch.
Although you have studied rotations around the origin of multiples of 90 degrees, other angular rotations are possible — for example, 43 degrees. An angular rotation can be repeatedly applied as well, so two rotations of 43 degrees would be equivalent to a rotation of 86 degrees.
Say you have an asymmetric figure. You repeatedly apply a 240° rotation to it. How many times do you need to apply the rotation before the figure returns to the same position in which it started?
Which angular rotations between 0 and 360 degrees, after being repeatedly applied to a figure, will eventually result in the figure returning to its starting position?
Are there repeated angular rotations that do NOT eventually result in the figure returning to its original position? If so, what do these angles have in common, and if not, try to prove that any angular rotation will eventually return a shape to its starting position if repeated enough times.
Exploring in Depth
In Problem 43, Warp is called the inverse function of the function Twist. Explain this terminology.
Find a formula for reflecting the point $\left( {x,y} \right)$ over the line $y = 3$. Then for the line $x = - 2$.
Try the formulas you found in problems 5 and 6 on some shapes that do not contain $\left( {0,0} \right)$. Describe what you see. Do you think that what is happening still deserves the name "rotation around $\left( {0,0} \right)$”?
Below is Mac-Pan. When he moves around the screen, his mouth always points in whichever direction he is moving. If you’ve done the previous problem, you realize that a game designer cannot accomplish this just by telling Mac-Pan to rotate ${90^ \circ }$ every time he changes direction. What should you do to fix this problem?
Prove that parallel lines stay parallel after a dilation centered at the origin.
If you draw any isosceles triangle on the plane, and then do a horizontal stretch (as in Problem 53), will it still be isosceles?
Take the point $\left( {6,1} \right)$ and rotate it 45 degrees counterclockwise around $\left( {2,5} \right)$. What is its image?
We still don’t have a formula that will allow you to figure out the image of a dilation centered at a point. The following few problems will help you derive it. Let’s start just by thinking about dilating any shape around the point $\left( {3,2} \right)$. Then we’ll start to use symbols, one piece at a time.
In the $x$-direction, how far is the point $\left( {x,y} \right)$ from $\left( {3,2} \right)$? Your answer should be a signed distance — that is, if your point is to the right of $\left( {3,2} \right)$ the distance is positive and if your point is to the left of $\left( {3,2} \right)$ the distance is negative.
In the $y$-direction, how far is $\left( {x,y} \right)$ from $\left( {3,2} \right)$?
If $(x', y')$ is twice as far as $\left( {x,y} \right)$ from $\left( {3,2} \right)$, how far away is it in the $x$-direction? In the $y$-direction? Make sure your answer is in terms of $x$ and $y$, not $x'$ and $y'$.
Now write a formula that gives the $x$ and $y$ coordinates of $(x', y')$ in terms of the coordinates $x$ and $y$.
Test your formula on some specific points. Make sure that they wind up twice as far away from $\left( {3,2} \right)$ after the dilation. If not, go back and change your answers to the previous questions until you find a formula that works.
Now adapt your formula so that it works not just for a dilation by a factor of 2, but a dilation by a factor of $n$.
Finally, adapt your formula so that it works not just for a dilation centered at $\left( {3,2} \right)$, but one centered at the point $\left( {h,k} \right)$.
Below is that ghost again, so familiar from the beginning of this lesson.

Write a formula for dilating her around her right “foot” (at $\left( {4, - 1} \right)$). Say you want her to grow by magnitude 2.
Write a formula for contracting her with magnitude ${\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}$ with center $\left( {6,4} \right)$.
Write a formula for dilating her with magnitude 1.5 with center $\left( -1,-2 \right)$.
Copy the ghost onto a large piece of graph paper, and then use your formulas to draw sketches of her after each of the three transformations.