Do the indicated operation and write your final answer as a single fraction. Do not use the fraction capabilities of your calculator.
$\frac{3}{4} + \frac{5}{9}$
$\frac{5}{7} - \frac{5}{{14}}$
$\frac{6}{12}\cdot\frac{-5}{12}$
$\frac{{11}}{3} \div \frac{5}{6}$
$\frac{{\left( {{\textstyle{3 \over 4}}} \right)}}{{\left( {{\textstyle{8 \over 5}}} \right)}}$
Solve each equation below for the indicated unknown.
For $x$: $3x - 8 = 11$
For $y$: $5y + 7 = 3y - 17$
For $a$: $\frac{a}{6} + 3 = 11$
For $b$: $\frac{{b + 3}}{6} = b - 2$
For $y$: $x = -3y + 5$
Solve each of the following equations or inequalities. Do not approximate and show your work.
$5y - 12 = - 4y + 30$
$3\left( {3x - 5} \right) + 4\left( {1 - 2x} \right) = 10$
$\frac{w}{5} + 5 = 2w$
$2\left( {a - 5} \right) \le 6a + 20$
Jillian is a huge fan of Brazilian cheese; so much so, in fact, that she joins a Brazilian cheese eating club where she can get a discount on buying it. Every time she orders it costs 36 cents an ounce plus a 2 dollar shipping charge.
If she bought 5 ounces, how much will she have to pay?
What about if she bought 3.5 ounces? (Assume that fractions of an ounce cost proportionally — e.g. ¼ of an ounce costs ¼ of 36 cents = 9 cents)
If she bought \$5.24, how many ounces did she buy?
If she bought \$7.48, how many ounces did she buy?
Write an equation for $P$, the price Jillian paid, in terms of C, the amount of cheese Jillian ordered, in ounces.
Write an equation for $C$, the amount of cheese Jillian ordered, in terms of $P$, the price Jillian paid.
Consider the following graph.
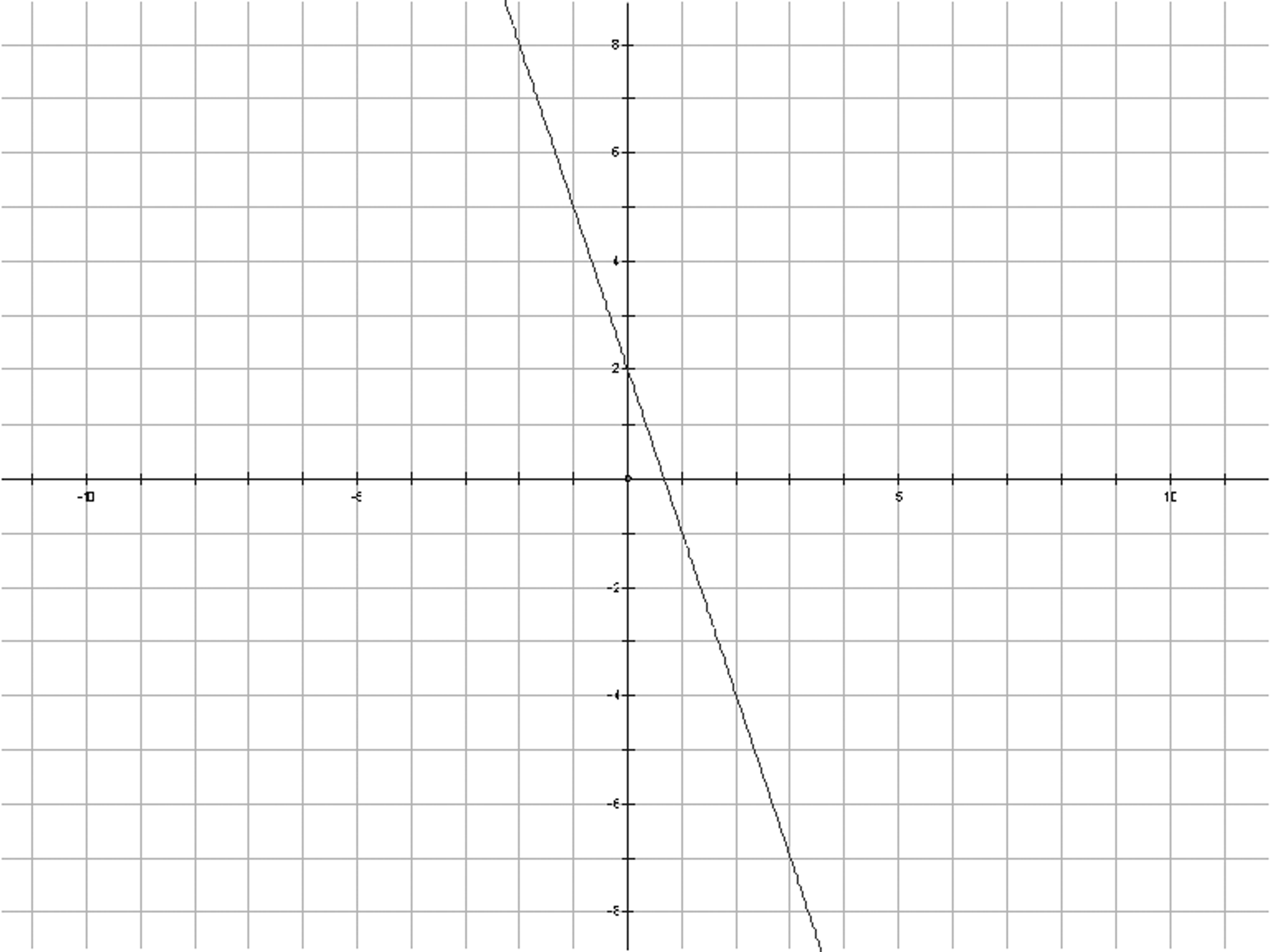
In the graph above, each small square
represents one unit. What is the
Use the graph and the slope to determine what $y$ is when $x$ is 2, and what $x$ is when $y$ is -5.5.
Estimate, using the graph only, what $y$ is when $x$ is 2.7. Then figure out another method where you can determine the answer exactly.
Estimate, using the graph only, what $x$ is when $y$ is 4.2. Then figure out another method where you can determine the answer exactly.
Jasper thinks an equation of this line is $21x + 7y = 14$ . Is he right?
The more students that visit the school store, the fewer super-cool rainbow pens they have. Although not every student that visits the store buys a pen, it is still true that the relationship between students and pens remaining is linear. We are told that after stocking the pens for 8 days, the store has 527 pens remaining, and that after 20 days, they have 323 pens.
How many pens are there left after 31 days?
Determine the $x$-intercept and
What is the equation of the line?
The point $( - 3, - 4)$ is on a line with a slope of $\frac{{ - 7}}{5}$.
What is the equation of the line?
What is the value of $y$, when $x = 12$? When $x = 17.2$?
What is the value of $x$, when $y = 24$? When $y = -16.7$?
Is $(9.2,-21)$ on the graph? Explain.
Write the equation of the line in the form $Ax + By = C$ , where $A$, $B$, and $C$ are integers.
Graph the equation.
Looking at two lines, you see that (5,2) is on both lines.
The $y$-intercept of the first line is $-8$. What is the equation of the line?
The slope of the second line is $-6$ and goes through $(p,-12)$. What is $p$?
State the equations of 2 lines that go through $(-7,13)$, one of which does not have a $y$-intercept, and the other which does not have an $x$-intercept.
The slope from $(Q,2Q)$ to $(4,7)$ is 3. Find $Q$.
Solve the following:
$4(x - 3) - 7 = - 2(6 - x) + 5$
$2x - 5(3 - x) > 17 - (3 - x) - 2(x + 6)$
$\frac{3}{7}x - \frac{2}{5} > \frac{4}{9} - \frac{8}{7}x$
Graph $5x - 4y \le 10$ . (Try using the $x$ and $y$ intercepts as the two points you use to draw the line — it’s quicker!) When $x = - 3$ , what values of y satisfy the inequality?
Graph $ - 2x + 16 = 24$ in 1 dimension AND in 2 dimensions.
If two linear inequalities are graphed on the same axes, and the lines that define them are NOT parallel, is it still possible that there are points in the plane that satisfy NEITHER of the inequalities? Give an example.
Imagine that in the graph below the region to the LEFT of the line is shaded, but that the line itself is dotted. Write an inequality to describe this region.
Let $A = \left( { - 1,7} \right)$ and $B = \left( {4,29} \right)$.
Determine an equation for the straight line passing through $A$ and $B$.
What are the coordinates of the midpoint of the line segment $AB$?
There is a line that is perpendicular to the line segment $AB$ and that goes through the midpoint of line segment $AB$. Determine the coordinates of a point on this line other than the point you found in Part b.
Call the point you found in Part c point $D$. If you connect points $A$, $B$, and $D$ with straight line segments, you will get a triangle. Is this triangle isosceles? How do you know?
List 5 solutions to the equation $4x + 6y = 24$.
List 5 solutions to the inequality $4x + 6y \ge 24$. None of these solutions can be a solution you found in the previous problem.
Find a solution to $4x + 6y \ge 24$ that is not a solution to $4x + 6y > 24$ . Now, show all of the solutions to $4x + 6y \ge 24$ that are not solutions to $4x + 6y > 24$ .
Let $A = \left( {1,4} \right)$, $B = \left( {12,3} \right)$, and $C = \left( {11, - 8} \right)$.
Is the triangle determined by the points $A$, $B$, and $C$ a right triangle? Use mathematics to justify your claim.
Is the triangle determined by points $A$, $B$, and $C$ an isosceles triangle? Recall that an isosceles triangle is a triangle that has two equal sides. Use mathematics to justify your claim.
Write an equation for the line segment that runs from point $B$ to the midpoint of side $AC$.
What special relationship(s) does the line segment you determined in Part C have to side $AC$? Use mathematics to justify your claim(s).
Let $P = \left( {7,13} \right)$ and $Q = \left( { - 8,45} \right)$.
Find $b$ if $(b, -51)$ is on the straight line containing $P$ and $Q$.
Find $c$ if $P$ is the midpoint of the line segment determined by $\left( {22,c} \right)$ and $Q$.
List four solutions to $-3x + 4y = 12$.
Show all the solutions to the equation given in the previous problem.
List four solutions to $-3x + 4y \gt 12$.
Show all the solutions to the inequality given in the previous problem.
Show all of the solutions to $2x - 5y \le 20$.
The following four lines enclose a certain shape. Use algebra to find the vertices of the shape, then prove that the shape is what you think it is.
- $3x - 4y = - 8$
- $x = 0$
- $3x - 4y = 12$
- $x = 4$
The following three lines enclose a triangle. Use algebra to find the vertices of the triangle, then find the area of the triangle.
- $y = - 1$
- $y - 2x = 3$
- $x + y = 6$
Prove that two medians of an isosceles triangle are the same length. (Choose coordinates wisely.)
Do some tests to decide whether the quadrilateral with vertices $(32,50)$, $(75,71)$, $(96,30)$, and $(53,7)$ is a square. If it is a square, prove it. If it’s not, change one of the vertices so that it is now a square.
Given points $P(-1,-1)$, $Q(2,3)$, $A(1,2)$, and $B(7,k)$.
Choose a value of $k$ that makes line $AB$ parallel to line $PQ$.
Choose another value of $k$ that would make line $AB$ perpendicular to line $PQ$.
An altitude of a triangle is a line segment drawn from a vertex of a triangle so that it makes a 90-degree angle with the opposite side. (An altitude is sometimes called the height of a triangle.) Since each triangle has three vertices, each triangle also has three altitudes.
Find equations for all three altitudes of the triangle with vertices $A(-2,9)$, $B(1,1)$, and $C(4,7)$.
Describe a strategy for algebraically showing that the three altitudes of this triangle meet in one point.
Carry out your strategy. At what point do the three altitudes meet?
Let triangle $XYZ$ have its vertices (corners) at $X = \left( {1,2} \right)$, $Y = \left( {4,4} \right)$, and $Z = \left( {2,7} \right)$.
Sketch triangle $XYZ$ on a piece of graph paper. Scale the $x$-axis from $-5$ to $15$ and the $y$-axis from $-5$ to $25$.
Suppose you translate triangle $XYZ$ 4 units to the right and 3 units down. What will be the new coordinates of $Y$?
Suppose you translate the triangle $XYZ$ $h$ units to the right and $k$ units down. What will be the new coordinates of $Z$?
Suppose you used the formula on $(3x, 3y)$ each point of triangle $XYZ$ in order to get a new triangle. Draw this new triangle on the graph in Part a.
How do the two triangles relate to each other? Use mathematics to justify your claim.
Use a straight edge the draw a line through $X$ and its corresponding point on the larger triangle (i.e., on the “$X$” of the new triangle). Extend this line well beyond both of these points. Draw this line as carefully as you can.
Repeat Part f for points $Y$ and $Z$, and their respective corresponding points on the new triangle.
The three lines you drew in Parts f and g appear to have a common intersection point. Where is this? Label this point $P$.
Calculate the distance from $P$ to $X$. Now calculate the distance from $P$ to the point on the bigger triangle that corresponds to $X$. One distance should be longer than the other. By how many times is it longer? Two? Three? Four? Three and a half? Hmmm …
Consider the points $A(-2, 5)$ and $B(8, 1)$.
What is the equation of the line connecting these points?
What is the midpoint of the line segment $AB$?
What is the slope of a line that is perpendicular to $AB$?
What is the equation of the line that is perpendicular to $AB$ and that goes through the midpoint of $AB$? What quadrants does it go through?
What is the distance between $A$ and $B$?
Triangle $ABC$ is a right triangle. Find coordinates for point $C$ (there is more than one answer to this question).
Line $Q$ is parallel to $y = - 3x - 7.8$. Line $Q$ contains the points $(4,18)$, $(6,a)$, and $(b,10)$. Find $a$ and $b$.
2 bugs start at the point (3, 5). One bug travels with a slope of -2.5, and another takes a perpendicular path. Assuming both bugs eventually cross the $x$-axis (let’s call the 2 points of crossing $A$ and $B$), what is the midpoint of $AB$?
C(9, 14) is the midpoint of $AB$. $A$ is (-7, -13).
What are the coordinates of $B$?
$D$ is twice as far away from $A$ as $B$ is, but is closer to $A$ than $B$. What are the coordinates of $D$ (assume $D$ is on the same line as $A$ and $B$)?
The point $\left(x, 0\right)$ is on the line that has -3 times the slope of $AB$ and goes through $D$. Find $x$.
For each of the following, you are given the coordinates of a 3 or 4 sided polygon. Determine as precisely and specifically as possible the nature of the polygon. Support all your assertions with calculations.
(-8,5), (-4,2), (2,11), (-2,14)
(4,3), (8,-5), (12,7)
(0, 0), (5, 5), (15, 5), (7, -1)
The points (2, 1) and (4, 7) are two vertices of a quadrilateral.
Find two other vertices such that the quadrilateral formed by the 4 points is a parallelogram.
Alternatively, find two other vertices such that the quadrilateral formed by the 4 points is a rhombus.
Zimbo made the following claim: “In any triangle, if you draw the segment connecting the midpoints of two sides of a triangle, then the length of that segment is half the length of the third side of the triangle”. Create your own triangle on the coordinate axes and support or refute Zimbo’s claim.
Quadrilateral PROM has vertices P (1, 3), R (4, 7), O (8, 4) and M (9,-3).
Alice claims that PROM is just an ordinary quadrilateral; John claims that it is a trapezoid; Trey claims that it is a trapezoid with a right angle, while Billy claims that it is a trapezoid with two right angles. Take a position and justify it.
For each of the following say whether it be true or false.
Triangle $PQR$ has a right angle at $Q$. If $PR$ = 17 cm and $QR$ = 15 cm, then $PQ$ = 8 cm.
If a line has equation, $y = a + bx$, then its slope is $b$.
The slope of a line joining the points $(a, b)$ and $(c, d)$ is $\frac{(b – d)}{(a – c)}$.
If a line has equation, $y = 2 - 3x$, then any line perpendicular to it will have slope 1/3.
The distance between the points $(1, -2)$ and $(16, -10)$ is 17.
The coordinates of the midpoint of the line segment joining the points $(2a, 3b)$ and $(10a, -7b)$ is $(6a, -2b)$.
A square is a rectangle.
A right triangle may be equilateral.
On graph paper, draw triangle $ABC$
Translated triangle $ABC$ 1 unit to the right and down 2 units, and then reflected it across the $x$-axis.
Reflected triangle $ABC$ across the
Translated triangle $ABC$ 4 units left and 5 units down, reflected it across the $x$-axis, and then rotated it 180 degrees around the origin.
Dilated triangle $ABC$ by a factor of 2, centered at the origin.
Contract triangle $ABC$ by a factor
of
Dilated triangle $ABC$ by a factor of 2, centered at (-1, -2).
Reflected triangle $ABC$ across
the
A flag is drawn below which you should use to answer the following questions.
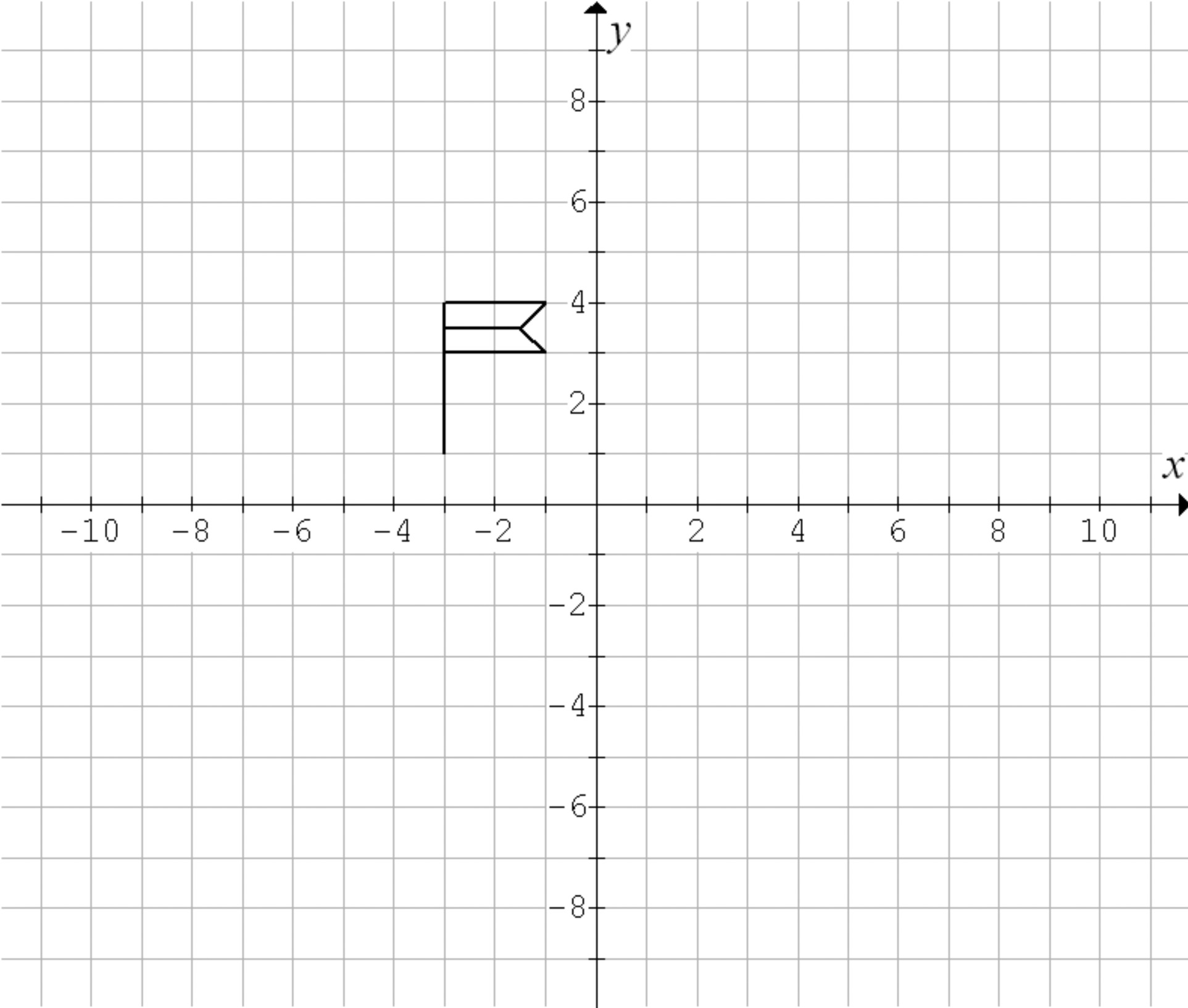
Sketch the resulting shape if the flag is transformed by translating it 2 units left, then rotating it 90 degrees counterclockwise around the origin, and, finally, dilating it by a factor of 2, where the center of the dilation is at $\left( {0,0} \right)$.
Sketch the resulting shape if the
flag is transformed by reflecting it across the y-axis, then
contracting it by a factor of
Sketch the resulting shape if the flag is transformed by dilating it by a factor of 1.5, where the center of the dilation is $\left( { - 4,3} \right)$.
The top left corner of the flag has coordinates $\left( { - 3,4} \right)$ . What should be the exact coordinates of the top left corner of the flag you drew in Part c? Prove that your assertion is true.
We know that if we translate an object two units to the right and then three units down the resulting image will be exactly the same as the result of translating the object three units down first then two units right. In other words, we are confident that horizontal and vertical translations are commutative (the order in which things are done doesn’t matter). Are horizontal translations commutative with any other transformations that we have studied? For instance, are horizontal translations and dilations centered at the origin commutative? Investigate this and other possible combinations and determine which transformations, if any, are commutative with horizontal translations.
Shape $A$ has been dilated by a scale factor $k$ and the resulting image has been drawn. Determine both the location of the center of the dilation and the scale factor $k$.

Rectangle $ABCD$ has point $A$ at $\left( { - 15,86} \right)$ and point $B$ at $\left(31,11\right)$. Determine coordinates for point $C$ and for point $D$. Prove that your $ABCD$ shape is, in fact, a rectangle.
On a coordinate axis system draw a quadrilateral (4-sided figure) which is not a special four-sided figure (for example, it’s not a parallelogram). Identify the exact coordinates of the corners of this 4-sided figure.
Now, determine the exact coordinates of the midpoints of each side of your four-sided figure.
Connect the midpoints in order so that you get another four-sided figure. What type of figure does this appear to be? Prove your assertion.
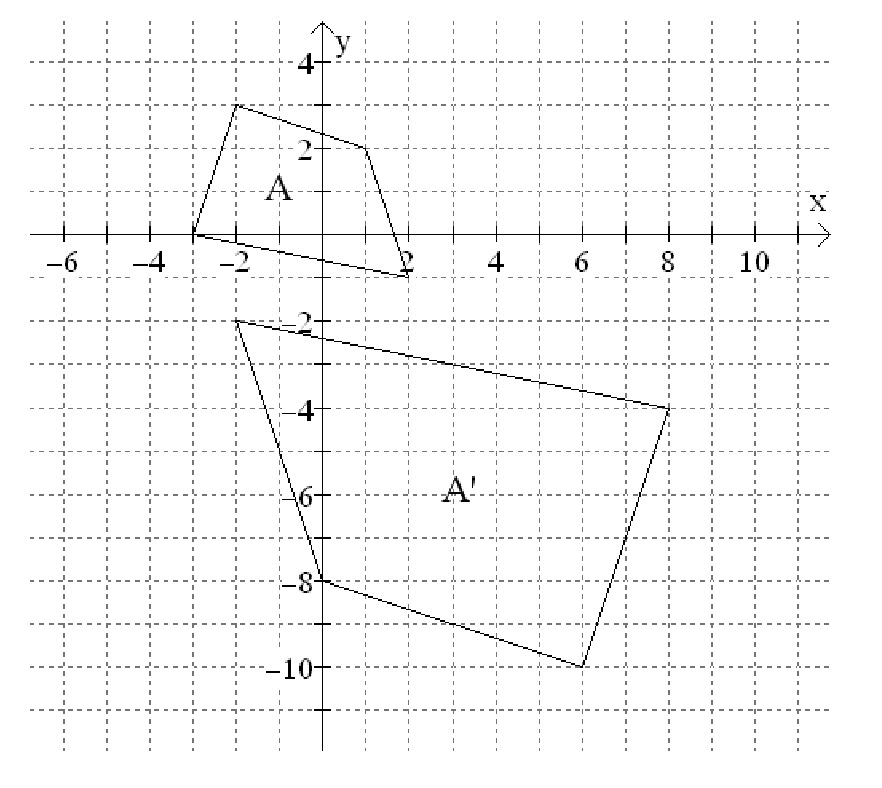
List step-by-step instructions for how to transform shape A into its image A’.

On the axes below, draw the reflection of triangle B over the line $y = x$ .

The reflection of the point $\left( { - 2,4} \right)$ over the line $y = x$ has coordinates $\left( {4, - 2} \right)$ . Check and make sure that this is correct. Now, what is the special relationship between the line that connects $\left( { - 2,4} \right)$ to $\left( {4, - 2} \right)$ and the line $y = x$ ? Prove this special relationship.
The point $(-3,5)$ is rotated $90^{\circ}$ counterclockwise around $(-6,1)$. What are the coordinates of the resulting point? What are the coordinates of the resulting point if $(a,b)$ is rotated $90^{\circ}$ counterclockwise around $(-6,1)$?
The midpoint of line segment AB is $\left( {4,6} \right)$. If point $A$ has coordinates $\left( {8,0} \right)$ , then what are the coordinates of point $B$? Prove that your answer is correct. Note: your proof must show that $A$, $B$, and the given midpoint are on the same line and that the midpoint is the “middle” point of line segment $AB$.
The line segment $XY$ has endpoints $X\left( {4,11} \right)$ and $Y\left( {-3,-3} \right)$. Line $p$ is the perpendicular bisector of line segment $XY$ — that is, it is the line that is perpendicular to line segment $XY$ and bisects the line segment into two equal halves.
What point of line segment $XY$ should line $p$ go through? What are its coordinates?
What should be the slope of line $p$?
Determine the coordinates of a point on line $p$ other than that point which is already on line segment $XY$.
Calculate the distance from the point you found in Part c to point $X$. Now calculate the distance from the point you found in Part c to point $Y$. Notice anything? Hmmm…
List step-by-step instructions for how to transform shape A into its image A’.
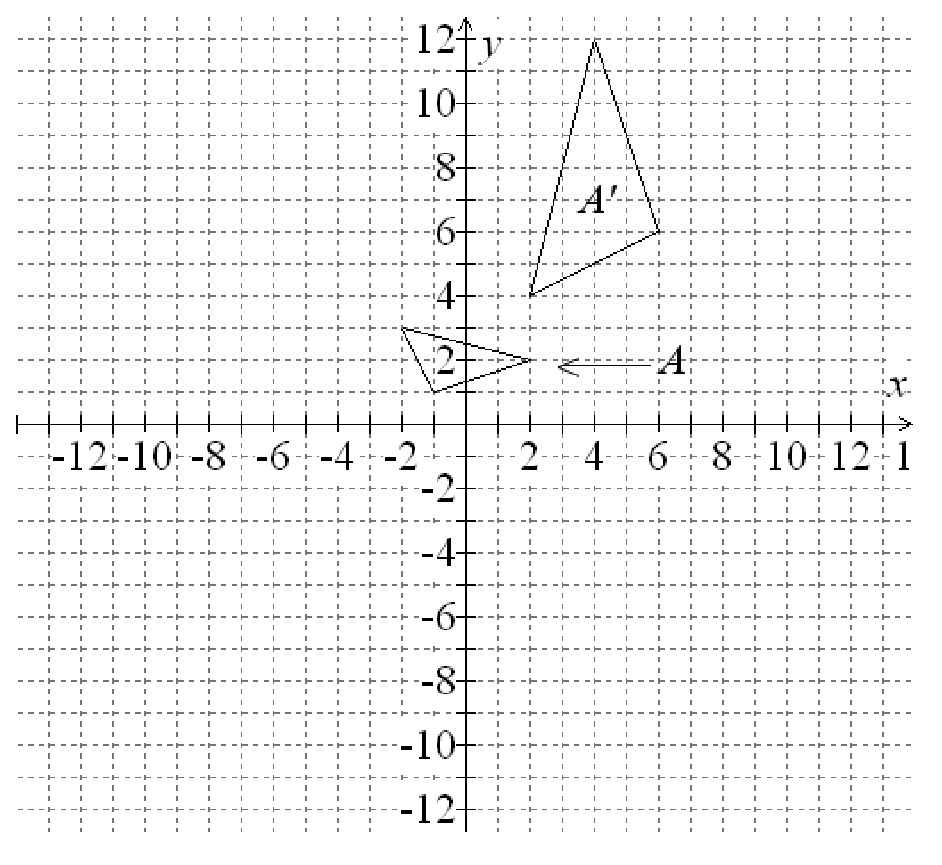

Look back at part a of the previous problem. Come up with a set of instructions for transforming shape A’ into shape A.
Determine the coordinates of the point $P\left( {2, - 3} \right)$ after it is dilated by a factor of 2.5 around the center $\left( { - 1,1} \right)$.
$\left( { - 4,6} \right)$ is the reflection of $\left( {2,0} \right)$ over a straight line. Find an equation for that line.
Let $\left( {2,3} \right)$ be the center point for a ${180^ \circ }$ counter-clockwise rotation transformation. Determine the coordinates of each of the following points under this transformation.
$\left( {4,6} \right)$
$\left( { - 1,8} \right)$
$\left( {5, - 2} \right)$
$\left( {a,b} \right)$
Shape A in Problem 49 Part a is not a right triangle. Show why it is not. What transformation, if any, might turn it into a right triangle?
Shown below is a quadrilateral (a four- sided polygon) that is a parallelogram. Recall that a parallelogram has two pairs of parallel sides.

Show that the figure is indeed a parallelogram.
There is a point around which you can rotate this figure ${180^ \circ }$ counter-clockwise so that the result lands in exactly the same place. What is this point?
Imagine trying to transform the figure so that the result lands on itself, but you can’t use a rotation. Is this possible? If so, how? The transformation does not have to occur in one step and it can’t be trivial — e.g., translate it 2 right then 2 left.
A dilation centered at $(-3, 5)$ takes the point $(1, 3)$ to $(9, y)$. Find $y$ AND the factor of dilation.
A dilation of factor F, centered at point $(x, y)$, takes $(-2, 3)$ to $(-6, -5)$.
Find values of $F$, $x$, and $y$ that make the statement true.
Give a detailed procedure of how you could find an infinite number of different answers to part a.
If the point $(x, y)$ is dilated by a factor of $n$ around the point $(h, k)$, what are its new coordinates? Can you explain WHY the different parts of this formula make sense? Dilate $(5, -2)$ by a factor of 3 around $(-1, 4)$ two ways: 1) by drawing it on graph paper, and 2) by using the formula. Do they give the same answer?