Introduction
Thales of Miletus (625-547 B.C.) is generally regarded as the first of the Seven Wise Men of antiquity. Among other things, he is known for having calculated the height of the Great Pyramid in Egypt using the length of its shadow when compared to a stick in the ground and its shadow at the same time of the day.


Inspired by Thales’ method, Robert and Mary calculated the height of a tree. At a certain time of day, Robert stood at a point such that the tip of his shadow coincided with the tip of the tree’s shadow. Then they measured both the shadow of Robert, who is 1.8 m tall, and the shadow of the tree. They found that Robert’s shadow was 4.32 m and the tree’s shadow was 18 m long. With this information they were able to calculate the height of the tree to be 7.5 m. Could you explain how they might have found the height of the tree?

Taking things apart in the figure in Problem 1, we have two triangles. One right triangle whose legs are the tree and its shadow, and another right triangle whose legs are Robert and his shadow (see figure below). What can you conjecture about the angles in these two triangles? Explain your answer.

Development
Kristi is sitting in the back seat of her parents’ car,
driving from Omaha, NE to visit her grandparents in
Hastings.
The scale on her map is
When leaving her parents’ garage, Kristi first opens the map, she notices that there are about five gum wrapper lengths from Omaha to Hastings. How many miles will her trip be?
How many “gum wrapper lengths” will Kristi measure between her position on the map and Hastings if she is 100 miles away from Hastings?
Much later in the trip, Kristi notices that the distance remaining on the map is about a third of a gum wrapper. How many miles are remaining?
In Baltimore, Maryland, Union Memorial Hospital is the largest building in the triangular region bounded by E University Pkwy, N Calvert St, and E 33rd St (the higher on the map below). If the Union Memorial Hospital’s left side, the side on N Calvert St, is 250 meters long, use the map below to estimate the other two side lengths of this triangular region. You can either measure with a ruler or measure with some other object, like Kristi.

In Middle School, you may have learned how to scale down (or up) a figure. In fact, you may now realize that in doing dilations or contractions, you are changing the scale of a figure. When you scale a figure by a factor of $r$, your new figure will have lengths $r$ times the corresponding lengths of the original figure. This can also be expressed by saying that the sides of the second figure are proportional to the corresponding sides of the first figure by a factor of $r$. In this case, we say as well that the second figure is a scaled copy of the first figure by a factor of $r$.
Below there are some pairs of figures. In Part b, the segments in each figure are perpendicular. Determine whether or not one is a scaled copy of the other. Explain.
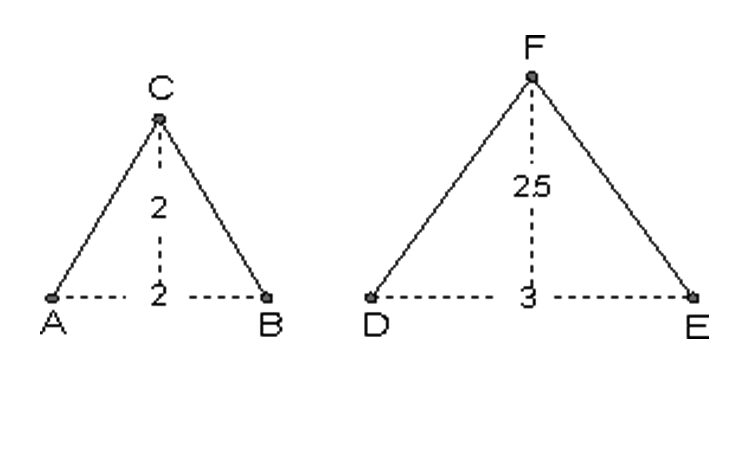

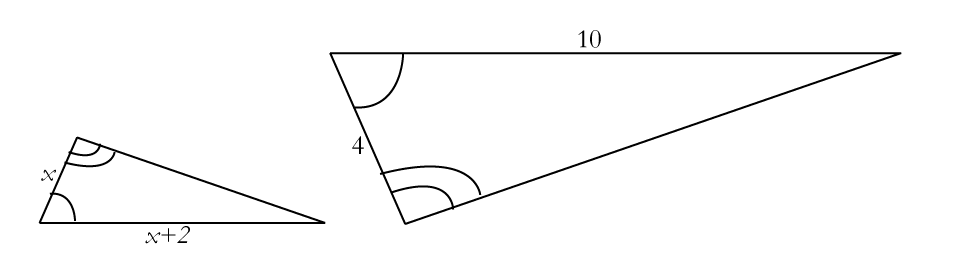
Two triangles are given in the picture below.

Take whatever measurements and do whatever calculations are necessary to check whether or not the two triangles are scaled copies of each other. If they are, determine the scale factor.
Determine the coordinates of the triangle $\triangle A'B'C'$ obtained when you translate triangle $\triangle ABC$ 1 unit down.
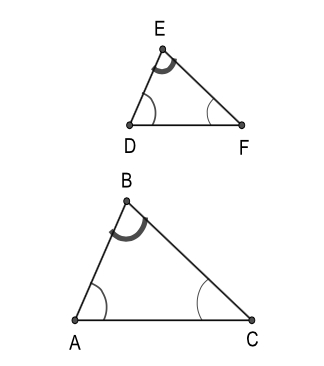
Based on your answer to Question (b), what can you conclude about $\angle B$ and $\angle E$?
What can you say about the two other pairs of angles $\angle A$ and $\angle D$, and $\angle C$ and $\angle F$? Explain.
Triangle $\triangle DEF$ is the image of under a dilation centered at the origin $O\left( {0,0} \right)$.

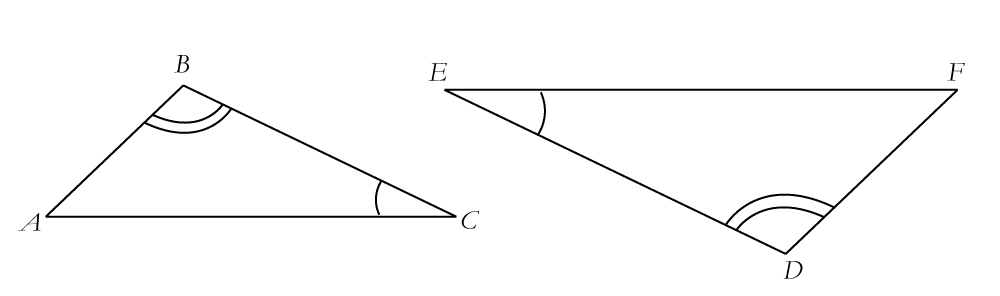
Are triangles $\triangle ABC$ and $\triangle DEF$ scaled copies of each other? If so, what is the scale factor? Explain.
How are the angles of triangle $\triangle ABC$
related to the angles of
In our study of dilations, you may have noticed that the angles of the image of a figure under a dilation have the same measurements as the corresponding angles of the original figure. What’s more, you can see in Problem 7 that the following relationship holds:
side length of image = (scale factor) $\cdot$ (side length of corresponding side in original figure)
The next two problems use the important vocabulary word congruent. Two angles are congruent if they have the same measure, just as two line segments are congruent if they have the same length.
Discuss the following statement with the members of your group.
“If the three angles of a triangle are congruent to the three angles of a second triangle, then the triangles are scaled copies of each other.”
If you disagree, give a counterexample showing that this statement is false.
Now examine the following statement.
“If two angles of a triangle are congruent to two angles of another triangle, then the triangles are scaled copies of each other.”
If you disagree, give a counterexample showing that this statement is false.
The word similar is used in mathematics to describe two triangles that are scaled copies of each other. Similarity plays an important role in the design of large or small objects such as automobiles, airplanes, or integrated circuits. As a matter of fact, before building an automobile, engineers sketch out scale drawings and use them to build scale models which they then use to run tests. Also, as we saw in the introduction of this section, Thales of Miletus may have used similar triangles to calculate the height of the Great Pyramid in Egypt, more than 2500 years ago. Similarity is thus a mathematical instrument that allows us to zoom in or zoom out when examining the physical world.
Thus far, you have discovered several features of similar triangles.
Why does it make sense to use the word “similar” to describe two triangles that are scaled copies of each other?
If two triangles are similar, how are their angles related? How are their sides related?
If you are given a $\triangle ABC$, describe a procedure for drawing a $\triangle A'B'C'$ similar to it.
Practice
In many of the problems that follow, you will see a convention that will be used throughout your high school career. If two angles are marked with arcs that are the same style (both bold, or double instead of single), that means those angles are congruent.
Calculate the lengths of the sides marked by small letters. Angles marked equally have the same angle measurement.
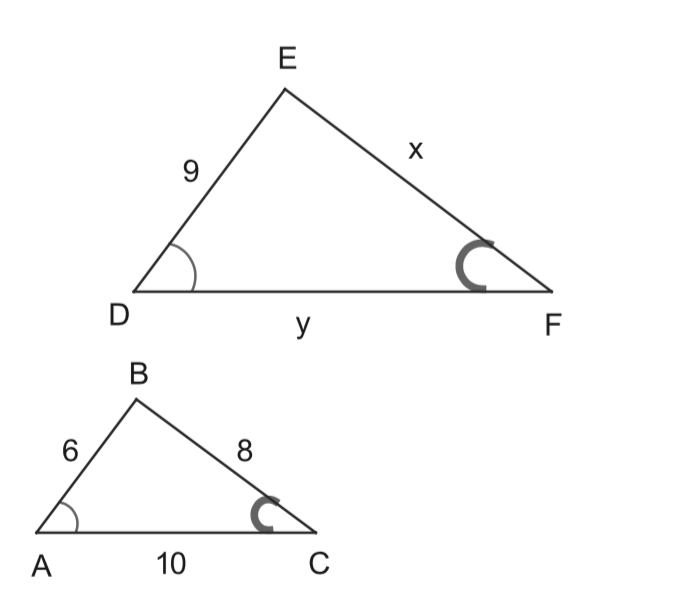
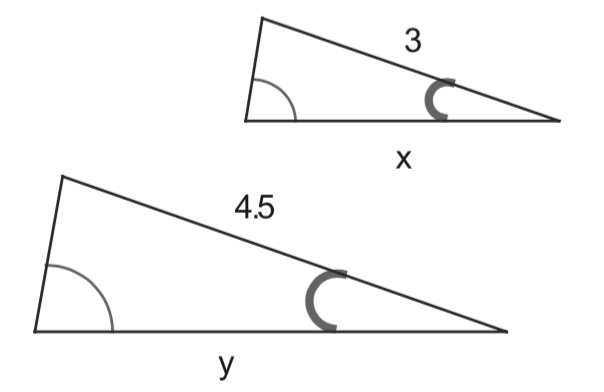
Calculate $x$ and $y$.
Calculate $q$.

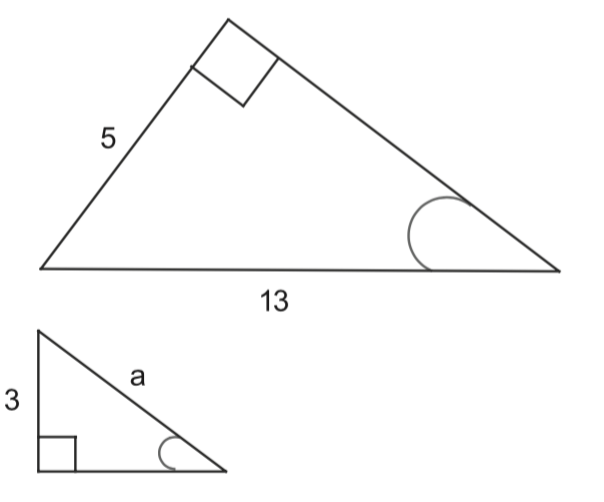
Calculate $a$.
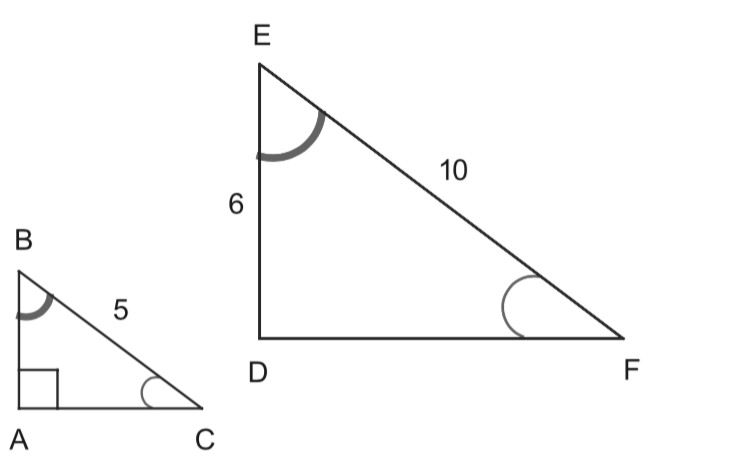
Calculate $h$.

In the figure below, angles marked equally have the same angle measurement.
Find the perimeter of triangle $\triangle ABC$.
Triangle $\triangle DEF$ is a scaled copy of $\triangle ABC$. What is the scale factor?
What is the ratio of the perimeter of $\triangle DEF$ to the perimeter of $\triangle ABC$?
What is the ratio of the area of $\triangle DEF$ to the area of $\triangle ABC$?
In the figure below, what is the ratio of $x$ to $y$?
Claudia and Rodolfo were walking together on a sunny day. Claudia is 1.5 meters tall and casts a 2.1-meter shadow. How tall is her taller brother Rodolfo if he casts a shadow at the same time which is 0.42 meters longer?
Examine the following statement.
“If two triangles have one pair of angles congruent, the triangles are similar.”
If you disagree, give a counterexample showing that this statement is false.
Further Development
Jasmine has two triangles with equal angle measurements.
The sides of one triangle are 4, 6, and 8.
The sides of the
other are 9, 6, 12.
She says that the triangles are not
scaled copies because:
$$\frac{4}{9} = 0.444..., \textrm{ } \frac{6}{6}=1, \textrm{ and }\frac{8}{{12}} =
0.666...$$
Do you agree with Jasmine? Thoroughly explain your answer.
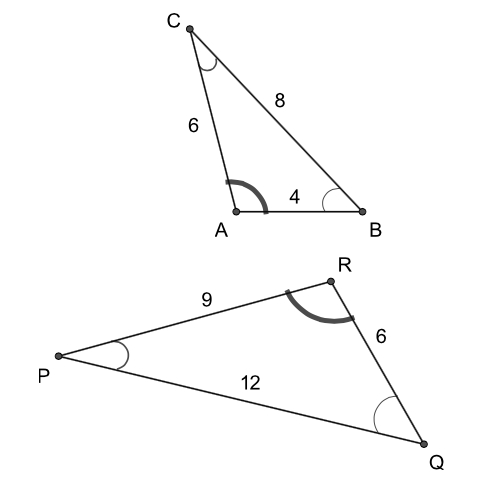
In two similar triangles, angles with the same measure are called corresponding angles, and sides opposite corresponding angles are called corresponding sides. As a matter of fact, in the previous problem, $\angle A$ and $\angle R$ are corresponding angles, and $\overline {BC}$ and $\overline {PQ}$ are corresponding sides. Given misunderstandings such as that of Jasmine’s in the previous problem, it is important to state explicitly what pair of angles have the same measurement when describing similar triangles. A natural way of doing this is by listing their corresponding angles in the same order. Thus, regarding the triangles in the previous exercise, we say that $\triangle ABC$ and $\triangle RQP$ are similar, and write $\triangle ABC \sim \triangle RQP$. The symbol $\sim $ is read “is similar to.”
$\triangle BUD \sim \triangle PAT$
$BU = 7$, $UD = 8$, $BD = 10$, and $PT = 12$.
Draw the figure and find $PA$.
Let $\triangle DEF \sim \triangle ABC$.
List all pairs of corresponding sides.
Let $k$ be the scale factor, that is,
the lengths of the sides of $\triangle DEF$ are $k$ times the lengths of the
corresponding sides of $\triangle ABC$. So, for example, $AB = k\cdot ED$.
Write two more equations
involving $k$, each one using a different pair of sides.
Solve each of the three equations for $k$.
In part c, you should have found three quantities that all equal $k$. Translate this into a statement about side lengths in similar triangles.
In the previous problem you may have concluded that if $\triangle DEF \sim \triangle ABC$, then
$$\dfrac{{DE}}{{AB}} = \dfrac{{EF}}{{BC}} = \dfrac{{FD}}{{CA}}$$
These equalities are also used to express that in two similar triangles corresponding sides are proportional. These equalities allow us to relate corresponding sides of similar triangles without explicitly mentioning the scale factor.
In the following figure, angles marked equally have the same angle measurements.
Take into account the convention stated in the paragraph above problem 17 to determine whether or not $\triangle ABC \sim \triangle DEF$. Explain your answer.
Describe the relationship between these two triangles using the $\sim$ notation.
Below, you have a list of equalities
between two ratios
relating to the triangles above. Determine which ones
are true and which ones are false, if any. Explain.
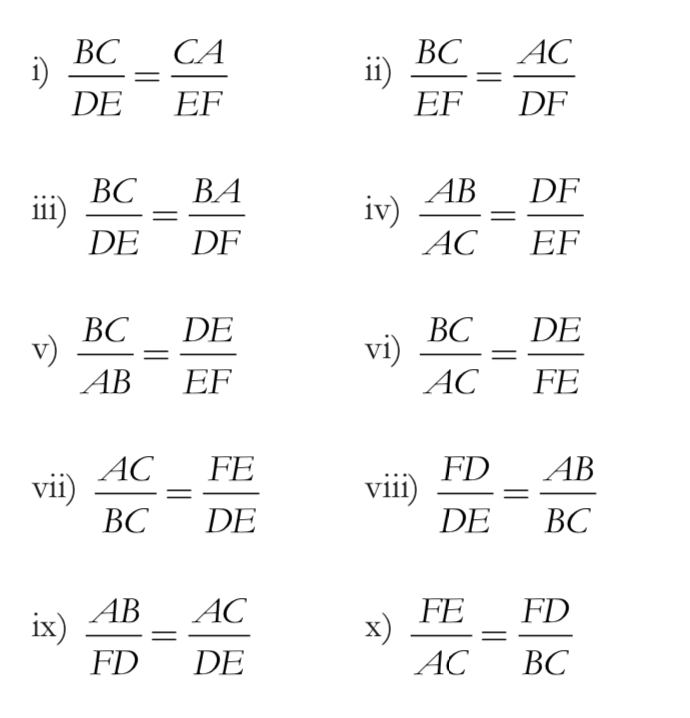
Practice
In the following figure, angles marked equally have the same angle measurements.

Is $\triangle PRQ \sim \triangle STU$? Explain your answer.
Describe the relationship between these two triangles using the $\sim$ notation.
Find $r$ and $u$.
In the following figure, angles marked equally have the same angle measurements, and $\overline {BD} $ and $\overline {AE} $ intersect at $C$.

Describe the relationship between these two triangles using the $\sim$ notation.
Find $x$ and $y$.
In this problem, you needed to use the fact that $\angle BCA$ was congruent to $\angle DCE$. Is this assumption justified?
In each of the following exercises, pieces of information about a pair of triangles are given. A figure is provided for exercise in Part a. In each case, find $x$.
Angles marked equally have the same
angle measurements.
$\triangle PQR \sim \triangle STU$, $PQ = 3$, $QR = x$, $ST = x$, and $TU = 7$.
$\triangle ABC \sim \triangle DEF$, $AB = x + 1$, $BC = 50$,
$DE = 2$, and
Felipe looks at a dot on a perpendicular wall 20 ft. away. If he looks .1 degrees to the right, he will be looking at a point on the wall about 3/8 of an inch to the right of the dot. Later Felipe (carefully) looks at the center of the Sun, which is 93 million miles away. If he looks at a sunspot that is .1 degrees to the right, how far away from the center of the Sun will he be looking? Would you estimate it was about:
16 miles to the right
1,600 miles to the right
16,000 miles to the right
160,000 miles to the right
16,000,000 miles to the right?
Now check your estimate by actually figuring out the answer.
Problems
Let $\triangle ABC \sim \triangle DEF$ and $k = \frac{DE}{AB}$ be the scale factor.
What is the ratio of the perimeter of $\triangle DEF$ to the perimeter of $\triangle ABC$? Justify your answer.
What is the ratio of the area of $\triangle DEF$ to the area of $\triangle ABC$? Justify your answer.
When studying similarity, it is important to determine when two angles in a figure have the same measurements. The following exercises will refresh or make clear some ideas regarding the angles formed when a line, called a transversal, intersects two parallel lines.
If line $r$ is parallel to line $s$, written $r \parallel s$, determine the angle measurements of the remaining angles shown in each of these figures.


In the following figure, $\overline {AB} \parallel {\overline {FD} }$, $\overline {BC} \parallel {\overline {DE} }$, and points $A$ and $C$ lie on $\overline {EF} $.

Are these two triangles similar? If so, say why and express their similarity using the $\sim $ notation.
In the following figure $\overline {BC} \parallel \overline {DE} $.
Determine all the angles in the triangles below.

Identify a pair of similar triangles in this figure. Using the $\sim $ notation, describe their relationship.
Given a triangle $PQR$, let point $S$ be on $\overline {PQ} $ and point $T$ on $\overline {PR} $ such that $ {\overline {ST} } \parallel \overline {QR} $. Determine whether there is any relationship between the triangles $PST$ and $PQR$. Explain your answer.
In the figure below $\overline {BC} \parallel \overline {DE}$. Find $x$ and $y$.
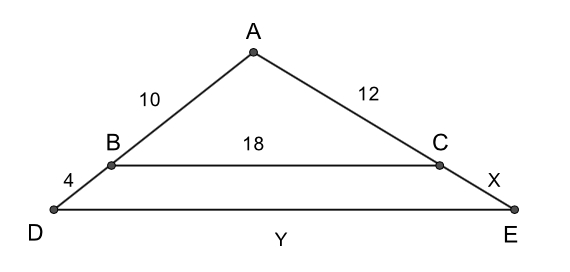
In a $\triangle ABC$, $BC = 9$ and point $D$ lies on $\overline {AB} $ 4
units from $A$ and 2 units from $B$. Furthermore, $E$ lies on
$\overline {AC} $ and
In a trapezoid, the lower base is 15, the upper base is 5, and each of the two legs is 6. How far must each of the legs be extended to form a triangle?
The height of the larger cone below is 9, and its slant height is 15. If the height of the smaller upper cone is 3, find its slant height $x$.

The shapes below are known to be scaled copies of each other. Calculate the missing side lengths for each of the two shapes.

In order to estimate its width, Amy, Bruce, and Carmen stood at the vertices of a right triangle ABC on one side of a river, with Bruce standing at the right angle. Their distances from one another are indicated in the figure below. If it is known that the distance between the tree and the rock shown on the other side is 20 meters, what is the width of the river?

An airplane P is flying at an elevation of 1720 m, directly above a straight highway. Two cars, C and A, are moving on the highway on opposite sides of the plane, and the angle of depression from airplane to car C is ${38^ \circ }$ and to car A is ${52^ \circ }$, as shown in the figure below (the dashed line is the imaginary horizontal line through P). If the second car is at a horizontal distance of $1343.8{\rm{ m}}$ to the right of the airplane, how far apart are the cars at this time?

Cindy, Jan, and Marsha have come up with an ingenious method for measuring the height of a tree. Marsha stands at a distance she measures to be 119.8 feet away from the tree. Jan walks 4/3 more feet away from the tree than Marsha. Cindy then finds a spot in which she can crouch down and see Jan’s head, Marsha’s head, and the top of the tree all in one continuous sightline. Cindy (when crouching) is 2.5 feet tall, Jan is 5 feet tall, and Marsha is 5.5 feet tall. Here is a diagram depicting the situation:
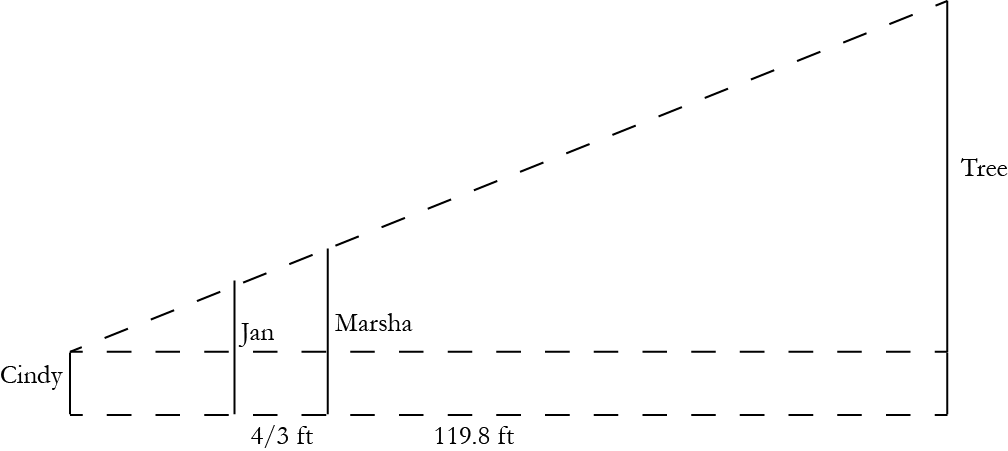
How far away from Jan did Cindy go in order to make this work?
How tall is the tree?
The two triangles below are similar but not congruent:
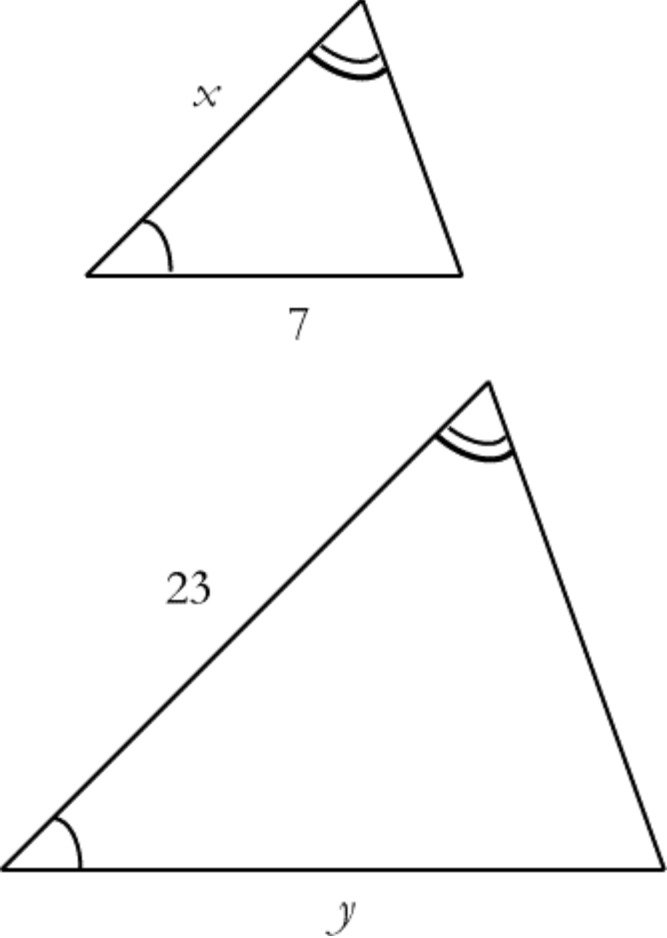
Can $x$ and $y$ both be integers, neither of them equal to 1? Why or why not?
In the figure below, right has been split into two smaller right triangles.
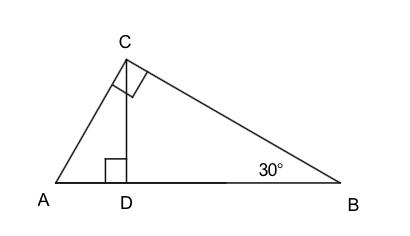
Find all the angles in the figure.
Name all pairs of similar triangles.
Regarding $\triangle IRT$ shown below, do the following.
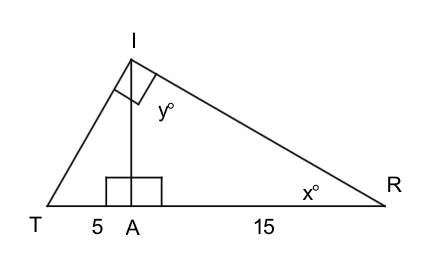
Mark in another angle whose measure is ${x^ \circ }$ and another whose measure is ${y^ \circ }$.
Name all pairs of similar triangles. Hint: Take things apart.
Calculate the length of $\overline {IA} $. Hint: Use similarity.
Calculate the length of $\overline {IR} $.
Calculate the length of $\overline {IT} $.
Check your answers by using Pythagoras’ theorem on $\triangle TRI$.
Andrew wanted to cover the upper part of his kite with yellow paper and the bottom part with blue paper (see figure). The leftmost and rightmost angles of the kite are right angles. Taking into account that the diagonals of a kite are perpendicular, how much paper of each color does he need?

$\triangle ABC$ is an equilateral triangle of side length equal to 1, that is, each side of this triangle is one unit long. $D$, $E$, and $F$ are the midpoints of $\overline {AB} $, $\overline {BC} $, and $\overline {CA} $ respectively. Determine the side lengths of $\triangle DEF$. Thoroughly explain your work.
Don’t use a calculator for this problem.
Add: $3\frac{5}{8} + 7\frac{7}{8}$
Factor: $4{x^2} - 16$
Factor: $14{x^2}{y^3} - 28{x^4}{y^2} + 7{x^2}y$
Reduce: $\frac{{2x + 12}}{{2x + 6}}$
Are lines with slopes $\frac{{42a}}{{ - 14b}}$ and $\frac{{7b}}{{21a}}$ parallel, perpendicular, or neither?
Consider an equilateral triangle with sides of length 1. This triangle is considered to be stage number 0 of the Sierpinski triangle. Then the central triangle obtained by joining the midpoints of each side is removed. This is considered to be stage number 1 of the Sierpinski triangle. Stage number 2 is obtained when from each of the three remaining triangles the central triangle is removed, as was done on the initial triangle when going from stage number 0 to stage number 1 (see figure below).
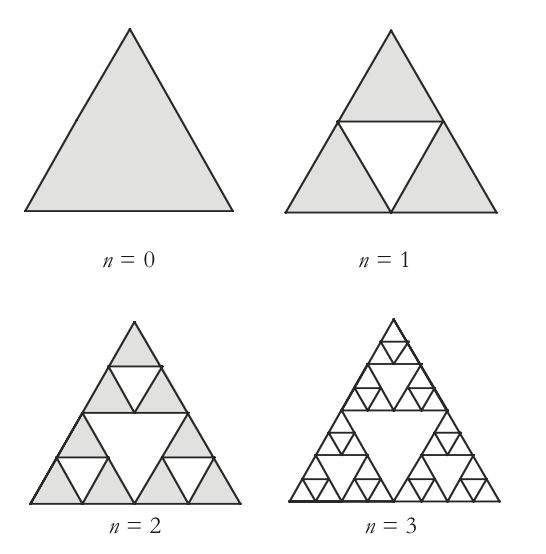
Appropriately shade the last triangle above to examine stage number 3. Then complete the table.
|
Stage number |
0 |
1 |
2 |
3 |
n |
|
Number of shaded triangles |
|||||
|
Total perimeter of shaded triangles |
|||||
|
Total area of shaded triangles |
Thinking of his will, Mr. Maury wants to leave a portion of his farm to each of his four children. This farm is a triangular piece of land whose dimensions are $1000$, $1200$, and $2000$ meters. However, Mr. Maury wants to be as fair as possible and leave pieces of equal size and shape to his children. Do you think that it is actually possible to split Mr. Maury’s farm into four pieces of equal size and shape? Thoroughly explain your answer.
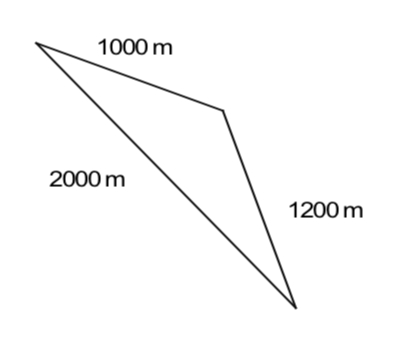
Is the result you found in Problem 44 true for any triangle? That is, is it always possible to divide a triangle into four triangles of equal size and shape? Explain.
Case SAS
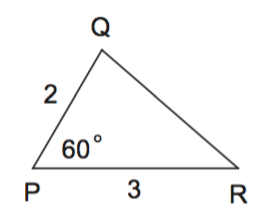

Regarding triangles $PQR$ and $STW$ above, we have the following:
$m\angle P = {60^ \circ }$, $PQ = 2$, $PR = 3$,
$m\angle S = {60^ \circ }$, $ST = 4$, and $SW = 6$.
Are these two triangles similar? How could you justify your answer?
For each statement below, draw a picture illustrating it. Then decide whether or not this statement is true. For each “Case” with which you disagree, give a counterexample showing that it is false.
AA Case
If two angles of one triangle are congruent to two angles of
another triangle, then the two triangles are similar.
SSS Case
If the three sides of one triangle are proportional to the
three sides of another triangle, then the two triangles are
similar.
SAS Case
If the following conditions are met:
i) Two sides of one triangle are proportional to two sides of
another triangle. That is, the lengths of two sides of one
triangle are a constant times the lengths of two sides of the
other triangle.
ii) The included angles are
congruent. That is, the angle formed in one of the triangles by
the two sides that are proportional to two sides of the other
triangle is congruent to the corresponding angle in the other
triangle.
Then the two triangles are
similar.
SSA Case
If two sides of one triangle are proportional to two sides of
another triangle and the angle opposite one of those sides of
the first triangle is congruent to the corresponding angle
opposite one of those sides of the second triangle, then the
two triangles are similar.
A certain crop of black-eyed peas has been genetically altered such that each pea is flat and perfectly circular, and its “eye” runs in a straight line through the center of the pea. The $PeaEye$ function takes any pea and divides its circumference by the length of its eye. If pea #1 is twice the size (total area) of pea #2, then which is bigger: $PeaEye\left( {pea\# 1} \right)$ or $PeaEye\left( {pea\# 2} \right)$?
Exploring in Depth
In a triangle, a segment drawn from a vertex of a triangle perpendicular to its opposite side, or to the extension of its opposite side, is called an altitude to this side of the triangle.

If in a right triangle the altitude to the hypotenuse is drawn, the hypotenuse is divided into two segments. The lengths of these segments and the length of the altitude to the hypotenuse are related. This relationship has already been revealed in Problem 39. In the following problems, we will try to make this relationship more explicit.
In the right $\triangle ABC$ below, draw the altitude $\overline {CD} $ to the hypotenuse. Then:
Mark in all the angles that turn out to be congruent.
Name all pairs of similar triangles. Justify your answer.

Very likely, you have been using the Pythagorean Theorem for quite some time now. However, have you ever created a formal proof of this theorem? You might not have known enough until now.
Regarding a right triangle as the one below, answer the following questions.

Write an equation relating, $h$, the length of the altitude to the hypotenuse, with $m$ and $n$, the two lengths into which this altitude divides the hypontenuse. Hint: Consider triangles $\triangle ADC$ and $\triangle CBD$.
Write an equation relating the legs, the hypotenuse, and the length of the altitude to the hypotenuse. In other words, write an equation involving a, b, c, and h in the above triangle. Hint: Consider triangles $\triangle ABC$ and $\triangle ACD$
$\overline {AD} $ is called the projection of leg $\overline {AC} $ onto the hypotenuse $\overline {AB} $. Also, $\overline {DB} $ is the projection of leg $\overline {CB} $ onto the hypotenuse $\overline {AB} $. How is each leg related to the hypotenuse and its projection onto the hypotenuse? In other words, write an equation relating $a$, $c$, and $n$ in the triangle shown above. Then write an equation, relating $b$, $c$, and $m$. Hint: Consider $\triangle ABC$ and $\triangle CBD$, and $\triangle ABC$ and $\triangle ACD$.
Use Part c above to prove the Pythagorean Theorem. That is, prove that ${a^2} + {b^2} = {c^2}$.
In the figure below, $\triangle ABC$ is a right triangle and $\overline {CD} $ is the altitude to the hypotenuse. As shown in the figure, the lengths of the projections of the legs $b$ and $a$ over the hypotenuse are, respectively, $m = 3$ and $n = 9$. Find $h$.
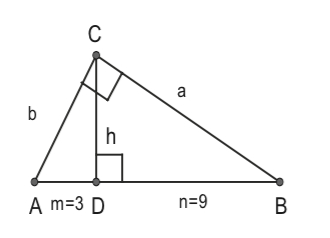
In the figure below, $\triangle ABC$ is a right triangle and $\overline {CD} $ is the altitude to the hypotenuse. As shown in the figure, the lengths of the projections of the legs $b$ and $a$ onto the hypotenuse are, respectively, $m = 4$ and $n$. As usual, $c$ is the length of the hypotenuse $\overline {AB} $.

Find AB.
Find $h$.
Let us recall Andrew’s kite problem (#40).
Can you use the ideas developed in the problems of this section to find out how much paper of each color Andrew needs to cover his kite?
