Introduction
The escalator at the Wheaton metro station in Silver Spring, Maryland, is the longest escalator in the Western Hemisphere. If you ride it you will travel a diagonal distance of 508 feet, which will take two minutes and forty-five seconds. You’re about to build a bigger one – your goal is to make an escalator with a diagonal distance of 520 feet. Before you can start, though, you need to do some planning. You need to figure out how much space along the ground your escalator will take so that you can prepare the foundation. Standard escalator construction rules require that:
- the steps each be 1.2 feet long
. - The measure of the angle between the ground and the diagonal path of the escalator must be no more than 30°
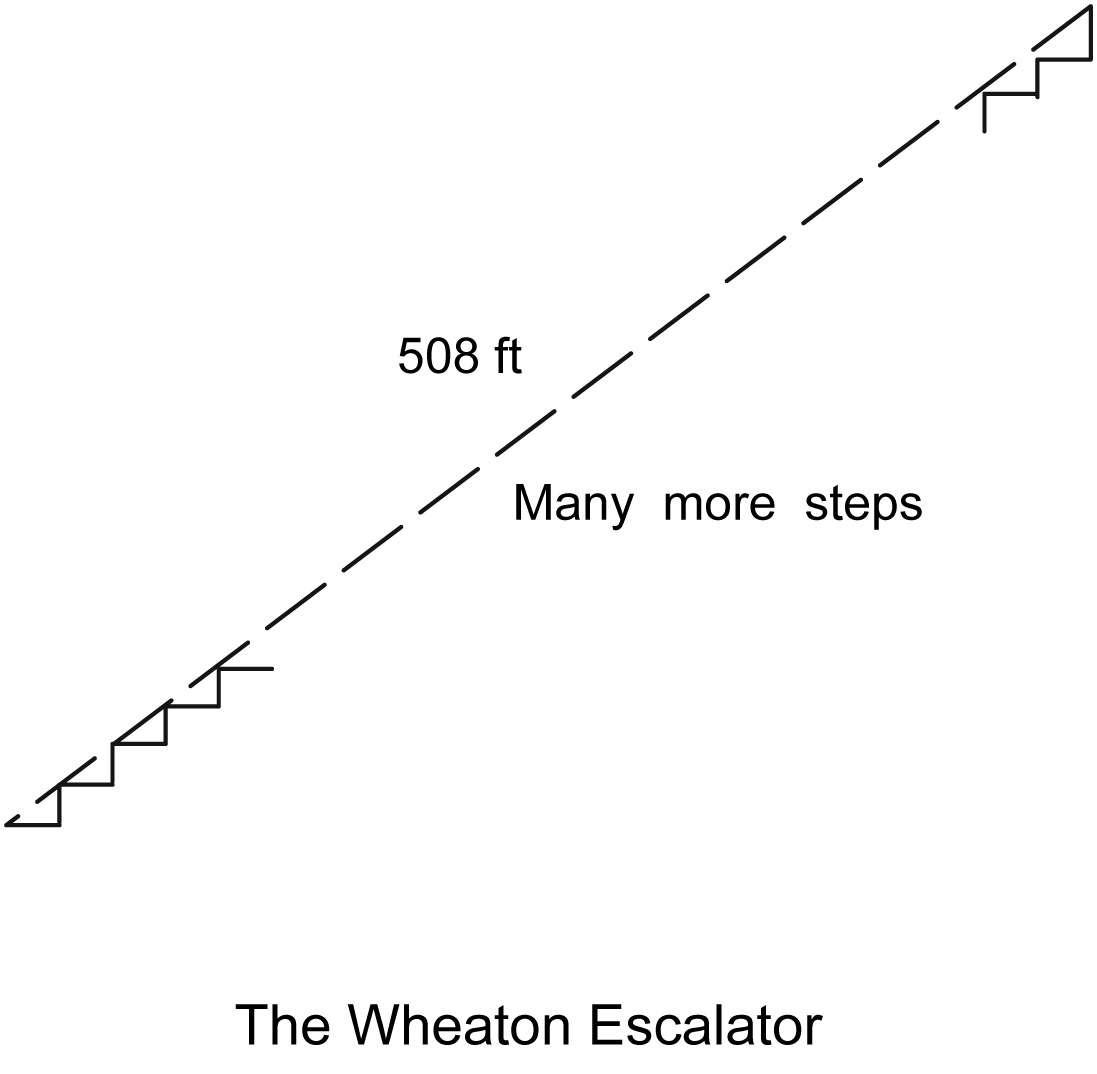
You start to build your escalator and measure a diagonal distance of 1.3856 feet per step. What is the horizontal distance, along the ground, you’ll need to clear in order to build your escalator with a diagonal distance of 520 feet?

Development
Your solution to the escalator problem probably involved ratios or scale factors in some way. Here’s one way of thinking about the problem:
If you haven’t already, explain how you know that $\frac{1.2}{1.3856} = \frac{\textrm{the required horizontal distance}}{520}$.
Use a similar method to find the height of the Wheaton escalator.
Imagine a large right triangle $ABC$ with the right angle at $A$ and angle $C = {30^ \circ }$. Based on your work in problems 1-3:
What would you expect the ratio of $AC$ to $BC$ to be? Why?
How about the ratio of $AB$ to $BC$?
Go ahead and check your thinking by using a protractor and ruler to accurately draw such a triangle, and measure the sides. Convince yourself that these ratios are the same no matter how large or small the right triangle is, provided the measure of angle $C$ remains 30°.
As problem 4 emphasizes, certain ratios will always stay constant in a right triangle with an angle measuring 30°. In the escalator example, the ratio of the vertical distance to the diagonal distance is called the sine of 30°. The ratio of the horizontal distance to the diagonal distance is called the cosine of 30°.
A third ratio is called the tangent ratio. In the escalator example, this is the ratio of the vertical distance to the horizontal distance.
If you asked your calculator to tell you the sine of 30° what do you suppose it would give you? How about the cosine of 30°? Tangent of 30°?
If you think of the escalator as a triangle with a 30° angle and a 90° angle, you can label the sides as follows:

There are two sides that form the 30° angle. One is of course the hypotenuse; the other is called the side adjacent to the 30° angle. The vertical side of the triangle is called the side opposite to the 30° angle, since it is all the way across the triangle from the angle.
For each of the following, use a protractor to draw a RIGHT triangle with the angle given. Then use a ruler to measure the lengths and calculate the sine, cosine, and tangent of each angle.
25°
63°
42°
For each part in the previous problem, use the SIN, COS, and TAN buttons on your calculator to see how close your estimates were.
Here’s the picture in general. We’re using $\theta$ (“theta”) to stand for any angle, just like we can use $x$ to stand for any number.
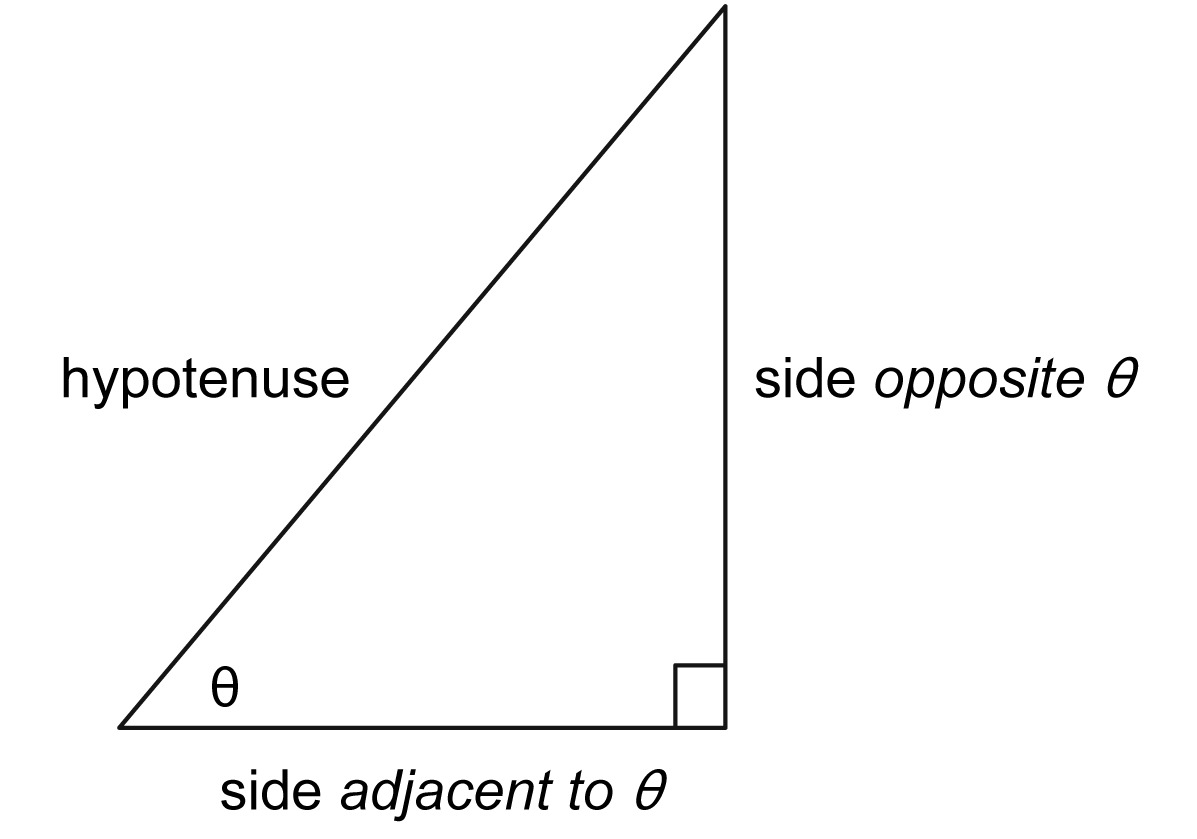
If $\theta$ is an angle in a right triangle, but not the right angle, then here’s how we define the three trigonometric ratios:
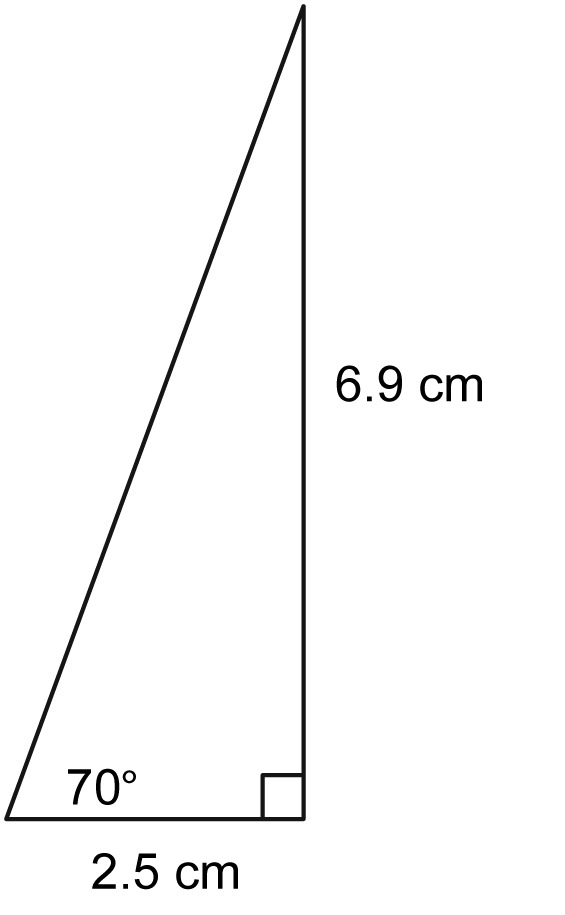
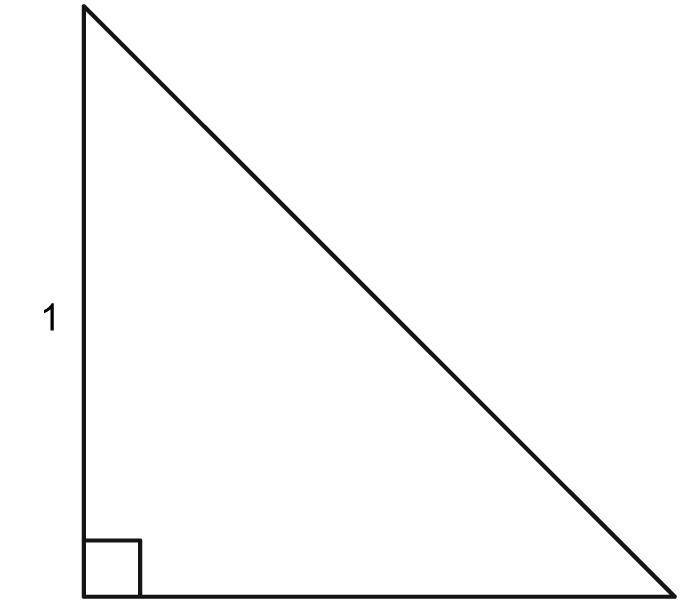
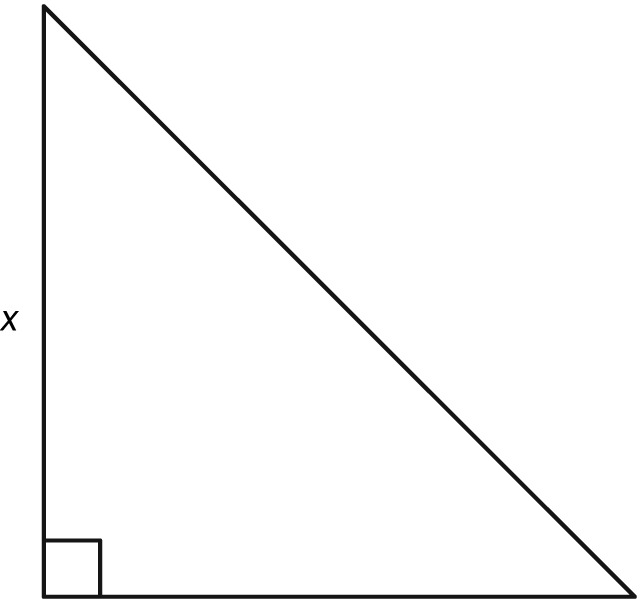
$$\sin(\theta)= \frac{\textrm{opposite}}{\textrm{hypotenuse}}$$ $$\cos(\theta)= \frac{\textrm{adjacent}}{\textrm{hypotenuse}}$$ $$\tan(\theta)= \frac{\textrm{opposite}}{\textrm{adjacent}}$$Using the two triangles below, find the sine, cosine, and tangent of a 70° angle, a 20° angle, a 35° angle, and a 55° angle.

Did you notice any repeated answers in your calculations above?
Make a conjecture based on your findings.
Try out your conjecture on a triangle that you create.
Can you explain why this is going on?
In the similar triangles lesson, and also in the escalator problem, you were able to find missing lengths in certain triangles because you had a second, similar triangle that allowed you to find the scale factor. One reason that sine, cosine, and tangent ratios are so important is that they help you find lengths in triangles even when you don’t have a second triangle to help you get the scale factor.
Here is a problem that allows you to “solve a triangle” using only trigonometry.
Use this triangle to write an expression for the tangent of 35 degrees. Your expression will, of course, contain the letter $x$.

Using the equation “$\tan {35^ \circ } = ...$”, find $x$. (You should know the value of $\tan 35^\circ $ from a previous problem)
Find the length of the hypotenuse of the triangle.
In the previous problem, you were lucky that you already knew the tangent of 35°. You are not always so lucky. However, your calculator can help you out.
Press the MODE button on your calculator and make sure “degree” is selected. Then type “tan(35)”. The number on your screen should look familiar.
Find both of the missing sides in the following triangle:

Often, trigonometry is used to find lengths of triangles in the “real world” that are too difficult to measure directly.
You’d like to know how tall a flagpole is, but you can’t reach the top to measure it. So instead you use your tape measure to measure 50 ft along the ground. Standing 50 ft away from the flagpole, you can see the top of the flagpole by looking up at a 22° angle. How tall is the flagpole?
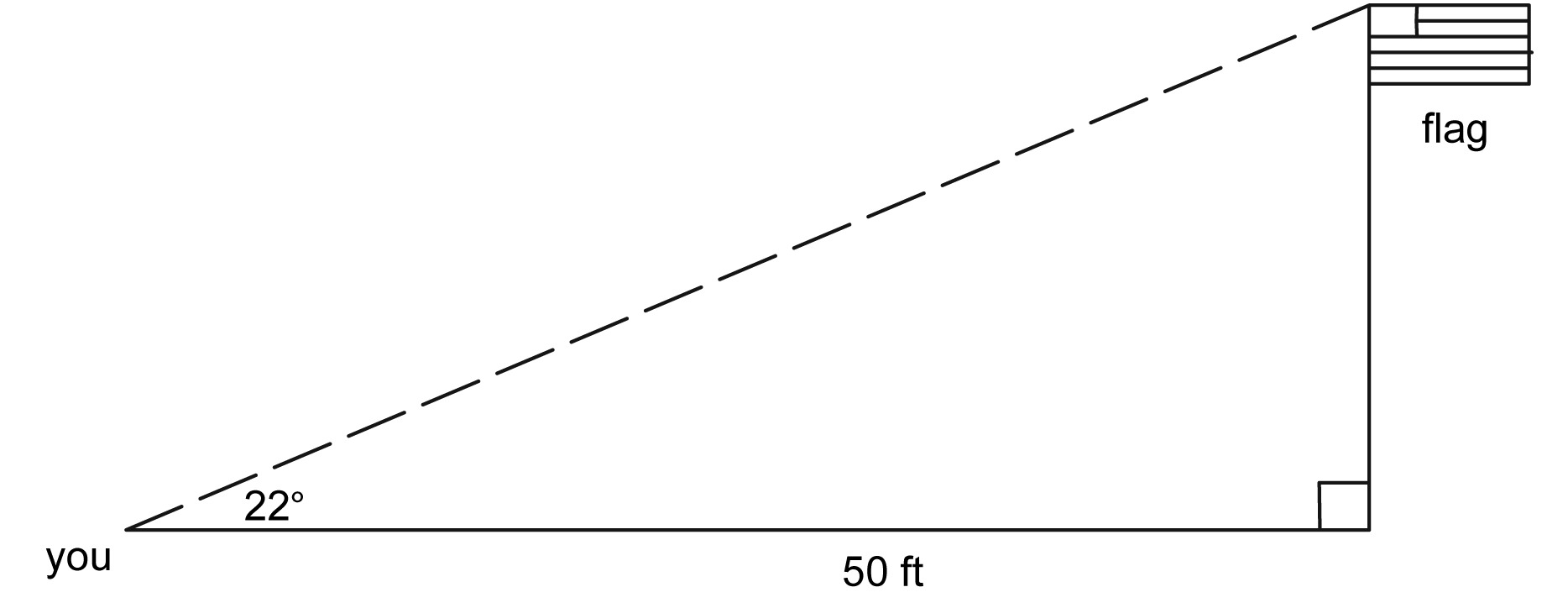
In the previous problem, you might have ignored your height. Say your eyes are at a level of 5 feet 6 inches above the ground. Taking this into account, figure out how tall the flagpole really is.
Practice
Find the length $x$ in each triangle.



Stephen can see the head of the Loch Ness Monster if he looks up at an angle of 35°. He’s standing on the level floor of a shallow lake, and he’s six feet tall. If it is 20 yards along the ground from where he’s standing to where the Loch Ness Monster is standing, how tall is “Nessie”?
Think about the location of Stephen's eyes. Is your answer to the previous question actually a little bit too big, or a little bit too small?
A 20-ft ladder is placed against a wall at an angle of 72 degrees with the ground.
How far from the base of the wall is the ladder?
How high does the ladder reach on the wall?
Problems
Your fifth-story apartment window looks out over a courtyard 50 feet long. To see your friend in the eighth-story window across the courtyard, you need to tilt your head up at a 31° angle. How far apart are the floors positioned in your apartment building? (Assume they’re spaced evenly).
Say that, for some angle $\theta$, $\sin \theta = \frac{5}{8}$. Mark’s triangle has a 90° angle and an angle of $\theta$. The side opposite $\theta$ is 45 cm long. How long is the hypotenuse of Mark’s triangle?
The sine of 25 degrees is about .4226. What angle has a cosine of about .4226?
John looks at a building whose base is 100 ft. away from where he is standing. He sees a friend leaning out of a window at an angle of elevation of 30 degrees. His friend yells to him that the people in the building are part of a “flash mob” (see http://en.wikipedia.org/wiki/Flash_mob), and that a mutual friend will be appearing at a window that is twice as high up. So John looks at the window at an angle of elevation of 60 degrees, but their mutual friend never appears. Why?
In problems 23-27, geometric tinkering will prove very helpful.
Find $x$.
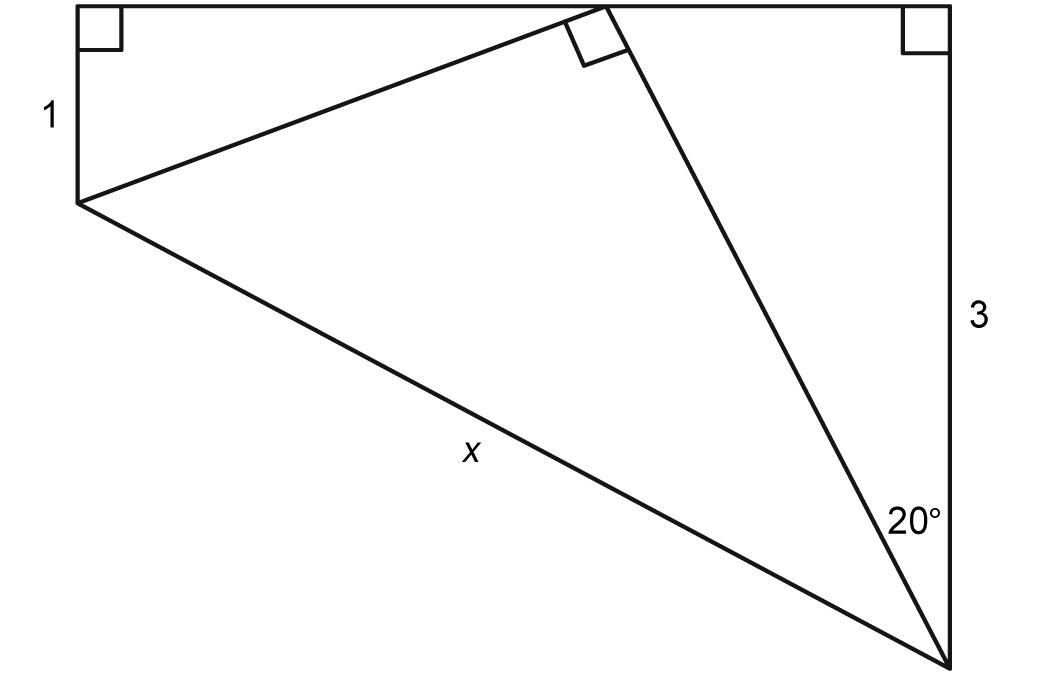
Find $x$.
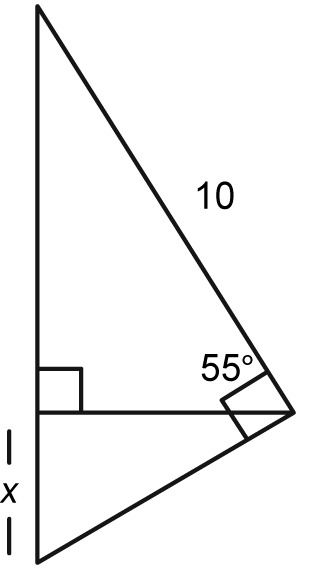
Find $x$.

Your calculator gives you approximate answers when you ask it to tell you the sine, cosine, or tangent of an angle. (See http://www.mathsisfun.com/irrational-numbers.html for more information and a juicy, though probably apocryphal, tidbit.) Sometimes you would rather know the answer exactly. Some geometry can help you do this.
Below are two triangles. The first one is an equilateral triangle. The second is an isosceles right triangle.

Find all the sides and angles in the figures on the previous page, including the height of the equilateral triangle. Do not use a calculator, and do not convert your answers to decimals.
Here are two more triangles. Again, the first is equilateral and the second is an isosceles right triangle.

Now find all the sides and angles. You’ll have to give some of your answers in terms of $x$.
Your answer to the previous exercise turns out to be tremendously useful. For instance, let’s say that you have a triangle that you know to have angles of 30, 60, and 90 degrees. We’ll call this a 30-60-90 triangle. Normally, you’d need to know two sides of a right triangle in order to figure out the third side of a triangle. But the result in the previous exercise can help you find both missing sides.
For example, say you have a 30-60-90 triangle with its shortest side of length 3. Find the lengths of the other two sides.
Suppose you have a 30-60-90 triangle and the hypotenuse has length 5. What are the lengths of the other two sides?
Find the lengths of the legs in a 45-45-90 triangle if the hypotenuse has length $7\sqrt 2 $.
If you haven’t already, make a good sketch in your notebook of a 30-60-90 triangle with shortest side $x$, and label its other sides in terms of $x$. Then do the same thing for a 45-45-90 triangle.
Copy the following chart into your notebook and use the diagrams you drew in problem 31 to help find exact values for the sine, cosine, and tangent of the following angles.
|
$\theta$ |
Sine of $\theta$ |
Cosine of $\theta$ |
Tangent of $\theta$ |
|
30° |
|||
|
45° |
|||
|
60° |
Sally spies Bigfoot, who is a bit too close for comfort. With her trusty protractor in hand, she notices that, if she looks up at a 60-degree angle, she can just see the bald spot on the top of his head. When Bigfoot sees her protractor, he shies and runs away. Sally then measures along the ground to the spot where he was standing, and finds that he was 10 meters away. Five-foot-tall Sally can calculate exactly how tall Bigfoot is. Can you?
Now that Sally knows how tall Bigfoot is, she decides to spy on him from a distance. If she can now see the top of his head by looking up at a 30° angle, exactly how far away is she from Bigfoot?
Kenya computes the sine of 45 degrees from her isosceles right triangle and gets $\frac{1}{{\sqrt 2 }}$, while Victoria computes the sine of 45 degrees from her isosceles right triangle and gets instead $\frac{{\sqrt 2 }}{2}$. Are these answers actually the same answer, or not? Explain.
Are there other right triangles besides 30°-60°-90° triangles for which one of the sides is half the length of the hypotenuse?
Recall that an altitude of a triangle is a line segment drawn from the vertex of a triangle at a right angle to the line containing the opposite side.
The three altitudes of an equilateral triangle all have length 12 cm. How long are its sides?
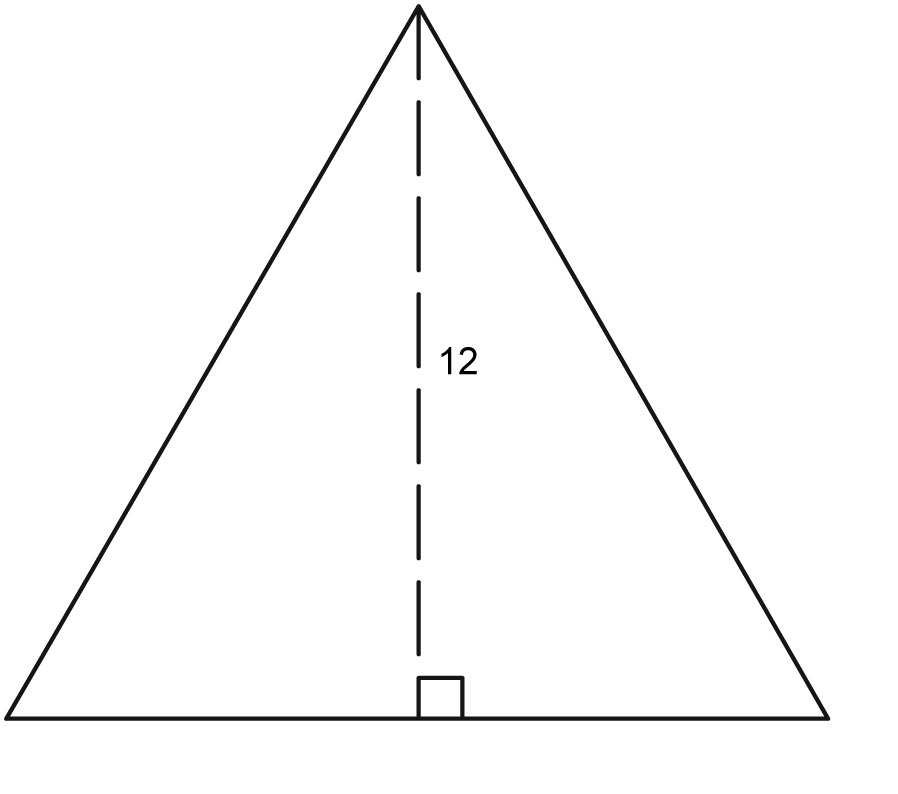
An isosceles triangle has two $65^\circ $ angles. The altitudes drawn from those angles are 12 cm. What are the lengths of the three sides of the triangle? Answer to the nearest tenth of a millimeter.
Suppose you have a rectangle with dimensions a and b. The Oblongness function is defined by: ${\rm{Oblongness}}(a,b) = \frac{{{\rm{max}}(a,{\rm{ }}b)}}{{{\rm{min}}(a,b)}}$.
Draw rectangles with the following oblongnesses: 3, 10, 1.618.
For which pairs of values of a and b is ${\rm{Oblongness}}(a,b)$ as small as possible?
Wouldn’t it be easier to just define ${\rm{Oblongness}}(a,b)$ simply as $\frac{a}{b}$? Why is the given definition better?
Cody has a rectangle, in which he has drawn one diagonal. He finds that the angle between the diagonal and the long side of the rectangle is 12 degrees. What is the oblongness of Cody’s rectangle?
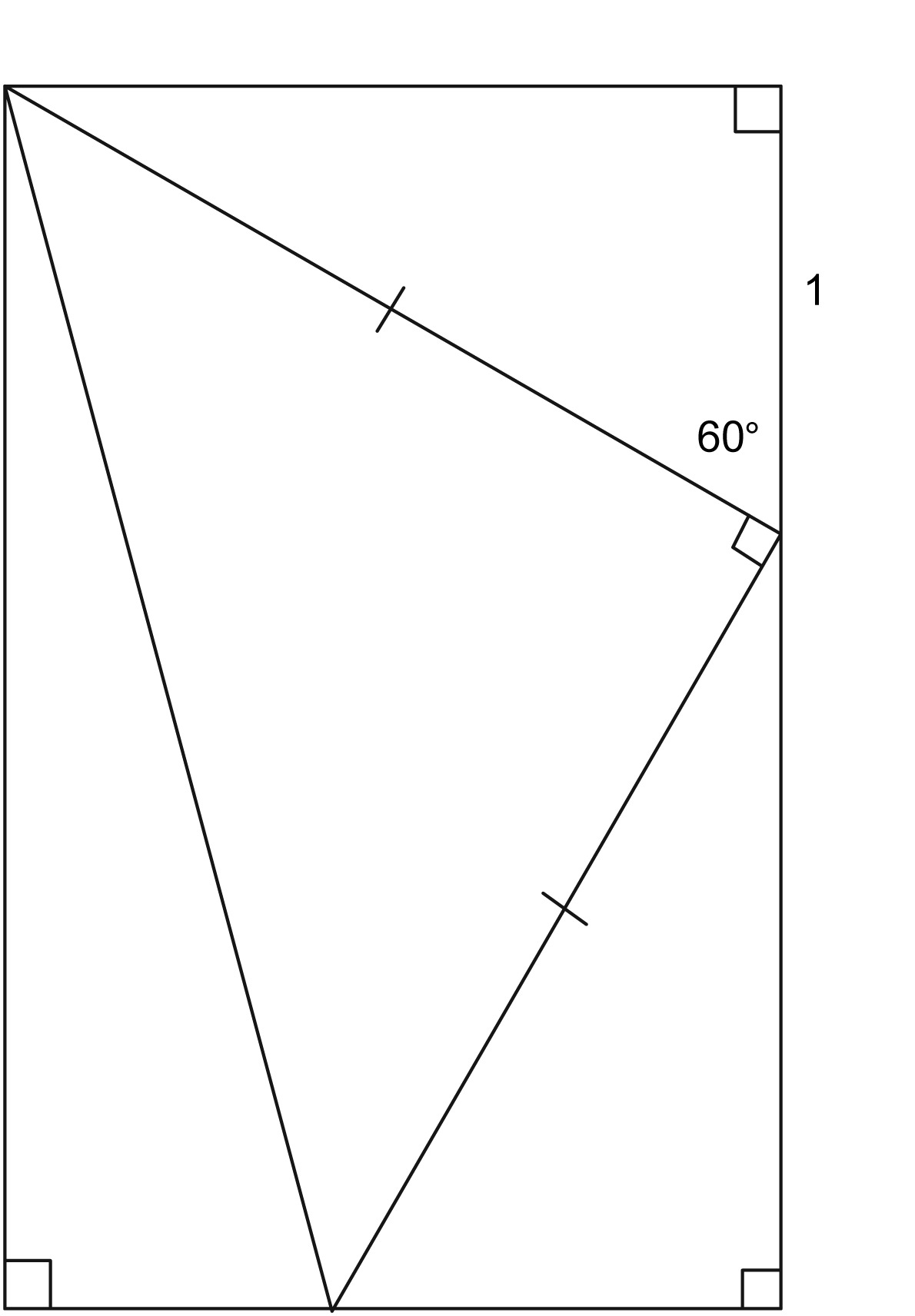
This diagram shows a rectangle that has been formed by bordering an isosceles right triangle with three other right triangles, one of which has a 60-degree angle as shown.
Given that the length marked is 1 unit long, find as many lengths and angles in the picture as you can. (Give answers in exact form.)
Use this diagram to find the exact value of the sine of a 75-degree angle.
Susan and Emily are both standing on an east-west sidewalk, looking at the top of a 20-foot building. Susan is standing due south of the building, and has to look up at an angle of 50° to see it. Emily, who is standing to Susan’s right, has to look up at an angle of 35° to see the building. How far apart are Susan and Emily?
Don’t use a calculator for this problem.
Simplify: $- (7x)(x - 5)$
Simplify: $3(x-1) - 2(x-4)$
Solve the inequality $\left| {x - 5} \right| > 7$.
Factor: ${x^2} - 9x + 20$
Solve for $x$: $\frac{2}{x} - 5 = 4$
In the diagram below, find $x$ and $y$.

The following questions are related to a famous puzzle called “Buffon’s needle,” which you may want to look up if you are interested.
You’re throwing a tiddlywink with a 4 cm radius onto a floor with square tiles measuring 12 cm on a side. What’s the probability that the tiddlywink will make it onto the floor without landing on a crack?
Now you’re playing a different version of the game, where you throw a needle between evenly spaced stripes on the floor. Your needle is 2 inches long, and the stripes are also 2 inches apart. Assuming that the needle will land at an angle of 72 degrees to the stripes, what’s the probability that it will land without overlapping any of the stripes?
Here are some questions about an “extreme value” of the sine.
Ask your calculator to tell you the sine of an 80° angle. Then ask for the sine of an 89° angle. Does this suggest a value for the sine of a 90° angle? Have your calculator confirm your guess.
Using a protractor, draw a right triangle with an 80° angle. Then measure the hypotenuse and the side opposite the 80° angle. How do they compare? How do you think those two sides would compare in a right triangle with an 89° angle?
Have a conversation with a classmate (or friend, guardian, spiritual advisor) about how someone might have decided what the sine of a 90° angle should be. Remember that our definition of sine as $\frac{{{\rm{opposite}}}}{{{\rm{hypotenuse}}}}$ in a right triangle won’t quite work.
Exploring in Depth
(Problems 46-49 copyright Phillips Exeter Academy.)A rhombus has four 6-inch sides and two 120° angles. Two altitudes are drawn in from one of the 120° angles. Find the area of each of the three pieces of the rhombus.

A right triangle has a 24 cm perimeter, and its hypotenuse is twice as long as its shorter leg. Find the lengths of all three sides of this triangle.
A triangle has a 60-degree angle and a 45-degree angle, and the side opposite the 45-degree angle is 240 mm long. To the nearest mm, how long is the side opposite the 60-degree angle?
A line of positive slope is drawn so that it makes a 60 degree angle with the x-axis. What is the slope of this line?

Play the “Buffon’s needle” game: take a needle and draw parallel lines on a sheet of paper, spaced the needle’s length apart. Toss the needle so that it lands on the paper, and record whether the needle crosses a line or not. Pool your data with others who have played the game, and use the data to compute the probability that a needle thrown on the paper will cross a line. Once you have the probability, try dividing by two and then taking the reciprocal of your answer. This process should result in something close to a number with which you’re familiar.
Pick an angle, any angle. Use your calculator to find its sine and cosine. Now square each of these numbers and add them together. Try it again with another angle. Notice anything? Write down your conjecture in as concise a form as you can.
Let’s try to prove your conjecture in Problem 51. Draw a right triangle $ABC$, with the right angle at $C$, and use $a$, $b$ and $c$ to represent the lengths of the sides opposite angles $A$, $B$, and $C$ respectively. Write ratios for $\sin A$ and $\cos A$, and with the help of the Pythagorean Theorem, prove your conjecture.