Introduction
So far, the trigonometry that you’ve learned applies specifically to right triangles. Even with shapes you see around you that don’t look like right triangles, with a little creativity you can still analyze these shapes using right triangles.
An “octastar” is a perfectly regular eight-pointed star.
Find two different ways to split up the octastar into right triangles.

Here’s a regular pentagon with each side measuring 2 inches.

Find the measure of each angle of the pentagon by first drawing a circle around the pentagon. (You might want to use the center of the circle.)
Let’s split this pentagon into six right triangles. (You can assume that the lines that look vertical and horizontal are vertical and horizontal.) Fill in all the angles that you can figure out in the new diagram.

Now that you have all the angles, what more do you need to find in order to calculate the area of the pentagon? (Saying what you need to find is enough… you don’t need to actually calculate the area.)
Development
In the diagrams so far, every drawing has been split up by turning it into a collection of right triangles pieced together – in other words, you add up the triangles to get the picture you want. Here’s a slightly different way to use that strategy. Suppose you’re investigating the following triangle:

You could split it into two right triangles by adding the following line:

But suppose for some reason you didn’t want to split up the long side of the triangle. Instead, you might notice that if you add a small right triangle on to your diagram, you get a big right triangle:
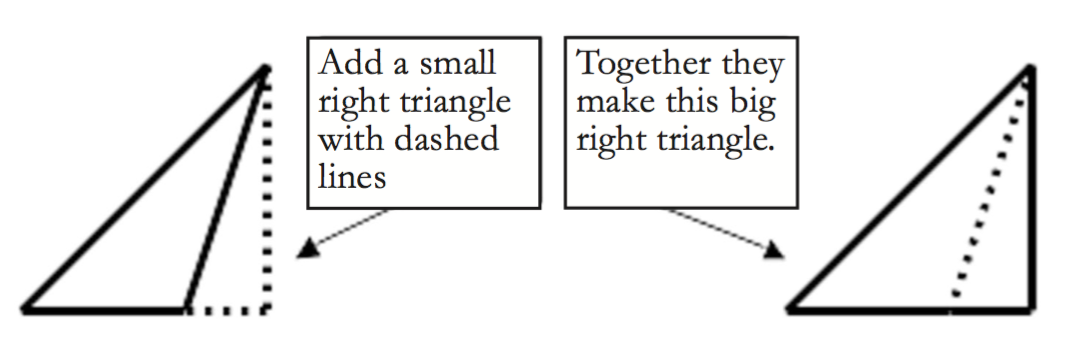
One strategy to think about when you visualize a problem is that you can alter the diagram to see it in a new way. Finding a new way to see a picture, or figuring out an interesting way to split a diagram into pieces, can give you insight into the problem.
In the diagram below a circle is fitted exactly into a square. The center of the circle is O and the length of diameter AB is 3.5 cm. What is the area of the square?

Find the area of this shape:

Split each of these three identical triangles into two right triangles, each in a different way.
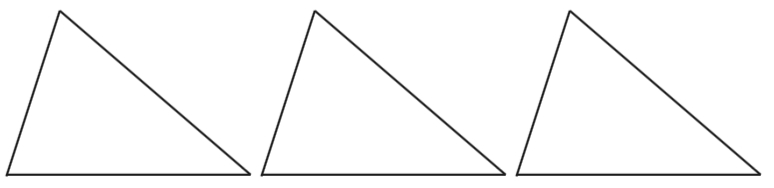
The line segments you used to split the triangles in problem 5 are called altitudes.
Why do you think they are so named? Write a clear definition of an altitude.
Draw altitudes for the three identical triangles below, each in a different way.

For the rest of this lesson, your numerical answers should either be exact or have 2-decimal place accuracy, unless you are asked to estimate an answer.
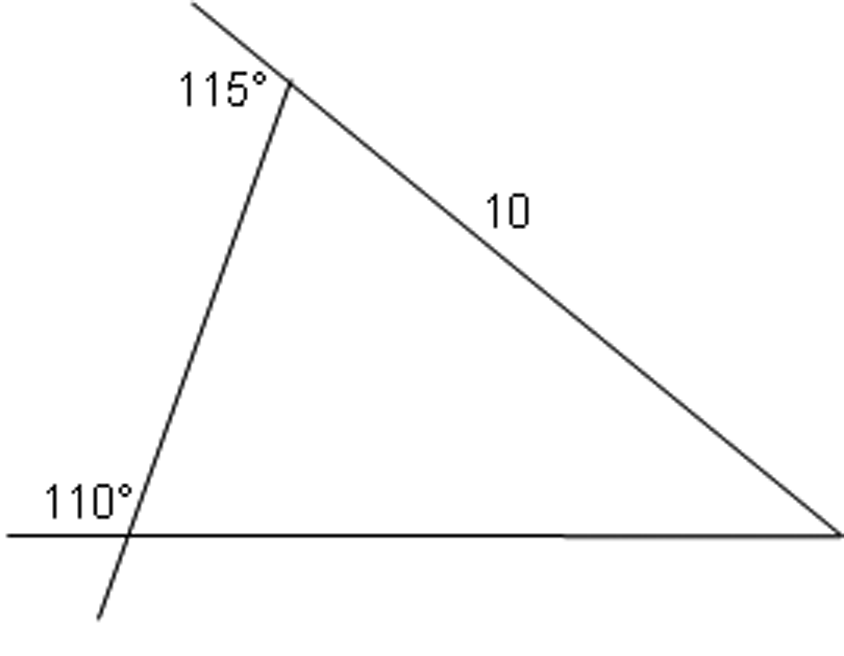
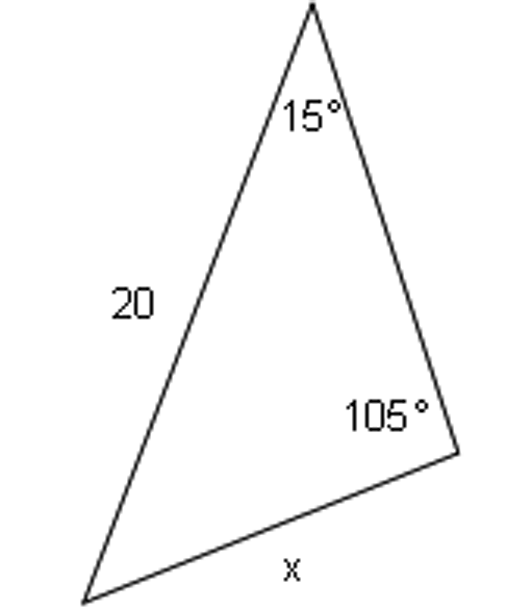
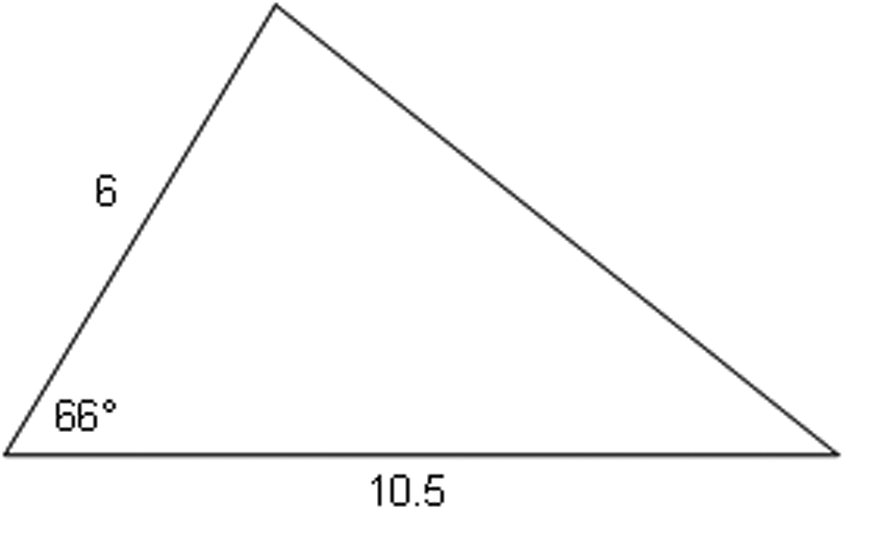
Use trigonometry to find the lengths of all the sides of the bold triangle.

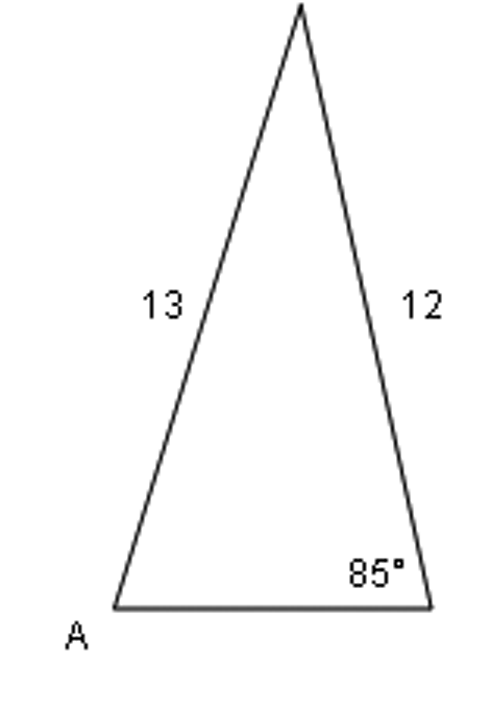
Use trigonometry to find the lengths of all the sides of the triangle.
Use trigonometry to find the lengths of all the sides of the triangle.

Inverse Trigonometry
So far, given the right information, you have been able to find the length of sides of a triangle, and might well wonder if there might be a way to find the angles when the appropriate information has been given. For example, could you find the angle at the top of the right triangle below? You could take a guess, check your result, and refine your guess.

Make a guess. Think about how you could test your guess for accuracy, given what you know about sines (or cosines). Test it and adjust your guess until you get the correct answer to the nearest degree.
There are ways to figure out the trigonometry of every angle exactly, but when you type “sin 67”, for example, into your calculator, it is basically looking the answer up on a table: sin 67° is about .9205.
Now suppose you know that an angle has a sine of .9205, but you don’t remember the degree measure of the angle. You can try to figure out the angle, as you did in problem 10 above, using reasoning. Or, you can use your calculator to look at the sine table, backwards – this is like asking “The sine of what angle would give me .9205?”
To do this, first make sure your calculator is set in degree
mode. Then, type
Practice

In this right triangle, what is the sine of angle A? Use your calculator (inverse trig) to find A.
What is the tangent of angle A? Use inverse trig with this number to find angle A. (Your answer should be the same as that of part a!)
Find the measure of angle $A$ in the picture below.
Find $x$ in each problem.


For the picture below, decide if each statement is true or false. If you think a statement is false, say why.
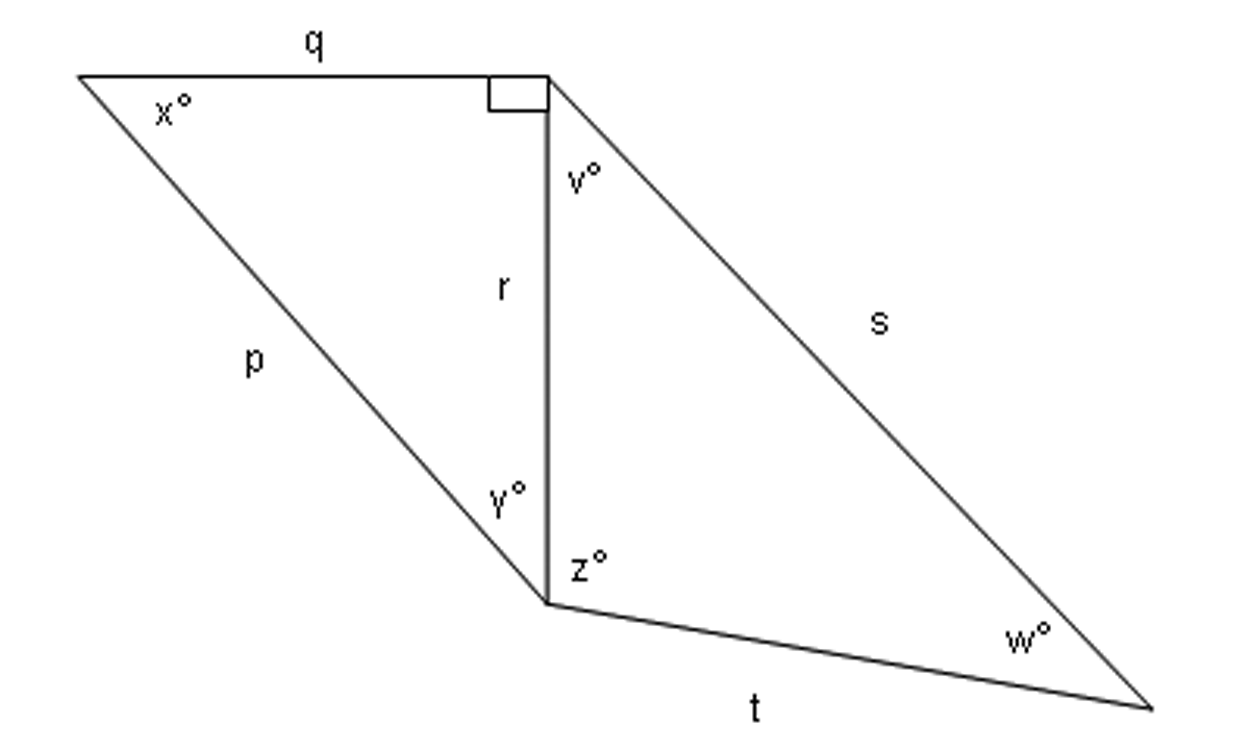
${p^2} + {q^2} = {r^2}$
$\sin {w^{\rm{o}}} = \frac{r}{s}$
$\sin {y^{\rm{o}}} = \frac{r}{p}$
$\tan {x^{\rm{o}}} = \frac{r}{p}$
$r^2 + t^2 = s^2$
Solve for $x$ in each equation.
$\sin x = .57$
$1.3 = \tan x$
$6\cos x = 5$
$\frac{\sin{x}}{6}=.12$
$16 = \frac{{10}}{{\tan x}}$
Problems
Angles of Descent and Elevation
In real-world problems, angles are often measured relative to the ground, or to the horizontal.
In this diagram, the plane is taking off at an angle of elevation of 15°.

In this diagram, the plane is landing with an angle of descent of 25°. Another name for this angle is the angle of depression.
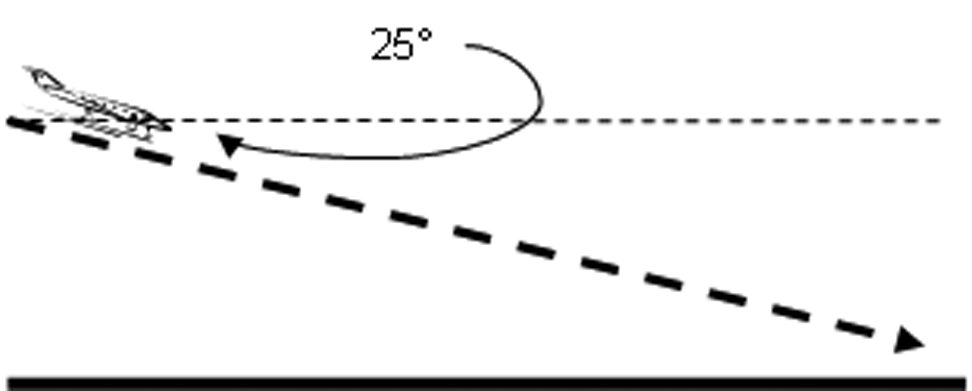
The descending plane in the picture above is 100m above the ground. The angle of descent is 25° as shown. How far in the air does the plane fly from where it starts in the picture to where it lands?
Two trees are leaning on each other. The tree on the left is 11.5m long, at an angle of elevation of 26°. The tree on the right has an angle of elevation of 11°. Find the length of the second tree.

A bird is sitting on top of a pole, looking at a bug on the ground. The bug is 8 ft from the base of the pole, and the bird’s line of sight down to the bug has an angle of depression of 55°. Draw a diagram to represent the situation, and determine the height of the pole.
A plane takes off from Chicago O’Hare Airport, flying up at an angle of elevation of 2°, for 410 miles. Then it tilts down and starts to fly directly towards BWI Airport, at an angle of descent of 3°.
Draw a picture. How far does the plane fly on the downward part of its path?
How far is BWI from O’Hare (along the ground)?
In problems 20 through 22, let’s define angle of the sun to mean the angle between the sun’s light rays and the ground. (Note that since the sun is extremely far away, all the light rays are essentially parallel). So, around noon, the angle of the sun is close to 90° and you have a very short shadow:

Late in the afternoon, on the other hand, the angle of the sun is much smaller, and you have a longer shadow:

Just before noon, the angle of the sun is 89°.
How long is the shadow of a 40 ft tall house?
How tall is a building that has a 25 ft shadow?
At 5pm, a 100-foot building has a 40 ft shadow.
Estimate, without using your calculator, the angle of the sun.
Now calculate the angle of the sun.
What’s the angle of the sun if everyone has a shadow that’s 5 times their height?
Give the lengths of the 3 sides of a right triangle, where exactly two of the sides are irrational and one of the angles has a sine of $\frac{1}{2}$.
A dartboard is shaped like a regular hexagon with 10-inch sides. Its vertices are (in this order) A,B,C,D,E,F. You get a point if you hit the target region, rectangle ACDF. What are your chances of getting a point?
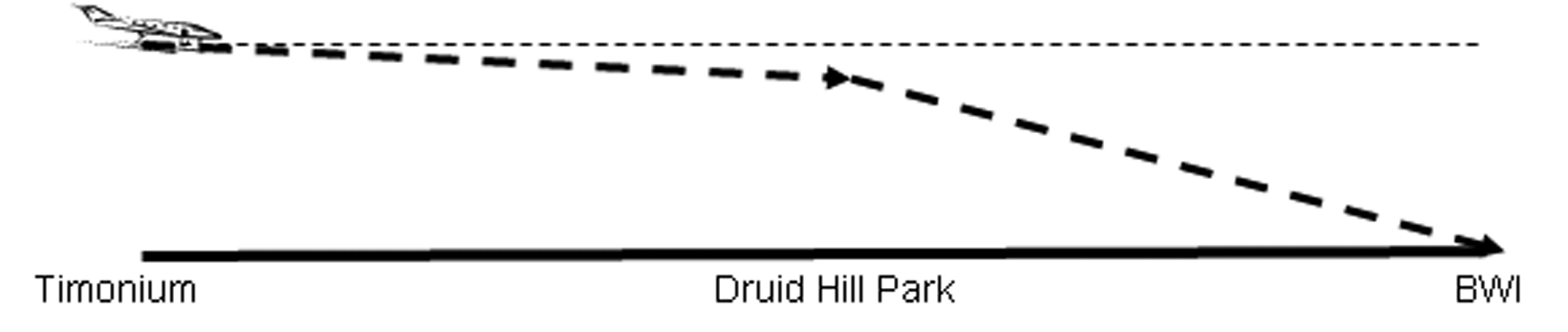
A plane is landing at BWI airport. You start observing the plane when it’s directly above Timonium, which is 15 miles away from the airport. At this time the plane is .55 miles above the ground. It’s flying at an angle of descent of 1°, until it’s above Druid Hill Park, which is halfway between Timonium and BWI. Then the plane changes its angle of descent so that it’s heading directly towards the airport. Find the second angle of descent.
You are kicking a ball off the ground at a wall. You win a point if the ball hits the wall between 4 and 5 feet off the ground. If you’re standing 10 feet from the wall, what’s the range of angles you could kick the ball at, to get the point?
You fold a piece of wire in half, and stand it up on the table on its two ends. The angle of the fold is 48°, and the two ends are 6 inches apart. How long was the wire? (Draw a picture).
Find the missing side length in this triangle.
Your house is 10 miles west of Baltimore, and your friend’s house is 11 miles north-west of Baltimore.
Estimate, without using your calculator, the distance between the two houses. (Hint: what’s the angle between west and north-west?)
How far apart are the two houses?
Starting at your front door, you walk 25 feet forward, then make a slight, 10° turn to the right, and walk 5 more feet. Draw a picture, and find how far you now are from your front door.
Two ants on the ground are 15 feet apart. They are looking up at a balloon hovering up in the air between them. If the first ant looks up at the balloon, the angle of elevation of the ant’s line of sight is 84°. For the second ant, it’s 52°. Draw a picture, and then find the distance of the balloon from each of the two ants.
For the next few problems – visualize - find a new way to see a picture, or figure out an interesting way to split a diagram into pieces, giving you more insight into the problem.
Find the area of this shape:

This letter Z, composed of two rectangles and a parallelogram, is symmetrical (the top part is the same as the bottom part). Find all lengths and angles in the picture.
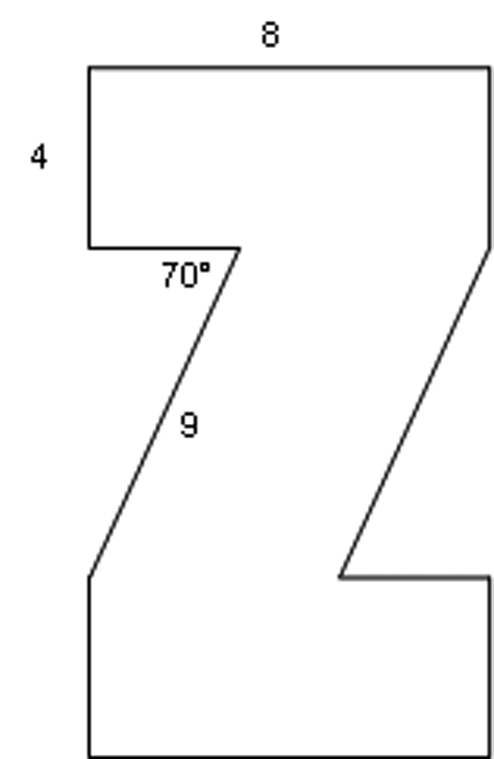
Find X.

This is an equilateral triangle of side length 2 inches. Find a way to split up the triangle so that you can find its area.

This is a regular hexagon of side length 2 inches. Find a way to split up the picture so that you can find its area. (The result in problem 35 would be useful here.)

Back to our regular pentagon of side length 2 inches.

What’s its area?
What’s its height?
Two cars start next to each other. The red car drives 8 miles west, and the black car drives 13 miles north-east. It might be helpful to make this diagram on a grid.
Draw the paths of the two cars. What’s the angle between them?
What’s the distance between the two cars, after they’re done driving?
You are standing near the edge of a cliff (at the top). Your feet are 4.5 feet away from the edge. If you look at the edge of the cliff, your line of sight is at an angle of depression of 53°.
Estimate your height (Pretend your eyes are at the top of your head).
Now determine your height using trigonometry.
In the same line of sight as the edge of the cliff, you see the bottom of a cactus. If the cliff is 95 feet tall, how far away from the base of the cliff is the cactus?
You have a four-sided shape with side lengths 10, 4, 10, and 4 (in inches), and with hinges at all the corners – you can bend it like this:

Let A be the angle indicated in the picture above.a. What kind of quadrilateral is always formed?
What kind of quadrilateral is always formed?
If A=71°, find the area of the quadrilateral.
If A=100°, find the area of the quadrilateral.
What angle A would make the shape have the biggest area? Explain your answer
Line $n$ is described by $y = 2x + 3$. Point $P$ has
coordinates $(4,7)$. Determine the measure of the angle
formed by line $n$ and the line containing point $P$ and the
Don’t use a calculator for this problem.
Divide: $8\frac{2}{3}\div 4\frac{1}{3}$
Simplify: $4 - 2{{( - 1)}^5 - {{( - 2)}^3}} $
Find an equation for the line that goes through the points $( - 10,9)$ and $(5,3)$.
For which values of $x$ does
Evaluate the expression $\frac{{ -
\left| x \right|}}{{\left| { - x} \right|}}$ if $x = 3$, and
then if $x = - 2$.
Can you find a value of $x$ that does not fit the pattern you
see?
Find the measure of the angle formed by a diagonal of a cube and a diagonal of one of the faces of the cube.
A piece of candy looks like a regular hexagon with two isosceles triangles. The piece of candy is 1 inch tall (the top and bottom of the hexagon line up with the top and bottom points of the triangle).

Find all the angles in the picture.
Tinker with the diagram as necessary so that you can find all the lengths in the picture.
Find the exact area of the candy.
This is a perfect star (everything is symmetrical).
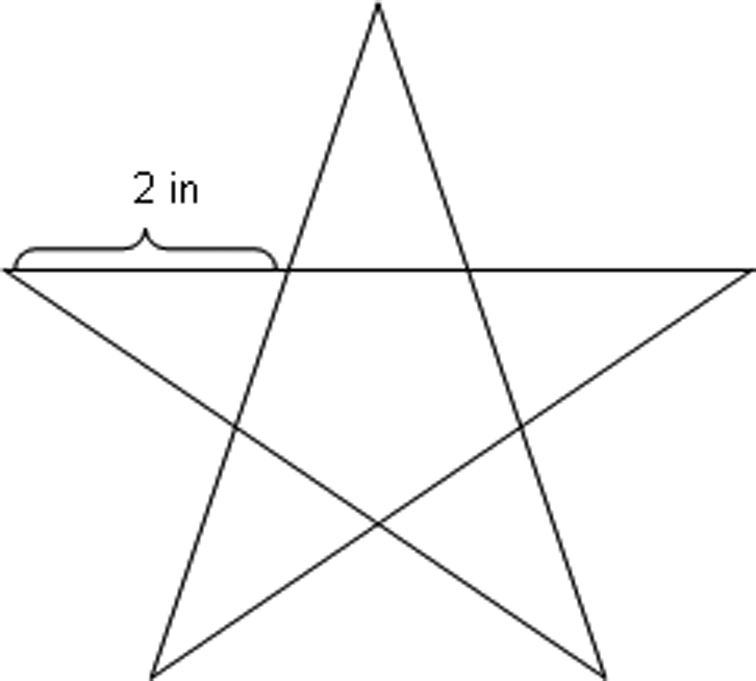
Find all the angles in the picture.
Find all the lengths in the picture.
Find the area of the star.
You throw a tennis ball from a height of 5.5 ft off the ground, and it makes an angle of 35° with the ground when it hits and when it bounces back up. After bouncing up it hits a wall. You are standing 26 feet away from the base of the wall.
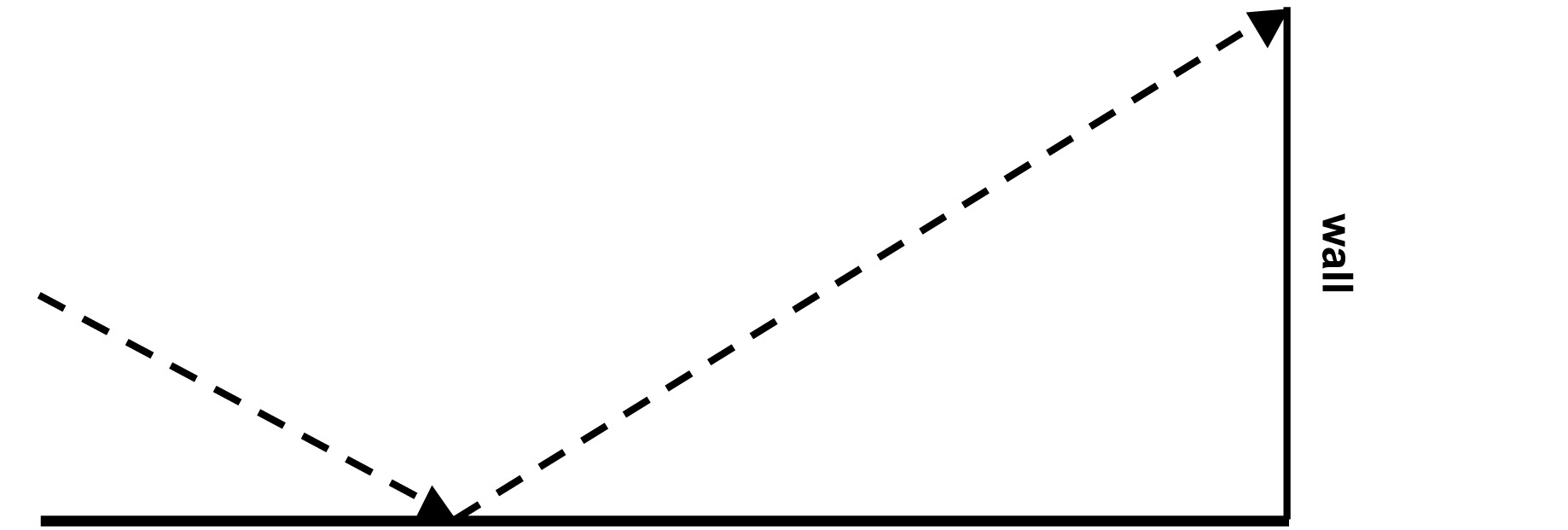
How far away from your feet did the tennis ball bounce?
How high up on the wall did the tennis ball hit?
How far did the tennis ball travel?
A ladder is propped against a wall. The top of the ladder is 19 feet above ground, and the ladder makes an angle of 75° with the ground.
Estimate, without using your calculator, the length of the ladder.
How long is the ladder?
The ladder slides 4 feet down the wall. How far away from the wall is the base of the ladder, after the ladder’s slide?
You have a 20 foot ladder propped against a wall. It makes an angle of 55 degrees with the floor. Then it slides down a little bit. After the slide it makes an angle of 25 degrees with the floor.
How far along the wall did it slide?
How far along the ground did it slide?
Jill is 5.7 feet tall, and Elizabeth is shorter. They stand facing each other. Jill looks down at Elizabeth’s feet, and her line of sight has an angle of depression of 76 degrees. (You can assume people’s eyes are at the top of their heads).
Draw a diagram of the situation with all the information filled in. How far apart are they standing?
When Elizabeth looks up to the top of Jill’s head, her line of sight is at an angle of elevation of 19 degrees. How tall is Elizabeth?
Point $Q$ has coordinates $(5,2)$.
Find the image of $Q$ after it’s been rotated 30 degrees counterclockwise around $(0,0)$.
Find the image of $Q$ after it’s been rotated 30 degrees counterclockwise around $(1,3)$.
Exploring in Depth
Find the missing side length.

The perimeter of the triangle below is 100. Find the lengths of the sides. (Write equations!)
You leave your house, and walk 10 miles north. Then you make a 30 degree turn to the right and walk 8 more miles. Then you make a sharp turn to the right (more than a 90 degree turn) and walk some more, ending up exactly 15 miles due east from your house. How long was this last piece of your walk?
Find X. (You can assume that the two lines that appear to be parallel are indeed parallel).

You are $X$ inches tall. One afternoon, you notice that your shadow got 4.5 inches longer between when you left school (when the angle of the sun was 72°) and when you got home (when the angle of the sun was 68°).
In terms of $X$, how long is your shadow when you leave school?
In terms of $X$, how long is your shadow when you get home?
Find $X$.
A plane is flying east, with an angle of descent of 10°. After flying 43 miles, it turns around quickly and starts flying due west, at an angle of descent of 14°, for $X$ miles – pretty far past where it started. It ends up exactly 18.5 miles away from where it started. Draw a picture, and then find X.
The strangely pointy butterfly below is perfectly symmetrical across the middle, and all the angles that look like right angles are perfect right angles. He is 2 inches across at the widest point, and 1.6 inches tall. Find all the lengths in the picture.

Let line $n$ and point $P$ be as in problem 41: $y = 2x + 3$ and $(4,7)$. Determine the coordinates of the reflection of $P$ over line $n$.
You take a 40 degree sector of a circle (a sector is like a slice of a cake), and cut off the triangle. What’s the area of the piece that’s left, if the radius is 10?

At 5pm one day, you are attempting to measure the height of a mountain. First, you observe that while you are 6 ft tall, your shadow is only 2.5 feet long. Then, you observe that the mountain’s shadow extends 120 ft past the foot of the mountain. Also, the angle at the base of the mountain is 105°. How tall is the mountain?

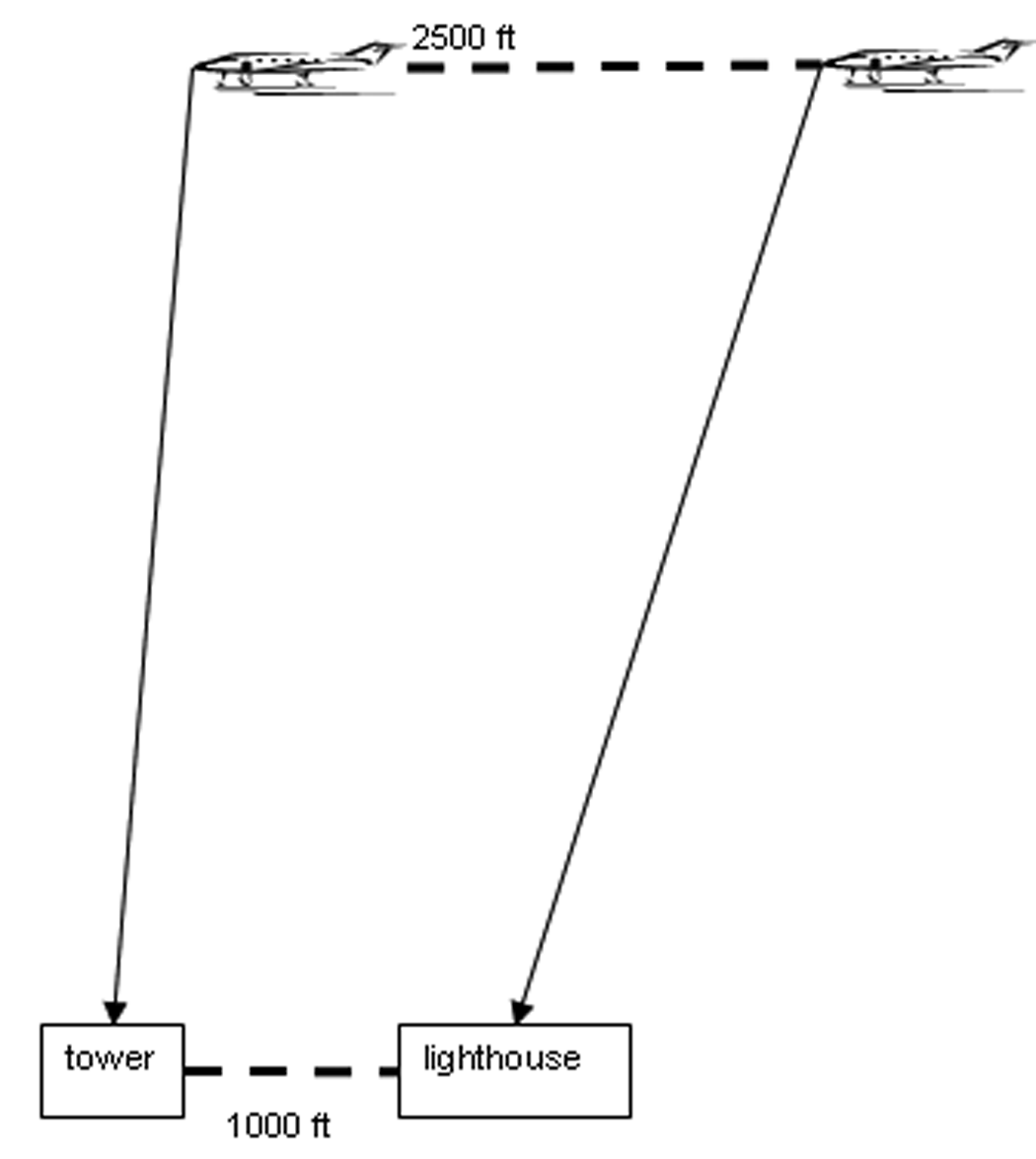
A plane is flying west at a constant altitude. The pilot looks down and sees a lighthouse, and his line of sight is at an angle of depression of 85° - the lighthouse is almost directly below the plane. After the plane flies 2500 more feet forward, the pilot looks down again, this time at an angle of 89°, and sees a tower that he knows to be 1000 feet west of the lighthouse. What is the altitude of the plane? (Note – the picture is not to scale!)
You see the top of a palm tree 14 yards away from you, at an angle of elevation of 40 degrees. Behind the palm, you can tell that there’s a short pine tree. The top of the pine is 20 yards away from you, at an angle of elevation of 10 degrees. How far apart are the tops of the two trees?
This circle has a radius of 8 inches, and the chord AB has a length of 10 inches. Find the arc length of arc AB.

On a hiking trip, you start at point A and hike 5 miles in a direction that’s 4° north of due east. Then, you turn your path slightly, by 10° to your right, and walk until you are directly east of point A where you started.
Draw a diagram of the situation. How long do you have to hike in this new direction before you make it back onto your intended trail?
How much shorter would your path have been, if you just walked straight east instead of up and then down?
Two motion-detector cameras sense an unidentified object hovering in the air somewhere above them. The first motion detector is on the ground, and it registers the object’s location as 8.6 miles away, at an angle of elevation of 80°. The second motion detector is on a tower 2 miles above the ground, and registers the object’s location as 10 miles away at an angle of elevation of 40°.
Draw a diagram of the situation, and find the distance between the two motion detectors.
The area of a regular quadrilateral (a square) where each side is length 1 will of course be ${1^2}$, which is an integer. Do any of the other regular polygons with sides of length 1 have integral area? How about rational area?