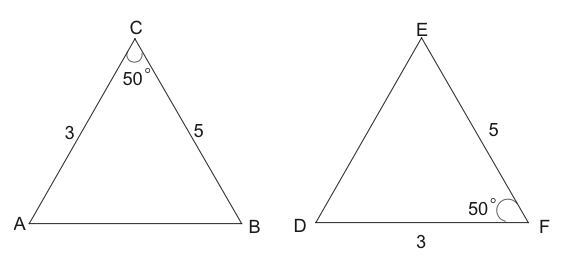
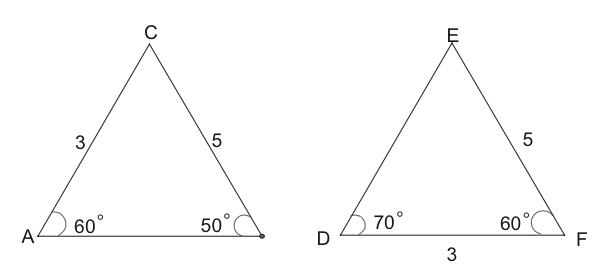
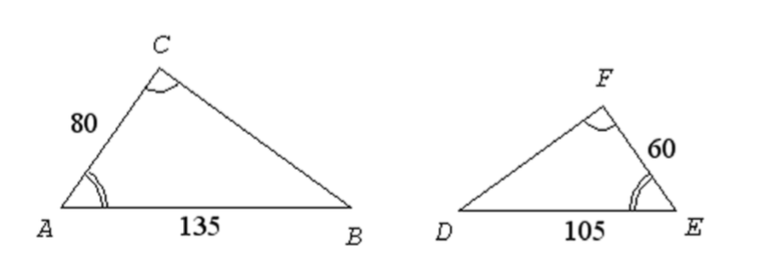
For each pair of triangles shown, say if they must be similar, must not be similar, or if there is not sufficient information to tell. If the triangles are similar, write the similarity statement (with a “$\sim$"), paying attention to the correct order of the letters.



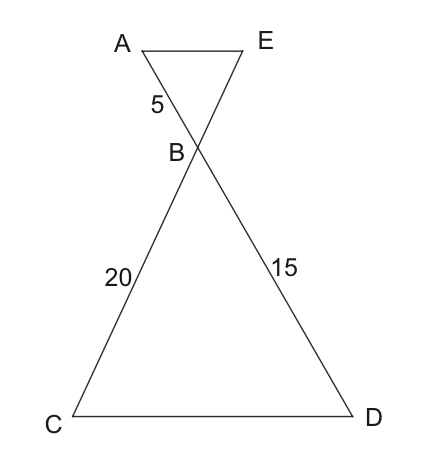
In the figure below, AE is parallel to CD. Why are the triangles similar?
Find all the missing side lengths.
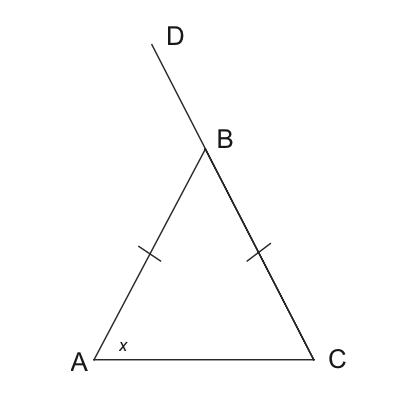
Below is an isosceles triangle with one of its sides extended. If angle A is $x$ degrees, find the measure of angle ABD in terms of $x$.
In triangle ABC, it is given that angle A is 59 degrees and angle B is 53 degrees The altitude from B to line AC is extended until it intersects the line through A that is parallel to segment BC; they meet at K. Calculate the size of angle AKB.
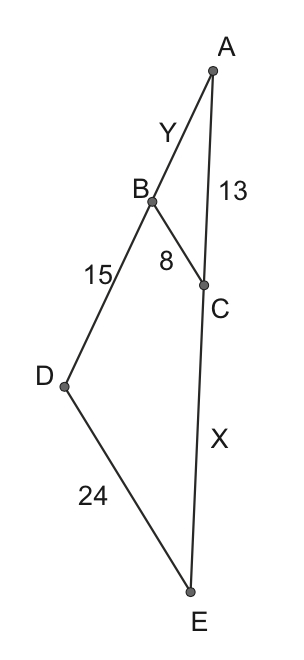
In the picture below, $BC||DE$ . Find $X$ and $Y$.
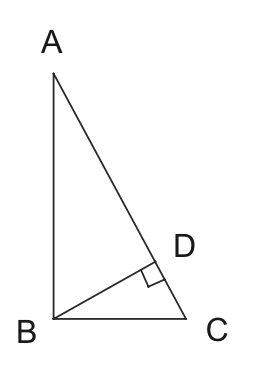
ABC is a right triangle. The altitude to its hypotenuse is drawn, hitting the hypotenuse at point D. $AD = 9$ and $DC = 4.$ Find $x$, the length of the altitude.
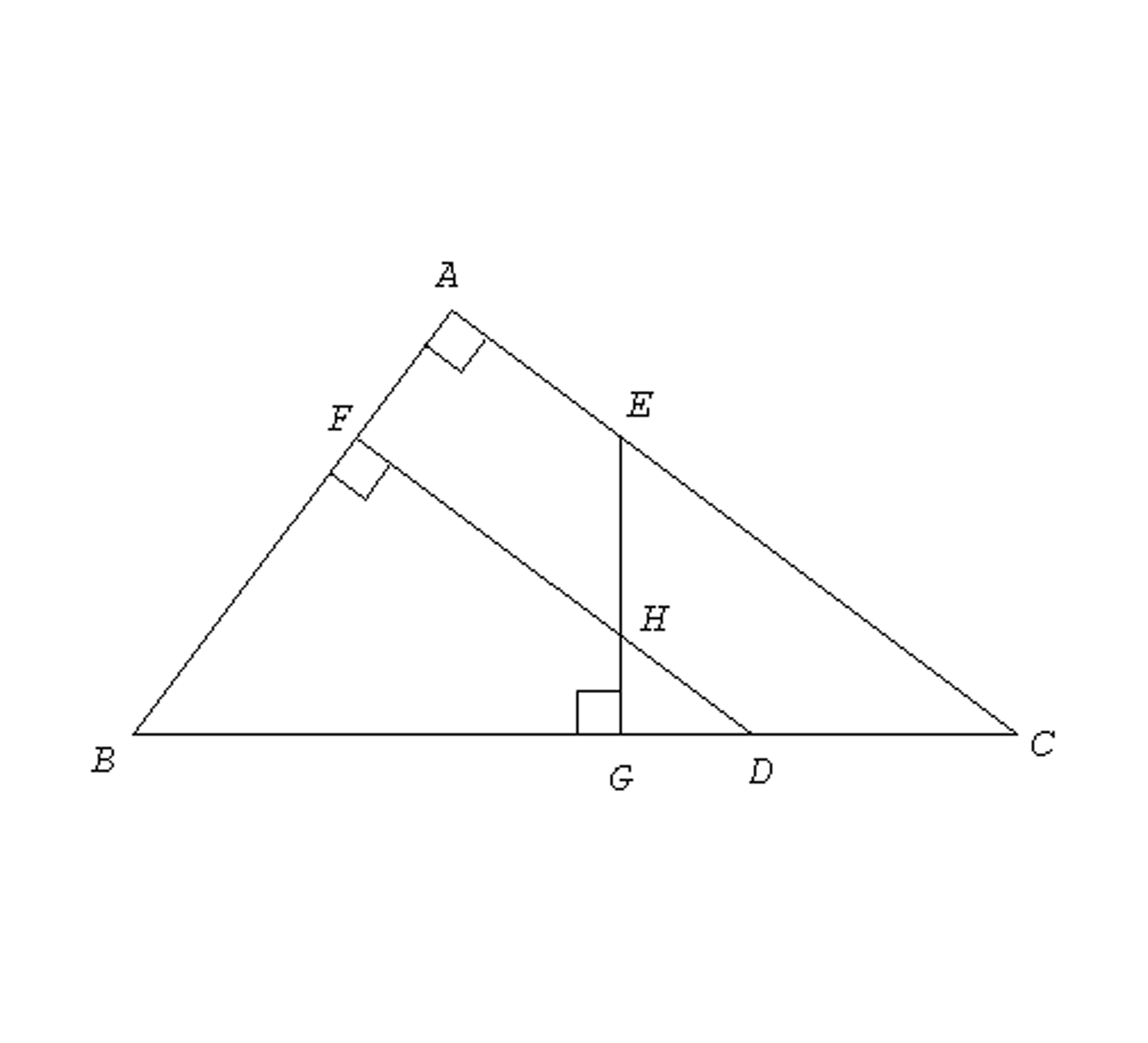
In the figure below, $\angle ACD$ and $\angle BED$ are right angles. Name all the triangles in the figure that are similar to each other, using correct similarity notation.
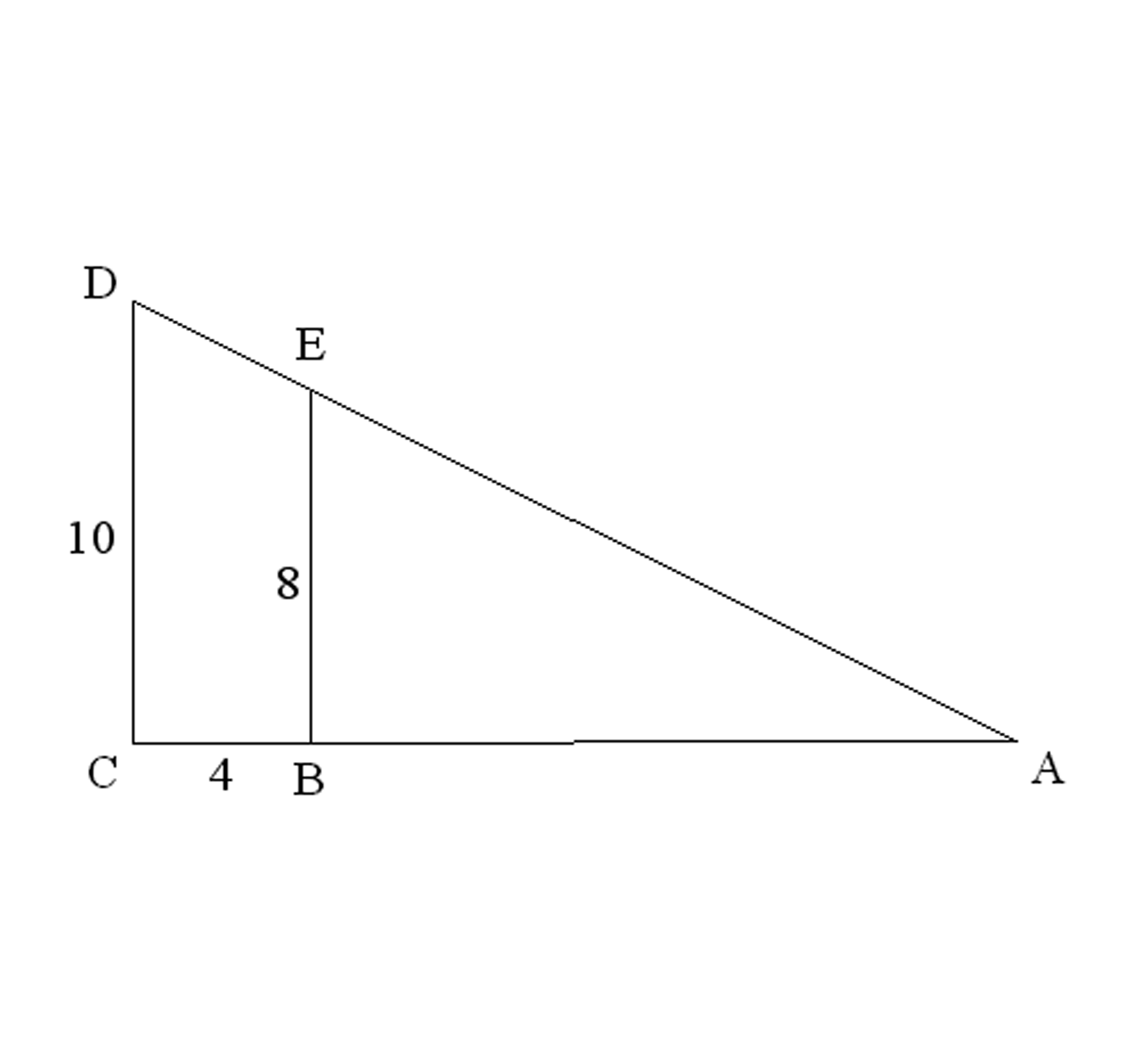
In the figure below, $\overline {BE} \parallel \overline {CD} $, and $\angle ABE$ and $\angle C$ are right angles. Find each of the following.
AB
ED
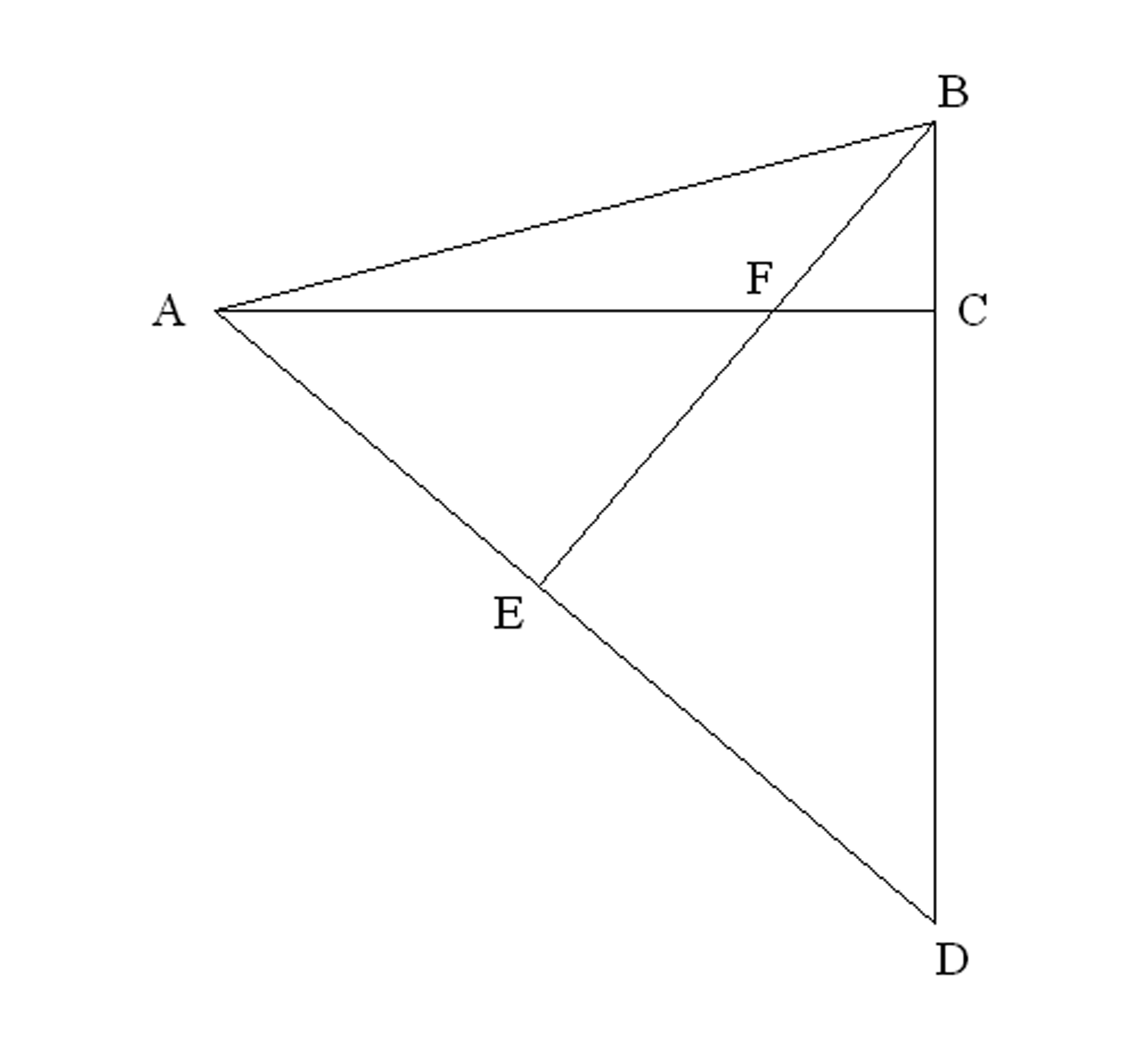
Look carefully at the diagram below
before answering the following questions.
Name as many pairs of similar
triangles as you can. Use correct similarity notation.
If $EC = 5.6$ , $CD = 3$ , $GD = 1.48$, and $FH = 3.75$ , calculate the length of $\overline {BF} $. You must show your work clearly.
What’s wrong with the picture drawn below?
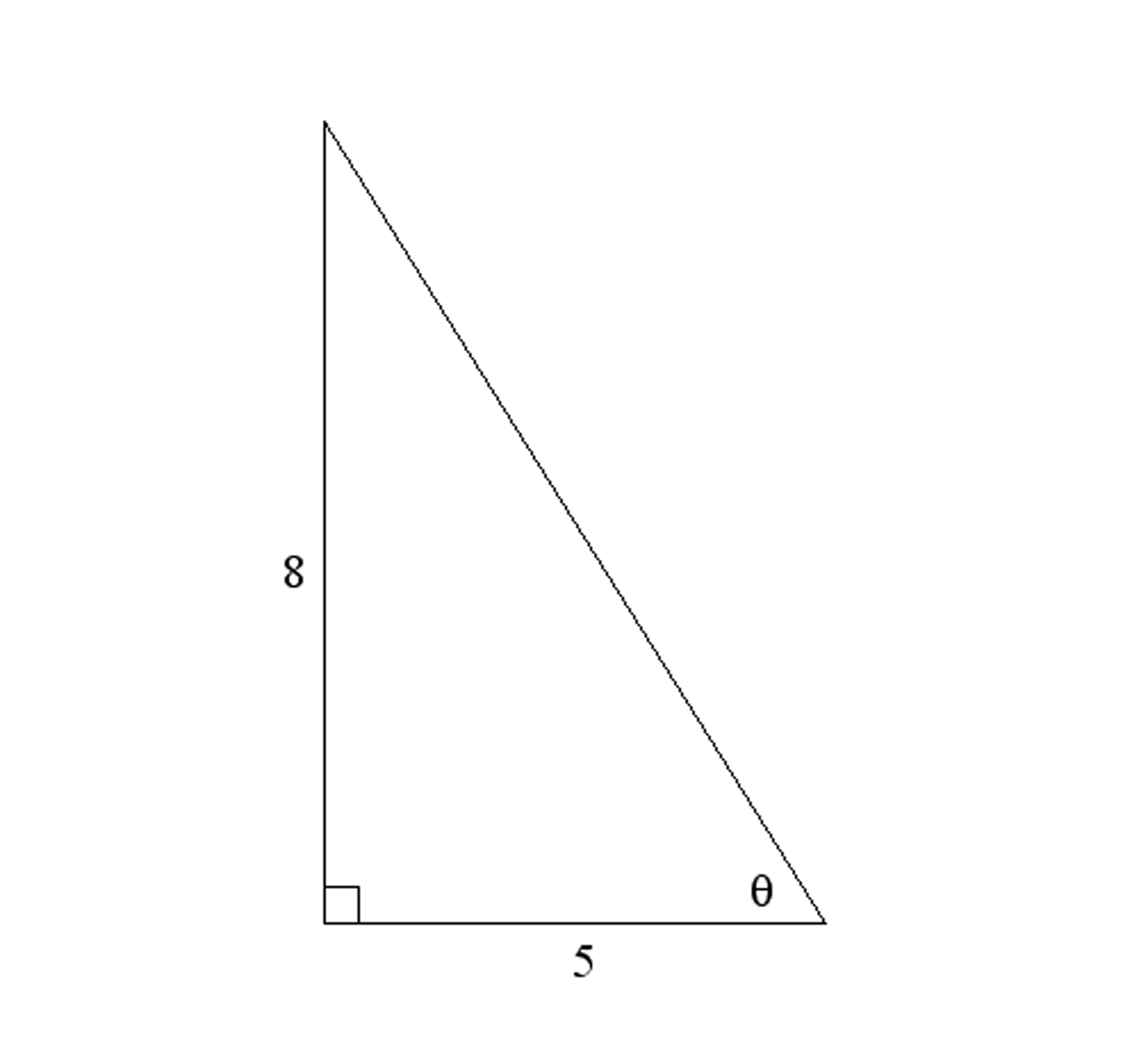
Use the triangle below to determine the values of the following expressions.
The exact length of the hypotenuse. This means don’t approximate its length.
$\sin \theta $
$\cos \theta $
$\tan \theta $
$\sin \left( {{{90}^ \circ } - \theta } \right)$
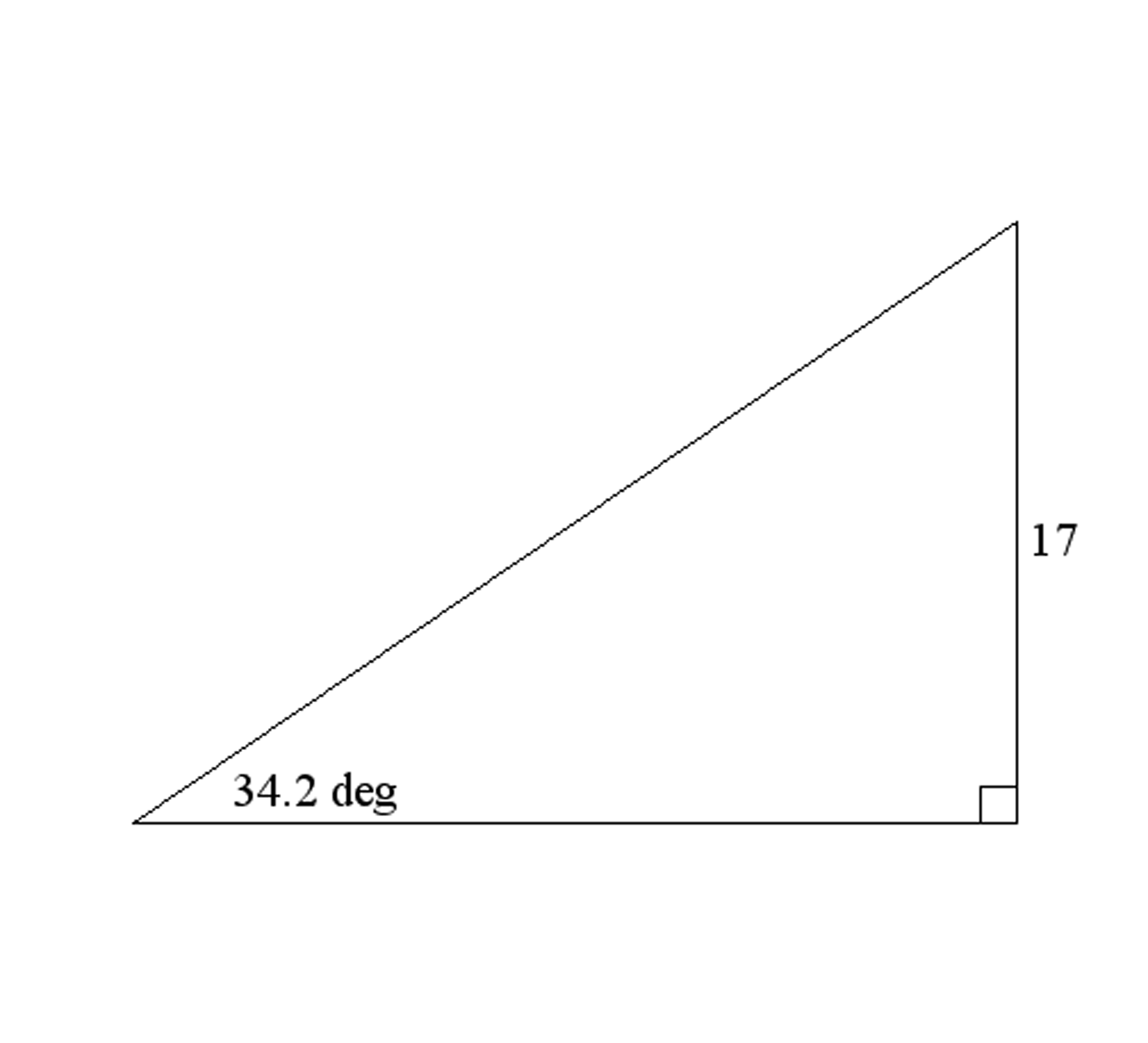
Use trigonometry to calculate the lengths of the unknown sides of the right triangle given below. Show your work.
Recall that the convention for labeling sides and angles
of triangles is to put side $a$ opposite angle $A$, etc.
Find the missing information in each
triangle:
In triangle ABC, $\angle A = 90^\circ ,{\rm{ }}\angle B = 25^\circ ,$ and $a = 18$. Find $b$ and $c$.
In triangle XYZ, $\angle X = 90^\circ ,{\rm{ }}\angle {\rm{Y = 37}}^\circ {\rm{,}}$ and $z = 25$. Find $x$ and $y$.
Why does your calculator give you an error when you try to do $\sin^{-1}(2)$, but not when you do $\tan^{-1}(2)$?
The CN tower in Toronto is the highest tower in the world. You are standing 100 m away from the base of a tower. You can just see the top of the tower when you look up at a 79.7° angle. How tall is the tower?
A student looks out of a second-story school window and sees the top of the school flagpole by angling his line of sight 22° above the horizontal. The student is 18 ft above the ground and 50 ft from the flagpole. Find the height of the flagpole.
Squidward is in a plane that is 160 miles north and 85 miles east of SpongeBob airport.
How far away is the airport?
What direction should the plane fly to go directly to the airport? (Your answer should be very specific and include an angle)
An observer in a lighthouse 350 feet above sea level
observes two ships approaching. The angle of depression to
the first ship is $4^\circ $, and to the second is $7^\circ
$. How far apart are the ships?
What is the perimeter and area of the figure below?
A triangle has sides of length $g$, $g$, and
$\frac{{7g}}{5}$ . Is it a right triangle? Explain.
$\triangle ABC$ is a right triangle with right angle B. A line segment is drawn from angle B perpendicular to $\overline{AC}$. Where it intersects this side mark the point D. Let $BC = 12$ and $DC=11.07692$. Find the area of $\triangle ABC$. Show your work.
A plane flies 500 miles from Boise to Snazziville, then changes direction at Snazziville and flies 840 miles to Dubuque. (see the picture below).
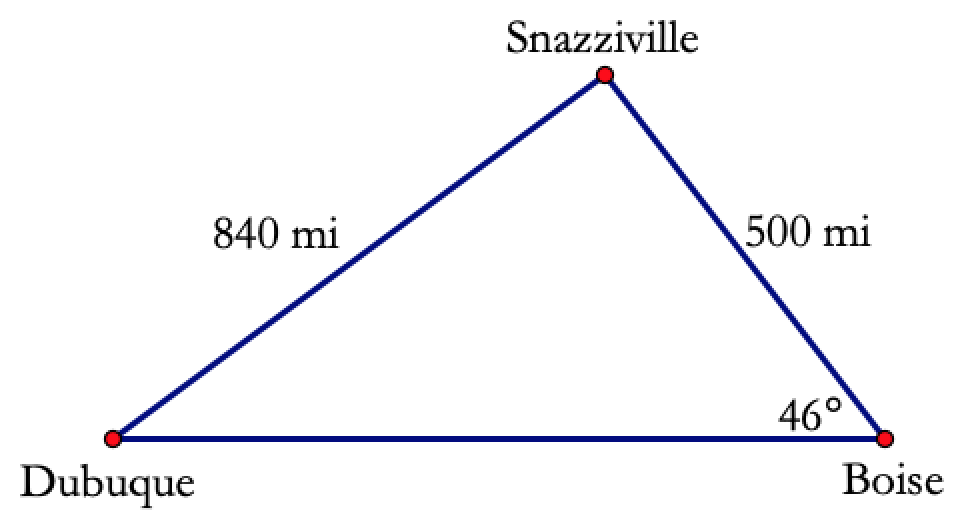
What is the measure of the angle with vertex Dubuque?
How far is it from Boise to Dubuque?
If the plane always flies at 600 miles per hour, how much time was wasted going by way of Snazziville instead of going directly to Dubuque?
Simon and Paula are 30 kilometers apart, and they each spot a religious idol on fire in the distance (see the picture below).
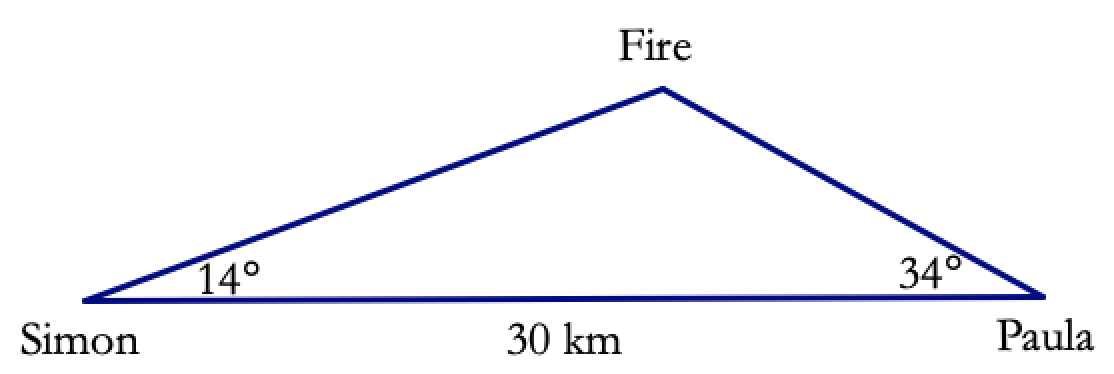
How far are Simon and Paula from the fire?
What is the area of the triangle?
In parallelogram ABCD below, $BD = 12$ , $\angle A = 75^\circ $, and $\angle BDA = 45^\circ $ .
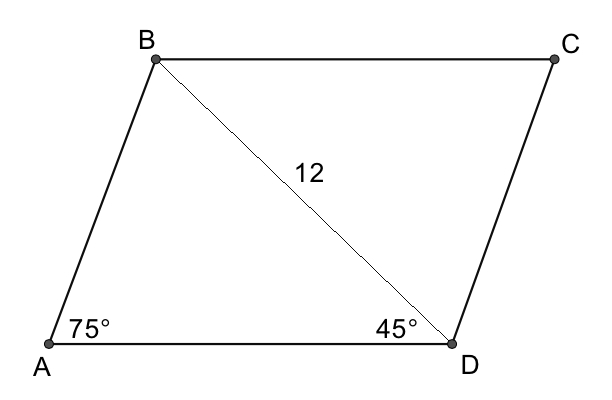
Find AB.
Find the area of the parallelogram.
In the figure below, find x, y, z, AB and BC.
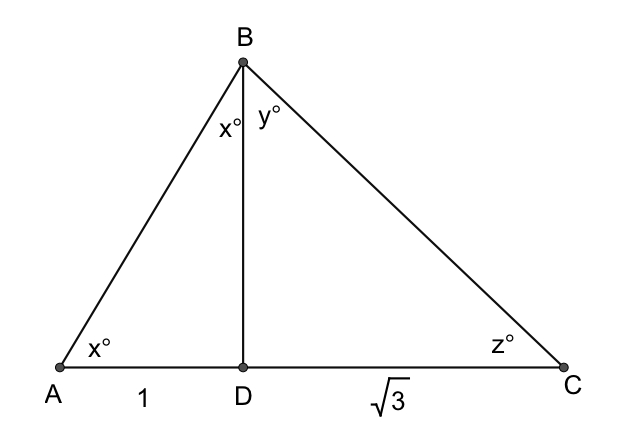
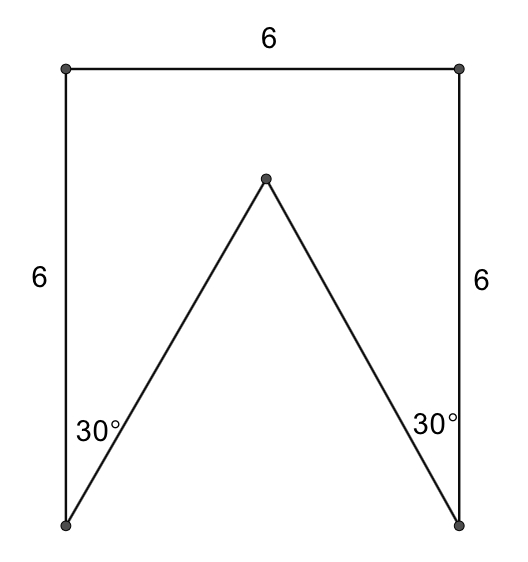
The altitude (or height) of an equilateral triangle is 6. Find the triangle’s perimeter.
The perimeter of a regular octagon is 72.
What is the length of each side?
What is the sum of its angles?
Find the area of the octagon.
A right triangle has a perimeter of 24, and its hypotenuse is three times as long as its shorter leg. Find the lengths of all three sides of the triangle.
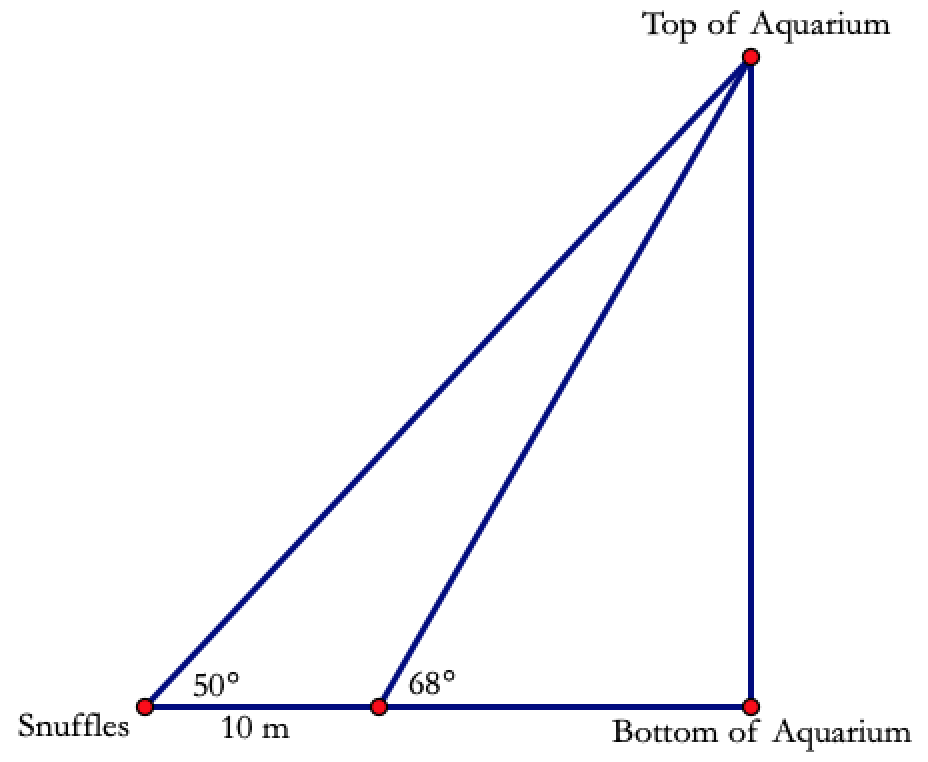
When Snuffles looks up to the top of the Aquarium, he is looking up at an angle of $68^\circ $. When he steps back 10 meters, now when he looks up to the top of the aquarium, he is looking up at only $50^\circ $. Determine the height of the aquarium, and the area of the triangle on the left.
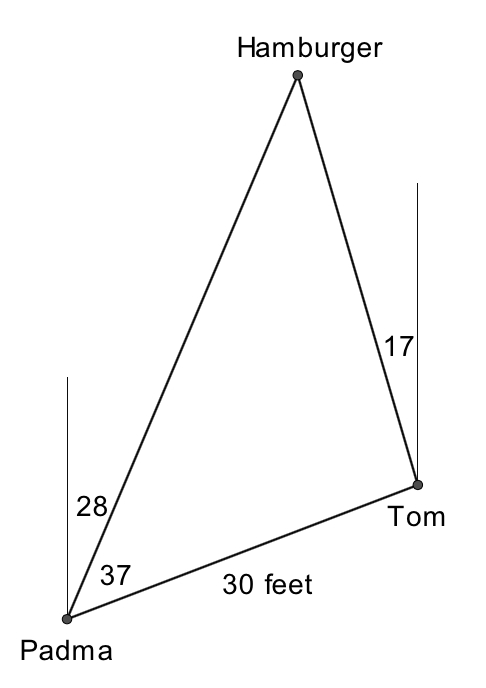
Tom Colicchio and Padma Lakshmi haven’t eaten in 5 days as the food that has been cooked for them hasn’t been fancy enough for them to deign to eat it. By this point, however, they are both starving. As in the picture below, a hamburger appears suddenly. Assuming Padma runs $1\frac{2}{3}$ times as fast as Tom, who gets to the burger first?
In right triangle ACB (where C is the right angle):
If a = 12 and $\angle B = 71^\circ $ , determine the rest of the angles and sides of the triangle.
If, instead, c = 13 and b = 6, determine the rest of the angles and sides of this other triangle.
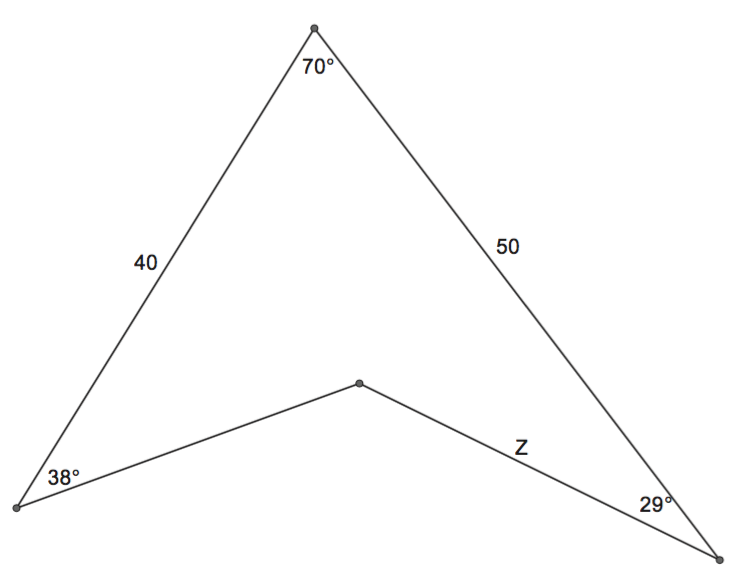
In the diagram below, find Z.
Socrates, the Ancient Greek philosopher, was known for
being a trickster. One day, Socrates claimed to have a
triangle whose lengths were 5, 8, and 10. He also said that
two of the angles in the triangle were ${50^ \circ }$ and
${27^ \circ }$ .
Explain why Socrates’ triangle can’t possibly exist.
Andrew decides to measure the height of a tree by using an idea he learned in class. He takes two poles—one 10 feet long and the other 14 feet long—and walks up to a very tall tree. He places the 14-ft tall pole to the side, walks with the 10-ft pole straight out 36 feet from the tree and plants the pole so that it is parallel to the tree. He then walks along the same line father away from the tree until the line-of-sight from the ground to the top of the 10-ft pole intersects with the top of the tree. He marks this spot on the ground and measures from it to the base of the 10-ft pole. This distance is 6 feet. He then takes the other pole—the 14-ft one—and walks in the opposite direction from the 10-ft pole until he’s 40 feet from the tree. He plants the 14-ft pole so that it is parallel to the tree. He then walks along the same line farther away from the tree until the line-of-sight from the ground to the top of the 14-ft pole lines up with the top of the tree. He marks this spot on the ground and measures from it to the base of the 14-ft pole. This distance is $d$ feet. (You’ll notice that I’m not telling you what this distance is. Heh, heh, heh!) Assume the ground is level throughout the entire area that Andrew is measuring.
Draw a diagram that shows the situation and all of the key measurements.
Determine the height of the tree. Show your work.
Determine what $d$ is. Show your work.
Did Andrew need both poles to measure the height of the tree? Explain.
The circle below has a circumference of $48\pi $. The length of the arc AB is 12.
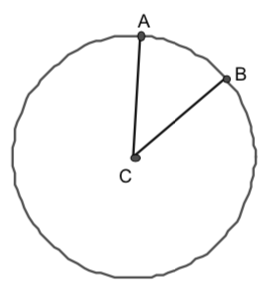
What is the radius of the circle?
What is $\angle ACB$ ?
If Josephine removed sector ACB (that is, the “piece of pie”) from the circle, what would the area be of what was left?
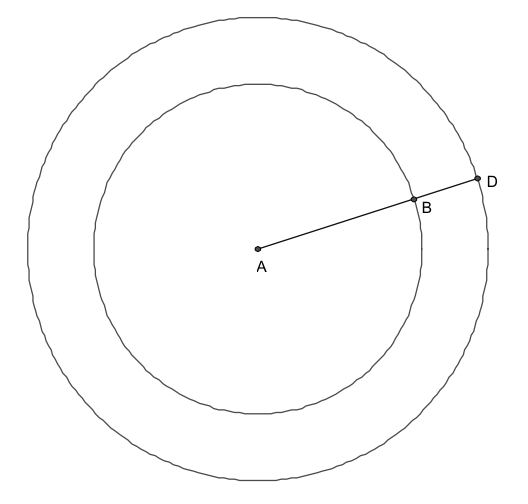
If the area between the circles above is $51\pi $, and $AD = 10$, find $BD$.
If, alternatively, the area between the circles is $24\pi $ and $BD = 2$, find $AB$.