Flu Season, Again.
One of the most unpleasant aspects of going to school is that when a few people get sick, they can transmit their illness to others very easily, and as a consequence most of the school can end up “catching” it.
Epidemiologists, when faced with the spread of a disease, try to predict how quickly people will be infected by coming up with equations that seem to fit the data well. One reasonably accurate equation is called the logistic model, and is based on the following idea. Let $I$ stand for the number of people already infected and $N$ stand for the number who are not infected. Then the rate at which the disease is spreading is proportional to the product of $I$ and $N$. For the sake of simplicity let’s call this product the “disease quotient” of $DQ$. Let’s assume, also, that the $DQ$ is exactly equal to the product of $I$ and $N$. The $DQ$ is, therefore, a measure of how quickly the disease is spreading: the higher it is, the more people get infected that day.
How would you expect $DQ$ to change while the disease is spreading? At what point during the spread of the disease would the disease spread most quickly?
Development
Let’s look at a specific case — a local high school with 400 students.
What is the $DQ$ when no students are infected? When 1 student is infected? When 70 students are? When 300 are infected?
Write an expression describing the $DQ$ if one knows the number $x$ of students that are infected.
Rewrite the equation in Problem 2 so that it’s in the form $DQ = ax^2 + bx + c$. What are $a$, $b$, and $c$ in your equation?
Any equation that can be written in the form $y = a{x^2} + bx + c$, where $a \ne 0$, is called a quadratic equation. In this lesson we will be looking at some algebraic tools that can be used to manipulate these equations so as to learn more about how the solutions of such an equation behave.
Determine the number of people who are infected if $DQ = 0$. You should get two answers.
Pick one of your answers from problem 4 and explain why, without talking about the disease quotient or the number infected or not infected, it must be a solution to the equation $x(400-x) = 0$.
Think carefully about your answers to Problem 4 and how they solve the equation given in Problem 5. Now, explain why 2 and -3/4 are solutions to the equation $\left( {4x + 3} \right)\left( {x - 2} \right) = 0$.
Solve each of the following equations.
$x\left( {x + 10} \right) = 0$
$\left( {x - 3} \right)\left( {x + 2} \right) = 0$
$\left( {x + 5} \right)\left( {x + 7} \right) = 0$
$- 2\left( {x - 4} \right)\left( {x + 9} \right) = 0$
${\left( {x + 1} \right)^2}\left( {3x - 1} \right) = 0$
$\left( {4x + 5} \right)\left( {x - 3} \right)\left( {x + 1} \right) = 0$
What must be true about $A$ or $B$ if $A \cdot B = 0$? Can the same thing be said if $A \cdot B = 8$?
In Problem 8 you’re being asked to conjecture a very important theorem of mathematics that is often referred to as the Zero Product Property — anytime you have a product, then it can equal zero only if at least one of its factors is zero. This is a very powerful theorem in situations in which we can write an equation in the form ${\rm{BLAH}} = 0$, where BLAH can be written as a product. So, it seems useful here to focus on how to write expressions as products, don’t you think?
There is a way to rewrite expressions ${x^2} + 7x + 10$ as a product of two expressions, so that it looks like $(x+\ldots)(x+ \ldots )$. You may have seen this technique before: it is called factoring.
Working on your own or with your peers, factor ${x^2} + 7x + 10$. When you have an answer, look carefully at your factored form of the expression and how it relates to the original expression.
Solve the equation ${x^2} + 7x + 6 = 0$.
Solve each of the following equations by factoring.
${x^2} + 3x + 2 = 0$
$x^2 + 8x + 12 =0$
$x^2 + 20x + 64 =0$
${x^2} + 6x + 9 = 0$
${x^2} + 5x - 14 = 0$
In Problem 11 Part e, you needed to resort to negative numbers in order to factor the expression. Try to notice number patterns you see in the original expression and its factored form. Then try the following problems.
Factor each of the following expressions.
${x^2} + 4x - 45$
${x^2} - 5x - 36$
${x^2} - x - 42$
Factoring is not a process reserved for expressions like ${x^2} + 6x + 8$, but can also be done on expressions like $3{x^2} + 7x$. In essence, factoring is a process devoted to reversing distribution: can we rewrite $3{x^2} + 7x$ so that its factored form, when multiplied out, would give us back $3{x^2} + 7x$?
Factor $3{x^2} + 7x$. Check your work by doing the distribution.
Solve each of the following equations by factoring.
$2x - 5{x^2} = 0$
$6{x^2} + 4x = 0$
$5{x^3} - 12{x^2} = 0$
${x^3} - 8{x^2} + 16x = 0$
Practice
Kyle is managing an upcoming concert at school and is concerned about the income generated by the concert just through ticket sales. Over the years he has come to realize that when the price of the ticket increases, the number of people willing to attend goes down. He knows that all 360 students will attend if the concert is free, but for each $1 increase in the price of the ticket, 20 fewer students will attend.
How many students will attend if Kyle charges \$2 per ticket? How many if he charges \$5?
What income will Kyle generate if he charges \$2 per ticket? What if he charges \$8?
Write an expression for the income $I$ generated by the concert when the price of the ticket is $p$. Is this a quadratic equation?
Set the expression in Part c equal to zero and solve this equation. Explain the meaning of the solution in the context of the problem situation.
Factor each of the following expressions.
${x^2} + 16x + 15$
$6x - 10{x^3}$
${x^2} + 3x - 28$
${x^2} - 7x - 18$
Solve each of the following equations by factoring.
${x^2} + x - 20 = 0$
$5x^4 + x^3 =0$
$x^3 + 5x^2 - 14x =0$
Going Further
Graph the equation you came up with in Problem 2 on a calculator. (If you have trouble seeing the graph, take a look at the values you computed in Problem 1.)
Use the graph in Problem 18 to determine when the $DQ$ is 25600. Explain why both of your answers make sense in terms of the spread of a disease.
How many people have been infected if $DQ = 20000$?
Determine the maximum $DQ$. How many people are infected at this point?
Explain how you can use your answers to Problem 19 to solve Problem 21. Could you have used the answers from Problem 20 to solve problem 21?
The two numbers that you calculated in Problem 21 serve as the coordinates of a specific point on the graph of the $DQ$ equation. The graph of the equation is called a parabola, and the point that you calculated in Problem 21 is called the vertex of the parabola. The vertex can be thought of as the point where the parabola turns.
The graph of $DQ = x(400-x)$ is symmetric over a vertical line. Write an equation for this line.
An answer to Problem 15 Part c could be $I = p\left( {360 - 20p} \right)$. Graph this equation on your calculator, then write an equation for its line (or axis) of symmetry. You might look at Problem 15 Part d to help you solve this problem.
The graph of $I = p\left( {360 - 20p} \right)$ intersects the $p$-axis. What are the coordinates of the intersection(s)?
You may recall that the points you found in Problem 25 are
referred to as the
Determine the vertex of the graph of $y = \left( {x + 5} \right)\left( {x - 4} \right)$ without using the graphing or table features of your calculator.
Determine the vertex of the graph of $y = x^2 - 12x + 27$ without using the graphing or table features of your calculator.
Describe a process for determining the exact coordinates of the vertex of the graph of $y = {x^2} - 5x - 14$. At no time can the process rely on a graph of the equation.
Practice
Let $y = x^2 - 3x - 54$. Solve the following problems without using the table or graphing features of your calculator.
Determine the exact coordinates of the $x$-intercepts of the graph of the equation.
Determine the exact coordinates of the vertex of the graph.
Write an equation for the axis of symmetry of the graph.
The points $\left( {4,10} \right)$, $\left( {8,25} \right)$, and $\left( {26,10} \right)$ are on the graph of a parabola. Write an equation for the parabola’s line of symmetry.
If the $x$-coordinate of the vertex of a parabola is $\frac{3}{7}$ and one of its roots is $\frac{5}{6}$, what is its other root? (Answer as a fraction.)
For each equation below, determine the exact coordinates of the vertex of the graph.
$y = {x^2} + 6x + 8$
$y = 2{x^2} - 5x$
$y = - 2\left( {{x^2} - x - 12} \right)$
Problems
The King of Prussia wishes to make a magnificent rectangular temple. He has just enough gold to adorn a perimeter of 98 meters. The king wishes his temple to have the greatest possible area, so that as many people can stand in it as possible.
How can one express the relationship between the length, width and perimeter of the temple in an equation?
How can one express the relationship between the length, width and area of the temple in an equation?
By using your answers to Parts a and b, write an expression that allows one to compute the area in terms of the length of the temple alone.
What length of the temple allows the most people to fit inside?
For religious reasons, the King of Prussia built a temple that was 18 meters long instead; it only let in $P%$ of the people that the “ideal” temple you computed in Part d would have. What is $P$?
The 9th grade is selling tickets to a Rock-Paper-Scissors tournament. Top-secret research has shown that the number ($N$) of high school students who are willing to enter the tournament is highly dependent on the entry fee ($P$). If there were no entry fee, 200 people would enter the tournament; for every dollar the entry fee is above \$0, 50 fewer people will enter.
Write an expression for the number of students ($N$) entering the tournament in terms of the entry fee ($P$).
If the entry fee is $\$3.50$, how many tickets will be sold? Also, how much money will the 9th grade take in as income ($I$)?
Write an equation for $I$ in terms of $N$ and $P$.
Using part a, now write an equation for $I$ in terms of $P$ alone.
What entry fees would produce zero income for the 9th grade?
If the 9th grade wants to make the most money, what should the entry fee be? How much income would the 9th grade then make?
So far you haven’t been asked to factor an expression of the form $a{x^2} + bx + c$, where $a \ne 1$ or $0$.
For example, how would you factor $2{x^2} + 3x + 1$?
Now try factoring $2{x^2} + 7x + 6$.
Use your understanding of Parts a and b to factor each of the following expressions.
- $3x^2 - 2x - 8$
- $2{x^2} - 10x + 12$
- $-2x^2 + 10x - 12$
- $4{x^2} + 4x - 15$
Come up with values for $a$ and $b$ so that $\left( {x + a} \right)(x + b) = {x^2} - c$, where $c$ is some unknown constant.
(Continuation of Problem 36) Factor each of the following expressions, if possible. Note that each of these expressions could be called a difference of squares.
${y^2} - 9$
${x^2} - 100$
${x^2} - {b^2}$
${n^4} - 16$
${x^2} + 25$
${w^2} - 49{x^2}$
Solve each of the following equations.
${x^2} - 2x = 8$
$3{x^3} + 11{x^2} - 4x = 0$
${x^2} = 144$
${r^2} - 9 = 8r$
$\left( {x + 6} \right)\left( {x - 2} \right) = 9$
${x^2} + 4.5x + 3.5 = 0$
$x + \frac{x}{{x - 2}} = \frac{2}{{x - 2}}$
Let ${x^2} + 15x - 324 = 0$.
Find the sum of the solutions and the product of the solutions.
A quadratic equation ${x^2} + bx + c = 0$ has two solutions that have a sum of 2 and a product of -143. Find $b$ and $c$.
$f$ is a function that takes a number, subtracts the square of the number, and then adds 30.
Write a formula $f(x)$= …
What is the largest value that $f$ can output?
25 is a perfect square since $25 = 5 \cdot 5$. Find $d$ if $4{x^2} + 12x + d$ is a perfect square.
Don’t use a calculator for this problem.
Solve for $x$: $\frac{6}{7} = \frac{{33}}{x}$
Evaluate $- {(3)^2} + {( - 3)^2}$
Find an equation for the line that goes through the points $( - 5,4)$ and $(5, - 2)$.
Solve the inequality $- 4x + 13 < x + 3$
Try to make all the numbers from 1-10 by using basic mathematical operations on four 4’s. For example, to make the number 1 you could do $(4 - 4) + (4 \div 4)$.
$\pi $ is approximately 3.141593. Without using a calculator determine whether ${\pi ^2} - 7\pi + 12$ is negative, positive, or zero.
Graph $y = {x^2} + 4x + 7$ on your calculator. Make sure to choose a WINDOW for your calculator that will show the basic shape of the graph.
Explain why the algebraic methods you know don’t seem to help in determining the exact coordinates of the vertex of the graph.
Calculate the $y$-intercept of the graph of the equation.
Now, use your understanding of the symmetry of the graph and the value of the $y$-intercept to determine another point on the graph.
Calculate the exact coordinates of the vertex of the parabola.
Calculate the exact coordinates of the vertex of the graph of $y=-x^2 - 9x + 12$.
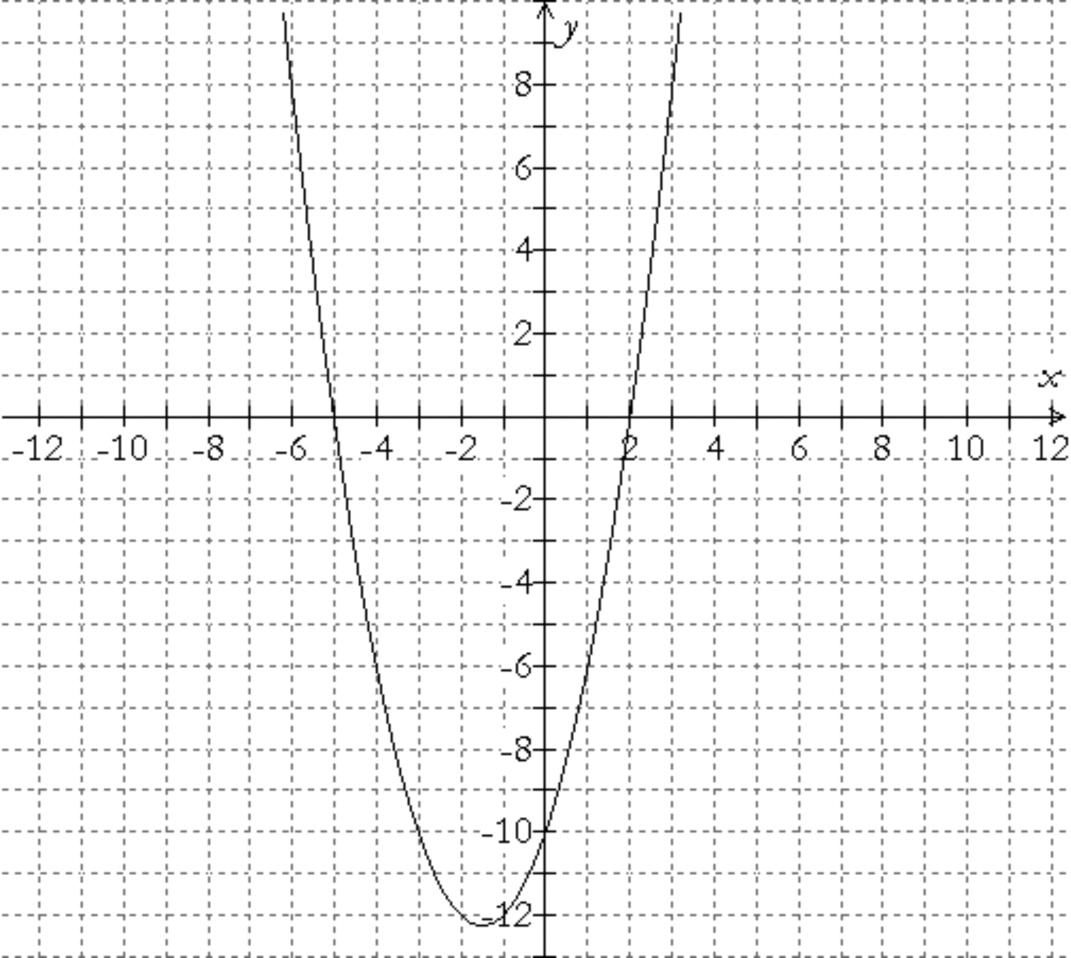
Write an equation for the graph of the parabola given below.
You are selling candy for a price of $p$ dollars per candy bar. 100 people want candy if it’s free, but every time the price goes up by a dollar, 3 fewer people want candy.
Write an equation for $n$ (the number of people who want candy) in terms of $p$.
The government charges a candy tax of $\$1.50$ per candy bar. So when someone buys a candy bar, $\$1.50$ of what they pay goes to the tax. Write an equation for how much you earn for selling one candy bar, if you charge a price of $p$.
Write an equation for $M$, the total amount of money you make, if you charge price $p$. Make sure $M$ is just in terms of $p$.
Without graphing on your calculator, find the maximum amount of money you can make.
Determine a value for $p > 0$ that would make no sense in the context of this problem. Explain why.
Determine the values of $p > 0$ that would lead you to earning zero money.
When Alyssa kicks a football, its height (in feet) as a function of time (in seconds)can be written $h(t) = - 16{t^2} + 40t$.
When will Alyssa’s football hit the ground?
Find the maximum height it will reach.
Hickory, Hunk, and Zeke are building a rectangular pigpen. One side of the pen will be the wall of a barn, and the other three will be made of the 1000 feet of fencing they have.
Draw a picture of the situation.
Write a formula for a function, $A(x) = ...$ that outputs the area of the pen when one of the sides perpendicular to the barn has length $x$.
What value of $x$ should the farmhands choose if they want the pigs to be able to roam over the largest area possible?
Without using the graphing or table features of your calculator, determine the exact coordinates of three solutions to the equation $y=x^2 - 5x - 24$ that would allow you to sketch a reasonable graph of the equation. Why did you pick these three solutions?
Exploring in Depth
For what values of $n$ is $\left( {{n^2} - 3n - 4}
\right)\left( {{n^2} + 8n + 2} \right)$
$ \quad = \left( {5n + 12}
\right)\left( {{n^2} - 3n - 4} \right)$?
You learned how to factor ${x^2} - 1$, but is there a way of factoring ${x^3} - 1$, ${x^4} - 1$, or ${x^{99}} - 1$, for that matter?
We multiply $x - 1$ by $x + 1$ in order to get ${x^2} - 1$. What should we multiply $x - 1$ by in order to get ${x^3} - 1$?
What should we multiply $x - 1$ by in order to get ${x^4} - 1$? How about in order to get ${x^7} - 1$?
${x^4} - 1$ can also be seen as a variation on the expressions in Problem 37. Use this fact to figure out how to factor ${x^3} + {x^2} + x + 1$.
The expression $x - 9$ can be factored in the same way that you factored a difference of squares. Come up with this factoring. Is it true that $x - 9$ equals this factoring for all values of $x$? Explain.
What, if any, integer values of b are there such that
${x^2} + bx + 71$ is factorable? And, more generally, if
${x^2} + bx + c$ is factorable, what can you say for sure
about $c$? about
Solve the following inequalities by using algebra and some number sense.
$\left( {x - 3} \right)\left( {x + 5} \right) \le 0$
$x^2 + 9x + 14 > 0$
$- {x^2} \le x - 42$
$x\left( {x + 3} \right)\left( {x - 2} \right) \ge 0$