Introduction
In Lesson 1 you investigated how to solve quadratic equations like $5\left( {x + 3} \right)\left( {x - 7} \right) = 0$ or $x^2 - 3x - 28 = 0$. You can use the Zero Product Property to solve the first equation, but you’ll need to factor (reverse distribution) the second equation before you can use that property to solve this equation. It’s really nice, in fact, when you can use factoring as a way of transforming an equation into another form that is easier to analyze. Unfortunately, you also saw a few equations that did not readily yield to factoring. Below are some equations of this type:
- ${x^2} + 4x + 2 = 0,$
- ${x^2} - 6x + 6 = 0,$ and
- ${x^2} + 10x - 20 = 0$
Notice that had these equations initially been derived from the equations shown below —
- $y = {x^2} + 4x + 2,$
- $y = {x^2} - 6x + 6,$ and
- $y = {x^2} + 10x - 20$
—you would not be able to use factoring as a way of determining the exact values of the $x$-intercepts. You would be able to approximate them with your calculator but never get the exact values for them. You actually do know a way — a process — of solving this problem, however. Let’s take a look at a process that will get you the exact values.
Development
There are two values of $x$ that satisfy the equation ${x^2} = 9$. What are they? These are called the solutions of the equation.
The two numbers you found in Problem 1 are each called a square root of 9.
What are the solutions to ${x^2} = 49$? What are the square roots of 49?
What are the solutions to ${x^2} = 50$? What are the square roots of 50?
If your answers to problem 3 were 7.071067812 and -7.071067812 (or shorter versions of one or both of these numbers) then you did not find the exact solutions. These numbers are approximations of the square roots of 50.
Explain why $7.07106781^2$ cannot equal 50.
Given your answer to Problem 4, then, you may wonder why your calculator indicates that the square of 7.071067812 is 50. Your calculator does this because it cannot hold onto enough digits to show you what this squared number actually is. A more powerful calculator could show you that ${7.071067812^2} = 50.000000001902467344$. Pretty close to 50, but not quite! The fact is that there is no way to write down the exact value of the positive square root of 50 by using decimal notation.
When we want to indicate the exact solutions to the equation ${x^2} = 50$, or the exact square roots of 50, we just write $\sqrt {50} $ to indicate the positive square root of 50 and $- \sqrt {50} $ to indicate the negative square root of 50. Keep this in mind when you’re being asked to determine the exact solutions to an equation and you need to find square roots in order to do this.
Find the exact solutions to each equation.
${x^2} = 16$
${x^2} - 20 = 0$
$(x-2)^2 = 9$
If you weren’t sure what to do in Problem 5 Part c think
about replacing the
Find the exact solution to each equation.
${\left( {x + 3} \right)^2} = 10$
${\left( {x - 6} \right)^2} - 25 = 0$
${\left( {x + 1} \right)^2} - 35 = 0$
${\left( {x - 10} \right)^2} + 45 = 56$
At this point you should have a pretty good idea about how to solve quadratic equations that are in the form ${\left( {x - h} \right)^2} - k = 0$. So, if you can take an equation like $${x^2} + 4x + 2 = 0$$ and rewrite it in the form $${\left( {x - h} \right)^2} - k = 0$$ Then you would be able to solve the original equation since you know how to solve an equation in this last form. So, let’s figure out how to get a quadratic equation of the form ${x^2} + bx + c = 0$ into the form ${\left( {x - h} \right)^2} - k = 0$.
Complete the table below. The first row has been filled in for you so that you have an idea of what to do.
|
Form V |
Expanded and simplified version of Form V |
|
${\left( {x - 4} \right)^2} - 22 = 0$ |
${x^2} - 8x - 6 = 0$ |
|
${\left( {x - 7} \right)^2} - 39 = 0$ |
|
|
${\left( {x - 5} \right)^2} - 17 = 0$ |
|
|
${\left( {x + 2} \right)^2} - 2 = 0$ |
|
|
${\left( {x + 3} \right)^2} - 5 = 0$ |
|
|
${\left( {x + 9} \right)^2} - 20 = 0$ |
Look carefully at each equation in the right column of the table in Problem 7 and compare it to its corresponding equation in the left column of the table. Look at one row at a time and see if you can pick up on any patterns between the equation on the right and its partner on the left. Once you have come up with some patterns try to use one or more of them to rewrite the equation below so that it is in the form ${\left( {x - h} \right)^2} - k = 0$ (Form V in the table above).
${x^2} + 8x + 1 = 0$.
Once you have rewritten the equation in Problem 8 solve it the same way that you solved the equations in Problem 6. Check your answers in the original equation to make sure that they work.
The process of adding a constant to the terms ${x^2} + bx + c$ so that the resulting expression can be factored as a perfect square is called completing the square. As you can see in Problems 8 and 9, completing the square can be used to solve quadratic equations that don’t appear to factor.
Use completing the square to solve the following equations. Find exact solutions.
$x^2 + 12x - 21 = 0$.
${x^2} + 2x - 4 = 0$
${x^2} - 4x + 1 = 0$
${x^2} - 20x - 100 = 0$
In Problem 10 the solutions you were finding are called the
roots of the equation since each equation is in the form
${\rm{BLAH}} = 0$. As you’ve seen before, these roots (these
solutions) can be interpreted as $x$-intercepts of a
corresponding quadratic function. For example, the roots of the
equation ${x^2} + 12x - 21 = 0$ are the
Find the exact zeros of the following quadratic functions.
$y = {x^2} + 6x - 1$
$y = x^2 - 10x + 4$
$y = x^2 - 2x - 15$
Find the exact coordinates of the vertex of each function presented in Problem 11 without using the graphing or table features of your calculator.
Use the information you have developed in Problems 11 and 12 to draw a graph of $y = {x^2} - 10x + 4$. Do not use the graphing or table features of your calculator. Label, on your graph, the exact coordinates of the vertex, the $x$-intercepts, and the $y$-intercept.
You should pat yourself on the back after completing Problem 13. You not only can fully analyze a linear function ($y = ax + b$): solve it, graph it, find its slope and intercepts without the calculator; you now have some ideas about how to fully analyze a quadratic function of the form $y = {x^2} + bx + c$. Later, we will get to analyzing the more general form $y = ax^2 + bx + c$, where $a$ can be any real number other than zero, and we will even look at what happens when there don’t appear to be any zeros (it turns out that there are zeros, but they are of a completely different nature).
Practice
What are the square roots of 400?
What are the square roots of 56?
Find the exact roots ${x^2} - 61 = 0$.
In each part below, determine what $c$ must be so that the resulting expression is a perfect square.
${x^2} + cx + 25$
${x^2} - cx + 1$
${x^2} + 24x + c$
$x^2 - 14x - 5 + c$
Find the exact solutions for each equation.
${x^2} + 18x - 100 = 0$
${x^2} - 4x - 1 = 0$
${x^2} = 14x - 20$
${x^2} + 6x + 8 = 0$
Find all the intercepts of each quadratic function.
$y = {x^2} - 2x - 9$
$y + 5 = {x^2} + 4x$
Find the exact coordinates of the vertex without using the graphing or table features of your calculator.
$y = {x^2} + 30x - 100$
$y = {x^2} - 18x + 80$
Without using the graph or table features of your calculator draw a graph of the equation. On the graph, label the exact coordinates of the vertex, the $x$-intercepts, and the $y$-intercept.
$y = {x^2} + 30x - 100$
$y = {x^2} - 6x + 6$
Problems
Find the exact solutions to $-x^2 = 40 - 22x$.
Find the exact solutions to ${x^2} + 5x - 4 = 0$.
Find the exact solutions to ${x^2} - 8x + 1 = 2x + 9$.
Find the exact solutions to ${x^2} + bx + c = 0$. The solutions here will not be explicit numbers, per se, but will have $b$’s and $c$’s in them.
The diagram below consists of an ${x^2}$- block and six $x$-blocks.

Use the diagram to figure out the right number to add to “complete the square” on the expression ${x^2} + 6x$. Then write the identity your diagram illustrates.
Make a similar diagram to show how to complete the square on the expression ${x^2} + 10x$.
Where precisely do the graphs of $y = {x^2} - 4x + 1$ and $y = 2x + 4$ intersect?
Where precisely do the graphs of $y = - {x^2}$ and $y = {x^2} - 4$ intersect?
Is there a number that has only one square root? No square roots?
If $x$ is a real number then what is the smallest value of ${x^2} + 8?$ What about ${x^2} + 8x + 8$?
There are two points $\left( {x,4} \right)$ that are 6 units from $\left( { - 2,7} \right)$. Find the exact values of $x$.
Let $y = {x^2} - 6x + 5$.
Rewrite the equation so that it’s in the form $y = {\left( {x - h} \right)^2} + k$.
Explain why $y = {\left( {x - h} \right)^2} + k$ is called the vertex form of the quadratic equation.
In a right triangle, the hypotenuse is 14 and one leg is 3 longer than the other. Find the lengths.
You take 3 consecutive numbers. You add the middle one to the product of the other two, and get 505. Find the three numbers.
A whiteboard is 8 feet wider than it is tall. It was damaged in a freak rainstorm and is missing a rectangle that is 3 feet by 2 feet in the lower right hand corner. The total area of useable whiteboard is 20 square feet.
To the nearest hundredth of a foot, find the dimensions of the whiteboard. What are these dimensions in inches?
Find the exact dimensions (in feet) of the whiteboard.
In the house below, the roof is an equilateral triangle of side length $x$ and the bottom part is a rectangle of dimensions $x$ by $y$. The total perimeter of the shape (outside edges only) is 100.
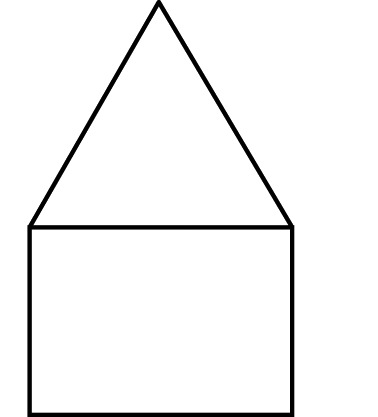
Write an equation for the perimeter
in terms of $x$ and $y$, and then write an equation for the
area in terms of $x$ and
Write the area in terms of $x$ alone.
Find the values of $x$ and $y$ that would make the area the largest.
You jump off a 9-meter diving board. At the same time, your friend jumps off a 10-meter diving board next to you. However, you and your friend have a different style of jumping. You jump up off the board with an initial speed of 1.6 meters/second. Your friend just steps off the board, without jumping at all. The functions describing your heights off the surface of the water in terms of time (in seconds) are
You: $a(t) = - 5{t^2} + 1.6t + 9$
Friend: $b(t) = - 5{t^2} + 10$
Who hits the water first?
When you jump in the air, do you ever get as high as the 10-meter board?
The line segment below is divided into two parts by point A. The ratio of its right part to its left part is the same as the ratio of the entire line segment to its right part. Note that the left part has a length of 1. Let $x$ stand for the length of its right part.

Write an equation saying the ratios are equal.
Determine the exact value of $x$.
Exploring in Depth
You’ve learned how to solve equations of the form ${x^2} + bx + c = 0$. In this problem you’ll tackle quadratic equations where the coefficient (the number in front) of ${x^2}$ is something other than 1. You might consider what you can do to each equation in order to turn it into an equation of the form ${x^2} + bx + c = 0$.
$2{x^2} + 8x - 12 = 0$
$3{x^2} - 12x = 21$
$- 4{x^2} + 8x - 5 = 0$
$- 2{x^2} + 10x - 8 = 0$
$\frac{2}{3}x^2 = x+1$
$ax^2 + bx + c = 0$, where $a \neq 0$.
(Continuation of Problem 25) Determine a formula for the $x$-coordinate of the vertex of the graph of $y = {x^2} + bx + c$.
(Continuation of Problem 39 Part f) Determine a formula for the $x$-coordinate of the vertex of the graph of $y = ax^2 + bx + c$, where $a \ne 0$.
Don’t use a calculator for this problem.
Evaluate ${1^2} - {( - 1)^3} + {0^4} - {1^5} + {( - 1)^6} - {0^7}$
Add $\frac{a}{b} + \frac{c}{d}$
Solve for $x$: $\frac{7}{x+2} = \frac{2}{x-3}$
16 hungry students come across 5 and a half leftover pizzas. If each pizza has 8 slices and the students split the pizzas evenly, how many slices does each student get?
Simplify $\dfrac{\frac12}{2}$, then simplify $\dfrac{1}{\frac{2}{2}}$.
Show that the graph of $y = - 3{x^2} + 12x - 1$ is a transformation of the graph of $y = {x^2}$.
There are some equations that are “quadratic in form,” meaning that they are not quadratic but they can be reduced to a quadratic equation. For example, ${x^4} - 2{x^2} - 8 = 0$ is such an equation if you let $y = {x^2}$ and then substitute into the equation, getting ${y^2} - 2y - 8 = 0$. Use this kind of thinking to solve the following equations.
${x^4} - 2{x^2} - 8 = 0$
${x^4} - 4{x^2} + 1 = 0$
${x^4} - 6{x^2} + 8 = 0$
$y^6 + 8y^3 = 20$
$y - 4\sqrt y - 12 = 0$
A ball is thrown from the top of a 65-feet tall building. The ball’s height above the ground is modeled by the equation $h = - 16{t^2} + 100t + 65$.
Sketch a reasonable graph of the height of the ball above the ground.
Determine the approximate time (accurate to the nearest tenth of a second) at which the ball is first 150 feet above the ground. Now find the exact time.
Use algebra to explain why the ball never reaches a height above the ground of 225 feet.
What is the maximum height of the ball?
For how long is the ball more than 150 feet above the ground?
Determine the exact time when the ball hits the ground.
To lay wall-to-wall carpeting in a living room and dining room takes 612 square feet of carpet. The living room floor is 3 feet longer than it is wide. The width of the dining room floor is 6 feet more than the width of the living room, and its length is twice the width of the living room. What are the dimensions of each room?
At one point we found the coordinates of the vertex of a parabola by finding the exact coordinate of the $x$-intercepts and then averaging these as a way of getting the $x$-coordinate of the vertex. What happens, however, if there are no $x$-intercepts? Let’s explore this issue by using the quadratic equation $y = {x^2} + 4x + 5$.
Use algebra to try to determine the exact coordinates of the $x$-intercepts. What happens? What does this mean in regards to finding the $x$-intercepts?
. Let’s suppose $\sqrt { - 1} $ exists (and so does $- \sqrt { - 1} $). Now, complete the algebra you started in Part a and use these zeros to find the exact $x$-coordinate of the vertex of the parabola. Check your work by inspecting the graph. Hmmm…
See if the kind of algebraic reasoning you used in Parts a and b will let you determine the coordinates of the vertex of $y = x^2 - 6x + 12$.