Looking at a large or complex problem can be fairly intimidating — where does one begin? It can seem that there is too much to take in all at once. Indeed, trying to understand the “whole” is often completely unhelpful at first, and we are better off just getting a handle on individual “parts” that make up the “whole”. To Take Things Apart is to break a problem down into smaller, more manageable “chunks” that we can understand. After we have solved the smaller problems, then we can use our results to rebuild the original problem and solve it.
You put a rubber band around a 3x5 “grid” of circles. Each circle has radius 1.
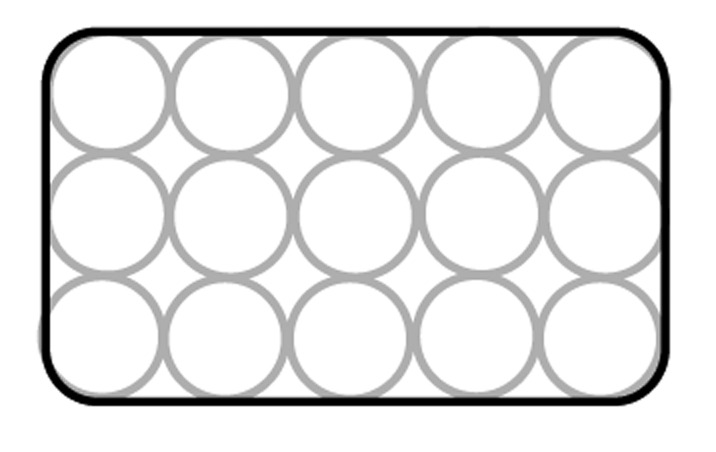
What is the length of the rubber band?
What percent of the area inside the rubber band is not contained in any circle?
We don’t have a name for the shape we’re trying to find the perimeter of in part a — it looks like a rectangle, but it has rounded corners. But we can still find the perimeter by breaking the shape up into pieces. For instance, we can start by finding the lengths of the parts of the sides that are straight — how long are they? It may help to draw some lines to section off this part of the shape for which you already have the perimeter. Now look at the part of the shape that’s left. Can you figure out how to get the remaining perimeter?
Now all that remains is to break the problem down into steps in order to figure out what to do. First let’s think about how to find a percentage of area. That’s going to be $\frac{{{\rm{The\: area\: inside\: the\: rubber\: band\: but\: not\: in\: the\: circles}}}}{{{\rm{The\: area\: inside\: the\: rubber\: band}}}}$. This fraction tells us that we need to break this problem into two parts: find the numerator and find the denominator. To get the denominator, we might be able to use a “take things apart” process similar to our method in part a. To get the numerator, you will also need to come up with a plan.
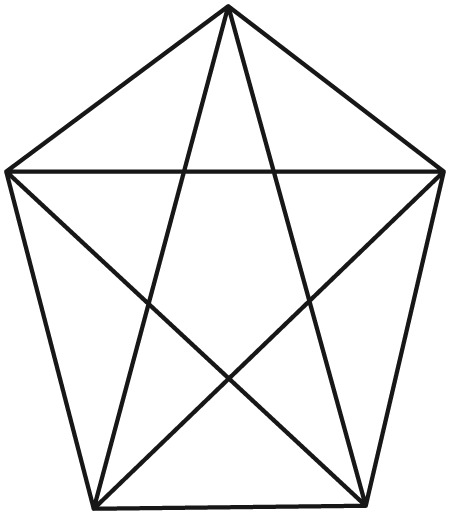
How many triangles are there whose three vertices are points on this 3 by 3 square grid? (Math Counts)

If you tackle this problem simply by drawing different triangles within the diagram, you might find yourself getting lost. In fact, all the overlapping triangles might lead you to think that you’ve found all of the triangles (when you probably haven’t), or you might just give up in the confusion of lines. So, one suggestion is to systematically take the diagram apart. First, look at the top-left square of points. How many triangles are there in this square? Now, how many of these squares exist in the 3 by 3 grid? So, how many triangles are there in the 3 by 3 grid that are of the form that fit into the top-left square?
Now let’s look for more triangles. Instead of using a square, expand your boundary shape to a 2x3 rectangle. Draw all the possible triangles that fit within the rectangle, excluding the ones you’ve already counted as part of a square. Now you can again multiply your answer by the number of rectangles that occur in the grid. Should you count overlapping rectangles or not?
Now, complete the problem by counting the rest of the triangles. While this problem takes some effort at solving, it certainly takes less effort if you take the diagram apart and build up the count in a step-by-step fashion. What’s more, counting systematically will increase your confidence that you’ve in fact found every triangle.
On the next page are some more “Take Things Apart” problems for you to enjoy.
A certain white six-sided die is 1 inch by 1 inch by 1 inch. Each black dot on the die is a circle with radius $.1$ inch. What’s the area of the white space on the entire die? (Remember that the area of a circle is $\pi {r^2}$.)
You put a coin on the top left square of a 3 by 3 checkerboard. You are allowed to make moves that go either one square to the right, or one square down. How many different ways can you get the piece to the bottom right? What if you are allowed to make moves either right, down, or diagonally down-right?
The diameter of the earth is about 7920 miles. Imagine that you stretch a string around the equator of the earth. If you add one foot to the string, then make the string hover around the earth like a ring around Saturn, what will be the distance between the string and the surface of the earth?
How many different three-letter “words” can be formed using the letters of the word “DEDUCT”?
How many different triangles are there in the figure below?
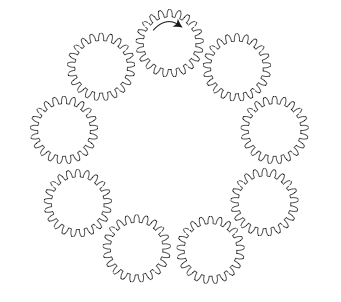
9 identical gears are arranged in a circle. One of the gears (call it “Gear 1”) is rotated clockwise. Which way will Gear 5 turn?
In the picture below, the big sphere is filled with air, and the two little spheres (which stack up to fit exactly inside the big sphere) are filled with water.
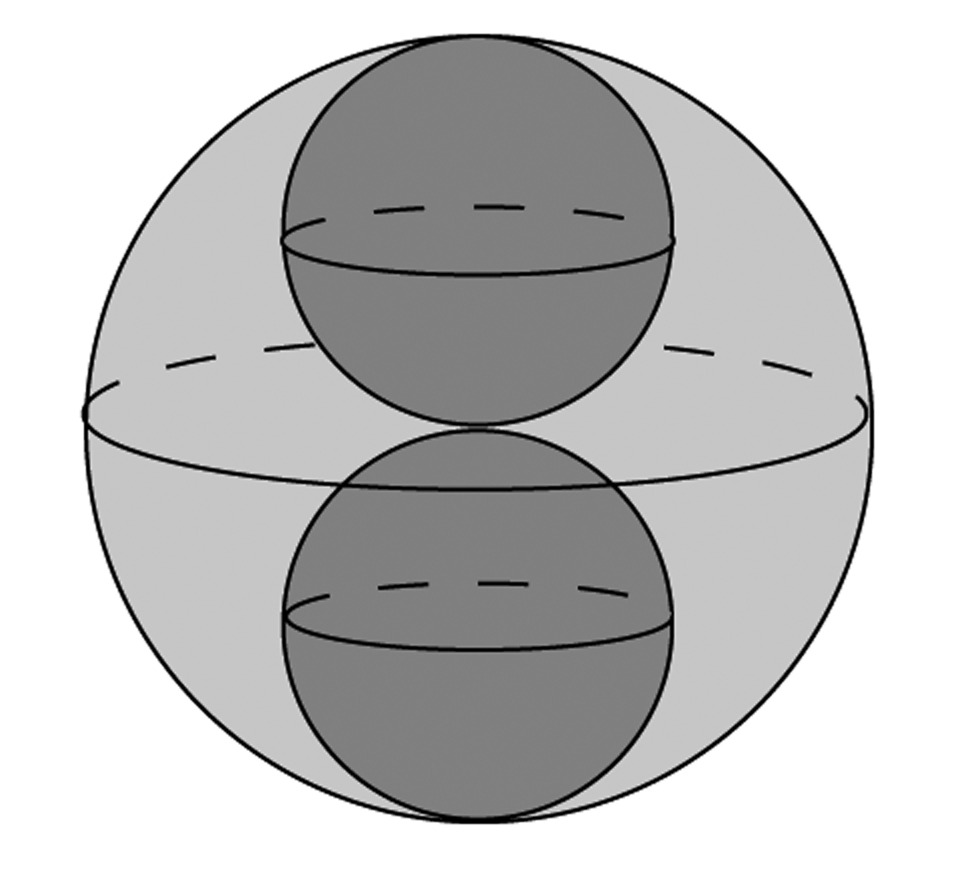
The radius of the big sphere is 12 inches. How much water is in the whole thing? How much air?
The average of 10 numbers is 53. The
average of 6 of these numbers is 57. What is the average of
the other 4?
(Copyright mathleague.com.)
The area of the “curved star” in the center of the diagram is $16 - 4\pi $. What is the area of the large square?
According to a story on NPR’s Marketplace, Starbucks sells about 1.9 billion cups of coffee a year. By manufacturing cups with 10% recycled materials, Starbucks’s supplier (the Mississippi River Corporation) is able to save 11,000 tons of wood per year. How much wood must it take to make one non-recycled coffee cup?
The base of a rectangular tank is three feet by two feet, and the tank is three feet tall. The water in the tank is currently just nine inches deep.
The water level will rise when a one-foot metal cube (denser than water) is placed on the bottom of the tank. By how much?
The water level will rise some more when a second one-foot metal cube is placed on the bottom of the tank, next to the first one. By how much?
(Copyright Phillips Exeter Academy.)
The Physicist Enrico Fermi was famous for asking students to estimate the answers to questions that, at first glance, seemed to be far too complicated to even approach. For example, to solve
How many pounds of trash do U.S. households throw out every year?
You might start with a quantity that is easier for you to reasonably estimate: the weight of the trash that your family throws out in a given week. (If it is your job to take the garbage out, you may be especially well-qualified to answer this question.) From there, you could reason from other well-known facts and reasonable guesses to scale up your answer to cover all U.S. households.
These next few problems can similarly be solved by breaking the problem down into pieces and coming up with your best estimate (which is not the same as just guessing).How many blades of grass are there on the Park soccer field?
How many cows are killed each day so that McDonald’s restaurants in the United States can serve up hamburgers?
If the Gym was filled to the brim with pennies, how much would it be worth?
A needle is what fraction of the size of a typical haystack?
How many piano tuners are there in the city of Chicago? (This was Fermi’s favorite problem.)
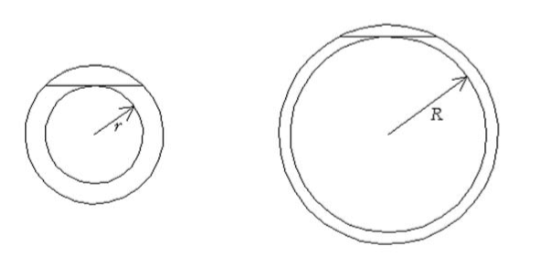
The line segment is tangent to the inner circle and is 100 m long in each diagram. Which ring has the larger area (i.e., area between the circles)?
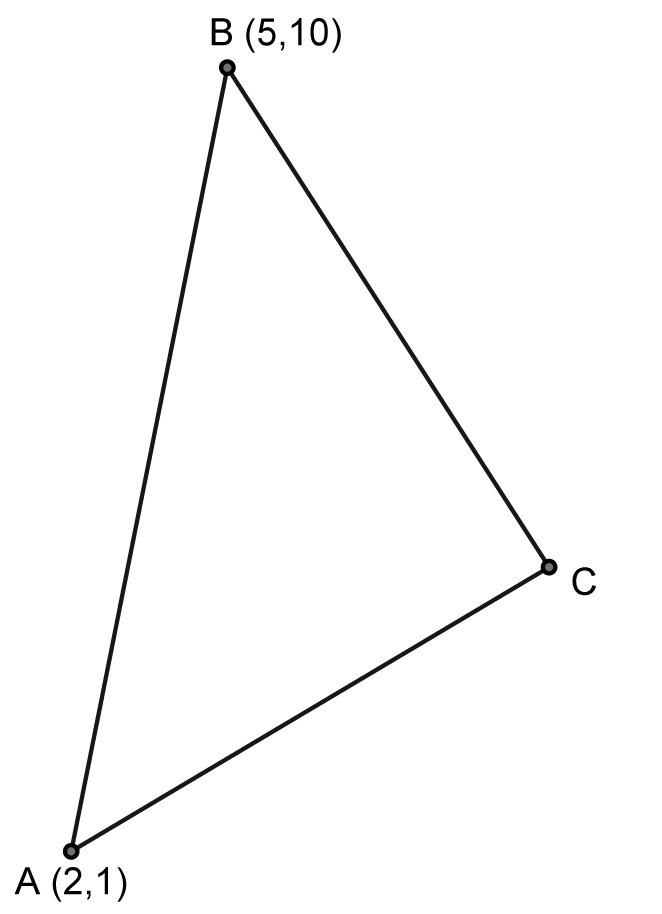
In the right triangle below, what is the product of the slopes of the 3 sides? (Assume that angle C is a right angle, and that AC is not horizontal)
Without looking up any formulas, find the surface area of a cylindrical can that has a diameter of 12 cm and a height of 12 cm.
A primitive earlier form of a pyramid was a ziggurat. A simple version could be constructed by making a square base consisting of, say, 9 cubes on a side. The next layer up is a square 7 cubes on a side, piled directly on top of the base and with the same center. This continues all the way up to the top single cube.
How many blocks in this ziggurat are hidden from view?
If the edge of each cube is 1ft long, what is the total edge length showing (2 overlapping edges only count as 1 edge)?
What would your answers to Parts a and b be if the base of the ziggurat was 99 cubes on a side?