Development
As you learned last year, factoring a number means expressing it as the product of two or more other numbers. For example, 40 can be factored as $2 \cdot 20$. Of course, 40 can be factored in many other ways as well.
What are all the ways that 40 can be factored into two whole numbers?
Since 20 can be factored as $4 \cdot 5$, 40 can also be factored into 3 numbers as $2 \cdot 4 \cdot 5$; and since 4 can also be factored into $2 \cdot 2$, 40 can be factored into 4 numbers as $2 \cdot 2 \cdot 2 \cdot 5$. You might also think of saying it could be factored into 5 or 6 numbers as $1 \cdot 2 \cdot 2 \cdot 2 \cdot 5$ or $1 \cdot 1 \cdot 2 \cdot 2 \cdot 2 \cdot 5$, but since those aren’t really different from $2 \cdot 2 \cdot 2 \cdot 5$, we will agree that 1 won’t “count” as a factor in the following problems, even though technically 1 is a factor of every number. Thus, at this point, 40 can’t be “broken down” any more than $2 \cdot 2 \cdot 2 \cdot 5$ (we are restricting ourselves to positive integers here, so we wouldn’t consider turning 5 into $2.5 \cdot 2$ or into $- 5 \cdot - 1$).
Find two different ways to factor 72 into two positive integers. For each of your answers, continue factoring them until they can’t be “broken down” any more. Finally, rearrange each of your final factorings so that the factors are in order from smallest to largest.
Factor 210 into the product of as many positive integers as possible. Compare your answer with a classmate’s. Based on this question and on question 2, what generalization might you now conjecture?
A number has been factored as much as possible when each of its individual factors cannot be broken down any more. Numbers greater than 1 that cannot be broken down any more (i.e., cannot be factored into smaller positive integers) are called primes. We say that the prime factorization of 40 is $2 \cdot 2 \cdot 2 \cdot 5$, or ${2^3} \cdot 5$ for short; we know it is a prime factorization because all of the factors (2, 2, 2, and 5) are primes. As suggested by questions 2 and 3, every positive integer greater than 1 has a unique prime factorization. As we will see, this uniqueness means that rewriting a number in its prime factored form will often be extremely useful, even though all we have done is written the same number in a different way.
Sometimes it can be tricky to know what the factors of a number are: that is, what divides into it evenly, leaving no remainder. For example, what numbers is 153 divisible by? It would clearly be helpful if one knew easy procedures (known as divisibility tests) that allowed one to see if smaller numbers divided arbitrary larger ones evenly. As a matter of fact, the divisibility tests for 2 and 5 are easy (what are they?), but it helps to know the tests for 3 and 11 as well (sadly, there is no easy test for 7).
If, when you add up the digits of a number, its sum is divisible by 3, then the number is divisible by 3 as well; on the other hand, if the sum is not divisible by 3, the number is not divisible by 3. So 14353 is not divisible by 3 (because $1 + 4 + 3 + 5 + 3 = 16$, which is not divisible by 3), while 55521 is. We will learn why the divisibility test for 3 is true later this chapter, but you might find it fun to ponder why it works on your own first!
Some of you may remember learning in 9th grade that a number is divisible by 11 only when the “alternating sum” is divisible by 11. So 4565 is divisible by 11 because is divisible by 11, as is 527494 because $+ 5 - 2 + 7 - 4 + 9 - 4 = 11$, but 6587 is not because $+ 6 - 5 + 8 - 7 = 2$ is not divisible by 11.
And now, a few problems to check your understanding of the above:
What is the largest number (other than 495 itself) that divides evenly into 495? Why do you know it’s the largest number that can do so?
Is 4806 prime? How about 4807? Quickly name 5 numbers between 4800 and 4900 that are divisible by 11.
Determine the prime factorization of 2310.
Is 91 prime? How could you be sure of your answer? What about 221? Or 223?
Come up with a procedure that can determine, with reasonable efficiency, whether a number is prime or not.
Determining in general if a positive integer is prime (i.e., has no factors other than itself and 1) turns out to be an increasingly difficult task the larger the number becomes. In fact, one of the most powerful ways of encrypting data on the internet — the so-called “RSA algorithm” — is based on the difficulty of finding the prime factorization of very large (over 100 digits!) integers.
Prime factorization also allows us to determine the answers to questions about the relationships between two (or more) numbers. Remember that it can be helpful to write the final prime factorization using powers; for example, the prime factorization of 484 is ${2^2} \cdot {11^2}$.
What is the largest number that divides evenly into both 216 and 270? This number is called the greatest common divisor of the two numbers and is written as gcd(180, 156). (For example, gcd(24, 36) = 12, as 12 is the largest integer that “goes into” both 24 and 36.)
If your answer to question 9 involved testing out a lot of different numbers, try writing out the prime factorization of each original number (i.e. 216 and 270) first and see if you can use them to be more efficient in finding their gcd.
Find gcd(168, 448) efficiently. How can you be sure you have found the largest possible number that “works”?
Find gcd(${2^{16}} \cdot {3^4}$, ${2^{13}} \cdot {3^8}$), or put another way, gcd(5308416, 53747712). Looking at the original prime factorizations of each number, what do you notice about the prime factorization of your answer?
Create a procedure that allows one to efficiently determine the gcd of two positive integers. Check it with 3 examples that you make up, where at least one of the examples is similar to problem 12 (i.e., where the two numbers are large but have simple prime factorizations).
Crucially, then, a prime factorization is important because all the factors of a number derive from the number’s prime factors. 24, for example, is ${2^3} \cdot 3$, and all of its factors — 2, 3, 4, 6, 8, 12, and 24 — are made up of combinations of the 2’s and 3’s found in the prime factorization.
In the following exercises, learn how powerful prime factorization is by solving them without your calculator!
How can you check to see if $32 \cdot 35$ equals $28 \cdot 40$ without determining either product?
Juniper says that when she multiplies $6 \cdot 24 \cdot 55$ it is equal to $21 \cdot x$, where $x$ is an integer. Explain if she is telling the truth or not.
Simplify $\frac{{64 \cdot 25 \cdot 14 \cdot 33}}{{28 \cdot 44 \cdot 15}}$ as much as possible.
What is the positive integer N for
which ${22^2} \times {55^2} = {10^2} \times {N^2}$?
Copyright www.mathleague.com.
Is ${6^4} \cdot {10^3}$ greater than, less than, or equal to ${8^2} \cdot {15^3} \cdot 6$?
The last few problems also are a reminder of the laws of exponents that you learned in middle school. Since ${5^6}$ is just $5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5$ and ${5^4}$ is just $5 \cdot 5 \cdot 5 \cdot 5$, it makes sense that
$\begin{array}{c} {5^6} \cdot {5^4} = (5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5) \cdot (5 \cdot 5 \cdot 5 \cdot 5)\\ = {5^{10}} \end{array}$
Similarly, because $\frac{{{5^6}}}{{{5^4}}}$ is just
$\frac{{5 \cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5}}{{5 \cdot 5
\cdot 5 \cdot 5}}$, it makes sense that some pairs of 5’s in
the numerator and denominator would “cancel” (because
$\frac{5}{5} = 1$) and thus
$\frac{{{5^6}}}{{{5^4}}} = \frac{5
\cdot 5 \cdot 5 \cdot 5 \cdot 5 \cdot 5}{5
\cdot 5 \cdot 5 \cdot 5}$
$= \frac{5
\cdot \cancel5 \cdot \cancel5 \cdot \cancel5 \cdot \cancel5 \cdot 5}{\cancel5
\cdot \cancel5 \cdot \cancel5 \cdot \cancel5}$
$= 5^2.$
Lastly, ${({5^4})^3}$ is just $(5 \cdot 5 \cdot 5 \cdot 5)(5 \cdot 5 \cdot 5 \cdot 5)(5 \cdot 5 \cdot 5 \cdot 5)$, so ${({5^4})^3} = {5^{12}}$.
By using the reasoning of the previous paragraph, finish
the following equations, where $x$ is the base, and $a$ and $b$ are
exponents:
${x^a} \cdot {x^b} = \hspace{3em} $ $\frac{x^a}{x^b} = \hspace{3em} $ ${({x^a})^b} = $
For the second law in question 15, what are you assuming about $a$ and $b$? Try different values of $a$ and $b$ to clarify your answer.
Simplify the following:
${x^{13}} \cdot {x^7}$
$\frac{3^{28}}{3^{24}}$
${\left( {{x^5}} \right)^6}$
$(\frac{x^8 \cdot x^9}{x^6})^2$
What do you think ${3^0}$ should be equal to? Why? Come up with a specific argument to defend your view (and don’t use your calculator!).
Let’s explore the expression a bit more.
If ${3^4} = \frac{{{3^p}}}{{{3^q}}}$, then what are possible pairs of values for $p$ and $q$? Give at least 3 pairs.
Using similar reasoning as in part a, what would it appear ${3^0}$ should be equal to? What about ${497^0}$?
Which answer do you trust more, your answer to question 18, or your answer to part b above? Explain.
Finally, make a chart of the powers of 3, starting at ${3^5}$ and going down to ${3^1}$. Looking at this chart, what do you think $3^0$ should be?
Based on part d and your own conclusions, can you revise your answer a little to question 16?
What do you think ${6^{ - 3}}$ should be equal to? Is your answer the same as $- ({6^3})$? Again, come up with a specific argument to justify your answer.
Let’s look a bit deeper into the idea of negative powers.
Using similar reasoning as in question 19a, what would it appear ${6^{ - 3}}$ should be equal to? (Write your answer as a reduced fraction.) Does your answer equal what you thought in question 20?
Make a chart of the powers of 6, starting at ${6^5}$ and going down to ${6^0}$. Following this idea, what do you think ${6^{ - 1}}$ would be? How about ${6^{ - 2}}$ and ${6^{ - 3}}$? Again, write your answers as fractions, rather than using decimals.
Based on parts a and b and your own conclusions, can you revise your answer to question 16 even more than you did in question 19e?
What should ${x^6}$ be multiplied by to equal ${x^2}$? What should ${x^6}$ be divided by to equal ${x^2}$? Test that your answers work with a specific value of $x$, and then explain how the answers are related to each other.
Rewrite $\frac{x^{-4}}{x^7}$, $\frac{{{3^{ - 5}}}}{{{3^6}}}$, $\frac{x^8}{x^{-5}}$ $\frac{{{2^{ - 8}}}}{{{2^{ - 3}}}}$, $\frac{{{x^{ - 6}}}}{{{x^{ - 4}}}}$ and $\frac{{{x^{ - 7}}}}{{{x^{ - 11}}}}$ so that your final expressions have only positive exponents.
Simplify $\frac{{{x^8}{x^5}}}{{{x^3}{x^7}}} \;$, $\big(\frac{{{x^8}{x^5}}}{{{x^3}{x^7}}}\big)^4$, and $\big(\frac{{{x^8}{x^5}}}{{{x^3}{x^7}}}\big)^{-4}$. Then write each of your “simplified” answers with only positive exponents, if they aren’t already.
Practice
Without using a calculator, find all the prime factors of 99792 that you can. Then, using a calculator, find the complete prime factorization of 99792.
Find gcd(1240, 4400). If you wish, you can express your answer not as a number, but as the prime factorization of that number.
Determine if $\frac{{60480}}{{2268}}$ is an integer without using a calculator!
What values of $x$ and $y$ satisfy $36 \times {5^x} = 225
\times {4^y}$?
Copyright www.mathleague.com.
Arrange from biggest to smallest: ${3^{ - 3}}$, ${( - 3)^3}$, ${2^{ - 2}}$, ${( - 2)^2}$, ${( - 3)^{ - 3}}$, ${( - 2)^{ - 2}}$.
Simplify $\frac{{{2^7} \cdot {2^5}}}{{{2^4} \cdot {2^6}}}$, $\big(\frac{{{2^7} \cdot {2^5}}}{{{2^4} \cdot {2^6}}}\big)^3$, and $\big(\frac{{{2^7} \cdot {2^5}}}{{{2^4} \cdot {2^6}}}\big)^{-4}$ so that each answer is extremely simple: 2 raised to an integer power. Don’t use a calculator.
Can ${3^4} \cdot {2^5}$ be written in the simpler form ${a^b}$ (where $a$ and $b$ are integers and $b \ne 1$)? If yes, check your answer by trying it out with specific numbers $a$ and $b$ just to be sure.
Going Further
Do the laws of exponents continue to hold when dealing with two variables? Let’s check this out.
Does ${\left( {xy} \right)^5} = {x^5}{y^5}$? Try testing this “rule” with specific numbers, and, if it seems to work, see if you can prove the rule using algebra.
Generalizing from part a, what would ${\left( {xy} \right)^a}$ be equal to?
Using similar reasoning, how could one rewrite $\big( \frac{x}{y} \big)^a$?
What would ${\left( {xy} \right)^8}{\left( {xy} \right)^4}$ equal? How about ${\left( {xy} \right)^3}{\left( {xy} \right)^{ - 7}}$?
Following the pattern in part d, how could you rewrite ${\left( {xy} \right)^a}{\left( {xy} \right)^b}$?
Can you rewrite $\frac{{{{\left( {xy} \right)}^a}}}{{{{\left( {xy} \right)}^b}}}$ as well?
How about ${\left( {x + y} \right)^a}$— does it simplify easily? How can you check your answer?
Now let’s apply what we’ve learned in question 32.
Can $\frac{{{x^5}{y^7}}}{{{y^3}{x^2}}}$ be simplified? How about $\big(\frac{{{x^5}{y^7}}}{{{y^3}{x^2}}}\big)^3$? Finally, howzabout $\big(\frac{{{x^5}{y^7}}}{{{y^3}{x^2}}}\big)^{-6}$?
Simplify $\frac{{{2^3} \cdot
{3^4}}}{{{2^5} \cdot 3}}$ and $\big(\frac{{{2^3} \cdot
{3^4}}}{{{2^5} \cdot 3}}\big)^{-2}$so that your answers are in the
form
Simplify $\big(\frac{4x^{-3}y^7}{x^8y^3}\big)^{-2}$ and $\big(\frac{x^8y^3}{4x^{-3}y^7}\big)^2$. Are you surprised by the two answers?
Rewrite $\big(\frac{kx^ay^b}{x^cy^d}\big)^e$ so that your answer is in the form
${k^P}{x^Q}{y^R}$, where
Here are a couple more doozies based on what you learned in question 33. Don’t use a calculator!
What simple number is equivalent to ${\left( {{3^2} \cdot {7^4}} \right)^4}{\left( {{5^8} \cdot {7^{ - 5}}} \right)^3}{\left( {3 \cdot {5^4}} \right)^{ - 6}}$?
What is $\big(\frac{16g^6}{9^6t^{-5}}\big)^{-2} \cdot \big(\frac{3^6 t^{-3}}{2^2 g^3}\big)^4 $, simplified?
You know from the laws of exponents that $x^2x^5 = x^7$, or that ${x^a}{x^b} = {x^{a + b}}$. We can use this identity to help us think of square roots in a different way — as an exponent.
What does $(\sqrt x )(\sqrt x )$ equal?
So if $\sqrt x = {x^N}$, what must $N$ be?
If $p \cdot p \cdot p = x$, what
must $p$ equal, in terms of $x$? Put
another way, if we say that $p = {x^N}$, what does $N$
equal?
(This number is called a “cube root” of $x$, i.e., since $2
\cdot 2 \cdot 2 = 8$, 2 is a cube root of 8. This can also
be written as $2 = \sqrt[3]{8}$, where the $\sqrt[\uproot{8}\leftroot{-1}3]{\quad}$ symbol indicates “cube root”.)
If ${p^5} = x$, what would $p$ equal in terms of $x$? That is, if we say that $p = {x^N}$, what does $N$ equal?
If $p = \big(\frac{1}{32}\big)^{(\frac{1}{5})}$, what would $p$ be? If $q = \sqrt[5]{{\frac{1}{{32}}}} \;$, what is $q$ ?
In general, then, if $\sqrt[n]{x} = {x^N}$, how are $N$ and $n$ related? Give a specific example or two to clarify.
Using what you learned in question 35, simplify each expression as far as possible. No calculator necessary, although feel free to check!
$\left( {{{16}^{\frac{1}{2}}}} \right) + \left( {{{16}^{\frac{1}{4}}}} \right)$
${64^0} + {64^{\frac{1}{3}}} + {64^{\frac{1}{2}}} + {64^1}$
$\left( {\sqrt[3]{{241}}} \right)\left( {{{241}^{\frac{1}{3}}}} \right)\left( {\sqrt[3]{{241}}} \right)$
$\big(81^{\frac{1}{4}}\big)^{-2}$
${125^{\frac{1}{3}}} \cdot {36^{ - \frac{1}{2}}}$
You now know how to calculate ${64^0},\;{64^{\frac{1}{3}}},\;{64^{\frac{1}{2}}},\;{64^1}$ and ${64^2}$. Let’s broaden our horizons even more!
Suppose a friend told you that he had just figured out how to calculate ${64^{1.5}}$. Based on what you already know about powers of 64, about how big a number do you think this is? Explain.
${64^{1.5}}$ can also be written as ${64^N}$, where $N$ is a simple fraction. What is $N?$
Now further rewrite ${64^N}$ by using the property of exponents that tells us we can rewrite ${x^{12}}$ as ${\left( {{x^3}} \right)^4}$.
Using your result from part c, you should now be able to compute a precise answer to ${64^{\frac{3}{2}}}\;( = {64^{1.5}})$. What is it, and does it agree with your answer in part a?
Similarly, what would ${64^{\frac{2}{3}}}\;( = 64\overline {^{.666}} )$ equal? How about ${4^{2.5}}$?
Finally, what is ${7^{1.3}}$? Explain what it means to raise a number to the 1.3 power. Once you’ve done that, do the same for ${7^{1.29}}$.
One can also solve equations quite easily when they contain powers. For example, ${x^3} = 11$ can be solved by taking advantage of the laws of exponents and raising each side to the 1/3 power: ${\left( {{x^3}} \right)^{\frac{1}{3}}} = {11^{\frac{1}{3}}}$, the idea being that because the exponents on the left side multiply, the exponent becomes “1”, and so it simplifies to $x = {11^{\frac{1}{3}}}$ (or $\sqrt[3]{{11}}$). Solve the following equations for $x$, keeping in mind the strategies in the paragraph above:
${x^5} = 32$
${x^{\frac{1}{5}}} = 32$
$3{x^3} = 81$
$\frac{16}{64} \; x^5=8$
${x^{\frac{2}{3}}} = 9$
${x^{2.71}} = 126$
$5x^{3.87}=1000$
Practice (No Calculators!!)
Simplify ${\left( {{x^{ - 17}}{x^8}} \right)^{ - 3}}$ in two different ways:
By simplifying inside the parentheses first, and then applying the outside exponent.
By applying the outside exponent first, and then simplifying.
Confirm that your answers in parts a and b are the same.
Simplify $\big(\frac{p^9q^{-5}}{q^7p^4}\big)^3$ and $\big(\frac{p^9q^{-5}}{q^7p^4}\big)^{-3}$. What do you notice?
Does $\big(\frac{w^6t^7}{t^{-8}}\big)^4$ equal $\big(\frac{w^3t^{20}}{w^{-5}}\big)^3$? Explain.
Don’t use a calculator for this problem.
Divide $\frac{{10}}{3} \div \frac{5}{2} \:$.
Factor $4x^3 – 12x^2$.
Factor $x^2 – 25$.
Solve for $x$: $x(x+3) – 1= \; –3$.
Solve for $x$, looking up the quadratic formula if necessary: $x^2 – 4x – 6=0.$
What is $\frac{(m^{-4}n^{12})^{-5}}{(n^{-6}m^3)}$ simplified?
Simplify $\big(\frac{12x^{-2}y^5}{8x^{-6}y^9}\big)^3$ .
The volume of a cube is 2197 cm$^3$. Find the total surface area of the cube. (Calculators allowed.)
Write ${5^5} \cdot {5^8} \cdot {8^5} \cdot {8^8}$ in the form $a^b$.
What is $\sqrt {{{17}^2}}$? What is $\sqrt[3]{{{5^3}}}$?
Which is bigger: $\sqrt[3]{37^2}$or $(\sqrt[3]{37})^2$? Why?
What does $8^{(\frac{4}{3} \;)} \cdot 4^{(\frac{3}{2} \;)}$ equal?
Simplify $\sqrt[3]{\sqrt[4]{x^{24}}}$.
Write ${25^4} \cdot {125^{ - 2}}$ as a power of 5.
Solve $2r^4=162$.
Problems (Still No Calculators!)
How many prime numbers under 10000 have digits that add up to 9?
If the sum of two prime numbers is 999, what is their
product?
Copyright www.mathleague.com.
Explain why the product of any three consecutive integers has to be divisible by 6.
The dimensions of a rectangular box (in cm) are all positive integers, and the volume of the box is 2002 cm$^3$. What is the least possible sum of the three dimensions?
(Calculators allowed.) What is the smallest positive
integer that is NOT a factor of $1 \times 2 \times 3 \times 4
\times 5 \times 6 \times ... \times 18 \times 19 \times 20?$
Copyright www.mathleague.com.
Does ${6^6} + {6^6} + {6^6} + {6^6} + {6^6} + {6^6}$ equal
${36^6}$? ${6^{36}}$? ${6^7}$? ${36^{36}}$? Or something
else in the form ${a^b}$? Explain.
(Appeared on AMC-12 competition, 1992)
Express $\frac{{{2^1} + {2^0} + {2^{ - 1}}}}{{{2^{ - 2}} + {2^{ - 3}} + {2^{ - 4}}}}$ as a single, simple fraction. (Appeared on AMC-12 competition, 1987)
When 270 is divided by the odd number X, the answer is a
prime number. What is X?
Copyright www.mathleague.com.
What is the simplest expression for
$\frac{{{2^{40}}}}{{{4^{20}}}}$?
Copyright www.mathleague.com.
What is the simplified value of
$\frac{{{{4444}^4}}}{{{{2222}^4}}}$?
Copyright www.mathleague.com.
If you double $x$, by what factor does the expression $\frac{{{x^7}{x^{ - 2}}}}{{{x^3}}}$ grow?
A composite number is a whole number that is greater than 1 and not prime — that is, it has factors other than itself and 1.
What is the smallest composite number that is not divisible by 2 or 3?
What is the smallest composite number that is not divisible by 2, 3, or 4?
What is the smallest composite number that is not divisible by 2, 3, 4, or 5?
(Calculators allowed.) Now determine the smallest composite number that is not divisible by 2, 3, 4, 5, 6, 7, or any of the numbers up to and including 100.
Order these, from smallest to largest, without using a calculator: ${1000^{\frac{1}{{1000}}}}$, $\big(\frac{1}{1000}\big)^{1000}$ , ${1000^{ - 1000}}$, $\big(\frac{1}{1000}\big)^{\frac{1}{1000}}$, $\big(\frac{1}{1000}\big)^{-1000}$
You are going to randomly choose three integers (repetition allowed) from 0 to 5, and call them $k$, $m$, and $n$. What’s the probability that ${2^k}{3^m}{5^n}$ is NOT divisible by 5?
What is the only number $x$ which satisfies $\sqrt {1992} =
1992\sqrt x $?
Copyright www.mathleague.com.
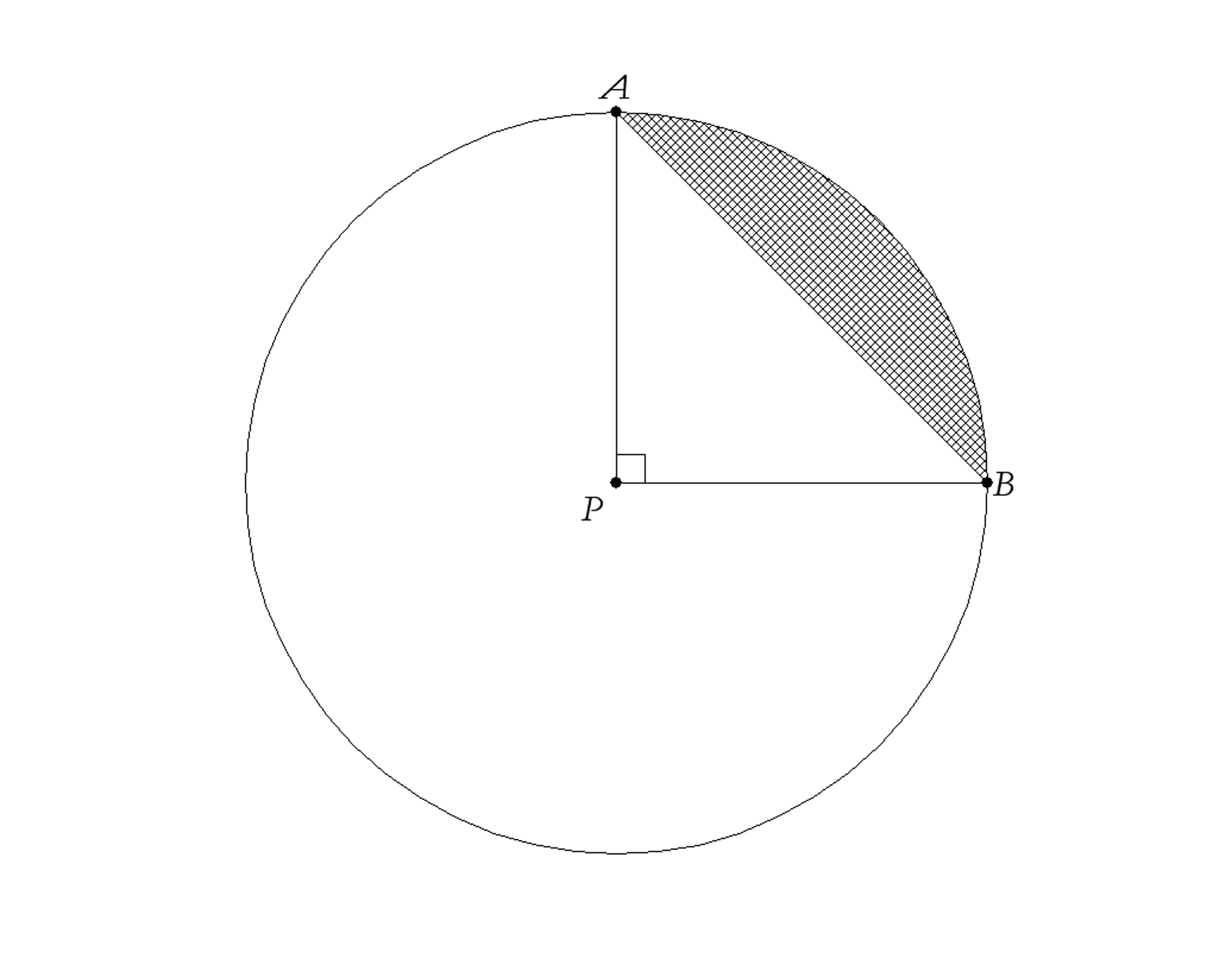
In circle P, the length of $\overline {AB} $ is $\sqrt {50} $. Find the area of the shaded region.
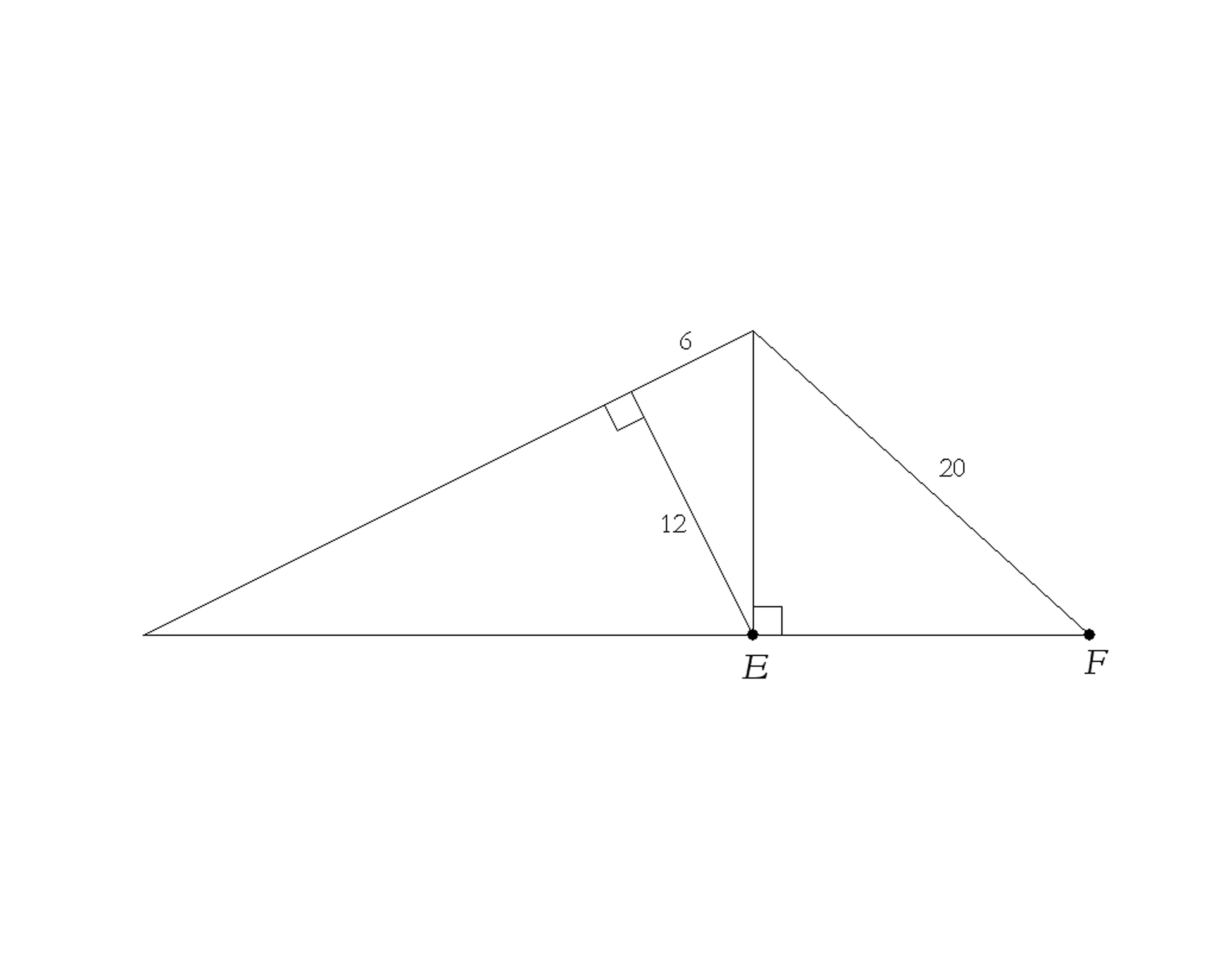
Find EF exactly.
Triangle ABC has a right angle at C. If sin B $= \frac{2}{3}$ what is tan B, expressed as a fraction?
Why must $\sqrt {17} $ be a non-terminating decimal? Put another way, why can’t a terminating decimal multiplied by itself = 17?
What is the positive number $x$ for which $x = \sqrt[3]y$ and $\sqrt y = 8$?
Copyright www.mathleague.com.
If ${x^{64}} = 64$, what is the exact value of ${x^{32}}$?
Copyright www.mathleague.com.
In simplest form, what is the numerical value of $\sqrt
{1985} \,\,\sqrt[3]{{1985}}\,\,\sqrt[6]{{1985}}$?
Copyright www.mathleague.com.
Which kind of number does not appear to have a 10th root? Which kind of number has an integer as its 10th root?
If $\sqrt[5]{x} = 4$ , what is the value of $\sqrt x $?
Copyright www.mathleague.com.
What does $\sqrt 7 \sqrt 3 \sqrt 2 \sqrt 5 \sqrt {10} \sqrt {21} $ equal? Think before calculating!!
Rewrite $\big(\frac{1}{4}\big)^{-\frac{1}{4}}$ as the root (i.e. square root, cube root, and so on—you choose !) of an integer that is NOT 4.
What is the value of $x$ which satisfies $\sqrt[3]{{x\sqrt x
}} = 4$?
Copyright www.mathleague.com.
If $x \ge 0$, then $\sqrt {x\sqrt {x\sqrt x } } $ is equivalent to ${x^N}$. What is $N$?
The function $s$ takes a number and outputs the sum of its “proper” divisors, meaning that 1 is considered to be a divisor but the number itself is not.
Find $s(8)$.
A perfect number is a number $n$ for which $s(n)=n$. How many perfect numbers are between 2 and 10?
An abundant number is a number n for which $s(n)>n$. Find the first abundant number.
A pair of numbers is said to be amicable when the proper divisors of each number add up to the other number.
Verify that 220 and 284 are an amicable pair.
Write the definition of amicable numbers using the $s(n)$ notation.
Exploring in Depth (No Calculators Still!)
Which is bigger, ${2^{3000}}$ or ${3^{2000}}$? Prove your
answer.
Copyright www.mathleague.com.
Write $\frac{{{{15}^{30}}}}{{{{45}^{15}}}}$ in the form
${a^b}$, if possible.
If it is not possible, explain why not.
(Appeared on AMC-12 competition, 1993)
If ${3^x} = 5$, what is the value of ${3^{\left( {2x + 3}
\right)}}$?
Copyright www.mathleague.com.
What is the integer $n$ for which ${5^n} + {5^n} + {5^n} +
{5^n} + {5^n} = {5^{25}}$?
Copyright www.mathleague.com.
Take any 6-digit number that repeats 3 digits twice in the same order, like 596596$. It will always be divisible by 7, 11, and 13. Why? (Calculators allowed.)
How many distinct pairs of positive
integers $\left( {m,n} \right)$ satisfy ${m^n} = {2^{20}}$?
Copyright www.mathleague.com.
How many positive integers less than 50 have an odd number
of positive integer divisors?
(Appeared on AHSME 41 competition)
If $x > y > 0$, then express
$\frac{{{x^y}{y^x}}}{{{y^y}{x^x}}}$ using only a single
exponent.
(Appeared on AMC-12 competition, 1992)
Earlier, you learned how to calculate a number such as ${8^{\frac{2}{3}}}$.
In fact, there are two different plausible ways of evaluating a number like ${8^{\frac{2}{3}}}$: as $\big(8^\frac{1}{3}\big)^2$ or as ${\left( {{8^2}} \right)^{\frac{1}{3}}}$. Are these two numbers in fact equal? Explain why or why not.
Try calculating both ${27^{\frac{4}{3}}}$ and ${32^{\frac{6}{5}}}$ in each of the ways described in part a. Which is easier, and why?
Multiplying and dividing numbers and/or expressions that have roots and/or exponents in them becomes considerably easier if all the roots are converted to exponents. Also often helpful in harder problems is to try to give all the exponents the same base. For example, the easiest way to simplify ${2^5} \cdot {8^4}$ is to think of “8” as “${2^3}$”:
Simplify the following:
${4^3} \cdot {64^5}$
${2^{ - 4}} \cdot {32^2}$
$\frac{{{3^5} \cdot {{18}^4}}}{{16}}$
${7^{\frac{5}{6}}} \cdot {49^3}$
$\frac{{{{81}^{\frac{3}{8}}}}}{{{{27}^{\frac{1}{2}}}}}$
(Calculators allowed.) In addition to the greatest common divisor, another interesting numerical concept is called the least common multiple.
What is the smallest positive integer that is a multiple of 30 and also a multiple of 42? This number is called the “least common multiple” and is written as lcm(30, 42). (For example, lcm(6, 8) = 24, as 24 is the smallest number that is both a multiple of 6 and a multiple of 8.)
If your answer to part a involved testing a large amount of numbers, try using the prime factorizations of the numbers to help you see how to find the lcm efficiently.
Find lcm(84, 126) efficiently. How can you be sure you have found the smallest possible number that works?
Find lcm(${2^{16}} \cdot {3^4}$, ${2^{13}} \cdot {3^8}$). Looking at the original prime factorizations of each number, what do you notice about the prime factorization of your answer?
Create a procedure that allows one to efficiently determine the lcm of two numbers. Once again, check with 3 examples you devise, with at least one of the examples similar to part d.
Take any two positive integers $x$ and $y$. (Calculators allowed.)
Find their gcd and lcm.
Multiply the gcd and lcm together.
Now multiply the original numbers $x$ and $y$ together. What do you notice?
Try parts a through c with 5 different pairs of positive integers $x$ and $y$.
What is going on here? Explain carefully in terms of the prime factorizations of $x$ and $y$. (Hint: Go back to questions 13 and 92e and look at how you were able to find the gcd and the lcm efficiently, and compare.)
Sometime around 5th grade, you were taught to add fractions $\frac{a}{b}$ and $\frac{c}{d} \;$ by finding a common denominator. Assume $b$ and $d$ are positive.
Explain whether you should be finding the gcd or the lcm of $b$ and $d$ if you want to find their smallest possible common denominator.
By the way, why do you need a “common” denominator to add fractions anyway? Why not just add them using different denominators?
If $x = \sqrt {2000} $ and $y = \sqrt {2001} $, what is
the simplified numerical value of ${(x + y)^2} + {(x - y)^2}$?
Copyright www.mathleague.com.
What on earth could ${4^{\sqrt 2 }}$ mean? Could you determine approximately how big it would have to be?
Let’s learn about how simplest radical form directly relates to prime factorization. (Calculators allowed.)
Put $\sqrt {99} $ and $\sqrt {884} $ into simplest radical form.
Explain, for an arbitrary integer $n$, how you would go about putting $\sqrt n $ into simplest radical form.
Now try simplifying $\sqrt {907} $. What makes you confident that you are definitely in simplest radical form?
Explain why you don’t have to test any numbers above 31 when checking to see if 907 is prime.
Now try simplifying $\sqrt {529} $, $\sqrt {551} $, and $\sqrt {557} $.
Given what you learned in parts c through e, can your answer in part b be improved or clarified? Are you confident your method will efficiently put $\sqrt n $ into simplest radical form? Explain.
Try your method on $\sqrt {343} $, $\sqrt {379} $, $\sqrt {403} $, $\sqrt {765} $, $\sqrt {1517} $, $\sqrt {1373} $, and $\sqrt {1763} $.
Let’s take a look at a proof the Greek mathematician Euclid came up with over 2000 years ago to show that there are an infinite number of primes. Euclid did this by assuming that there were a finite number of primes, and then showed that assuming that is the case turns out to be self-contradictory. Follow along to see his “moves”!
If there were a finite number of primes, we could call the largest one $“P”$. Euclid then asked us to consider $“Q”$, the number that has a prime factorization that includes each of the primes exactly once. Explain clearly how one could calculate $“Q”$.
Euclid then made his biggest “move”. Remembering that all the primes divide evenly into $“Q”$, Euclid asks us to consider the number $Q + 1$. Which of the primes do you think would go evenly into $Q + 1$ as well? Why?
What can you conclude about $Q + 1$, now that you have established that it has no prime factors?
Why does your conclusion contradict what you assumed at the start of the problem?