And Now For Something Completely Different— A Mindreading Textbook!
Don’t believe it? Try this!
Pick a number, any number.
Add 4 to it.
Square your new number.
Subtract 16 from your answer.
Divide what you have by the original number you picked.
Finally, subtract the original number.
This textbook knows what you got as your answer for Part e, and in fact it predicted ahead of time what you were going to get. Oh, you don’t believe it? Check out Part g.
Why should I tell you? You think I’m a liar. Oh, alright, I’ll tell you, but only if you promise to be impressed. See part h for enlightenment.
I’ll tell you, not that you deserve it. Your answer to Part e is…(drum roll please)…eight. Now then, kiddo, never doubt a talking textbook again.
Development
You may have seen a trick like the one above before and wondered how it worked. Let’s look at a few of them and see if we can figure out how they “tick”.
Have a friend pick a number without telling it to you, and then, keeping their calculations to themselves, ask your friend to:
Add 8 to it.
Now multiply by 3.
Subtract 11.
Multiply by 2.
Add 4.
Finally, have them divide by 6 and tell you the answer.
From their answer to Part f, you can now figure out their original number and impress the socks off of them. How? Try out your solution with a classmate and see if it works.
Let’s figure out what happened in Problem 2 by using algebra. Let’s call the original number your friend was thinking of “$x$”.
What number would they have after adding 8 to their original number?
And after multiplying by 3? Remember to use parentheses!
How about after subtracting 11? Simplify your answer.
After multiplying by 2 and adding 4 and simplifying, what expression do you have?
Now divide your answer in Part d by 6, and simplify your answer again. Remember that with fractions, $\frac{{a + b}}{c} = \frac{a}{c} + \frac{b}{c}.$
So, given your answer in Part e, how can you determine your friend’s original number?
Here’s a trickier one. Think of the age of anyone you know.
Multiply it by 10.
Add 1.
Multiply by 2.
Add 21.
Multiply by 5.
Your answer to Part e will end in the two digits “15”. Remove those last two digits to get a new number.
Subtract 1 from the new number, and that is the age you were thinking of. Why? (Hint if you’re having trouble: What you did in Part f can also be thought of as a subtraction followed by a division—how so?)
Here’s a more difficult variation. Pick a positive number.
Three less than that number, multiplied by two more than that number is…
Now take your answer from Part a and add the original number.
Add 6 more.
Take the square root. Ta da! Why does this work?
Figuring out Problem 5 required that you understand how to multiply two expressions together like $\left( {x - 3} \right)\left( {x + 2} \right)$—you use the distributive law and then combine “like” terms. Here, then, we get
${x^2} + 2x - 3x - 6 = {x^2} - x - 6$.
Recall that like terms are those that have the same power of $x$.
Take two 2-digit numbers, Betty and Crocker.
Divide Betty by Crocker. (i.e. $\frac{{{\rm{Betty}}}}{{{\rm{Crocker}}}}$)
Raise your answer to the 4th power, and then square the result. Call this “Vanilla”.
Now, instead, divide Crocker by Betty.
Cube what you got, and then cube it again. Call this “Chocolate”.
Multiply “Vanilla” times “Chocolate”.
Multiply your answer in Part e by Betty. What do you get?
Instead, divide your answer in Part e by Crocker, and then take the reciprocal. Now what do you get?
Explain the mystery of the universe’s existence, or at least Parts f and g.
Let’s go back to Problem 1, the introductory problem.
Calling the original number $x$, represent what “happens” to the number algebraically in each step.
To understand why the trick works, we have to simplify the complicated expression obtained in Part a. The first two steps produces ${\left( {x + 4} \right)^2}$; how can this expression be simplified? Check with an individual value of x to see if your simplification is plausible. Remember, ${\left( {x + 4} \right)^2} = \left( {x + 4} \right)\left( {x + 4} \right)$.
After the 3rd and 4th steps, you should have $\frac{{\left( {{x^2} + 8x} \right)}}{x}$. This can be simplified by factoring the numerator. Do so.
Just as $\frac{{6 \cdot 13}}{6}$ can be simplified by realizing that $\frac{6}{6} = 1$ and that we can thus cancel out the 6’s, leaving just 13, the same is true with $x$’s and $y$’s. For example, $\frac{{y\left( {x - 5} \right)}}{y}$ is just $x - 5$, and $\frac{{{w^5}(x + w)}}{{{w^5}(x + 7)}}$ is just $\frac{{(x + w)}}{{(x + 7)}}$. Now further simplify your answer to Part c.
After the next and final step, you should now understand the “trick”! To check your understanding, construct a similar problem where the first two steps are to subtract 5 from the number and then squaring the result, and the final step yields the original number. (No square rooting allowed!!)
Even when you are dealing with two or more variables, the following basic principles still hold and can be quite handy:
Combining like terms when adding or subtracting (meaning terms that have the same powers of the same variables)—
- \begin{split}2xy - 5xy = - 3xy\end{split}
- \begin{split}7{w^2}{v^4} - 5{w^2}{v^4} = 2{w^2}{v^4}\end{split}
Distributing—
- \begin{split}3xy\left( {2xy - 5x{y^2} + 4{x^2}y} \right) = 6{x^2}{y^2} - 15{x^2}{y^3} + 12{x^3}{y^2}\end{split}
- \begin{split} \left( {7x + 4w} \right)\left( {5{x^2} - 11xw} \right) & = 35{x^3} - 77{x^2}w + 20{x^2}w - 44x{w^2}\\ & =35{x^3} - 57{x^2}w - 44x{w^2} \end{split}
Simplifying (by Recognizing “1”) when dividing—
- \begin{split} \frac{{30{x^6}{y^9}}}{{15{x^6}{y^5}}} & = \frac{{2 \cdot 15{x^6}{y^5}{y^4}}}{{15{x^6}{y^5}}}\\ & = \frac{2}{1} \cdot \frac{{15{x^6}{y^5}}}{{15{x^6}{y^5}}} \cdot \frac{{{y^4}}}{1}\\ & = \frac{{2{y^4}}}{1}\\ & = 2{y^4} \end{split}
Finding a Common denominator and combining/separating—
- \begin{split} \frac{{x{y^2}}}{3} - \frac{{x{y^2}}}{7} & = \frac{{7x{y^2}}}{{21}} - \frac{{3x{y^2}}}{{21}}\\ & = \frac{{4x{y^2}}}{{21}} \end{split}
- \begin{split} \frac{3}{t} + \frac{{4t}}{r} & = \frac{{3r}}{{tr}} + \frac{{4{t^2}}}{{tr}}\\ & = \frac{{3r + 4{t^2}}}{{tr}} \end{split}
- \begin{split} \frac{{6{x^3}y - 22{x^4}{y^2}}}{{2x}} & = \frac{{6{x^3}y}}{{2x}} - \frac{{22{x^4}{y^2}}}{{2x}}\\ & = 3{x^2}y - 11{x^3}{y^2} \end{split}
Practice
Ask a friend to think of any integer and add the next highest integer to it. Tell him to add 13 to that result, and then divide by 2. Finally, he subtracts the original number he thought of. What will his final answer be? Why?
Have a friend select two secret numbers of their choosing—call them Rosencrantz and Guildenstern.
Have them triple Rosencrantz, and then add 15 to their result.
Then have them multiply Guildenstern by 6, and add 21 to their answer.
Have them compute (Answer for Part a) - (Answer for Part b).
Tell them to divide their answer for Part c by 3. Let’s call this number “Hamlet”.
Ask them to add 2 to Hamlet, then to subtract Rosencrantz, and finally to tell you the number they’ve calculated.
Tell them you now know what Guildenstern is—because you do! Just divide the number they tell you in Part e by $-2$, and that is equal to Guildenstern. Why does this trick work?
If your friend told you “Hamlet” as well, you could also figure out what Rosencrantz is. Why? Explain.
Here’s one that involves powers. Again, pick a number.
Double it, and then raise your answer to the 3rd power. Call what you get “Jack”.
Now instead, multiply the original number by 6, and then square the result. Call what you get “Jill”.
Compute $\frac{{{\rm{Jack}}}}{{{\rm{Jill}}}}$, and then multiply that by 4.5.
What in the world is going on?
Use the distributive property to help rewrite the expression so that it is as compact as possible, often called “collecting like terms”:
$- 3(a + 4b) - 6(2b - a)$
$\left( {2x - y} \right)\left( {x + 3y - 7} \right)$
$\frac{2}{5}\left( {4m - 3n} \right) + \frac{3}{{10}}\left( {7m + n} \right)$
${\left( {j - k} \right)^2} - {\left( {j + k} \right)^2}$
Distribute and collect like terms.
$2x( - 3{x^2} - 4) - 2({x^3} - 4x + 7)$
$(4x{y^2} + 2x - 3y)(5{y^2} - 7{x^2} + 6)$
$\frac{{( - 6w - 4)( - 8w)}}{2}$
$- 12(3a - 2b) - 4\left( {7a - \frac{{3b}}{2}} \right)$
$3\sqrt x (\sqrt x + 4) - 7x(x - 5) - 12\sqrt x $
${\left( {2k - 3} \right)^2}$
Add or subtract by finding a common denominator, then collect like terms:
$\frac{{7x}}{8} - \frac{{8x}}{7}$
$\frac{{3x + 2}}{y} - \frac{{4y - 6}}{x}$
$\frac{{3{w^2} - 7u}}{{4u}} + \frac{{6u + 9w}}{{5w}}$
Separate the following fractions into separate terms, then simplify each term:
$\frac{{6x - 18y}}{3}$
$\frac{{5h{g^3} - 10{h^2}{g^5}}}{{5h{g^2}}}$
$\frac{{8{x^2} - 12xy + 20{y^2}}}{{ - 4xy}}$
$\frac{{14{y^{ - 3}} - 26{y^4}{z^{\frac{3}{2}}} + 10{z^{ - \frac{5}{2}}}}}{{4{y^3}{z^{\frac{1}{2}}}}}$
Simplify each of the following by recognizing “1”:
$\frac{{30{x^7}{y^4}}}{{18{x^6}{y^4}}}$
$\frac{{48{p^{24}}{q^8}}}{{36{q^{24}}{p^8}}}$
$\frac{51x^{-6}y^3z^0}{17{x^{-7}}{y^5}z^{-2}}$
$\frac{{42\sqrt z {y^3}{p^{\frac{5}{2}}}}}{{14{p^{\frac{1}{2}}}{y^4}\sqrt z }}$
If $\frac{{x + 5}}{{x + 1}} = 1 + \frac{M}{{x + 1}}$,
what number must $M$ be?
(Appeared on Algebra 1 Math Contest, 1995-6, #4)
Are the following pairs of expressions always, sometimes, or never equal? If the answer is “sometimes”, also find all the values of $x$ when they are equal.
$3 - 4x \ $ and $\ 4(6 - 2x) + 7(x - 3)$
$2{x^2} + 6x - 36 \ $ and $ \ 2(x - 3)\,(x + 6)$
$2(2{x^2} - 18) \ $ and $ \ \frac{{(2x - 6)(2x + 6)}}{{(x + 17)}}$
$4 - 2x - 3(5 - 4x) \ $ and $ \ - 4(3 - x) - 2(x - 3) + 7$
For each of the following equations, say whether it is an identity, meaning that it is true for all values of the variable(s). Check by assigning numbers to the variables in the equation and seeing if your answer still seems correct!
$\left( {x + y} \right)\left( w \right) = \left( {xw} \right)\left( {yw} \right)$
${a^{ - b}} = - \left( {{a^b}} \right)$
$4x + 3x = 7{x^2}$
${b^r}{b^s} = {b^{rs}}$
${\left( {a - b} \right)^2} = - 2ab + {a^2} + {b^2}$
${a^4}{b^3} = {\left( {ab} \right)^{12}}$
$2 + 3x = 5x$
${a^{ - 2b}} = \frac{1}{{{a^{2b}}}}$
${j^p}{j^q} = {j^{\left( {p + q} \right)}}$
$\frac{{5 + a}}{{5x}} = \frac{{1 + a}}{x}$
${\left( {j - k} \right)^2} > - 2$
$\left( {\frac{{5m - n}}{n}} \right) - \left( {\frac{{12n + 3m}}{{2m}}} \right) = \left( {\frac{{10{m^2} - 5mn - 12{n^2}}}{{2mn}}} \right)$
If ${\left( {{4^{ - 1}} - {3^{ - 1}}} \right)^{ - 1}}$ were to be rewritten as a single number, what would it be? (No calculators on this one!)
Simplify the following (and show the steps you took):
$\frac{{54{x^8}{y^{ - 3}}}}{{27{x^2}{y^{ - 6}}}}$
$\big(\frac{76x^5w^{-7}}{19w^{-4}x^8}\big)^{-4}$
$\big(\frac{p^{-3}}{12q^{-2}}\big)^{-1}$
$\big(\frac{120x^{-8}y^7}{y^{-2}x^{-4}w^3\cdot 15}\big)^{-2}$
$\big(\frac{x^{3n}y^6}{y^2x^n}\big)^{-2}$
Problems
Given that $(x + 2)(x + b) = {x^2} + cx + 6$ for all
values of $x$, what must $c$ be?
(Appeared on AHSME 1988 competition, #5)
If $Q = 2(3\pi - 7)$, how many times bigger than $Q$ is $8(12\pi - 28)$?
A tree broke at a point $\frac{1}{4}$ the distance up the trunk, and when it fell the top of the tree was 60 feet from its base (so a triangle is formed — the upright $\frac{1}{4}$ of a tree, the diagonal rest of the tree, and the ground). How tall was the tree?
If $x = {y^2}$, what is the value of ${y^{1996}} -
{x^{998}} + 499$?
Copyright www.mathleague.com.
$f$ is a function that squares a number, then adds 16. $g$ is a function that adds 4 to a number, then squares the result. Anthony says that $f$ and $g$ are really the same function. Is he right?
Prove that the square of an even number is always even. Then prove that the square of an odd number is always odd. (Hint: Every even number is a multiple of 2; every odd number is one more than a multiple of 2.)
Prove that the square of an odd number minus the square of another odd number is always a multiple of 4.
Take two numbers: the first should be a multiple of 12, and the second 3 more than the first. Prove that the second number squared minus the first number squared will never be divisible by 6.
If $\frac{1}{{x - 1}} - \frac{1}{{x + 1}} = \frac{C}{{{x^2} - 1}}$, what number must $C$ be?
A box whose dimensions are 4 ft, 4 ft and 4 ft. is packed with cylindrical cans that are 2 ft high with a diameter of 6 in. When the box is fully packed with cans, how much space is wasted in the box? Prove that your answer is the same as $16(4 - \pi )$ ft$^3$.
If $a + b = 0$, but $a \ne 0$, what is the value of
$\frac{{{a^{2007}}}}{{{b^{2007}}}}$?
Copyright www.mathleague.com.
The length (in cm) of the diagonal
connecting opposite corners of a cube is the same as the
volume of the cube (in
cm$^3$). What is the surface area of the
cube?
Three adjacent faces of a rectangular box have areas 20, 30, and 40 cm$^2$. What is the exact volume of the box?
Make up a problem like Problem 2 and try it out on your classmate. Make sure to prove that it works before doing it!
This trick involves two numbers — your age, and the amount of change in your pocket (expressed in pennies — a number from 1 to 99).
Double your age.
Add 5.
Multiply by 50.
Add the amount of change in your pocket (and if you don’t have change, just think of a number between 1 and 99).
Subtract the number of days in a non-leap year.
Add 115.
Divide by 100.
Look to the left and to the right of the decimal point. Cute, no? How does this one work?
Here’s a trick for you to finish. Take two positive numbers, $x$ and $y$.
Multiply their sum by their difference.
Now multiply your answer by the sum of their squares.
Add $y$ raised to the 4th power.
Take the square root of your result.
How could someone always figure out what “$x$” was if they had the answer to Part d?
Pick two numbers.
Multiply the first by three more than the second — call it “Sonny”.
Multiply the first by three less than the second — call it “Cher”.
Subtract Cher from Sonny, and then divide by 6. What do you notice?
Now add Cher to Sonny, and then divide by double the first number. What have you found?
Explain the mysteries of Sonny and Cher. (It might help to think of the two numbers you picked at the start as $x$ and $y$.)
John from Cincinnati claims that he has a snappy way to calculate ${37^2} - {33^2}$ in his head — just multiply the sum of the two numbers by their difference (i.e. $70 \cdot 4 = 280$).
Does John’s method actually work? Try it on a few pairs of numbers.
If two numbers that you pick are $x$ and $y$, John’s method claims that there is an easier way to calculate $x^2- y^2.$ In terms of $x$ and $y$, what is John saying is the easier way?
Prove that John’s method always works, or that it doesn’t always work.
Calculate $104 \cdot 96$ in your head! (Hint: Work backwards!)
Distribute $(2w - 12z)(2w + 12z)$ and $(x^3+y^7)(x^3-y^7)$; what do you notice?
Jake made up the following number trick, which he was sure would dazzle all his friends. “Pick a number without telling me. Multiply it by 100, and subtract that from 2500. Now add the square of the original number, and tell me the answer.” Jake knew that all he had to do was call the final result $Y$, use his calculator to compute $50 - \sqrt Y $, and he’d have their original number back.
Confirm that Jake’s method works for a few numbers. Then explain why it works.
For a while, Jake’s trick worked wonderfully. But the other day, his friend Rachel said that Jake had failed to read her mind! Her number had been 99, but Jake had guessed 1. How could he have been so hideously far off?
Phil from Duluth has another calculating trick. He says that he can calculate $33 \cdot 27$ in his head by taking the square of the sum of the two numbers and subtracting the square of their difference, and then dividing the answer by 4: $\frac{{{{(33 + 27)}^2} - {{(33 - 27)}^2}}}{4}$. This is quicker, Phil points out, because the numbers are easier—
$\frac{60^2-6^2}{4} = \frac{60^2}{4} - \frac{6^2}{4} = 900 - 9$is a lot easier to calculate in one’s head than $33 \cdot 27$.
Is Phil correct that this method always gives the right answer? Will this always work with any two numbers? Prove your answer.
Is Phil correct that this method is always quicker? Give some examples to back up your position.
A terminating decimal is a decimal like $.3764$, which ends. A repeating decimal is one that repeats forever, like $.862862862... .$
How can one express any terminating decimal as a fraction? Show that you can do so with $.3674$ and $.1864597.$
It isn’t obvious whether repeating decimals can be expressed as fractions or not. Still, if $.862862862...$ were to be equal to a fraction, it would have to be close to $\frac{{862}}{{1000}}$. See if you can find a fraction which appears to do better.
Will the idea of part b work with any repeating decimal? Try it out on $.9166591665...$ and $.333... .$
Let $x =.333... .$ By multiplying both sides of this equation by 10, one gets a new equation. By combining equations, prove why $.333... = \frac{1}{3}$.
Now prove that $.862862862...$ is a fraction as well by a similar method to part d. Will this method let you convert any repeating decimal into a fraction? Does it work on $.9166591665...,$ for example?
Don’t use a calculator for this problem.
Factor $x^2-x+12$.
Solve ${x^2} + 4x + 2 = 0$ by completing the square.
Divide $5.\bar 3 \div 8$.
Simplify $\sqrt{50a^4b^3}$.
If $(x - 2)(x + 2) = 5$, find ${x^4} - 4{x^2}$.
Ask a friend to think of a three-digit number in which the
digits are all the same (such as 777). Tell them that you
don’t want to know the number, but that you would like them
to add up the digits, multiply by 37 and tell you the answer.
Why would they think you are being a wiseacre? Can you prove
it always “works”?
(Hint: $777 = 700 + 70 + 7 = 7\left( {100 + 10 + 1} \right)$.)
If I have a larger number divisible by 3 and subtract a smaller number divisible by 3, will the answer necessarily be divisible by 3? Try some examples. Explain why what you have found makes sense.
If I have a larger number and subtract a smaller number divisible by 3 and get an answer that is divisible by 3 — is the larger number necessarily divisible by 3? Again, try some examples, and explain why your conclusions are justified.
After having completed and digested the ideas of Problems 44 and 45, we are now ready to understand why the divisibility test for 3 works. Remember that the divisibility test for 3 states that if the sum of the digits of a number is divisible by 3, then the number itself is as well. (You will prove below that it works for a three digit number, but your proof can be adapted easily to any number of digits.)
We can write 741 in the following way: $700 + 40 + 1$, and similarly we can write 6518 as $6000 + 500 + 10 + 8$. How could you write any number “ABC” in the same way, where A is the hundreds digit, B is the tens digit, and C is the units digit?
Consider 568, which is not divisible by 3. Notice that when you subtract the sum of its digits (5 + 6 + 8 =19) from itself, the answer you get, 549, is divisible by 3. Does this always work for any 3-digit number?
Use algebra to prove the result you found in part b. Your answer to part a. will be helpful here.
If $\left( {{\rm{A + B + C}}} \right)$ is also divisible by 3, by using what you learned in Problem 45 and parts b and c above, what can you now say about the number “ABC"? Explain!
If $\left( {{\rm{A + B + C}}} \right)$ is not divisible by 3, what, if anything, can we say now about “ABC”? Explain carefully.
Pick a 3-digit number. If one subtracts the “reverse” of the number from the number itself, the answer is always a multiple of 9. For example $852 - 258 = 594$, which is a multiple of 9 (and negative numbers “work” as well — e.g. If we had picked $258, \ 258 - 852 = -594$). Explain why this is so. (Remember that any three digit number “ABC” can be written as $100{\rm{A}} + 10{\rm{B}} + {\rm{C}}$ ; how do you think you could write its reverse, “CBA”?) Will this work for 4 or 5 digit numbers as well?
Go to the following web page and have fun!: http://digicc.com/fido/ What is going on here? Can you come up with an explanation of how it is done?
Look at the following YouTube video on the method of “Vedic Multiplication”: www.youtube.com/watch?v=gwaAAEYIW_8 Why does this method work? Will it always work?
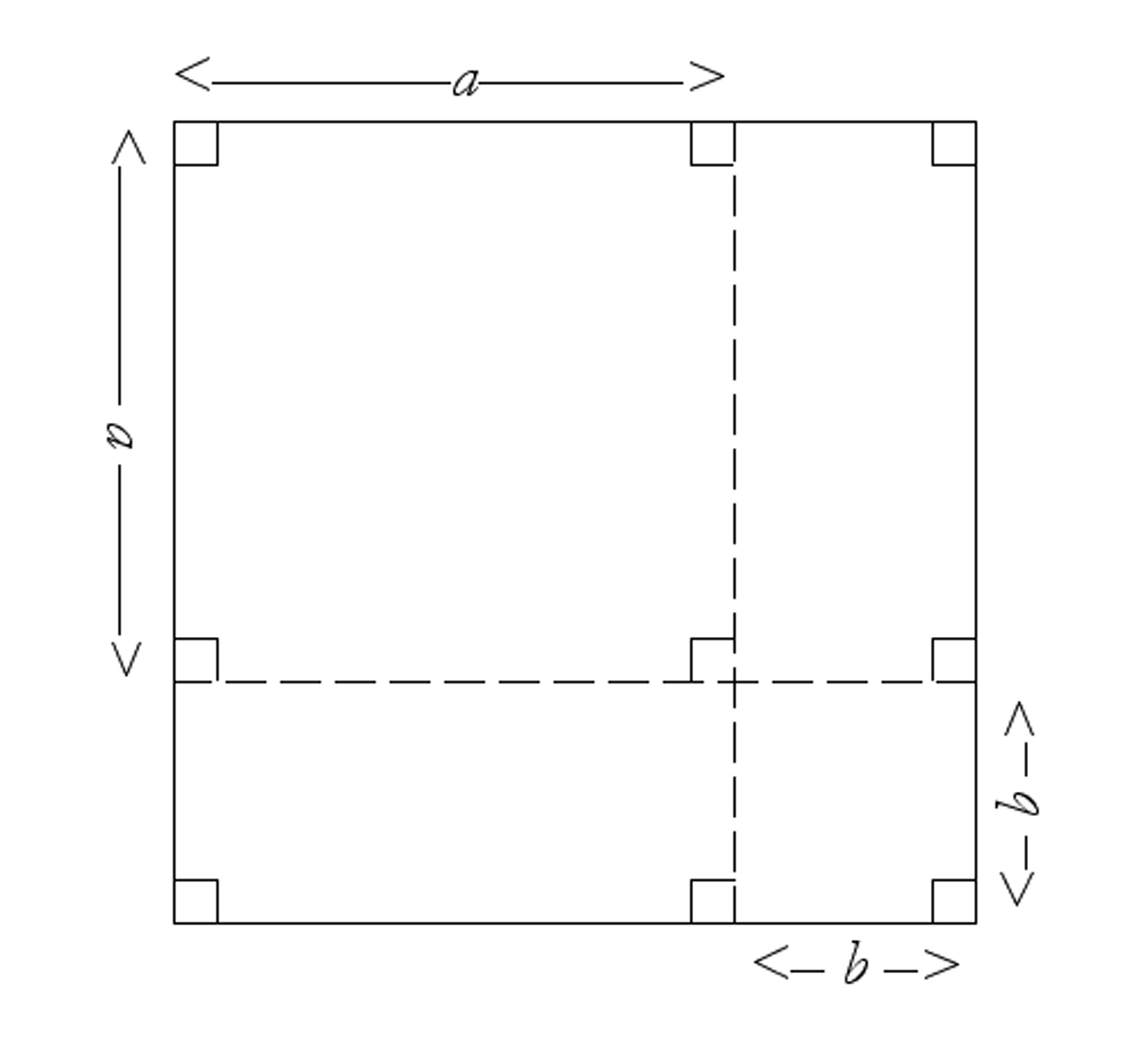
Explain what the following “Proof without Words” is equivalent to algebraically:
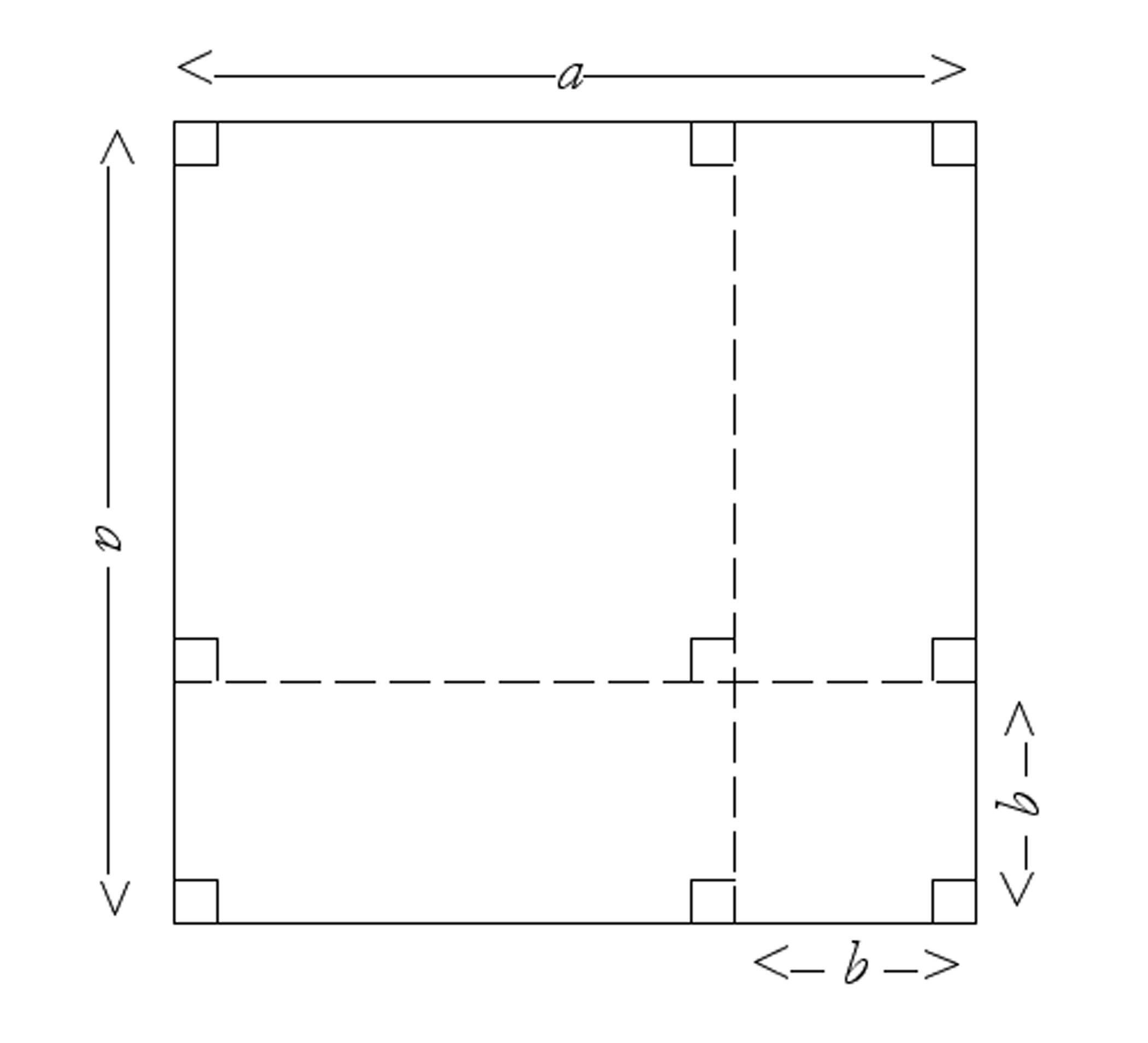
Explain what the following (slightly harder) “Proof without Words” is equivalent to algebraically:
Exploring in Depth
Is the sum of 3 consecutive integers always divisible by 3? Is the sum of 4 consecutive integers always divisible by 4? Is the sum of 5 consecutive integers always divisible by 5?
When is the sum of $n$ consecutive integers divisible by $n$? Try different values of $n$ to get a feel for the problem, and then see if you can give good reasons for the pattern you see.
Prove that the square of an odd number is always one more than a multiple of 8. (Hint: Try factoring part of the expression you came up with to represent the square of an odd number, and also note that with any two successive integers, one of them must be odd and one of them must be even.)
Which primes can be expressed as the difference of two squares? Why? Can any be written as the difference of two squares in two different ways? Why or why not?
Here’s a quick way of multiplying any two 2-digit numbers, like 52 and 58, that have the same tens digit and have units digits that add up to 10.
- Multiply the tens digit by the next largest integer and call it “$M$” (here, $M = 5 \cdot 6 = 30$).
- Multiply the units digits of the two numbers together and call it “$N$” (here, $N = 2 \cdot 8 = 16$).
- Write the digits of $M$ followed immediately by the digits of $N$ (here, 3016). This gives you the right answer!
Why does this work?
Four whole numbers, when added three at a time, give the following sums: 188, 199, 212, and 220. Find the four numbers.