Introduction: Hey batta! Hey batta!
Jan bats .500 in softball — i.e., on average, for each 10 at-bats she gets five hits. We wish to determine the probability that she will get no hits if she comes to bat 5 times during a game. In order to calculate this probability we must assume that she stays a “.500 hitter” from one at-bat to the next, which is to say that success or failure at each at-bat is not affected by the previous at-bats. Given this assumption we can perform the following calculation:
Probability of no hits in 5 at-bats = $ \frac{\text {number of ways of getting no hits in 5 at-bats}}{\text {number of possible outcomes in 5 at-bats}}$
= $\frac{1}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 2}$
= $0.03125$
What is the probability that Jan will get exactly one hit in 5 at-bats?
What’s the probability that Jan will get exactly 4 hits in 5 at-bats?
What’s the probability that Jan will get exactly 2 hits?
The last question probably took some time to calculate since there are 10 different ways for Jan to get exactly 2 hits. For example, one string of at-bats might look like HNHNN, where H = “hit” and N = “no hit”. Imagine trying to calculate the probability that Jan would get exactly 3 hits in 10 at-bats. Don’t do this by listing all the strings of 10 at-bats with 3 hits. You will be cursing by the end of this process, if not earlier. Fortunately, there is a more elegant way of counting how many strings have exactly 3 hits in 10 at-bats. Let’s look at one approach.
Development
This approach will require us, first, to review two basic counting principles that you learned last year. Suppose you’re setting up a password for a new account.
If the password must be 3 letters followed by 3 digits, then how many possible passwords are there? The password is not case-sensitive so there’s no distinction between “a” and “A”.
If the password must be 3 letters followed by 3 digits, but no letter or digit can be repeated, then how many passwords are there? Again, the passwords are not case-sensitive.
If the password must be 10 digits, no letters, with no repetition, then how many passwords are there? There’s a nice shorthand way of writing this answer. Do you remember it?
The problems above involve a basic principle of counting called the Multiplication Principle of Counting. You also needed to pay attention to whether repetition mattered. Lastly, Problem 6 alludes to some shorthand notation that comes in handy when the final count gets very large. Keep in mind that this is only notation and doesn’t solve problems for you. As you progress through this lesson, you’ll need to remember that the formulas you might derive are not all-purpose ones that solve counting problems. They tend to work in highly specialized situations. You will find more success if you read each problem carefully, think about what is being counted (visualize, even), and then apply basic principles like the Multiplication Principle of Counting. Now, let’s see how to tackle the batting problem by looking at a similar problem.
The word error has 5 letters in it, two letters that appear once and one that appears three times. We’re going to look at different 5-letter “words” that can be formed by rearranging these 5 letters. These words need not make any sense, so “rroer” is a word.
How many 5-letter words can be formed, assuming that you can tell the difference between the $r$’s? In other words, think of the $r$’s as being a red $r$, a blue $r$, and a green $r$ (or as ${r_1}$, ${r_2}$, and ${r_3}$). By the way, each of the letters can only be used once per word.
Write down two 5-letter words that differ from each other only if the $r$’s are different colors. How many other 5-letter words differ from these two only if the $r$’s are different colors?
Think of another 5-letter word that is different from the ones in Part b. How many versions are there of this 5-letter word that are distinguishable from each other only if the $r$’s are different colors? Would all of these 5-letter words be part of the count you made in Part a?
So, how many 5-letter words can be formed by rearranging the letters in error, if each letter can only be used once per word (and the $r$’s are indistinguishable from each other)?
Lastly, you should be able to write your answer to Part d in the form $\frac{5!}{n!}$. What is $n$?
How many distinguishable 9-letter words can be formed from the letters in freestone, where each letter can only be used once per word?
How many distinguishable 9-letter words can be formed from the letters in freewheel, where each letter can only be used once per word?
How many distinguishable 9-letter words can be formed from the letters in appraisal, where each letter can only be used once per word?
Using the letters H, H, H, H, H, N, N, N, N, N, N, N only, how many 12-letter words can be formed? (Note: though the word “distinguishable” is not appearing you should assume you are just counting words that are different from each other.)
In the previous problems you were always counting letters. If you think about what you were doing, however, you should realize that the method of counting wasn’t dependent on letters. Problem 11, for example, could have initially been a problem about how many ways can you step right five times and left seven times in a sequence of twelve steps.
Bill is flipping a coin 8 times, keeping track of the sequence of heads and tails. What is the probability that he’ll get exactly 5 heads in total? Exactly 4 heads? 3 heads?
Alix’s mathematics class wants to form a committee of 4 students to investigate whether AP classes should be taught in the school. If there are 16 students in the class then how many different committees can be formed?
The last problem may have seemed quite different from the previous ones, but there is a way of seeing it as no different. Imagine that you’re working with all 16 students and that you have 16 Velcro labels. Twelve of these labels are a large N and four of them are a large Y. You line the 16 students up and then try to count how many different ways you can assign the labels to the students. In this sense, you are trying to determine how many different ways you can arrange 12 N’s and 4 Y’s in a sequence.
The answer to the last sentence (and to Problem 13) can be written in the form $\frac{{a!}}{{b!{\kern 1pt} {\kern 1pt} {\kern 1pt} c!}}$, where $a$, $b$, and $c$ have specific meanings in the context of the problem. What are $a$, $b$, and $c$ and what are their meanings?
The fraction in Problem 14 can be simplified so that there is only one factorial expression in the denominator. Do this.
Look back at your answer to Problem 15 and remember that this fraction is an answer to Problem 13. Now, use your understanding of the relationship between this fraction and Alix’s committee problem to answer the following question.
You’re going to order a triple-scoop bowl of ice cream. If you plan on choosing three different types of ice cream from 8 possible choices, then how many different triple-scoop combinations are there?
In this lesson you have seen some problems where two different orderings of the same things are to be thought of as being different — e.g., the passwords 3857210964 and 6710892534. In other problems, you’ve had to discount these differences — e.g., the triple-scoop combination of chocolate-vanilla-pistachio does not differ from the combination pistachio-chocolate-vanilla. As you work through the remaining problems in these lessons, bear in mind these distinctions. Some problems will fall into one category and not the other, while some will fall into both. And, of course, some will fall into neither.
Practice
John and Mary are ordering hamburgers that come with 3 types of toppings: cheese (cheddar, blue, swiss), vegetable (lettuce, onion, tomato, mushroom), and sauce (mustard, ketchup). They will each order one of each type of topping.
John doesn’t care about the order of his toppings, figuring that the whole mess ends up in the same place. How many different burgers does John think he can order?
Mary believes very strongly that the order in which the toppings are on her burger does subtly change the taste of the hamburger. How many different burgers does Mary think she can order?
There are 8 books on a shelf — five novels and three biographies. How many different ways can you line the books up on the shelf if
you naturally think of the books as being different from each other?
you don’t distinguish the novels from each other or the biographies from each other, but you do distinguish novels as different from biographies?
You shuffle a standard 52-card deck several times.
How many different sequences of 5 cards are there at the top of the deck?
You deal a hand of 5 cards to yourself. How many possible 5-card hands are there?
Estimate the amount of time it would take to create all the possible 5-card hands of part b, assuming you can create 1 new hand every second. Would it take a day, a week, a month, a year, or a decade, or longer? What if you were trying to create all the possible 7 card hands? What about all the possible 52 card hands? Check your 3 estimates with a calculator and see if you were right in each case within a factor of 10 (also known as an “order of magnitude”).
A true-false test has 25 questions on it. If you take the test by randomly deciding that 10 of the questions are true and the rest are false, then how many ways can you write down the answers to the test?
How many different ways can you arrange the letters in Mississippi?
Horatio has 3 tulips, 4 irises, and 3 daffodils growing in his yard. For each of ten days, he cuts one flower and brings it to his math teacher. How many ten-day sequences of flowers are there? (An example of one such sequence is iris-tulip-iris-iris-daffodil-tulip-daffodil-daffodil-tulip-iris.)
Using the seven digits 9, 9, 9, 3, 3, 3, and 3, once each, how many 7-digit numbers can be formed?
Each of the 240 students attending an Upper School dance has a ticket with a number for a door prize. If three different numbers are randomly selected, how many ways are there to award the prizes if the prizes are different from each other? if the prizes are identical?
In how many ways can you choose 3 letters from the word problems, if the order in which you choose the letters is important? is unimportant?
Problems
There are 20 cities in a certain country, and every pair of them is connected by an air route. How many air routes are there?
Remember Jan who bats .500 in softball. What’s the probability that she will get exactly 4 hits in 10 at-bats? What’s the probability that she will get no more than 4 hits in 10 at-bats?
How many “words” can you form from 5 A’s and no more than 3 B’s?
There are 6 books on a shelf. How many ways are there to arrange some (or all) of the books in a stack? The stack may consist of one book.
A teacher has a collection of 40 true-false questions. She wishes to create a test using 5 of these questions. How many different tests can she create if
the order of the questions doesn’t matter?
the order of the questions does matter?
How many three-letter words can be formed from the letters A, B, C, D, E, F, G, H, and I, where each letter can only be used once per word?
The points A, B, C, D, E, F, G, H, and I are vertices of a regular polygon. If three of the points are chosen, and connected by line segments, a triangle is determined. How many triangles can be formed in this way? If four points were chosen to form a quadrilateral, then how many such quadrilaterals will there be?
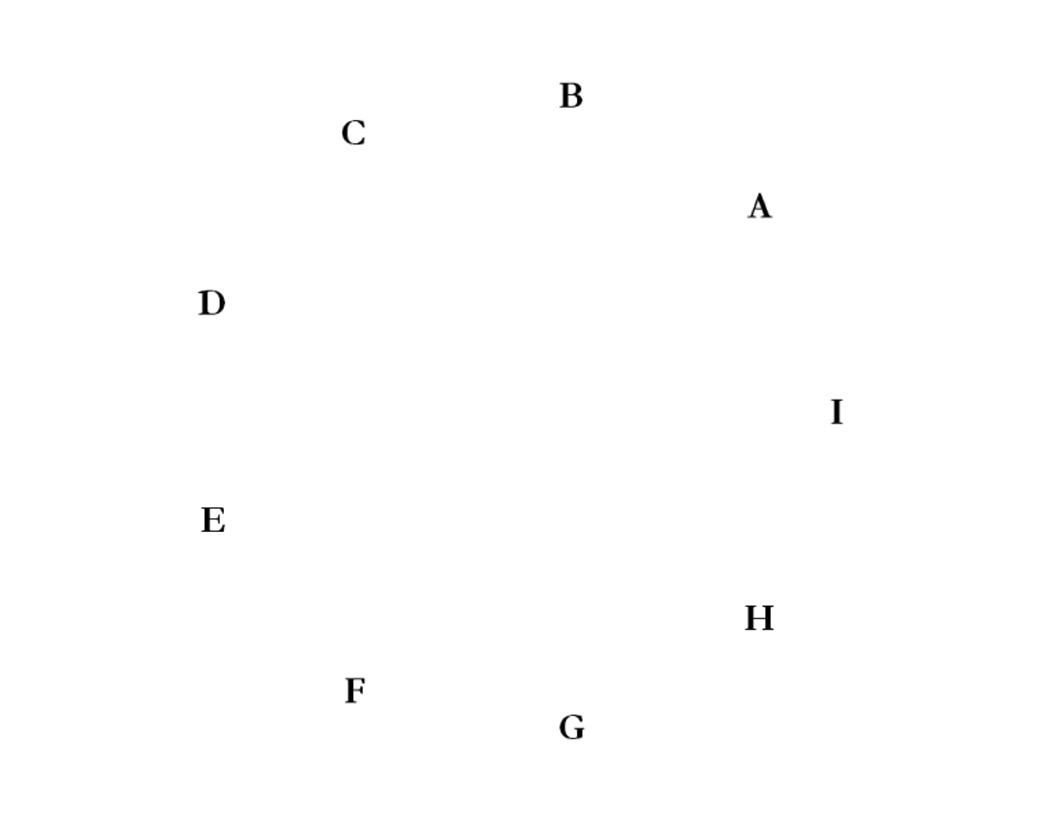
You have six sticks of lengths 1, 2, 3, 4, 5, and 6 inches. How many non-congruent triangles can be formed by using three of these sticks as sides?
There are three rooms in a dormitory: one single, one double, and one for four students (called a “quad”). How many ways are there to house 7 students in these rooms?
Creamy Heaven serves 30 different ice cream flavors. A customer can order a single-, double-, or triple-scoop cone.
How many double-scoop cones are there if both scoops can be the same flavor and the order of the scoops doesn’t matter?
How many possible cones are there if flavors can be repeated and the order of the scoops doesn’t matter?
Three couples go to the movies and sit together in a row of seats. How many ways can they arrange themselves if each couple sits together?
Eight people are at Chen’s house for a party (Chen is one of the eight). Chen has several options for sitting people for dinner.
If Chen gets a long table she can sit people on one side of the table so that they can watch a movie while they’re eating. How many ways can she sit the eight people in this situation?
Chen can get a shorter, but rectangular table, and sit four people on one side and the other four on the opposite side. How many ways can she sit the eight in this situation? Assume that two arrangements that are reflections of each other over the long axis of the table are indistinguishable from each other.
Chen can sit the eight around a circular table. How many ways, now? Assume that two arrangements that are rotations of each other are indistinguishable from each other.
If Chen sits $n$ people around a circular table, then how many ways can this be done if two arrangements that are rotations of each other are indistinguishable?
A bug jumps from lattice point to lattice point on a piece of graph paper according to the following pattern: from $\left( {a,b} \right)$, the bug can jump only to $\left( {a+1, b} \right)$ or to $\left( {a, b+1} \right)$. How many different paths can the bug take if it wishes to start at $\left( {0,0} \right)$ and end up at $\left( {6,4} \right)$? Hint: tinker with this problem a bit so that you can get a feel for what the bug is doing.
Homer starts at the origin and performs a five-step random walk along a number line. Each second he steps either one unit to the left or one unit to the right.
Describe all the places that Homer can wind up at the end of this walk.
How likely is Homer to end up 5 steps to the right? 3 steps to the right?
If Homer were to perform this 5-step random walk 32000 times, what is your prediction of the average of all the final positions? What is your prediction of the average of all the distances from the origin to Homer’s final position?
How many diagonals are there in a pentagon? a hexagon? a
decagon? an
The rules of a checkers tournament indicate that each contestant must play every other contestant exactly once. How many games will be played if there are 12 participants? How many will be played if there are $n$ participants?
Don’t use a calculator for this problem.
Reduce the fraction $\frac{6a^2}{4a^2-6a}$.
Solve for x: ${x^2} - 5x = 14$.
Solve for x: ${x^2} - x - 1 = 0$.
Divide $\frac{2}{x} \div \frac{4}{{{x^2}}}$.
Write as one fraction: ${\left( {\frac{b}{{2a}}} \right)^2} - \frac{c}{a}$.
How many ways can you split up 12 people into six pairs?
You have learned that any positive integer has a prime factorization of the form ${2^a} \cdot {3^b} \cdot {5^c} \cdot {7^d} \cdot {11^e} \cdot {13^f}...$, where the “…” represents the rest of the primes, and $a$, $b$, $c$, $d$, $e$, $f$, and so on can each equal 0, 1, 2, 3, … . So for example, 360 is equal to ${2^3} \cdot {3^2} \cdot {5^1}$.
Remembering that every possible factor of 360 comes from one of the possible combinations of these prime factors (e.g. $20 = {2^2} \cdot {3^0} \cdot {5^1}$ and $90 = {2^1} \cdot {3^2} \cdot {5^1}$), and using the principles of counting that you learned studying combinatorics, determine the number of factors that 360 has. Note that 1 is considered a factor of 360 in this problem, i.e. $1 = {2^0} \cdot {3^0} \cdot {5^0}$. (You might try answering for 84 instead of 360 if you want an easier example to start with.)
Generalizing Problem 44, find a way to determine the number of factors that any positive integer has. Try out your method with at least 3 other positive integers to check to see if it works.
Let $n \choose r$ stand for $\frac{{n!}}{{r!\left( {n - r} \right)!}}$, where $n$ and $r$ are nonnegative integers, and $r \leq n$.
Calculate $6 \choose 2$.
Calculate$7 \choose 1$.
Is $n \choose r$ ever not an integer? Explain.
Prove: $\frac{n(n-1)(n-2) \cdots (n-r+1)}{r(r-1)(r-2) \cdots 2 \cdot 1} = {n \choose r}$.
Determine what should replace
the question mark so that the
following statement is true, then prove that the statement is
true:
${n+1 \choose r} = {? \choose r-1} + {? \choose r}$
Exploring in Depth
How many different 5-person basketball teams can be chosen from a group of 10 people? How many ways can you split up 10 people into two different 5-person basketball teams?
The points A, B, C, D, E, and F are vertices of a regular hexagon. What is the probability that three randomly chosen vertices from this hexagon will form an equilateral triangle? What’s the probability that four randomly chosen vertices from this hexagon will form a rectangle?
This is a continuation of Problem 38. In this problem you will see a connection between algebra and counting.
Expand ${\left( {r + u} \right)^5}$ and explain how this can help you determine how many paths there are from $\left( {0,0} \right)$ to $\left( {2,3} \right)$. Recall that when simplifying and collecting expressions such as $rru$, $rur$, and $urr$, we can write the final result as $3{r^2}u$.
What expression can you expand and simplify in order to answer Problem 38?
What is the coefficient of the ${x^3}{y^5}$ term in the expansion of ${\left( {x + y} \right)^8}$?
What is the coefficient of the ${x^5}{y^7}$ term in the expansion of ${\left( {2x + y} \right)^{12}}$?
What is the sum of all the 3-digit numbers that can be formed using three different odd digits?
Box Problems You probably didn’t realize that there are combinatorial problems that involve boxes, but there are.
Four boxes are numbered 1 through 4. How many ways are there to put 8 identical balls into these boxes (some of the boxes can be empty)? Hint: Imagine that you have 12 slots to work with.
Four boxes are numbered 1 through 4. How many ways are there to put 8 identical balls into these boxes so that none of them is empty?
Below is shown a triangle of dots. Suppose you start at dot A and move down through the triangle in the following manner: from any dot you can only move to the next dot that is down left or down right. So, if you are at dot A you can move to either dots B or C, but not directly to D or E. Below each dot in the triangle write the number of distinct paths from dot A to that dot.
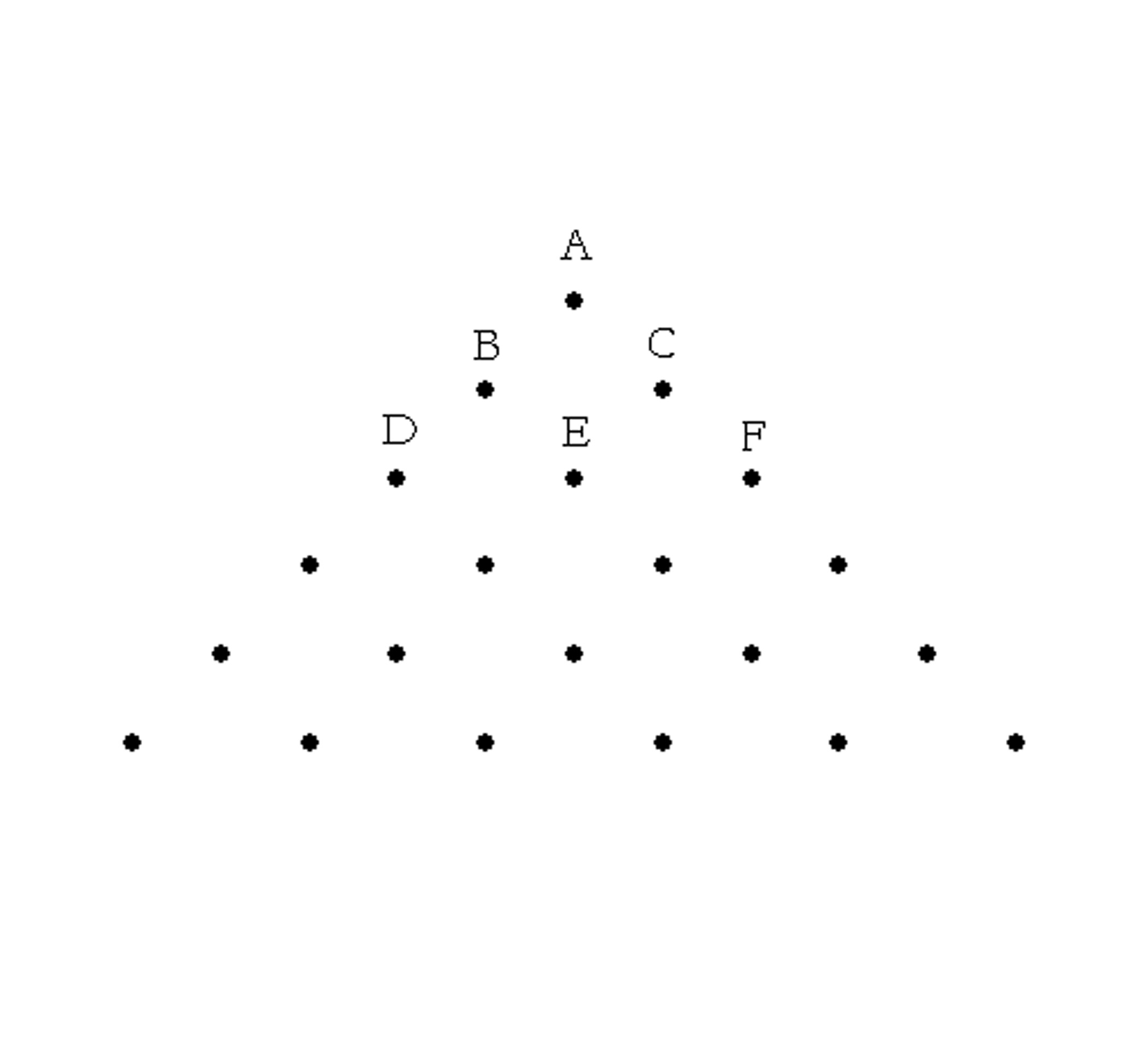
There is a well-known triangle called Pascal’s Triangle. What is this triangle and how does it relate to counting?