How many colors would it take to color each one of the graphs below? Explain your answer for each graph.

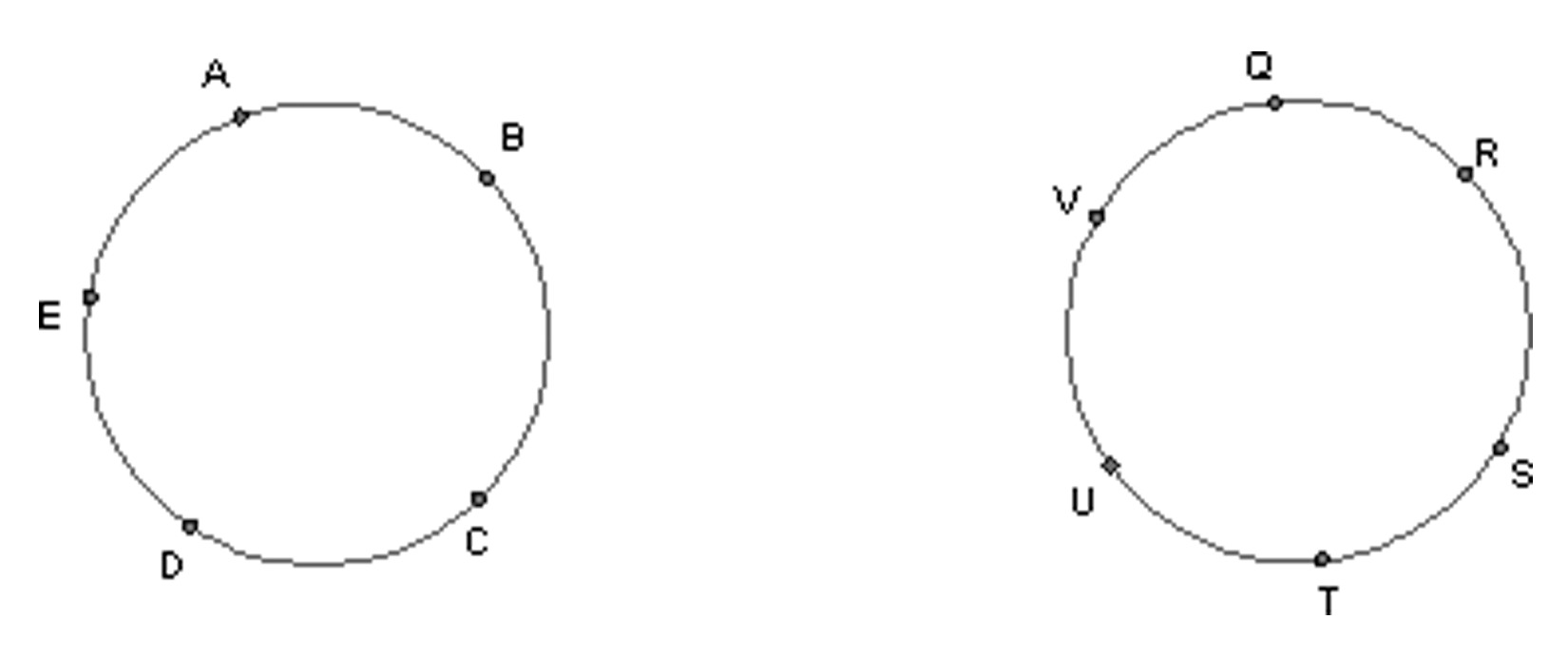
What if there were “$n$” nodes on the circle (instead of the 5 nodes and 6 nodes in the graphs of part a) — then how many colors would it take to color? Answer clearly and completely.

Chris draws a graph that has an Euler Circuit. Alonso adds an edge to Chris’s graph, and now, although the graph no longer has an Euler Circuit, Alonso says it has an Euler Path. Can Alonso possibly be right? Explain.

From Crisler and Froelich: Discrete Mathematics Through Applications. The following is a list of chemicals and the chemicals with which each cannot be stored.

Chemicals	Cannot Be Stored With
1	2, 5, 7
2	1, 3, 5
3	2, 4, 5
4	3, 7
5	1, 2, 3, 6, 7
6	5
7	1, 4, 5

Draw a graph to represent the situation.

How many different storage facilities are necessary to keep all 7 chemicals?

Uler says she just drew a graph with 1001 nodes, and exactly 500 of the nodes are of even degree. Do you believe her? Explain.

How many colors does it take to color a complete graph with n nodes? Explain.

A graph has 6 nodes with degrees 3, 3, 4, 5, 3, and 2. Is it possible for the graph to have an Euler path?

For each of the following say whether it’s true or false. If false, produce a counterexample or say precisely why.

Sum of degrees of any graph is even.

Every graph has an even number of nodes of odd degree.

If a graph has an Euler path then it must have exactly two vertices/nodes of odd degree.

Every graph of 4 or fewer nodes is planar.

All the nodes of a graph could be of odd degree.

A planar graph could be isomorphic to a non-planar graph.

All complete graphs with four nodes are isomorphic to each other.

For some graphs that have Euler circuits, it is actually still possible to walk around those graphs in such a way that you get stuck before you’ve crossed every edge. Draw one such graph, and show (a) how to walk around it so that you cross every edge exactly once, and (b) how to walk around it so that you get stuck before you get to every edge.

Simplify $\big(\frac{120x^{-8}y^7}{y^{-2}x^{-4}z^3 \cdot 15}\big)^{-2}$ making sure there are only positive exponents in your simplified answer.

Write the fraction in as simplified a form as possible, without using a calculator:
$\big(\frac{105/117}{165/363}\big)^{-3}$

If $x$ and $y$ are > 0, express $\frac{{{x^y}{y^x}}}{{{y^y}{x^x}}}$ , using only a single exponent.

Find the prime factorization of 533610. Use a calculator to help! Now, find the prime factorization of 20! (20 factorial), without a calculator.

How many of the first 200 positive integers are divisible by all of the numbers 2, 3, 4 and 5?

Suppose $p$ and $q$ are prime numbers.

What are all the factors of the number $pq$ ?

List all the factors of ${p^{10}}$ .

How about ${p^2}{q^2}$ ?

Write each of the following numbers in the form ${2^a}{3^b}{5^c}{7^d}$ , where $a$, $b$, $c$, $d$ can be whatever you want.

2100

$\frac{1}{{21}}$

2

1

2.1

Write the GCD of ${2^a}{3^b}{5^c}{7^d}$ and ${2^{a + 1}}{3^{b - 2}}{5^{c + 4}}{7^d}$ , assuming that $a$, $b$, $c$, $d$ have to be integers larger than 1.

Is $\frac{{50^{24}}}{{20^{12}}}$ , simplified, an integer or a
fraction? Explain.

Simplify the following expressions, and make sure there are no negative exponents:

$\frac{{36{{(x{y^4})}^{ - 2}}}}{{40{x^5}{y^{10}}}}$

$\big( \frac{(x^2y^{-3})^2}{x^{-2}y^5} \big)^{ - 1}$

. $\big(\frac{16^{-4}x^{-4}y^{-2}}{128^{-2}x^{-3}y^{-3}}\big)^3$

If $m \ne 0$ , then $\frac{{{{({m^4})}^4}}}{{{m^4}}} = $ …?

If ${4^{6x - 9}} = 64$ then what is the value
of $x$?

You ask your friend to do the following calculations:

Take a number

Add 1

Multiply by 3

Multiply your answer in (c) by one less than the original number …

When your friend tells you the answer in d, what’s the fastest process you can use to figure out what the original number was?

Another number trick:

Pick a number.

Double your number.

Square the result in “b”

Subtract 4. Call this answer “Fred.”

Now take your original number and add one.

Multiply this number by one less than the original number. This is “Lilli”.

What is $\frac{\rm{Fred}}{\rm{Lilli}}$ ? Why does this work?

You ask your friend to think of a number, then

• Multiply by 6

• Add 9

• Divide by 3

• Subtract 3.

Your friend tells you the answer. What do you need to do to get the original number back so that you can convince your friend you are a mind-reader? Show some algebra to explain why.

Which equation represents the following statement?
Twice the difference between a certain number and its square root is 15 more than twice the number.

$2N - \sqrt{N} = 15 + N$

$2\left( {N - \sqrt N } \right) = 15 + 2N$

$2N - \sqrt N = 16 + N$ )

$2N - \sqrt N + 15 = N$

$2\left( {N - \sqrt N } \right) + 15 = N$

$2N - 2\sqrt N = 15 + 2N$

Simplify the following so that there are only positive exponents: $\big(\frac{168p^{-4}q^5r^{-6}}{42pq^{-2}r^3}\big)^{-2}$

Simplify this until it is a single fraction that is reduced as much as is possible:
$\big(\frac{180 \cdot 5}{4 \cdot 196}\big) \cdot \big(\frac {448 \cdot 49}{1800 \cdot 15}\big)^2$

Simplify by multiplying out and collecting like terms.
(By the way, these specific expressions tend to show up very often in algebra.)

${(x + y)^2}$

${(x - y)^2}$

$(x + y)(x - y)$

$(1 + x)(1 - x)$

$(x + 1)(x - 1)$

Simplify by multiplying out and collecting like terms:

$4b(b - 9) - b(2 - b)$

$({z^2}y + {z^2} - x)(z - x)$

$(m + n)({m^2} - {n^2})$

$-5x(x+3y)^2$

$(5t + 2)(25{t^2} - 10t + 4)$

${({z^4} - 3)^2}$

$(2a{b^2} - 5{a^2}b)(21{a^5}{b^4} - 14{a^4}{b^5} + 7a{b^3} - b)$

${(2a + 3b)^3}$

$1 - (1 + [1 - (1 + y)])$

If ${x^2} + 7x + 8 = (x + 3)(x + 4) + p$ is always true, then $p = $ …

Reduce each fraction as much as you can (which may be not at all).

$\frac{{14{a^2} - 18a}}{{2a}}$

$\frac{{{x^2}y - {x^7}{y^2}}}{{{x^2}y}}$

$\frac{{ - 12m(m - 13)}}{3}$

$\frac{{4x + 2y - 3}}{2}$

$\frac{{8{x^3}{y^5} - 6{x^4}{y^3}}}{{{x^2}{y^3}}}$

$\frac{{24{r^3}{s^{ - 2}} - 36{r^{ - 1}}{s^5}}}{{{r^{ - 2}}{s^{ - 3}}}}$

. $\frac{{6{x^3} - 12x{y^{\frac{2}{3}}}}}{{{x^{\frac{1}{2}}}y}}$

$\frac{{6{f^4}g - 5{f^2}{g^3}}}{{fg}}$

$\frac{{\left( {\frac{{2x + 2}}{x}} \right)}}{{\left( {\frac{x}{{x + 1}}} \right)}}$

$\frac{{{{({n^2} - 6n + 14)}^6}}}{{{{({n^2} - 6n + 14)}^4}}}$

Add the fractions:

$\frac{8}{p} + \frac{q}{2}$

$\frac{1}{x} + \frac{3}{{{x^2}}}$

$\frac{{2y + 3}}{6} - \frac{{y + 3}}{4}$

$\frac{3}{{ab}} - \frac{4}{{{b^2}}}$

$\frac{4}{{2x - 1}} - \frac{3}{{2x}}$

$\frac{2}{{x - 1}} + \frac{2}{{x + 1}}$

$\frac{{{w^2} + 2w + 1}}{w} - \frac{{{{(w - 1)}^2}}}{w}$

What is the result when $3 - 2x$ is subtracted from the sum of $x - 3$ and $5 - x$ ?
(From Andres et al, Preparing for the SAT Mathematics. Amsco, 2005.)

If $3x - 7 = 5$ , then $9x - 21$ =…?

If ${x^2} + {y^2} = 37$ and $xy = 24$ , what is the value of ${(x - y)^2}$ ?

Prove that if one positive integer is 3 more than another, the difference in their squares must be a multiple of 3, but cannot be a multiple of 6.

Write each in the form ${a^b}$ , where $a$ and $b$ are integers not equal to 1:

${3^4}{9^5}{27^6}$

$4^5 15^{10}$

How many ${2^3}$ terms are there on the left side of the equation?

Solve for $x$:

$3{x^5} = 96$

$\frac{2}{3} \; x^3 = 22$

${x^{\frac{4}{5}}} = 37$

$6{x^{- \frac{{1}}{6}}} = 66$

$217{p^{\frac{2}{9}}} = 53$

$5\sqrt {5x - 1} = 7\sqrt {2x + 5} $

$\sqrt{3x+3} = x + \frac{3}{2}$

Rewrite in the form ${a^b}{c^d}$ , where $a$, $b$, $c$, and $d$ are each integers not equal to 1 and less than 10:
$27^{\frac{4}{3}} \cdot 216^{\frac{2}{3}} \cdot 32^{\frac{3}{5}}$

Simplify the following expressions, making sure there are no negative exponents:

$\frac{{{x^{ - \frac{2}{3}}}}}{{{x^{\frac{4}{3}}}}}$

$\frac{{{x^2}{y^{\frac{1}{4}}}}}{{{y^{ - \frac{1}{2}}}{x^{\frac{5}{3}}}}}$

$\big(\frac{16^{\frac{3}{4}} x^\frac{4}{3} y^{-2}} {121^{-\frac{1}{2}} x^{-\frac{2}{3}} y^{-3}}\big) ^3$

How many distinguishable 6 letter words can be formed from the letters of “twists”, where each letter can only be used once per word? What if the t’s and s’s were given different colors, so they could be distinguished from each other as well?

How many ways can you step right 4 times and left 7 times in a sequence of 11 steps? Put another way, how many ways can you arrange 4 R’s and 7 L’s in a straight line, where the R’s and L’s are indistinguishable from each other?

Suppose you’re going to toss a coin 8 times and record the sequence of heads and tails. How many different sequences are possible?

Josephine flips a coin 9 times. What is the probability that she’ll get exactly 6 heads? 4 heads? 3 heads?

How many ways are there to form a committee of 5 people from a class of 80? (There are at least two different methods to solve this problem)

In going packing for a trip, you and your spouse need to pack 4 ties and 6 dresses. You own 7 ties and 10 dresses. How many different ways can you select the ties and dresses for your trip?

How many ways can you select 4 letters from the word “fishbowled”, if the order of the letters selected is unimportant? What if the order is important?

If you start in the lower left corner of an 8x8 chess board, and for each “step” you can move either one square to the right or one square up, how many different ways are there to reach the upper right corner of the board?

In how many ways can five girls be chosen from a class of 20 if Sarah Dreadful has to be chosen (so that she won’t throw a fit)?

Julius goes to a yard sale and sees 8 books on sale. He thinks that he would like to buy either 2, 3, or 4 books. How many different possibilities are there for what books he could buy at the yard sale?

Ten people meet at a party, and each pair of people shake hands. How many handshakes are there?

Three identical prizes are to be given to three lucky people in a crowd of 100. In how many ways can this be done? What if the prizes were not identical?

You plan on forming a Sophomore Prom committee consisting of 8 sophomores. The Sophomore Class has 45 boys and 35 girls in it. How many distinct committees can be formed if

there are no restrictions placed on the committee other than there must be 8 sophomores on the committee?

there are to be 4 girls and 4 boys on the committee?

the committee cannot have Sarah Dreadful on it?

A boat has 3 red, 3 blue, and 2 yellow flags with which to signal other boats. All 8 flags are flown in various sequences (1 flag at a time) to denote different messages. How many such sequences are possible?

Five boys and five girls stand in a line. How many different arrangements are
possible:

If boys and girls can be intermixed (or not) in the line?

If all the boys stand at the back of the line?

Henry’s Hamburger Heaven offers its hamburgers with the following condiments: ketchup, mustard, mayonnaise, tomato, lettuce, pickles, cheese, and onions. A customer can choose one, two, or three meat patties, and any collection of condiments. How many different kinds of hamburgers can be ordered?

A “necklace” is a circular string with several beads on it. Two necklaces are the same if they are just rotations, in the plane, of each other. How many different necklaces can be made with 10 different beads?

How many 6-digit numbers have at least one even digit?

There are five books on a shelf. How many ways are there to arrange some or all of them in a stack? The stack may consist of one book.

The map of a town is depicted below. Ian lives at point I; the library is at point L; and the grocery store is at point G. Ian can only walk south or east. The town is many times bigger than the map.

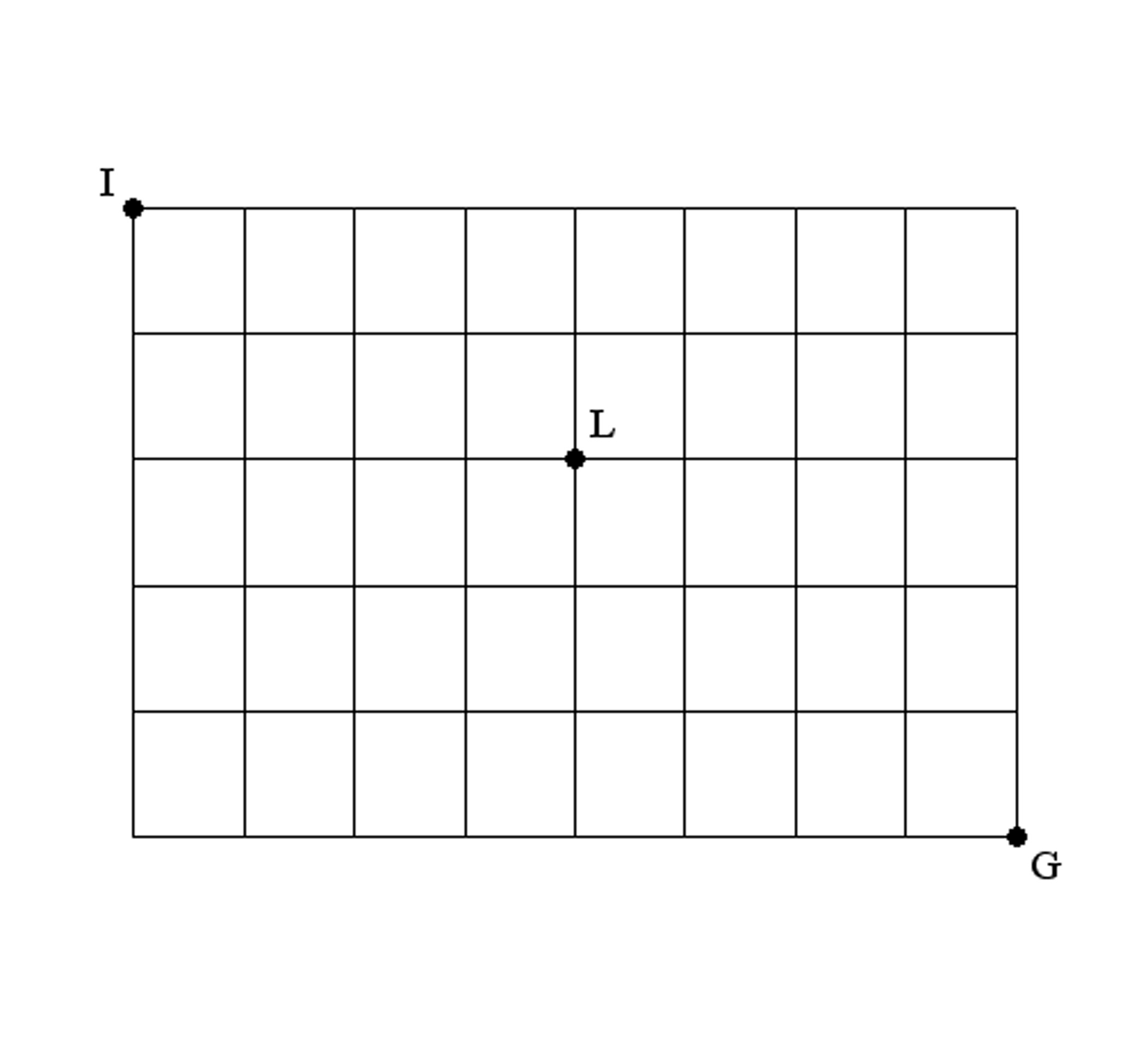
How many different ways are there for Ian to walk from his house to the library?

How many different ways are there for Ian to walk from the library to the grocery store?

If Ian wants to walk from his house to the grocery store by way of the library, how many different ways can he do this?

Suppose Ian uses a coin flip to decide whether he’s going to go one block south or one block east. After he walks a block, he then tosses the coin again and follows the previous guidelines regarding his movement. If it takes Ian one minute to walk one block, then what is the probability that he will make it from his house to the grocery store in 13 minutes? Assume it takes him no time to flip the coin and interpret the meaning of the outcome.

One student has 6 novels and another has 7 novels. How many ways are there for the first student to exchange 3 novels with 3 novels owned by the second student?

How many 5 digit numbers have factors of 4 or 5?

The equation below shows a series of 1’s summing to 14.

$1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 14$

How many ways can you choose 3 of the plus signs to circle?

Clearly explain how your answer to Part a also answers the question below.

How many solutions are there of the equation $x + y + z + w = 14$ in positive integers? Note: the solution $\left( {1,2,8,3} \right)$ is different from the solution $\left( {2,3,1,8} \right)$.

What is the probability of getting 5 heads out of 10 tosses of a fair coin?

Suppose you draw at random 5 cards from a standard 52-card deck.

How many possible different 5-card hands are there?

How many ways can you pull 5 cards such that you get exactly one ace?

How many ways can you pull 5 cards such that you get exactly two aces?

How many ways can you pull 5 cards such that you get exactly two aces and three kings?

What’s the probability of pulling 4-of-a-kind?

Suppose you are standing at zero on the real number line. You toss a fair coin and move 1 unit to the left if you get heads. You move one unit to the right if you get tails. You do this 17 more times for a total of 18 coin tosses.

After 18 tosses what are the possible numbers you might be at on the real number line?

What is the probability that you will be standing at 0 after 18 tosses? At -2? at -3?

For fun on a Friday night you and a friend are going to flip a fair coin 10 times. Let H represent the outcome that a flip shows heads and T represent tails. Assume that ${\rm{Prob}}\left( {\rm{H}} \right) = {\rm{Prob}}\left( {\rm{T}} \right) = 0.5$ .

You flip the coin 10 times and get the sequence HTHHHTTHHT. Your friend does likewise and gets HHHHHHHTTT. Which of these two sequences was more likely to occur? Justify your response.

What is the probability that you will get at least two heads in 10 tosses of the coin?

The numbers 1, 2, 3, …, 25 are placed in random order. What’s the probability that the numbers 1, 2, 3 are next to each other?

a. Suppose that 14 people are arranged randomly in a line and two of these people are Emma and Eric. What’s the probability that there are 3 people standing between Emma and Eric?

Suppose that the 14 people in Part a are arranged in a circle. What’s the probability that there are 3 people standing between Emma and Eric?

Suppose you will roll a standard, fair six-sided die until you get a 2. What’s the probability that you will stop rolling after the first roll? What’s the probability that you will stop after the second roll? What’s the probability that you will stop after n rolls?

Eight first graders, 4 girls and 4 boys, arrange themselves at random around a merry-go-round. What is the probability that boys and girls will be seated alternately?

Rick writes letters to 8 different people and addresses 8 envelopes with the people’s addresses. He randomly puts the letters in the envelopes. What is the probability that he gets exactly 6 letters in the correct envelopes? What about 7 letters?

There are 40 people waiting to be selected for a 12-person jury. Of the forty, 20 are African-American, 15 are Hispanic, and 5 are Caucasian.

How many different 12-person juries (called “jury panels”) can be picked from this group of 40? Show your work.

How many jury panels can be picked that have only African-Americans? Show your work.

Show that the probability that an all African-American panel would be picked just by chance is approximately .0000225. Show your work.

If you were a judge and the two lawyers working a case in your court picked an all African-American jury panel (or a jury panel with no African Americans on it) from the pool of 40 given in the beginning of this problem, would you believe that this panel was created without consideration of race? Explain, making direct reference to the probability in Part c.

Suppose Tony’s class is trying to form two committees — the Social Committee and the Fund Raising Committee — from the fourteen students in his class. How many possible arrangements are there of the fourteen students into these two committees, if each student is allowed to choose one committee or neither to be on? Show your work.