Introduction
You have already seen how coordinate geometry works, with the focus on slope and distance. Now you will be considering an earlier geometry, where there are no coordinates, so lines don’t have particular slopes, nor do we determine numerical distances between points. It’s just our reasoning and imagination that enable us to discover valuable relationships among the figures we draw.
In this lesson, you will start to use this reasoning and imagination to help uncover the structure of geometry. Some things you know about geometry are simple and you may be happy to take them on faith. Others are less obvious, but can be explained by a careful argument. Still others may remain mysterious for now.
To give you some tools, let’s start with the figure below, which you have probably seen in various contexts. The figure shows parallel lines a and b and line t crossing them. The line t is called a transversal, as it “moves” across the other pair of lines.

In the figure above, label all the acute angles you believe to be equal in measure with the letter $x$. Then label all the obtuse angles you believe to be equal in measure with the letter $y$. Are there any angles that you haven’t labeled?
What is the relationship between the value of $x$ and the value of $y$? Make an argument that doesn’t depend on knowing the specific value of $x$ or of $y$.
Some of these pairs of angles come up often enough so as to deserve special mention. In the diagram below angles 1 and 3 are corresponding angles. Angles 3 and 7 are alternate interior angles. Angles 2 and 3 are same-side interior angles. Notice that lines $l$ and $m$ need not be parallel, yet the names still apply.

Name another pair of angles in the above figure that are
Corresponding.
Alternate interior.
Same-side interior.
In the figure showing lines $l$ and $m$ not parallel, you’ll notice that there are no longer so many pairs of equal angles. But there is a fact that carries over from the previous figure. What is it, and how do you know for sure?
If you have two parallel lines crossed by a transversal, do you think that the pairs of corresponding angles will always be equal? How about the pairs of alternate interior angles? Try to find an exception.
Draw another two parallel lines crossed by a transversal. The same-side interior angles probably don’t look equal. Is there anything else you can say about them? If you’re not sure, take some measurements.
Development
The results you found/reviewed in the introduction are basic results in geometry. You may have learned them before, and you may consider them so obvious that you wonder why anyone would point them out. The reason is that we can use those simple facts to convince ourselves of some results that are not so simple!
For instance, you have probably been raised to believe that there are 180 degrees in a triangle, even though that fact is not visually obvious. But the few results we’ve stated so far in this chapter can serve to convince us once and for all.
Below is a triangle, meant to be general enough to stand for any triangle. It would be nice to use some of your findings so far to prove that the sum of its angles is 180 degrees. However, there are no parallel lines in this picture, so there doesn’t appear to be much we can do.

Add something to the diagram so that you do have some parallel lines.
Now that you have some parallel lines, label as many angles as you can that you know to be equal.
Now finish the proof that the angles of a triangle add up to 180 degrees.
You have probably known for a long time that the angles of a triangle add up to 180 degrees — in that sense, you did not learn any new facts by doing this proof. However, you may not have realized how strongly the result depends on alternate interior angles (or whichever angle pair you decided to use) being equal when lines are parallel. In fact, there are non-Euclidean geometries in which the alternate interior result is not true, where the alternate interior angles result is not true — and, sure enough, in those geometries, the angles of a triangle can actually add up to more or less than 180 degrees!
The ancient Greeks appreciated how important it was to uncover the structure of geometry, and very often looked for proofs of statements they were pretty sure were true using statements they already knew to be true. They tried to reduce the number of statements they accepted without proof to the smallest number possible. The most famous Greek geometer, Euclid, was able to reduce his number of assumptions to five mathematical statements and five “common notions” — like “two things equal to the same thing are equal to each other.” He was able to prove a huge amount of geometry from these simple assumptions.
In the spirit of Euclid, try to prove that angles 1 and 3 below are equal. What facts are you relying on?

The rest of this Development consists of examples of some other argument styles that do not involve coordinates.
Another fact you have known for a long time is that the area of a triangle can be found by the formula $\text{Area } = \frac12 \cdot \text{base} \cdot \text{height}$. You might also have seen the following picture, designed to show why the formula is true for right triangles.
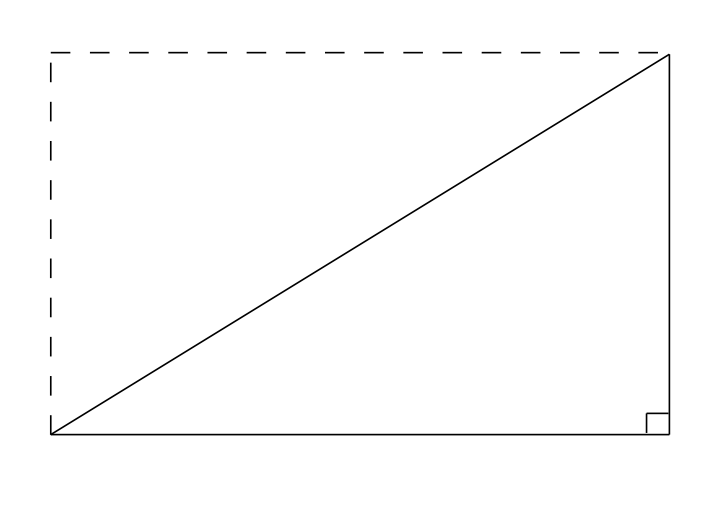
But alas, not all triangles are right, and we’d still like to be able to use this familiar formula with any triangle. So below is triangle $ANY$.

Add something to the diagram so that you can use what you know about the area of rectangles and right triangles to find its area. Is your formula equivalent to $\text{Area } = \frac12 \cdot \text{base} \cdot \text{height}$?
And last, but not least, a Physical Challenge:
Using only a compass and a tool for drawing straight lines, construct an equilateral triangle. Your tool for drawing straight lines may not be a ruler, or anything else that can take measurements.
Come up with an argument that would convince a friend that the triangle you constructed really has to be equilateral and, if they did the same thing, their triangle would be equilateral, too.
Practice
Given that $\overline {AB} $ is parallel to $\overline {CD} $, which pairs of angles must be equal?

In the figure below, ABCD and PBQD are parallelograms. Which of the numbered angles must be the same size as the angle numbered 1? (Copyright Phillips Exeter Academy)

Given the following figure, where only the horizontal segments are parallel, name three angle pairs that are equal and three angle pairs you can conclude are supplementary: that is, sum to $180^\circ$.

Assuming that alternate interior angles are equal when lines are parallel, prove that corresponding angles must be as well.
In problem 11, triangle $ANY$ was meant to stand for any triangle, but notice that triangle ANY was drawn to be acute. Try the argument again with an obtuse triangle, and see if you can still obtain the formula $\text{Area } = \frac12 \cdot \text{base} \cdot \text{height}$.
The two line segments below are “half” of a parallelogram. Trace it into your notebook. Then use a compass and straightedge to draw in the remaining two line segments. How do you know for sure that what you’ve got is a parallelogram?
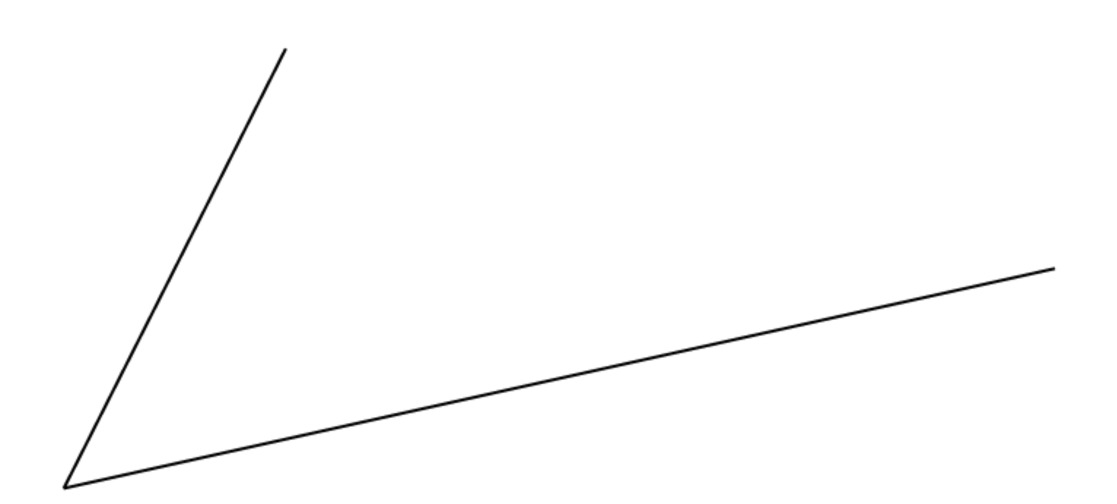
In the figure below, the angle $d$ is an exterior angle of this triangle. Determine experimentally if there is any relationship between d and the measure of any angles of the triangle. Does your observation apply even for an obtuse triangle (a triangle where one angle is greater than 90 degrees)?

Prove the result you found in the previous problem.
Problems
Now that you’ve proved that the sum of the measures of the interior angles of any triangle is ${180^ \circ }$, experiment with the sum of the measures of the interior angles of any quadrilateral. How about other polygons? Prove what you find.
How many regular polygons have interior angles that are integers? How can you be sure your answer is correct?
On the bus, Rafael asked his three friends what they had figured out for the sum of the interior angles of a 500-sided polygon. Lemuel said he got 8640. Julia got 89640, and Marla got 899640. Rafael didn’t have any of his books, pencil, or paper, but he was still able to determine who was likely to be right. Can you?
You know the sum of the interior angles of a triangle, but how about the sum of the exterior angles of any triangle? (see the figure below — the exterior angles are $d$, $e$, and $f$.) Take measurements, if necessary, and then try to prove what you found.

What do you suppose would be the sum of the exterior angles of a quadrilateral? Try it out on some different quadrilaterals. See if you can prove it.
Draw any triangle $ANY$. Recall that a median is a line segment from a vertex of a triangle to the midpoint of the opposite side. A median will split a triangle into two smaller triangles. Try this with a few different triangles. Try to draw a triangle so that the left triangle created by the median visibly has a larger area than the right.
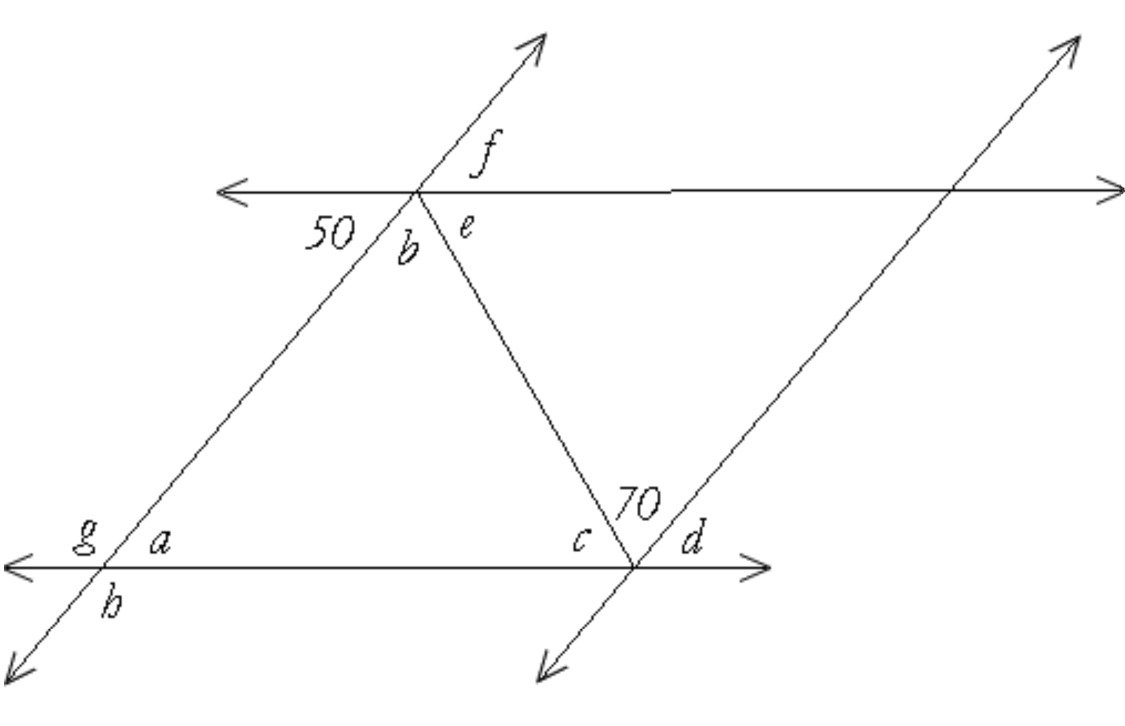
Given the following figure, where both pairs of lines that appear parallel are assumed parallel, find all the angles represented by letters.
Try to prove or disprove the statement “If two lines intersect the same line, they must intersect each other.”
Here is a triangle. Using only a compass and straightedge, make an exact copy of the triangle in your notebook. No tracing allowed.

You know from the beginning of the chapter that, if lines are parallel, then alternate interior angles created by a transversal are equal. So, does this imply that in the figure below, must lines $a$ and $b$ be parallel?

Though it seems obvious, one of Euclid’s theorems was “If two lines are parallel to a third line, they are parallel to each other.” Prove this statement. Remember the tools you have to prove that lines are parallel.
In the figure below, (which means the measure of angle BCA equals the measure of angle FDE). Also, the points $A$, $C$, $D$, and $F$ all lie on a straight line. Is this enough evidence to claim that $\overline {BC} $ must be parallel to$\overline {DE} $? Explain.

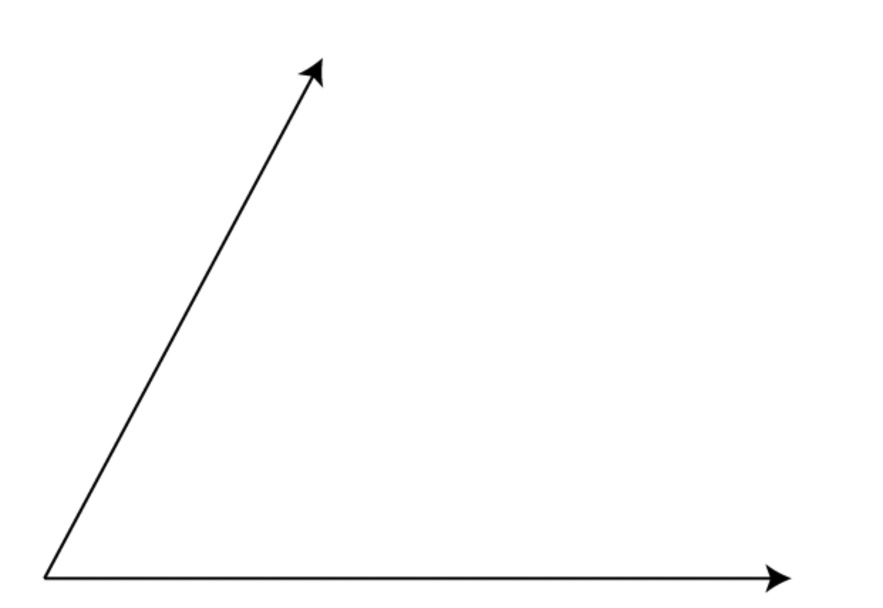
Here is an angle. Using only a compass and straightedge, find a way to copy the angle into your notebook. (Again, no tracing allowed.)
Would you claim that $l$ and $m$ are parallel in the following figure? Explain.
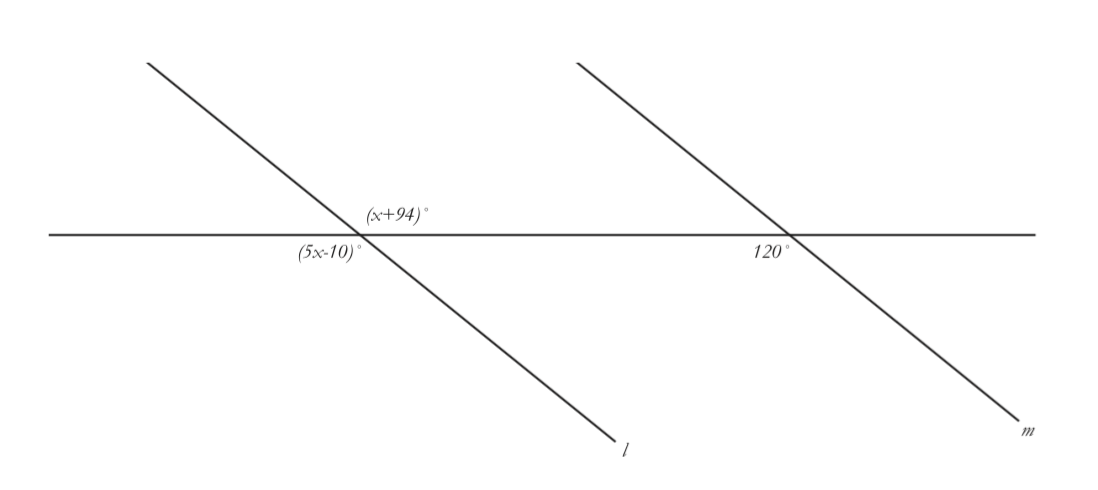
In the figure below, what would $x$ need to equal if you could claim correctly that $l$ and $m$ are parallel? Explain.

If $p$ and $q$ are parallel, find $y$.

If $m$ is not parallel to $n$, what can’t $x$ equal?

The shorter side of a rectangle is 10 units. If the diagonal is two units more than the longer side of the rectangle, what is the area of the triangles created by the diagonal?
If $a$ is parallel to $b$, find $x$. (Hint: this is a problem for which geometric tinkering will prove useful.)

Assume line $p$ is parallel to line $q$. You are given that $m\angle 2 = x + 15$, and $m\angle 3 = 10y + 40$. Find $m\angle 2$.

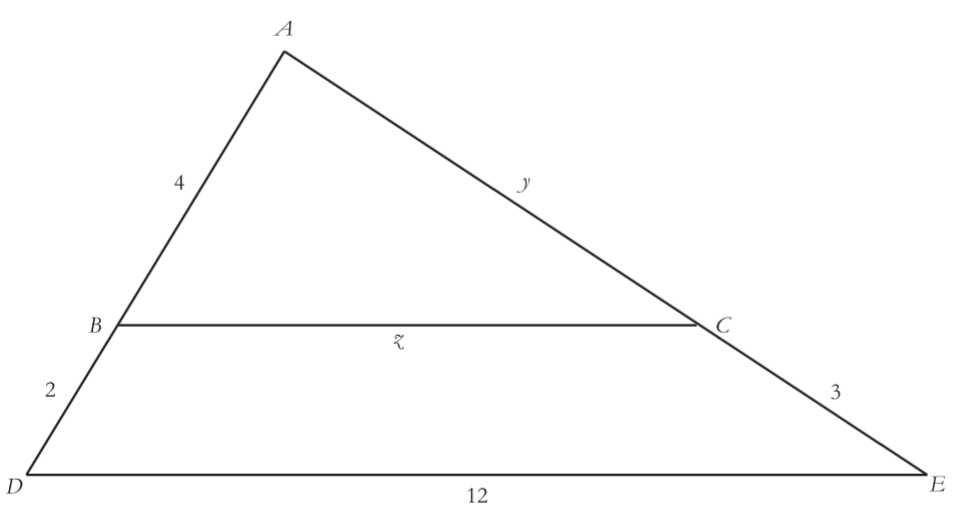
Given that $\overline {BC} $ is parallel to $\overline {DE}$, what can you conclude about triangles ABC and ADE? What would be the length of$\overline {AC} $? $\overline {BC} $?
Don’t use a calculator for this problem.
Simplify $\sqrt {\frac{3}{4}} $
Simplify $y^2-\left(\frac12 y\right)^2$
Factor ${x^2} + 3x + 2$
Reduce the fraction $\frac{x^2-8x+16}{x^2-11x+28}$
What value of $x$ satisfies ${2^5} + {2^5} + {2^5} + {2^5} = {2^x}$?
There are a number of other two-dimensional forms that we can find the areas of now that we know the area formulas for rectangles and triangles. Here are some.
Draw a triangle $ANY$ and a line parallel to $\overline {AY} $ so that it cuts through the sides $\overline {AN} $ and $\overline {NY} $. Let $\overline {BC} $ represent the parallel line intersecting the triangle. Now erase what’s above $\overline {BC} $. You’re looking at what is called a trapezoid — a four-sided figure with one pair of parallel sides.
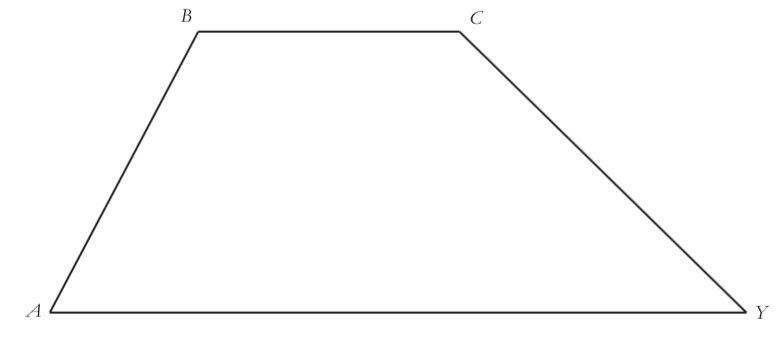
Knowing what you do about the areas of triangles and rectangles, come up with a formula for the area of a trapezoid. You may want to label $BC$, the top base, as ${b_1}$ and $AY$, the bottom base, as ${b_2}$. What other dimensions of the trapezoid might be useful?
If we now consider any parallelogram $ABCD$, not just those with right angles, we can consider whether there is a unique formula for the area of any and all parallelograms, including rectangles and squares.

Partition the parallelogram (divide it up) into shapes that you already know the area of. By summing the areas of these shapes, find an area formula that should work for any parallelogram.
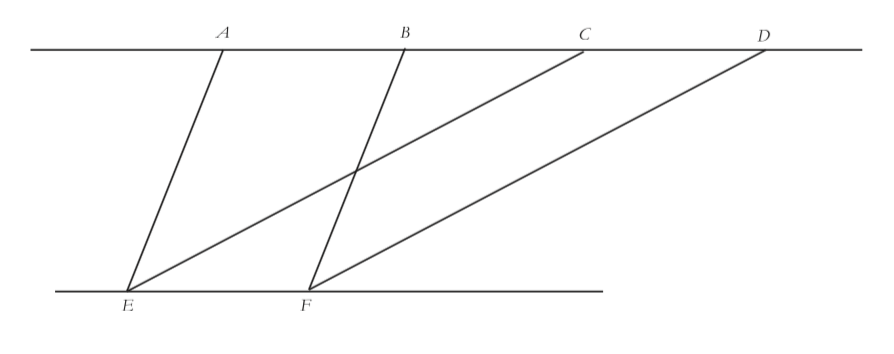
Given the image below where it is assumed the horizontal segments are parallel, what can you conclude, if anything, regarding the areas of parallelograms $ABFE$ and $CDFE$?
If the lengths of the sides of a parallelogram are doubled, what seems plausible regarding the area of the new parallelogram? Can you make an argument that your conjecture is the case?
A certain trapezoid has bases of length 10 and 24, sides of length 13 and 15, and a height of 12. If you were to make an enlarged, scale copy of the trapezoid whose area was 4 times that of the original, then what would the measurements of the larger trapezoid be?
Let $ABCD$ be a square, and $EFGH$ another square whose area is twice that of square $ABCD$. Prove that the ratio of $AB$ to $AC$ is equal to the ratio of $AB$ to $EF$.
The ancients who studied form naturally included others besides the Greeks. There were the Egyptians who designed and built pyramids and came up with a very interesting formula for the area of a circle (see if you can find it on Google and see what an impressive fit it provides). The Babylonians also studied form, and they came up with a formula for the area of a quadrilateral.
The Babylonians’ formula for the area of a quadrilateral is ${\rm{Area = }}\frac{{(a + b)(c + d)}}{4}$, where $a$ and $c$ are the lengths of one pair of opposite sides of a quadrilateral, and $b$ and $d$ are the other. Does their formula always, sometimes, or never work? (Try this with quadrilaterals you actually know the area of.)
Exploring in Depth
Earlier in this lesson, you probably decided that, if you have lines crossed by a transversal in such a way that the alternate interior angles created are equal, then those lines must be parallel. Here’s a suggestion for arguing that your conjecture must be the case. Suppose that you had alternate interior angles that were equal, but the lines were NOT parallel. Do some geometric tinkering to derive some interesting things.
If $BCDE$, $FEHI$, and ACGI are rectangles, can you logically conclude that quadrilaterals $ABEF$ and $EDGH$ have the same area?

The polygons you have studied in this unit have mostly been convex. When you pick any two points inside a convex polygon and connect them with a straight line segment, the line segment always stays within the polygon. If there are two points where the line connecting them must go outside the polygon, then the polygon is called nonconvex.
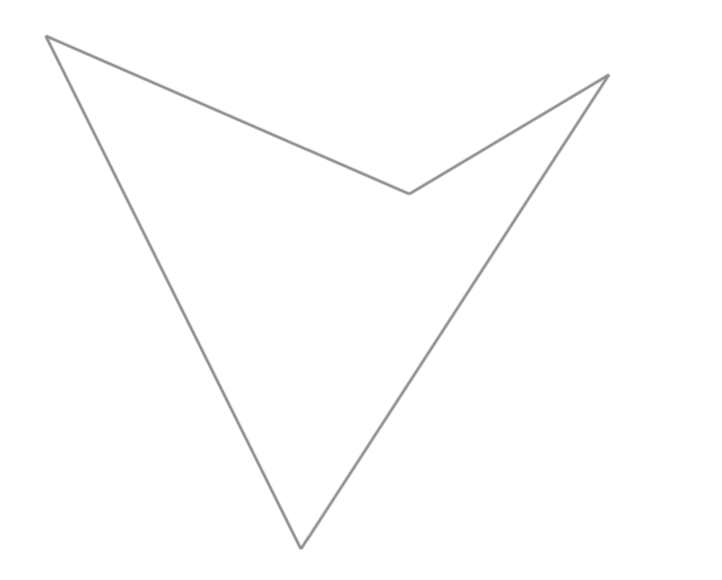
Show that the polygon above is nonconvex.
Draw in the exterior angles of this polygon. See Problem 24 if you need a reminder.
Do the exterior angles of a nonconvex polygon still add up to 360 degrees? Experiment.
First remind yourself of the result in problem #31. Then consider the following image. As you have seen in Euclidean geometry parallel lines are infinite lines in the same plane that don’t intersect. Given the circle as the entire universe, lines $AB$ and $DE$ are said to be parallel, as are lines $AC$ and $DE$, as neither pair has any intersection points within the circle. However, lines $AB$ and $AC$ are not parallel. How does this finding fit with your finding in problem 31?

Draw a good-sized equilateral triangle and pick any point inside the triangle. From that point draw the three perpendiculars to the three sides of the triangle. Let the lengths of the three perpendiculars be $a$, $b$, and $c$. If $d =$ height or altitude of the triangle, show that $a + b + c = d$. (Quite a surprise?)
Draw a right triangle. On each of the three sides of the triangle draw equilateral triangles where the side of the original triangle is also a side of the new triangle. Each of those equilateral triangles has an area. Does it seem that the sum of the areas of the equilateral triangles on the legs of the right triangle is equal to the area of the equilateral triangle on the hypotenuse? Can you prove this? (Hint: what do you know about 30°-60°-90° triangles?)

Draw any line segment on a piece of paper. Now come up with a compass-and-straightedge construction to bisect the segment — cut it exactly in half.