Introduction
C’est Mathematique! is a French expression meaning that something is so certain, it is definite. Indeed, the 19th-Century French mathematician Pierre-Simon Laplace imagined a demon that could predict every future event because it knew the exact position of every particle in the universe, and the mathematical laws that governed the motion of those particles.
Though no such demon exists, we can see why Laplace might have imagined one. Our mathematical knowledge does seem more certain than some other facts we believe to be true about politics or human nature. For instance, maybe you think that passing laws to ban handguns will reduce homicides. Then you read a study that says that actually these bans don’t have that effect. You might change your mind about whether banning handguns is a good idea… until you read another study that says that the bans do reduce accidental death among children. You’ll always have to remain open to changing your opinion based on new information.
Likewise, in the history of science, people once thought that the atom was the smallest particle that existed (the word “atom” comes from a Greek word meaning “indivisible”). Now we know that atoms are made up of protons and neutrons, and in recent decades scientists have discovered quarks. In the scientific community, people are constantly revising and improving accepted theories.
In mathematics, on the other hand, we still accept the results of ancient texts. Archimedes, Pythagoras, and Euclid are credited with many of the results that we still use today. You have probably already proven things mathematically in such a way that you’re sure they must be true. In this lesson we’ll look at what it means for a proof to be absolutely airtight — with no possibility you’ll want to revise your opinion later.
Development
Let’s think about the following two statements:
The diagonals of a parallelogram bisect each other.
The diagonals of a parallelogram bisect the angles from which they’re drawn.
Make some sketches to determine whether you think each of these statements is true or false. Recall that “bisect” means “cut exactly in half.”
When we do proofs in this section, we’re going to focus on making them airtight. We’ll use the following standard. Any time we make a statement as part of a proof, we need to be able to give a reason for that statement. That reason, in turn, needs to be a statement about geometry that we $already$ know to be true.
Here are some statements about geometry you already know to be true:
- In an isosceles triangle, the angles opposite the congruent
sides are
congruent.
- When parallel lines are cut by a transversal, same-side
interior angles
add up to 180 degrees.
- Vertical angles are equal.
- If two sides and the angle between them in one triangle are
congruent to two sides and the angle between them in another
triangle, then the triangles are congruent. (SAS congruence
theorem)
- If the three sides of one triangle are all related to the sides
of another
triangle by the same proportion, then the triangles are
similar.
(SSS similarity theorem)
- In a parallelogram, opposite sides are congruent.
Make a list of statements about geometry that you know to be true, including the six statements above. To get ideas, try paging through your notes from the past few weeks, or through the lessons earlier in this textbook. Which results seem worth remembering? Also think about some basic shapes you know, like quadrilaterals, and write down some facts you know to be true about each one.
As you may recall from the first lesson of this chapter, the Greek mathematician Euclid did something very similar to what you are about to do. He boiled down his geometric knowledge to a few assumptions and then proved the rest of what he knew about geometry using those few things. He called the facts he assumed without proof “postulates.” Any fact that he had proved was a “theorem.”
Consolidate the list you made in the previous problem with the rest of the class. Discuss which items on it are postulates and which are theorems. Now separate a blank page of your notebook into two columns. Label one column “postulates” and the other “theorems.” Write the items in the class list in the appropriate column. Leave yourself lots of room in both columns to add to the list, probably over multiple pages.
Hang on to this list. You’ll be referring to it for the remainder of this chapter.
Now let’s return to the problem of proving the statements from the beginning of this lesson. If you did your job carefully, you’ll have found that the first statement was true — the diagonals of a parallelogram bisect each other.
Before writing our airtight proof of this fact, it’s important to know where to start. Since we’re proving something about a parallelogram, it’s all right to assume that we $have$ a parallelogram. So let’s draw one…
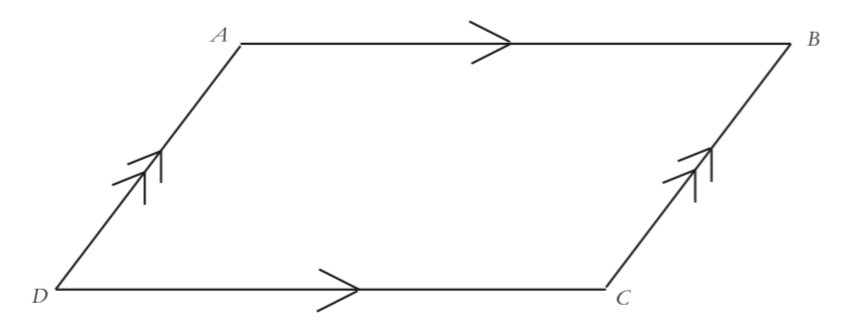
… and label the vertices so that we can talk about them later. So, specifically, $\overline {AD} \parallel \overline {BC} $ and $\overline {AB} \parallel \overline {DC} $. Those are two things we know for sure. It’s also important to be sure of what we want to show about this diagram. Let’s draw in some diagonals and call their intersection point $E$.

Then what we want to show is that $\overline {AE} \cong \overline {EC} $ and $\overline {BE} \cong \overline {ED} $.
The comic book hero G.I. Joe used to say “knowing is half the battle.” In the case of proof, knowing what information you have to start with and where you want to end up with is half the battle. Really!
What we need now is a chain of reasoning, beginning with the facts that $\overline {AD} {\kern 1pt} {\kern 1pt} \left\| {{\kern 1pt} {\kern 1pt} \overline {BC} } \right.$ and $\overline {AB} \parallel \overline {DC} $ and ending with the statement that $\overline {AE} \cong \overline {EC} $ and $\overline {BE} \cong \overline {ED} $. In this chain of reasoning, every step needs to be justified with some reason we know for sure.
Try this yourself before reading the proof on the next page.
When thinking about what will help us to write this proof, let’s think backwards a little bit. We want to show that certain lengths are the same. Look back at your list of postulates. What tools do you have for showing that lengths are the same? Not the results about parallel lines. Not vertical angles or linear pairs. Possibly some statements you have about parallelograms or rhombuses, but in this case the lengths we’re interested in are diagonals rather than sides of those shapes. That really only leaves one thing that could help — congruent triangles.
If we can show that certain triangles are congruent, then we can conclude that the lengths making them up are also congruent. That should be our strategy in writing this proof.
Find some congruent triangles in this diagram that you think would help. Do you know for sure they’re congruent?
Depending on the way you answered question #5, you may have an airtight proof already. Let’s write one out as an example of a chain of reasoning in which all the steps are justified.

- Given: $\overline {AD} \parallel \overline {BC} $ and $\overline {AB} \parallel \overline {DC} $.
- Goal: Prove that $\overline {AE} \cong \overline {EC} $ and $\overline {BE} \cong \overline {ED} $.
- $\angle DAE \cong \angle BCE$ because they are alternate
interior angles of
the parallel lines $\overline {AD} $ and $\overline {BC} $.
- $\angle ADE \cong \angle CBE$ for the same reason.
- $\overline {AD} \cong \overline {BC} $ because opposite
sides of a parallelogram are congruent.
- Therefore, $\triangle AED \cong \triangle CEB$ by the
ASA congruence theorem.
- $\overline {AE} \cong \overline {EC} $ because they are
corresponding parts of congruent triangles.
- $\overline {BE} \cong \overline {ED} $ for the same
reason.
Are we done? YES! We’ve accomplished our goal, showing that the diagonals cut each other in half.
That proof might have been written with a little more care than you are used to. Your class will have to decide exactly how much writing is expected in a proof. But notice that every step in the argument comes from your list of postulates, so that anyone who accepts the postulates can't disagree with your conclusion — there is no “wiggle room” in this proof.
Meanwhile, you should have found that it is not true that the diagonals of a parallelogram bisect the angles. You may remember from last year that an example designed to show that something isn’t true is called a counterexample. Here’s what a counterexample to this statement might look like:

You can see from this picture that it doesn’t look true that the angles are bisected, and so it isn’t worth your time to look for a proof.
In order to start the proof that the diagonals of a parallelogram bisect each other, we had to know exactly what the word “parallelogram” meant. That’s how we knew to start with the statements “$\overline {AB} {\kern 1pt} {\kern 1pt} \left\| {{\kern 1pt} {\kern 1pt} \overline {CD} } \right.$ and $\overline {AD} \parallel \overline {BC} $”. Whenever we write a proof, we’ll have to be very precise about what we mean by the objects we’re talking about. For instance, last year you worked with the definition of a square: a quadrilateral with four congruent sides and four right angles.
Come up with a definition for each shape. Then compare notes with your class if you haven’t already done so.
A rectangle
A parallelogram
A rhombus
A trapezoid
A kite
A circle
Now begin a section in your notebook labeled “definitions,” again leaving space for you to add definitions as you consider new shapes. Start with the definitions you came up with in Problem 6.
Considering the shapes in the previous question might remind you of some more things you know to be true about geometry. Add them to your list of postulates and theorems (which should they be?), and confer again with your classmates.
Much as you can use congruent triangles to prove things about diagrams, you can also use similar triangles.
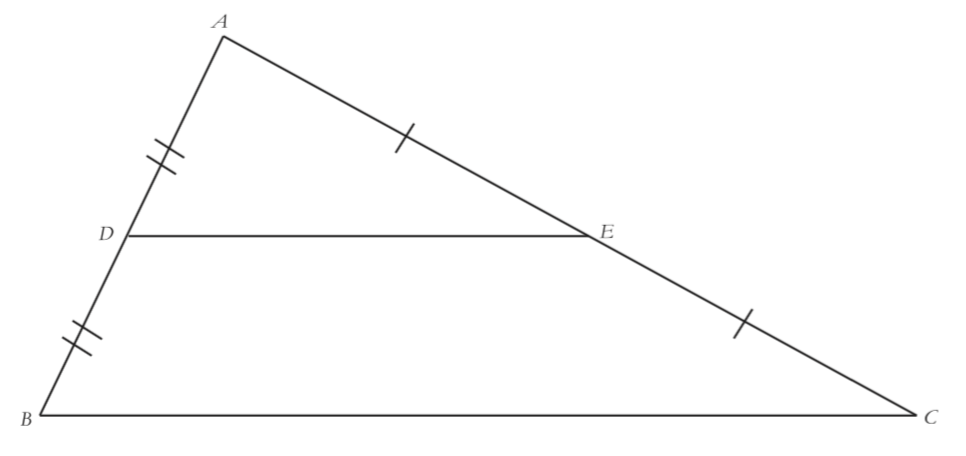
The diagram has been marked and labeled for you.
Based on the diagram, write what is given.
Can you remember the two things you showed about $\overline {DE} $ and $\overline {BC} $ last year? If not, try drawing this diagram with triangles of a few different shapes, and take some measurements in order to make a conjecture.
With an eye towards proving these results, prove that there are similar triangles in this picture (The three similarity theorems are AA, SSS, and SAS). What is the scale factor?
Finish proving what you wrote in part b about $\overline {BC} $ and $\overline {DE} $.
You’ve proven a couple of new things so far in this lesson. The interesting thing is, not only do you know those things, but you have proofs of them. Write the new things you know under the column labeled “theorems” on your list. Whenever you prove something new that you think may come in handy later, or that you just think is interesting or important, add it to this theorem list.
By the way, is there anything under “postulates” that you could prove and make a theorem?
Practice
In this problem, you will prove that the diagonals of a rectangle are congruent.
Draw a rectangle that can stand for any rectangle and label the vertices.
In terms of your diagram, write what is given and what is to be proved.
Finish the proof.
In the following five problems, you should mark up the diagram with the starting information before you attempt a proof.
Given: $\overline {AB} \cong \overline {EF} $, $\angle A \cong \angle E$, $\angle C \cong \angle D$
Prove: $\overline {BC} \cong \overline {DF} $

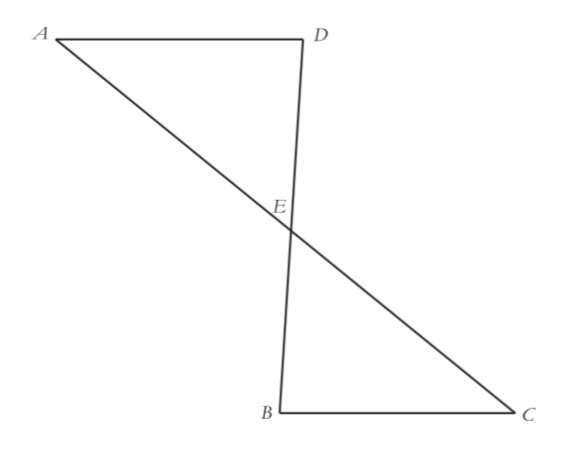
Given: $\overline {AE} \cong \overline {CE} $, $\overline {BE} \cong \overline {ED} $
Prove: $\overline {AD} {\kern 1pt} {\kern 1pt} \left\| {{\kern 1pt} {\kern 1pt} \overline {BC} } \right.$
(In this problem and in the remaining problems in this lesson, assume that lines that appear to be straight in a figure really are straight.)
There is a joke about a mathematician asked to describe an algorithm for boiling an egg. She responds, “you take a pot, fill it with water, put in an egg, put the pot on the burner, turn the burner on, and wait 20 minutes.” “All right,” you say, but what if the pot is already sitting on the burner, filled with water?” “Then,” she says, “you take the pot off the burner and empty the water, and then you’ve reduced the problem to the previous case.”
Suppose, in the diagram below, that
$\overline {PA} \cong \overline {RK} $, $\angle A \cong
\angle K$
Prove: The length of $\overline {KA} $ is twice the length of
$\overline {KS} $.
Now suppose instead that
$\overline {PA} \cong \overline {RK} $, $\overline {PA}
{\kern 1pt} {\kern 1pt} \left\| {{\kern 1pt} {\kern 1pt}
\overline {KR} } \right.$

Given: the angles and sides as marked; W, A, and T are points on a line segment.
Prove: $m \angle T = 50^\circ$

Given: $TI = 3NI$, $RI = 3AI$
Prove: $\overline {TR} {\kern 1pt} {\kern 1pt} \left\| {{\kern 1pt} {\kern 1pt} \overline {NA} } \right.$ and $TR = 3NA$

Which of these statements appear true, and which are false? If they are true, you don’t need to prove them, but if you think they are false you should provide a counterexample.
If one isosceles triangle has side lengths of 5 cm and 5 cm, and so does another, then those triangles are congruent.
In an obtuse triangle, label the longest side c and the other two sides a and b. Then ${a^2} + {b^2} < {c^2}$.
The three medians of a triangle always cross in a single point.
If someone tells you three positive integer lengths, you will always be able to draw a triangle that has those lengths.
For each figure, determine as many missing sides and angles as you can. (You don’t need to write a formal proof of your answers.) You will not be able to find $all$ of the sides and angles. Avoid using trigonometry.
In the diagram below, lines that appear parallel are parallel. Find the length of the line segment .

Going Further: Longer Proofs; Pitfalls When Writing Proofs
Sometimes the only way you can see that a statement must be true is to talk yourself through a series of steps in proof-like form. It would be hard to come to know the statement to be proven below, in any other way. In addition, the statement’s proof deals with some complications that you will sometimes come across.
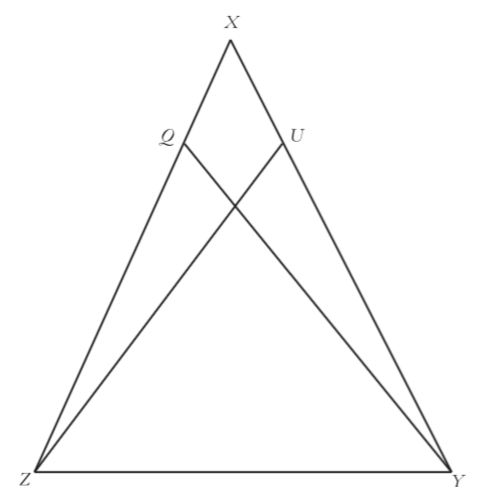
Given: $\overline {XQ} {\kern 1pt} \cong \overline {XU} $ and$\angle XQY \cong \angle XUZ$.
Prove:$\angle UZY \cong \angle QYZ$.
“Working backwards and forwards” will be very important in the planning stages of this proof. At first glance, it seems that we should try to prove triangles $QYZ$ and $UZY$ congruent, since those are the triangles that contain the two angles we want to prove congruent.
Find as much evidence as you can that $\triangle QYZ \cong \triangle UZY$.
In the previous problem you should have found a (shared) side and an angle, which by themselves are not enough to prove the triangles congruent. So we need to find another strategy. It may be that, using some other pair of congruent triangles in the figure, we can find that third piece of information needed to prove $\triangle QYZ \cong \triangle UZY$. Or, perhaps the solution is something completely different. Instead of doing all of our planning backwards, let’s return to thinking forwards and just look for any pair of triangles that might be congruent.
Name some other pairs of triangles that might be congruent in the figure. Try to find enough evidence for their congruence.
The triangles that we can actually prove congruent may have been hard to spot. As a hint, they share angle $X$. If you haven’t already, prove that these two triangles are congruent.
Now that we have congruent triangles, we can mark all of their sides and angles congruent, as follows:
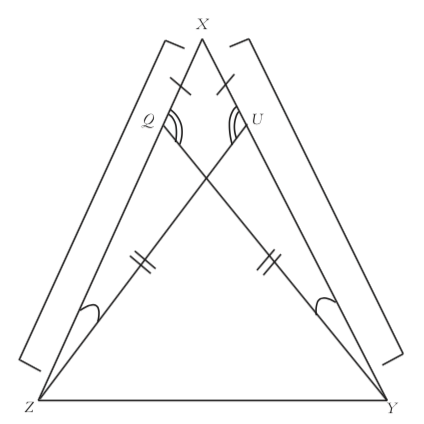
Now we can return to the question of how to prove$\angle UZY \cong \angle QYZ$. Using the information we’ve derived, argue that these angles are congruent.
One way to complete the proof is to notice that, since we now know $\triangle XYZ$ is isosceles, $\angle XZY \cong \angle XYZ$. Since these angles are both composed of two parts, and the parts $\angle XZU$ and$\angle XYQ$ are congruent to each other, that means the remaining parts must be equal as well. In other words, $\angle UZY \cong \angle QYZ$! Though this kind of part/whole reasoning doesn’t appeal to theorems or postulates that are most likely on your list, it is a common type of geometrical reasoning. Your class can decide what kind of language it wants to use for these types of arguments.
After all that, we have used congruent triangles to figure out why $\angle UZY \cong \angle QYZ$. However, much of the argument was probably done orally, in combination with a marked-up diagram. It is now time to
Write a formal proof of the fact that $\angle UZY \cong \angle QYZ$.
In the proof you just wrote, you took pains to make sure that each statement was correctly justified. However, it is easy to be sloppy when writing proofs. Two examples of proofs follow that illustrate some mistakes that are easy to make.
Consider the proof below showing that, if a quadrilateral has two pairs of congruent, opposite angles, then the quadrilateral is a parallelogram.
- First, draw a quadrilateral that can stand for any
quadrilateral with
congruent, opposite angles. Label the vertices $ABCD$, where
$\angle A \cong \angle C$ and $\angle B \cong \angle D$.
- Given: Quadrilateral ABCD, $\angle A \cong \angle C$,
$\angle B \cong \angle D$.
- Prove: $\overline {AB} \parallel \overline {CD} $, $\overline {BC} \parallel \overline {AD} $.
- Draw the diagonal $\overline {AC} $.
- $\angle B \cong \angle D$, as given.
- $\overline {AB} \cong \overline {CD} $ and $\overline
{BC} \cong \overline {AD} $, because opposite sides of a
parallelogram are congruent.
- Therefore, $\triangle ABC \cong \triangle CDA$ by the SAS congruence theorem.
- Then $\angle DAC \cong \angle BCA$ since they are
corresponding parts of congruent triangles.
- That makes $\overline {BC} \parallel \overline {AD} $ since alternate interior angles are
congruent.
- Similarly, $\angle BAC \cong \angle DCA$, again since
they are corresponding parts of congruent triangles.
- So $\overline {AB} \parallel \overline {CD} $.
- Therefore, $ABCD$ is a parallelogram.
This proof may seem to work quite well. However, it contains a major error that invalidates the proof entirely. What is this error?
This type of error is sometimes called circular reasoning. Why do you suppose this phrase is used?
Do you still think it’s true that, if a quadrilateral has two pairs of congruent, opposite angles, it must be a parallelogram?
Finally, here is an example of a proof that just can’t be right: if a triangle is isosceles, then it must be equilateral. You have seen lots of isosceles triangles that are not equilateral, so you know that this proof must contain a mistake! The challenge is to find out what that mistake is. Remember that, if you agree with every step of a proof, you have no choice but to accept its conclusion.
- Given: $\triangle ABC$ with $\overline {AB} \cong \overline {AC} $.
- Prove: $\overline {AC} \cong \overline {BC} $ (which would
also make $\overline {AC}$ congruent to $\overline {AB} $).
- Draw the median from $C$ and label the point where it hits
$\overline {AB} $ as $D$.
- $\overline {AD} \cong \overline {DB} $ because $\overline
{CD} $ is a median.
- Also, $\angle CDA \cong \angle CDB$ because, as a median,
$\overline {CD} $ splits $\overline {AB} $ into two right
angles.
- $\overline {CD} \cong \overline {CD} $ because any line
segment is congruent to itself.
- Therefore, by SAS congruence, $\triangle CAD \cong \triangle CBD$.
- Since they are corresponding parts of congruent triangles,
$\overline {AC} \cong \overline {BC} $.
- Therefore, all three sides of $\triangle ABC$ are congruent, making it equilateral.
Find the flaw in the proof above.
Practice
Which of the following proofs are “airtight”?
Prove that, in a quadrilateral, if
a pair of opposite sides
is both congruent and parallel, then the quadrilateral is a
parallelogram.
Proof: Draw segments $\overline {AB} $ and $\overline {CD}
$ so as to be congruent and parallel. Connect points A and
C. Then connect points B and D. Because $\overline {AB} $ and $\overline {CD} $ are congruent and parallel,
the line segments $\overline {AC} $ and $\overline {BD} $ have to slope in the
same direction. Therefore, $\overline{AC} \parallel \overline{BD}$, and so ABCD is a
parallelogram.
Prove that the diagonals of a
rhombus bisect each other.
Proof: We’ve already proven, and put on our theorem list,
that the diagonals of a parallelogram bisect each other. A
rhombus is a type of parallelogram. Therefore, any
statement
that applies to a parallelogram also applies to a rhombus,
and so the diagonals of a rhombus bisect each other.
Prove that the diagonals of a
parallelogram bisect each other. (We’ve already proved this,
but here is an alternate version of a proof.)
Proof: Draw parallelogram $ABCD$, and add diagonals that
cross at E. We’re going to show that triangles $AED$ and
$CEB$ are congruent. The two pairs of angles needed for
congruence are $\angle DAE \cong \angle ACB$ and $\angle
ADB \cong \angle DBC$.
Those pairs really are congruent because they are both pairs
of alternate interior angles created by parallel lines and a
transversal. Also, sides $\overline {AD} $ and $\overline
{BC} $ are congruent because they are opposite sides of a
parallelogram. So now we have enough to show triangles $AED$ and $CEB$ are congruent, by ASA. Therefore, the diagonals do
bisect each other: $\overline {DE} \cong \overline {EB} $ and $\overline {AE} \cong \overline {EC} $ as they are
corresponding parts of congruent triangles.
The following are situations in which you might want to add an extra line to a diagram to help you with a proof. For each situation, say whether there could be multiple lines that fit the description, exactly one line that would fit the description, or whether a line that fits the description might not exist at all.
Given line line $AB$ and point $C$ not on it, draw a line segment from $C$ to $AB$.
Given line $AB$ and point $C$ not on it, draw a perpendicular line segment from $C$ to line $AB$.
Given line $AB$ and point $C$ not on it, draw a line through $C$ parallel to line $AB$.
Given parallelogram $ABCD$, draw diagonal $AC$ so that it bisects angles $A$ and $C$.
Given triangle $ABC$, draw a line segment from points $D$ and $E$, the midpoints of $\overline {AB} $ and $\overline {BC} $, respectively, so that $\overline {DE} $ is parallel to and half the length of $\overline {AC} $.
Given triangle $ABC$, draw the perpendicular bisector of side $\overline {AB} $ from $C$.
Problems
At the beginning of a lesson, you found that the diagonals of a parallelogram do not always bisect the angles from which they are drawn. How about for a rhombus? Prove it or find a counterexample.
For which of the following shapes — square, rectangle, parallelogram, trapezoid, kite, rhombus — are the diagonals always perpendicular to each other? Investigate with sketches.
For the shapes in the previous problem where the answer is “yes,” prove your response. Before beginning each proof, carefully state the given and what is to be proved. Hint: how can you possibly show that an angle is 90 degrees if you don’t know the measures of any other angles in the figure?
The angles below are called central angles of each circle. (The vertex of each angle is on the center of the circle.)
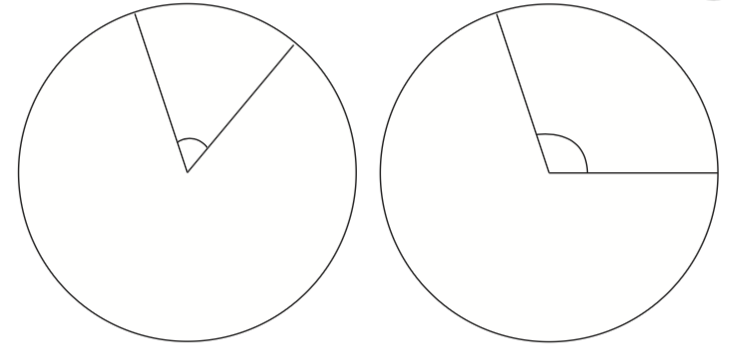
If you use a straight line segment to connect the points where the angle meets the circle, you get a chord of the circle.
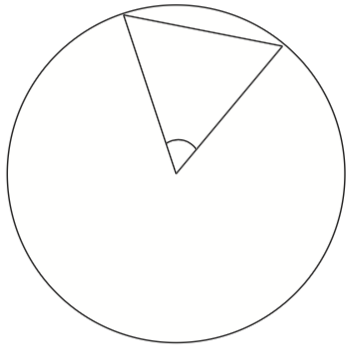
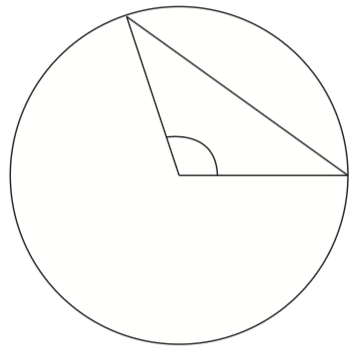
Prove that if a circle contains two central angles of the same size, then their corresponding chords are congruent.
Determine as many missing lengths and angles as you can. For each angle or length you find, give the reason you used to figure it out.

Find $x$. Write out the reasoning you used.

If you make an “X” shape in between two parallel lines, as in the figure for the previous problem, will the resulting triangles always be similar? Either prove it, or draw an “X” shape that creates non-similar triangles.
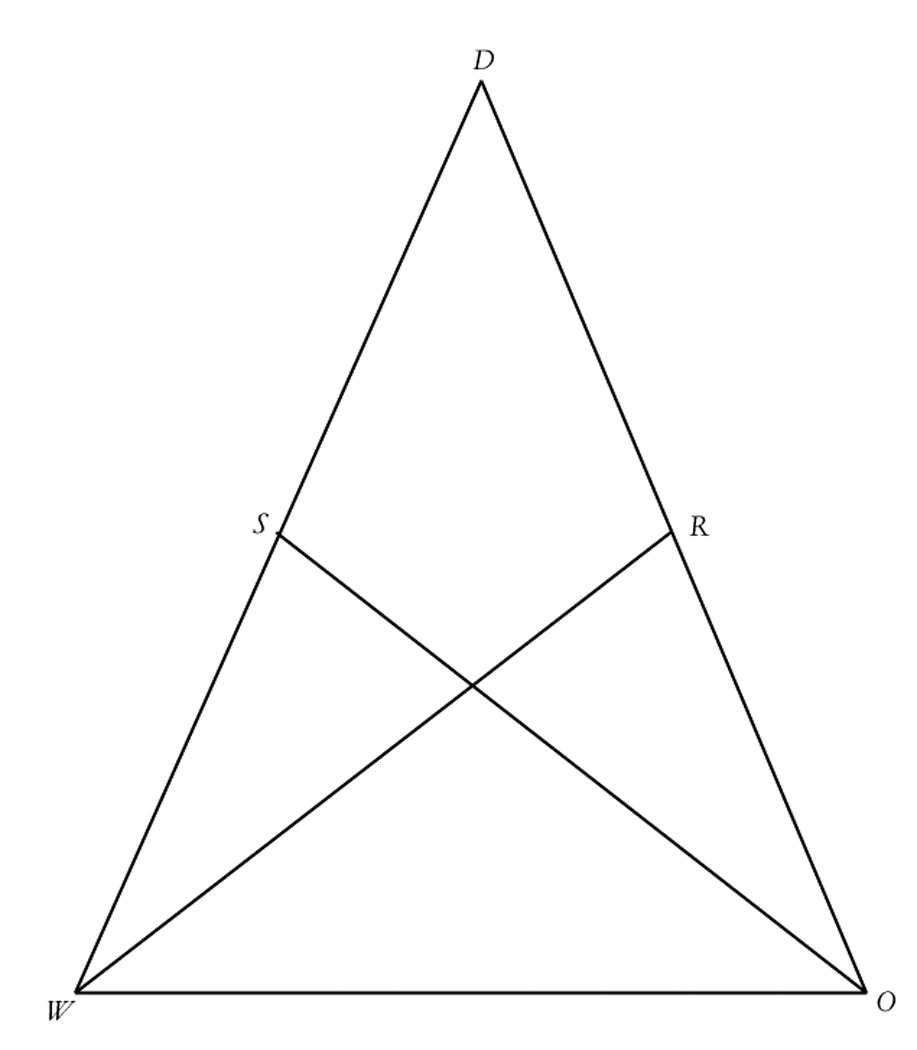
Given: S is the midpoint of $\overline {WD} $, R is
the midpoint of $\overline {DO} $. Also, $\overline {WD}
\cong \overline {DO} $.
Prove: $\overline {WR} \cong \overline {SO} $
Emmy and Sophie are standing in the center of the free throw circle on a basketball court. They want to measure their distance to the special free-throw line they put in for Emmy’s little brother — it’s a chord of the circle positioned close to the hoop.
Emmy says, “It’s easy — we just measure along a perpendicular path from where we are standing to the special free-throw line. After all, that’s how you find the distance from a point to a line.
Sophie says, “You’re right. And I think the line we measure along will not only be perpendicular to the special free-throw line, but it will bisect the line as well.”

Is Sophie right? Prove it or find a counterexample.
Suppose that Emmy and Sophie realize that they don’t have a ruler, but they remember that the radius of the circle they’re standing in is 10 feet, and the length of the special free-throw line is 14 feet. Help them calculate their distance from the line.
What’s the distance from the center of a 41-foot radius circle to an 80-foot chord?
Someone saw this circle with chord of length $2\sqrt 3 $ drawn in. They connected the endpoints of the chord to the center of the circle. Find as many lengths and angles in this picture as you can. Also find the measure and lengths of each of the 2 arcs that the chord separates the circle into.

Given: $\overline{CB} \cong \overline{CD}$ and $\overline{BA} \cong \overline{DE}$
Prove: $\angle BCF \cong \angle DCF$

Don’t use a calculator for this problem.
Simplify $\frac{{{x^{ - 3}}{y^{ - 4}}}}{{{x^2}{y^{ - 6}}}}$
Simplify $x^2 + \left( \frac34 x \right)^2$
Reduce $\frac{{3{x^2}}}{{6xy - 9{x^3}}}$
Reduce $\frac{{{x^2} - 1}}{{{x^2} - 2x + 1}}$
Solve for $x$ if ${x^2} + 1728x = 1729$
Given: $\overline{PT} \cong \overline{WT}$ and $\angle 1 \cong \angle 2$
Prove that $\triangle ZYT$ is
isosceles

Given: $ADCB$ and $EFCB$ are parallelograms.
Prove: $\triangle AEB \cong \triangle DFC$

Given: $\overline {AB} \cong \overline {CB} $, $\overline {AD} \cong \overline {DC} $
Prove that the two triangles are congruent.
Can you then show that $\overline {AD} \cong \overline {BC} $?

Let ABC be any triangle. Choose point P somewhere on side AB of the triangle, and draw a line through P parallel to $\overline {CB} $. Where this line intersects $\overline {AC} $, label the point Q.
Prove that $\frac{{AP}}{{AB}} = \frac{{AQ}}{{AC}}$.
Prove that $\frac{{AP}}{{PB}} = \frac{{AQ}}{{QC}}$.
Gina did the previous problem and wonders if it’s possible that $AP = x - 2$, $AB = x - 1$, $AQ = x - 3$, and $AC = x$. What should you tell her? Provide two explanations:
The first explanation should involve solving an algebraic equation.
The second explanation should involve considering a proportion.
The diagram below was formed by starting with any old quadrilateral, then connecting the midpoints of each side.

Try this several times on your own, with many different quadrilaterals. Form a conjecture about what always happens.
Prove your conjecture. (Hint: this is a problem where adding extra lines is helpful.)
Exploring in Depth
Given: $\overline{RS}$ is the
perpendicular
bisector of $\overline{PQ}$, and $\angle PST \cong \angle QSV$
Prove: $\overline{ST} \cong \overline{SV}$

Draw triangle ABC, and choose X to be a point on $\overline {AB} $. Draw $\overline {CX} $. Now add two lines to the picture that are parallel to $\overline {CX} $: one through A and the other through B. Y is the point where the first added line intersects line CB. (You may need to extend $\overline {CB} $ to find this point.) Z is the point where the second added line intersects line AC.
Now you have the line segments $\overline {AY} $, $\overline {CX} $, and $\overline{BZ}$ . This problem will lead you towards proving a relationship between the lengths of those three segments.
Find two pairs of similar triangles in this figure, each pair involving the segment $\overline {CX} $.
Your two pairs of similar triangles allow you to write two proportions. Using these proportions, and facts such as $AB = AX + XB$, find an equation that relates $\overline {AY} $, $\overline {CX} $, and $\overline {BZ} $.
Prove that your answer is equivalent to $\frac{1}{{AY}} + \frac{1}{{BZ}} = \frac{1}{{CX}}$.

