Introduction
Lewis Carroll, of Alice in Wonderland fame, made the following set of statements in his less famous book, Symbolic Logic.”
No potatoes of mine, that are new, have been boiled. All my potatoes in this dish are fit to eat. No unboiled potatoes of mine are fit to eat.
What, if anything, can you conclude from these three statements?
Development
It’s a well-known fact that all squares are rectangles, but not all rectangles are squares. We can express these statements in the form below.
If a figure is a square, then it is a rectangle. (true)
If a figure is a rectangle, then it is a square. (false)
You may recall that these statements are called converses of each other, as is true of any pair of statements of the form
If $A$ then $B$.
If $B$ then $A$.
You may have seen Venn diagrams at some point in your life. They are handy when thinking about logic. For instance, the statement “All business people are savvy” (or “If a person is a businessman, then he is savvy”) can be represented by the following diagram:
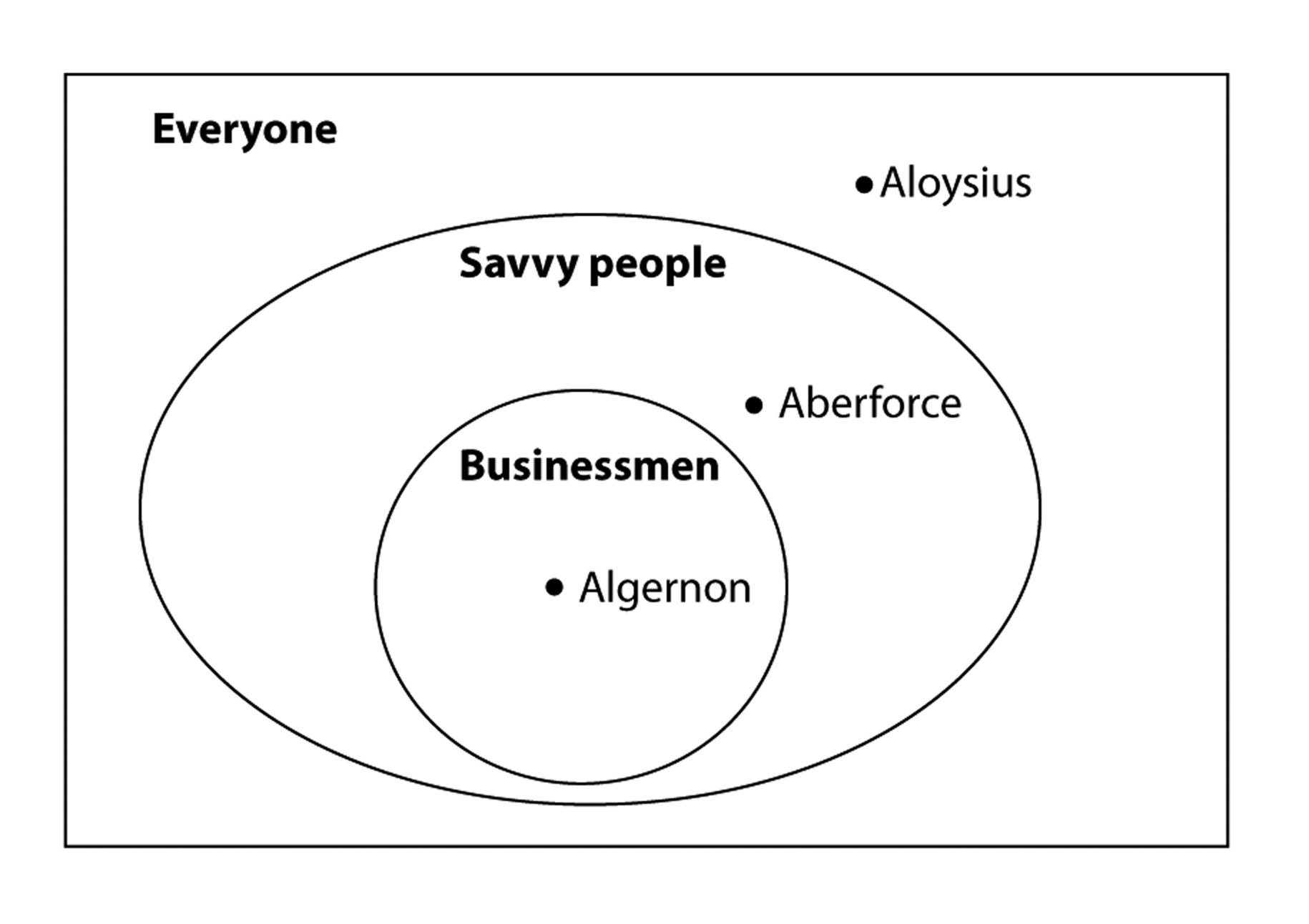
In this example, Algernon is a savvy businessman, Aberforce is savvy but not a businessman, and Aloysius is neither savvy nor a businessman.
Draw a similar diagram illustrating the statement “All savvy people are businessmen.”
How would you write the statement in “if/then” form?
Do the diagrams make it clear that the statements “All businessmen are savvy” and “All savvy people are businessmen” mean different things?
You’ve seen that if/then statements have converses, and that just because the if/then statement is true doesn’t necessarily mean the converse is. Here are two other types of statements you can get from an if/then statement.
Take the statement “if $A$ then $B$”.
“If not-$A$ then not-$B$” is called the inverse.
“If not-$B$ then not-$A$” is called the contrapositive.
Pick three “test” statements of the form “if $A$ then $B$.” Then use them to decide if the inverse and/or the contrapositive must be true when the original statement is. If you’re not sure, try drawing Venn diagrams.
Some statements on your list of theorems and postulates can be written in if/then form as well, and it is worth investigating if their converses are true. For example, you probably have the following statement:
Opposite sides of a parallelogram are congruent.
Write a pair of if/then statements expressing this statement and its converse.
If you were going to prove the converse, what would be the given? What would be the result that you are trying to prove?
Go ahead and prove the statement “if a quadrilateral has both pairs of opposite sides congruent, then it is a parallelogram.” (Hint: this is a problem where adding something extra to the diagram is useful.)
Another way of saying what you just proved is that having both pairs of opposite sides congruent is sufficient for a quadrilateral to be a parallelogram. In other words, if you have a quadrilateral and you know its opposite sides are congruent, that’s enough — you don’t need to know anything else about it to know that it’s a parallelogram.
On the other hand, the original statement on your list, “Opposite sides of a parallelogram are congruent,” provides a statement that is true about all parallelograms. This kind of statement is called a necessary condition. For if you’ve got a quadrilateral without congruent opposite sides, you know you definitely don’t have a parallelogram. You’re lacking one of the necessary criteria.
Conditions aren’t always both necessary and sufficient. For example, having four right angles is necessary for a quadrilateral to be a square, but having four right angles is not sufficient for a quadrilateral to be a square. The quadrilateral might be only a rectangle and still have four right angles.
Also, conditions can be sufficient without being necessary. For example, a closed shape’s having three 60-degree angles is sufficient for the shape to be a triangle, but it is certainly not necessary that a triangle have three 60-degree angles.
What’s more, necessary and sufficient conditions don’t have to be about shapes. For example, at Park, playing soccer for all four years is sufficient to fill your athletic requirement. Also, being a senior is necessary for taking Senior Studio — you can’t take Senior Studio without being a senior.
Is having four congruent sides necessary, sufficient, or both for being a square?
Is having four congruent sides necessary, sufficient, or both for being a rhombus?
Is playing soccer all four years a necessary condition for Park students to satisfy their athletic requirement? Is being a senior at Park sufficient for taking Senior Studio?
Practice
Poet Li-Young Lee says “every wise child is a sad child.” According to him, is being a wise child sufficient for being a sad child?
Is being seventeen sufficient for having a provisional driver’s license in Maryland?
Is being an even number necessary for being divisible by eight?
Is being a pair of numbers’ LCM…
…sufficient for being divisible by each of those numbers?
…necessary for being divisible by each of those numbers?
Is being divisible by 108 a sufficient condition for a number to be divisible by 8? By 6? by 54?
You’re organizing your little sister’s blocks. While doing so, you make the following Venn diagram to classify them. Say whether each statement is true.
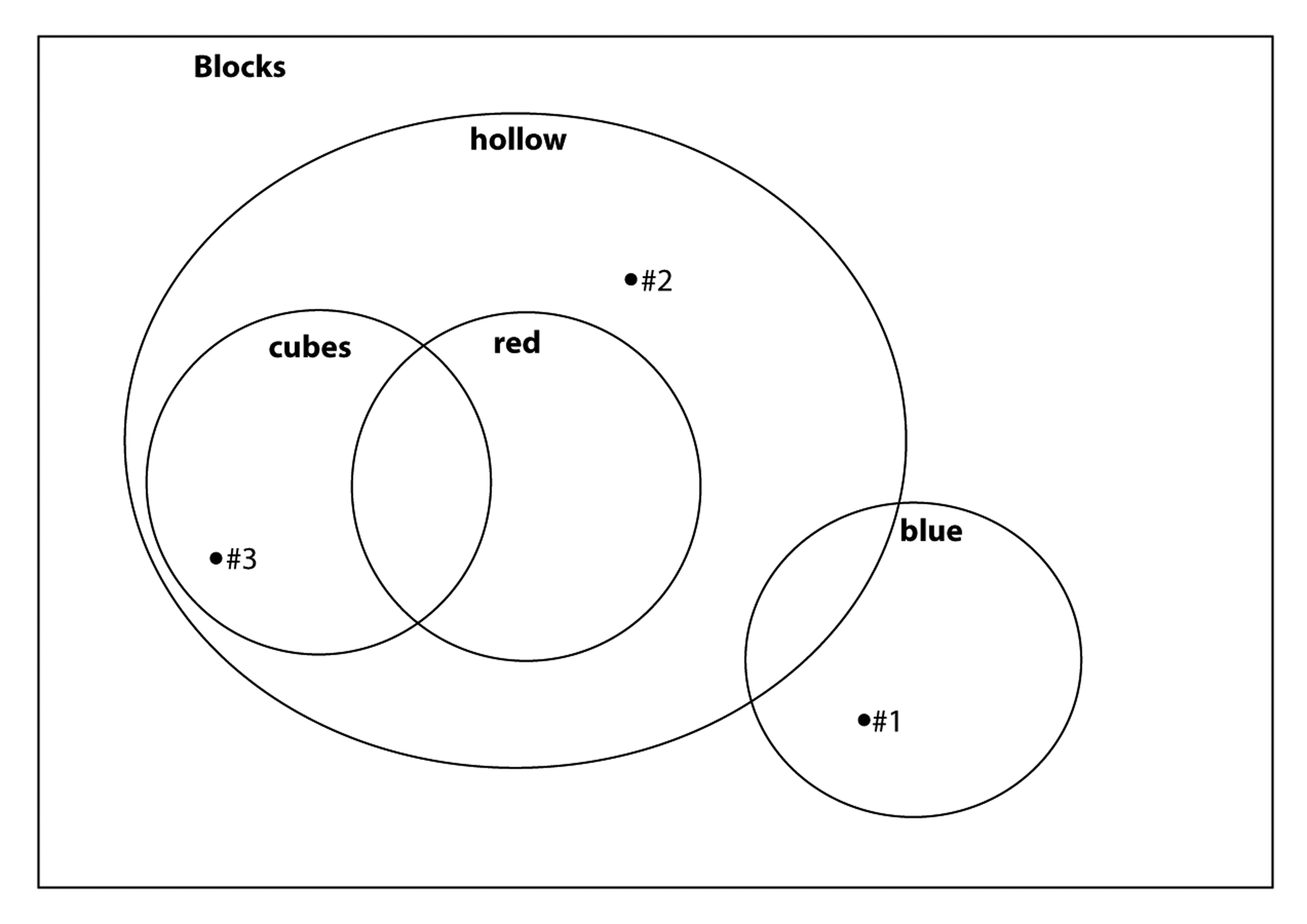
If a block is blue, then it is hollow.
If a block is red, then it is hollow.
If a block is hollow, then it is red.
Three of your sister’s blocks are shown in the Venn diagram. Describe each block according to the characteristics described in the picture.
Bill and Ted come up with the following classification system of the students attending their high school.

According to their scheme,
Is being hip necessary for being far-out?
Is being groovy sufficient for being far-out?
Is being a space-cadet necessary for being far-out?
Is being far-out necessary for being hip?
Draw a diagram (perhaps a Venn diagram or a “tree” diagram) that clearly indicates which quadrilaterals are types of other quadrilaterals (for instance, a square is a type of rectangle).
Problems
Draw a Venn Diagram and use it to see what you can conclude from the following Lewis Carroll puzzle.
- All babies are illogical.
- Nobody is despised who can manage a crocodile
- Illogical persons are despised.
The statement “no circle is a parallelogram” can’t be represented in a Venn diagram as a circle within a circle.
Write “no circle is a parallelogram” as an if/then statement.
Draw a Venn diagram that you think captures the meaning of the statement.
Write the converse, inverse, and contrapositive of that statement. Does the same diagram work for the contrapositive?
In the last lesson you proved that if you have two central angles of the same size in a circle, then their corresponding chords are congruent.
Is the converse of this statement true?
Either prove the converse or provide a counterexample.
In the last lesson you proved that if you draw a line from the center of a circle perpendicular to a chord, the line would bisect the chord.
Write the converse of this statement in a form that you might be able to prove.
Is the converse true?
Either prove it or provide a counterexample.
Euclid’s fifth postulate is famous for being more complicated than his others. The postulate is similar to the statement
If, when two lines are cut by a transversal, the alternate interior angles are not equal, then the lines will meet.
Euclid also proved a theorem which states
If, when two lines are cut by$ a $transversal, the alternate interior angles are equal, then the two lines are parallel.$
How are these two statements related to one another? (Converse? Inverse? Contrapositive?)
Did Euclid need to prove the second statement separately, or would it have been enough to appeal to the first statement?
Dr. Gordon says, “Say you have a statement like ‘if $p$ then $q$’. If this statement is true, then $p$ is sufficient for $q$ and $q$ is necessary for $p$.”
Test this condition out by trying some examples of statements (like, “If you live in Baltimore, then you live in Maryland.”)
Explain, in language that an eighth-grader could understand, why Dr. Gordon’s claim is true.
In the 2008 presidential campaign, some people were worried about whether Obama could still be a good president even though he lacked military experience. At the same time, General Wesley Clark pointed out that, though McCain had impressive military experience, that experience didn’t necessarily prepare him well for the presidency.
Are Obama’s critics arguing that military service is necessary to become a good president, or sufficient for being a good president?
Is Wesley Clark arguing that military service is not necessary to become a good president, or that it is not sufficient?
Decide if each of the following is a sufficient condition for a quadrilateral to be a parallelogram. You can think of these as “tests” to decide if the shape is really a parallelogram.
Both pairs of opposite angles are congruent.
When you draw a diagonal, a pair of alternate interior angles is congruent.
One pair of opposite sides and one pair of opposite angles are congruent.
Two pairs of adjacent (next to each other) angles are supplementary.
One pair of opposite sides is both parallel and congruent.
Two of the statements in the previous problem are true. Write a proof of each of them. (If you’re stuck on a proof, work backwards; what do you need to show in order to show that something is a parallelogram? What tools do you have to show those things?)
Draw a Venn diagram to illustrate the following statements:
If you can make it through War and Peace, you’re a superstar.
If you’re not a superstar, you can’t make it through War and Peace.
In either diagram, can you have not read War and Peace and yet still be a superstar?
Being an ack is a necessary condition for being a kook. Being an ook is a sufficient condition for being an ack. There are 22 acks, 7 ooks, and 10 kooks. Of the acks, 8 are neither ooks nor kooks. Now, supposing you pick a random ack, what is the probability that it will be an ook, but not a kook?
Investigate the following:
Draw a bunch of quadrilaterals where the diagonals are perpendicular and where one diagonal bisects the other (but not necessarily the other way around). It may help to start with the diagonals, then draw in the rest of the shape around them. What shape do these always turn out to be?
Prove that all quadrilaterals with perpendicular diagonals, one bisecting the other, are this shape.
Did you just find a necessary condition for a quadrilateral to be this shape, a sufficient condition, or both?
Name some necessary conditions for a shape to be a rhombus.
Are the conditions you named in the previous problem on your theorem list already? If the class agrees, add them to your theorem list.
Suppose that someone asked you to prove that, if a quadrilateral is not a parallelogram, at least one pair of opposite sides must not be congruent. Explain why you wouldn’t have to do a lot of work, even though this statement is not on your theorem list.
In 9th grade, you learned about a made-up rule, $a \triangle b$, which takes the first number, adds the second number to it, adds the first number to the sum, then takes that whole answer and multiplies it by the second number. For example, $7 \triangle 2$ is 32.
Also in 9th grade, a mysterious fellow named John claimed: “To get an odd number for your answer from $a \triangle b$ , you need to input odd numbers for $a$ and $b$. Did John get it right?
Did he identify a necessary or a sufficient condition for getting an odd number, or was his condition both necessary and sufficient?
The symbol "&" from the 9th grade means that you take the first number and then add the product of the numbers. About this symbol, John claimed: “To get an odd number for your answer from $a$&$b$, you need to input an odd number for $a$ and an even number for $b$.”
Did John get this one right?
Did he identify a necessary or a sufficient condition for getting an odd number, or was his condition both necessary and sufficient?
Rational numbers are those numbers that can be expressed as a fraction (where both numerator and denominator are integers and the denominator doesn’t equal 0, or a repeating decimal (like 4/3, .256256256..., and 8.000000...). Many roots (such as square roots, cube roots, and higher roots) are not rational. Some roots of integers work out to be integers themselves, like $\sqrt[4]{{16}} = 2$. However, roots of integers that don’t themselves work out to be integers are never rational; instead, they can be expressed as non-repeating decimals. Examples of these are $\sqrt 2 $ and$\sqrt[3]{7}$.
Since all numbers can be expressed as repeating or non-repeating decimals, can we conclude that all numbers are either rational or the root of an integer?
Recall from your study of quadratic equations that, so long as $a \ne 0$, the equation $a{x^2} + bx + c = 0$ has as its solutions $x = \frac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}$.
What is the converse of this statement? Is it true?
If the converse is true, then prove it. If it is not true, find a counterexample.
Update your theorem list with some of the sufficient conditions you have proven in this lesson.
Exploring in Depth
Many arguments have this type of structure:
- If a Park Student is in fall semester of 10th grade, then they are taking a “Writing about…” class.
- Gwendolyn is in fall semester of 10th grade.
- Therefore, Gwendolyn is taking a “Writing about” class.
Aristotle, a Greek philosopher who lived close to the time of Euclid, called this a syllogism. A syllogism has the form
- If $A$ then $B$
- $A$
- Therefore, $B$.
In this example, the statements “if $A$ then $B$” and “$A$” are called premises and “therefore, $B$” is called the conclusion. Note that if an argument really works, if you agree with the premises you should also agree with the conclusion. (And if you don’t, that’s a sign that something is wrong with the argument!)
Another form of argument can lead you to form an “if/then” statement as the conclusion. For example,
- If a Park Student is in fall semester of 10th grade, then they are taking a “Writing about…” class.
- If a student is taking a “Writing about” class, then they have to write a self-reflection.
- Therefore, if a Park student is in fall semester of 10th grade, then they have to write a self-reflection.
This type of argument has the form
- If $A$ then $B$
- If $B$ then $C$
- Therefore, if $A$ then $C$.
Note the important thing that allows you to conclude the final step is that “B” occurs as the “then” clause of the first statement and the “if” clause of the second statement.
Boiling arguments down to their logical structure can be handy, especially when you start using the equivalence of the contrapositive. For example, recall the Lewis Carroll puzzle of problem #18:
- a) All babies are illogical.
- b) Nobody is despised who can manage a crocodile.
- c) Illogical persons are despised.
Suppose you have managed to rewrite the puzzle this way:
(from a and c) If you are a baby, then you are despised
(from b) If you can manage a crocodile, then you are not despised.
Right now the premises are written as
If $A$ then $B$.
If $C$ then not-$B$.
It’s difficult to know what we can conclude just now, but if we replace the second premise with its contrapositive, “if $B$ then not-$C$,” we can make things match up in the right way:
- If you are a baby, then you are despised.
- If you are despised, then you cannot manage a crocodile.
This allows us to easily see that we can conclude
If you are a baby, then you cannot manage a crocodile.
…which is the solution to the puzzle.
For exercises 38-41 and 43-46, say what, if anything, you can conclude from the premises given.
If you are on Park’s basketball team, then you are over six feet tall. If you are over six feet tall, you can’t go on the Pirate ride at Six Flags.
If you live in Baltimore, you should go see an Orioles game. If you don’t like baseball, then you shouldn’t go see an Orioles game.
If it snows a lot, they’ll cancel school. If they don’t cancel school, I’ll scream.
If Tom committed the murder, he was in the library at 10 last night. If Tom wasn’t in the library at 10 last night, then he was at home.
Don’t use a calculator for this problem.
Simplify $\sqrt {4{a^2}} $
Factor ${x^2} + 3x - 28$
Find $x$ if $\frac{{17x}}{{3x + 2}} = 5$
Expand ${(x + 2)^3}$
Simplify ${(\frac{{{w^5}{x^{ - 2}}y}}{{{{(w{x^2})}^2}{y^{ - 1}}}})^2}$
If Jean committed the murder, she was in the library at 10
last night.
If Jean bought groceries on her way home, then she wasn’t in
the library at 10 last night.
All brilliant mathematicians have a heart of gold.
If you study for hours, then you don’t have a heart of
gold
If you don’t file a form, you can’t get
good service.
All people who get good service are
content.
This puzzle comes from Lewis Carroll, author of Alice in
Wonderland.
(note: “affected” means “written in a snobby, insincere
way”)
(other note: assume that all poems are either ancient or
modern)
No affected poetry is popular among people of real taste.
No modern poetry is free from affectation.
No ancient poem is on the subject of soap-bubbles.
All your poems are on the subject of
soap-bubbles.
Part c of problem #25 might have seemed true. (“One pair of opposite sides and one pair of opposite angles is sufficient for a quadrilateral to be a parallelogram.”) What goes wrong when you try to attempt a proof? Does this suggest a method for finding a counterexample?
In fact, P. Halsey published the following “proof” that one pair of opposite sides and angles in a quadrilateral was sufficient for it to be a parallelogram, challenging his readers to find the flaw. Can you?

(source: Jim Loy’s puzzle pages: http://www.jimloy.com/geometry/quad.htm)
Given: $\overline {CD} \cong \overline {AB} $, $\angle A
\cong \angle C$.
Prove: $ABCD$ is a parallelogram.
Draw perpendiculars from points B and D that intersect the opposite sides of the quadrilateral at E and F, respectively. Then $\Delta DCF \cong \Delta BAE$ by AAS. Since the triangles are congruent, $\overline {AE} \cong \overline {CF} $.
Also, from the triangle congruency we know $\overline {BE} \cong \overline {FD} $ as well. This means that we can now show $\Delta DEB \cong \Delta BFD$ by Hypotenuse-Leg. From this, we can conclude $\overline {DE} \cong \overline {FB} $.
Now, the lengths of $\overline {DE} $ and $\overline {EA} $ add up to the length of $\overline {DA} $, and likewise the lengths of $\overline {BF} $ and $\overline {FC} $ add up to the length of $\overline {BC} $. Since $\overline {DA} $ and $\overline {BC} $ are made up of the same-sized “pieces”, they must themselves be congruent. Therefore, $ABCD$ is a parallelogram.