Introduction
In this chapter, you have proven many properties of triangles and quadrilaterals. You’ve known about some of these properties for a long time; others may have been new to you. You have also set about creating a structure for the geometry you know, choosing certain facts to consider as basic and showing how other facts depend on those. At this point, you are well beyond the basics, and you have probably already begun to make conjectures about ideas you haven’t thought about before.
In your notebook, use a compass to draw a circle. Then draw two chords of two different lengths that cross somewhere inside the circle. Label the endpoints of one chord $A$ and $B$, and the endpoints of another chord $C$ and $D$. The chords cross at point $E$. Now measure $\overline {AE} $, $\overline {EB} $, $\overline {CE} $, and $\overline {ED} $. Try calculating $AE \cdot EB$ and $CE \cdot ED$. What do you find?
In this section, most ideas that come up will probably be new, and many, like the result above, will be unexpected. You will be in a good position to make some conjectures and to prove many of the conjectures you make.
After looking at parallel lines, triangles, and quadrilaterals, we’ll now turn our attention to circles. Many of the theorems you’ve already established will prove useful in investigating circles. Circles themselves often prove useful in analyzing other shapes, as you’ve probably realized when doing compass-and-straightedge constructions. In the development, most of your time will be spent learning the substantial vocabulary that has to do with circles. Then you’ll learn and prove a few basic properties of circles. In the problems section, you will have freer rein to conjecture and prove more things about circles, and about geometry in general.
Development
Your submarine has a rotating radar beam that is used to get a picture of the surrounding area. Your radar screen looks like this,

with the bold line segment showing the motion of the radar beam. As the beam rotates, the screen updates based on what the beam finds.
Why do you think the radar screen is in the shape of a circle, rather than, say, a rectangle?
Say that you know that the circle the screen makes has a circumference of 360 millimeters. What’s the length of the edge of the screen that has been updated since the beam was pointing due east? Answer this question for each picture below.
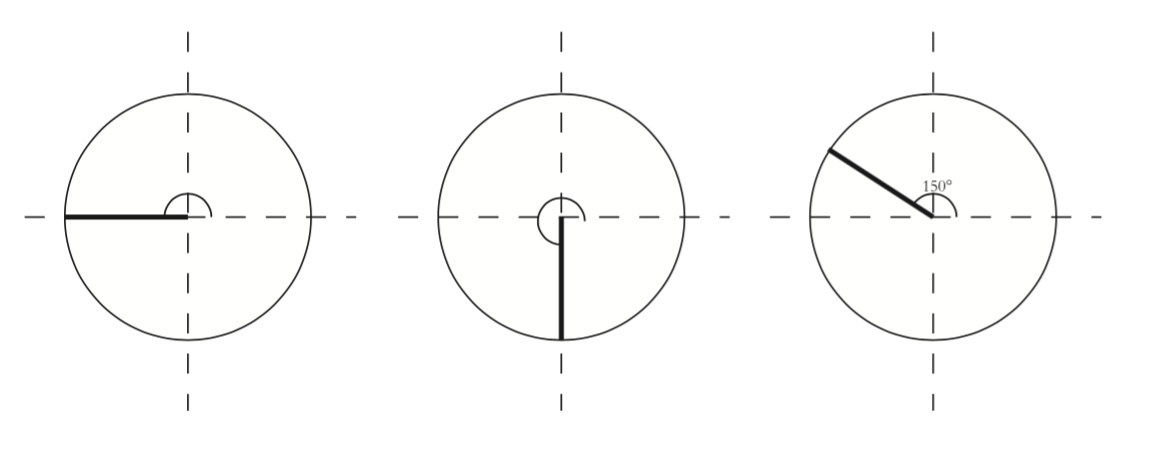
Recall that the ${150^ \circ }$ angle in the rightmost picture on the previous page is called a central angle. As you can see, there’s a direct relationship between a central angle and the arc it intercepts, even if the circumference of the circle is not 360 millimeters.
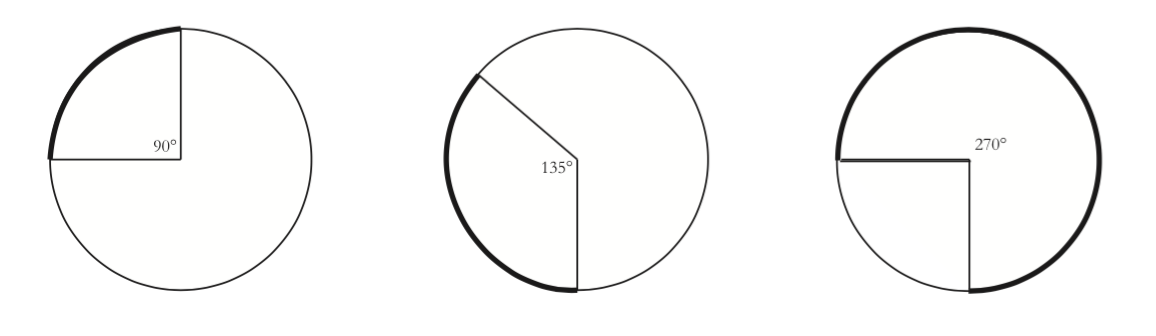
Because of this relationship, people also talk about the angular measure of an arc. The measures of the arcs above are ${90^ \circ }$, $135^\circ$, and ${270^ \circ }$ . So both of the arcs below have measure ${90^ \circ }$, even though their lengths are very different.

What’s the measure of the arc that borders the portion of the radar screen between east and northwest?
What’s the measure of the arc that borders the portion of the radar screen between north and south-southeast?
If an arc of a circle has measure ${47^ \circ }$, what’s the measure of the arc you’d need to form the rest of the circle?
To refer to an arc, you use the two points where the arc begins and ends. Here’s arc AB, or, better yet, $\newcommand{arc}[1]{\stackrel{\Large\frown}{#1}}\arc{AB}$.

Of course, when we’re talking about arcs that are parts of circles, naming arcs this way has a little problem…

…because how would we know whether we meant the arc that looks like it’s about ${90^ \circ }$, or the one that looks like it’s about ${270^ \circ }$? When you don’t specify, it’s assumed that you mean the smaller, or minor arc.
Draw a circle in your notebook. Pick points $Q$ and $Z$ anywhere on the circle. Use measuring tools (and perhaps a bit of ingenuity) to find the measure of arc $QZ$. Then describe a general strategy for finding arc measure.
Another type of angle in a circle is called an inscribed angle. An inscribed angle has its vertex on the circle, not at the center. Inscribed angles can intercept arcs, too.
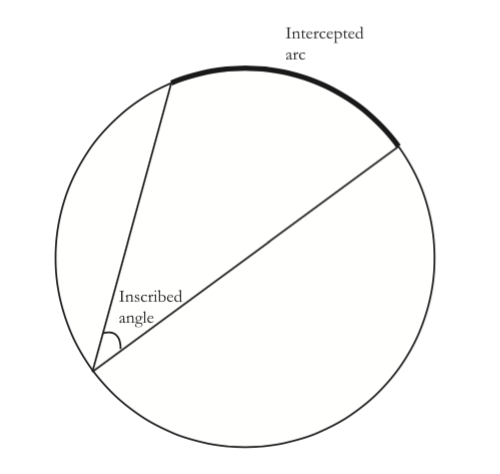
Here’s a ${45^ \circ }$ inscribed angle. Does it look like it also intercepts a ${45^ \circ }$ arc?

There is a conjecture to be found here. Draw some more circles with inscribed angles, and find it.
Now that you have a conjecture, it’s time to look for a proof. The following problems will help you.
Below is a picture of an inscribed angle $BAC$, which intercepts the same arc as central angle $BOC$.
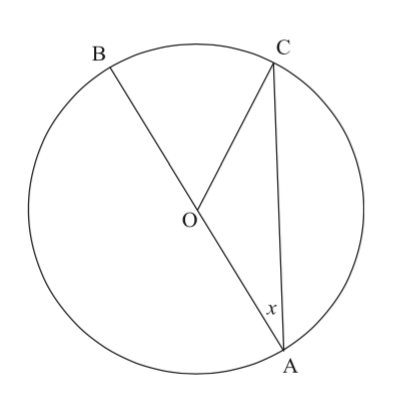
Using geometric tinkering, find the measure of $\angle BOC$ in terms of $x$.
The proof that you’ve done does not work for the diagram in problem 8. What goes wrong?
Here is another diagram, one that looks more like the situation in problem 8.
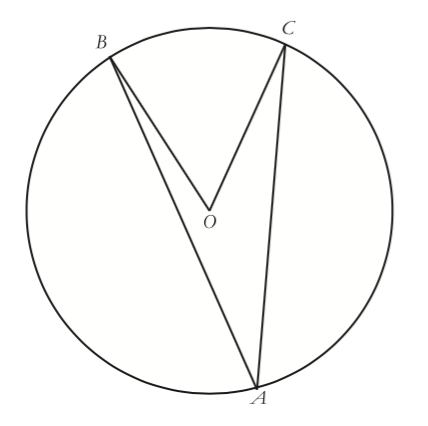
Since we already know something about when one of the sides of an angle is a diameter, let’s draw in the diameter and label the angles this way:

Using this diagram, prove that the central angle is still twice the inscribed angle.
Between problems 10 and 11, will your proofs work for all inscribed angles? If so, great. If not, draw a picture of an inscribed angle, along with its associated central angle, for which the proofs will not work.
Practice
For this problem, think of an analog clock (a clock with hands).
Find the angle determined by the hands of a clock when it is 4 o’clock. What’s the measure of the arc formed by the edge of the clock between the 12 and the 4?
Now imagine that you draw a line from the 12 to the 8 and then from the 8 to the 4. What’s the angle formed at the 8?
What’s the measure of the arc formed by the edge of a clock between the 7 and the 11?
Create an inscribed angle by starting at the 7, going to any time on the clock not between 7 and 11 o’clock, and then going to the 11. How will this compare with your angle in part c?
For each figure, find as many angles and arc measures as you can. A dot indicates the center of the circle.


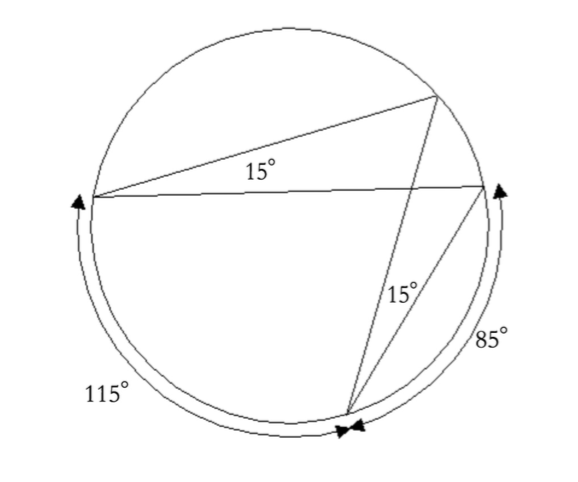
What can you say about two inscribed angles that intercept the same arc? Why?
Below is an angle formed not by two chords, but by a chord and a tangent segment. Note that this angle still can be said to intercept an arc. Make a conjecture about the measure of a chord-tangent angle and the measure of its intercepted arc.
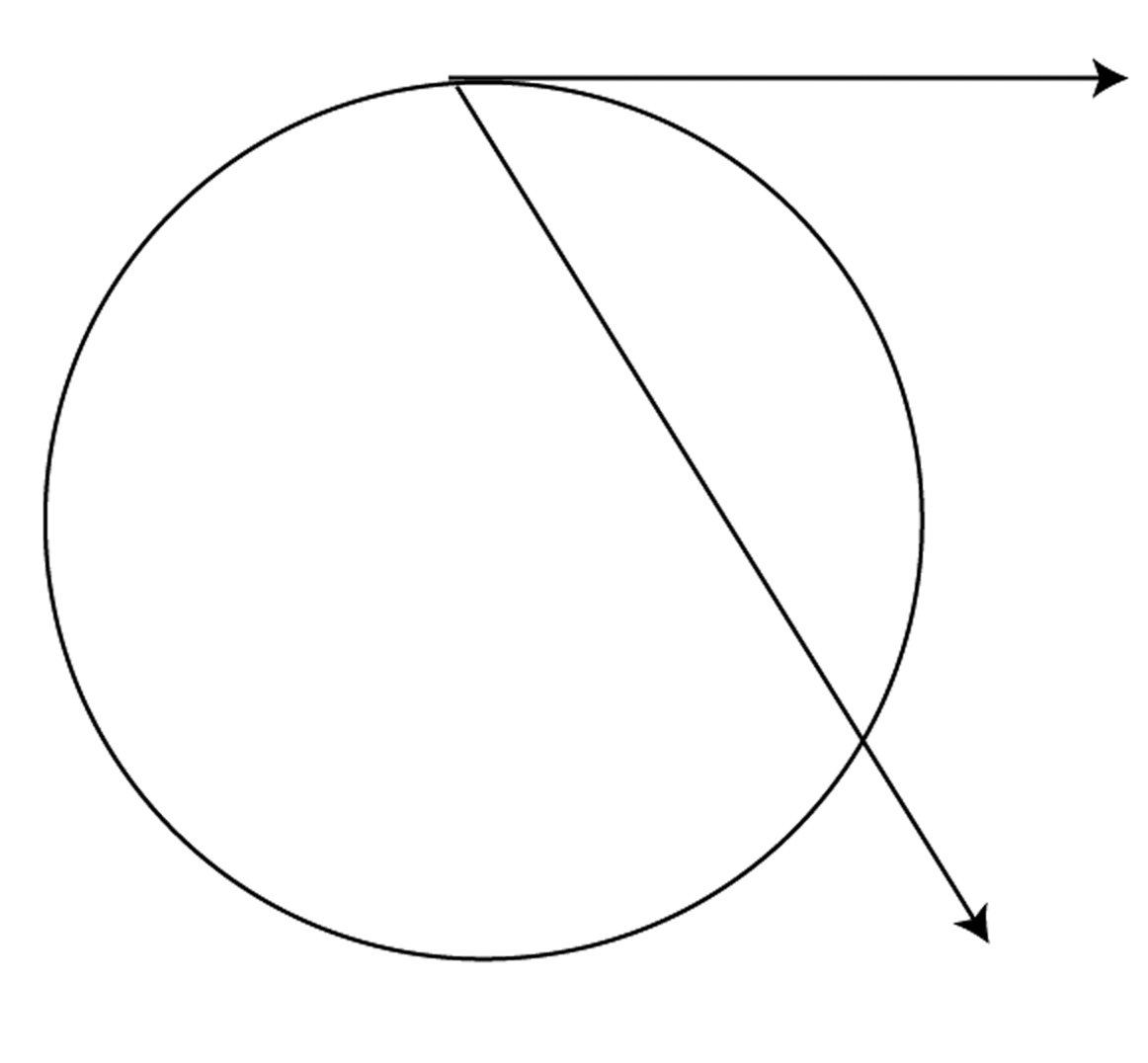
In the diagram below, $m\angle A = {\left( {{x^2}} \right)^ \circ }$ and $m\angle B = {\left( {2x + 120} \right)^ \circ }$. Find $x$.
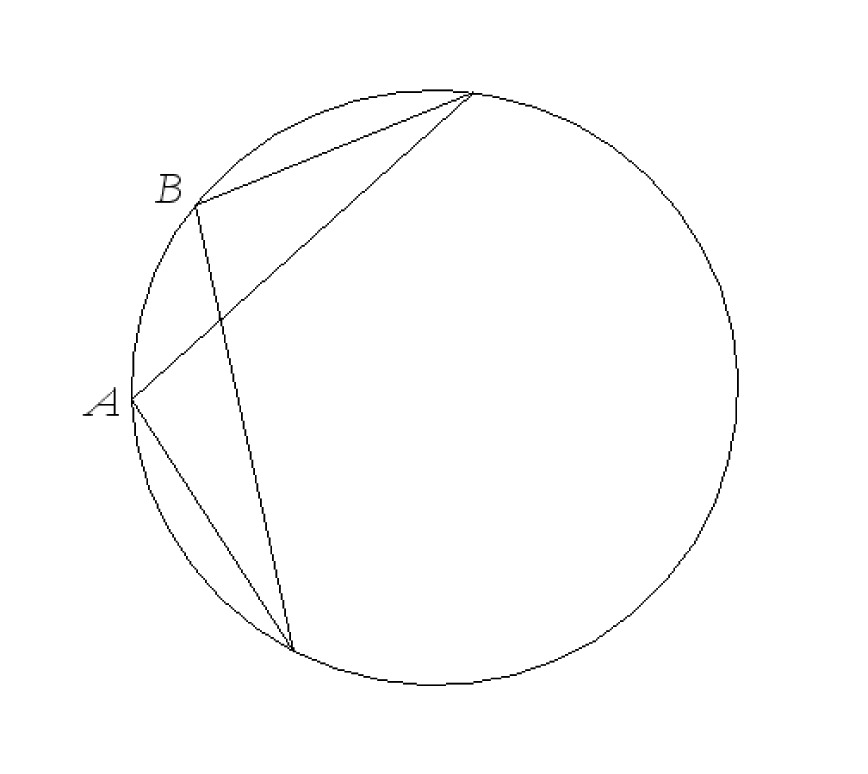
Let $m\angle A = {\left( {2x + 24} \right)^ \circ }$. Find $x$.

Q is the center of the circle, and $m\angle A = 25^\circ $. Find the measure of $\arc{AB}$.
Circle O has radius 12. Find
The measure of $\arc{AB}$.
The actual length of $\arc{AB}$.
The area of the sector of the circle COW. (What do you suppose a sector is?)

Problems
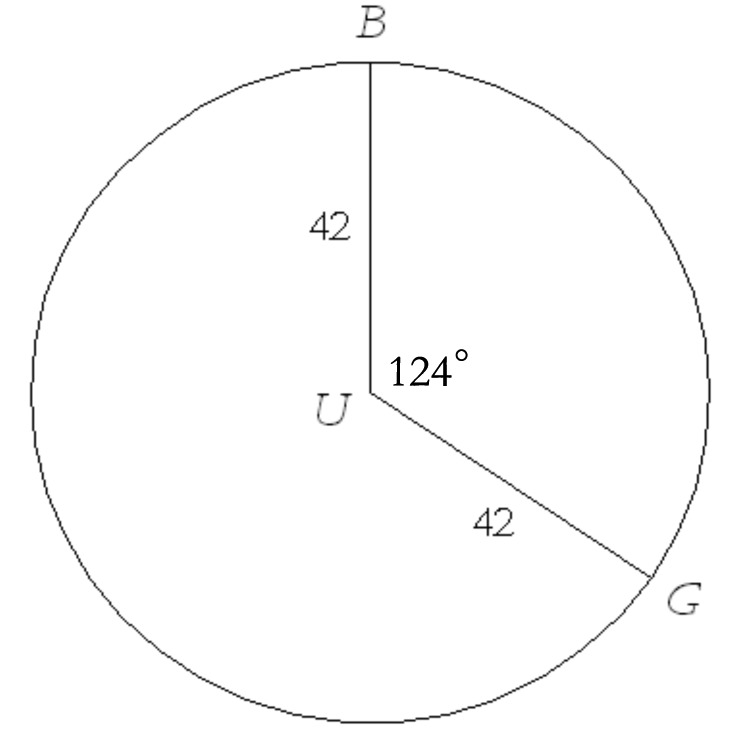
The circle below has radius 42. Find
The length of $\arc{BG}$
The area of sector $BUG$
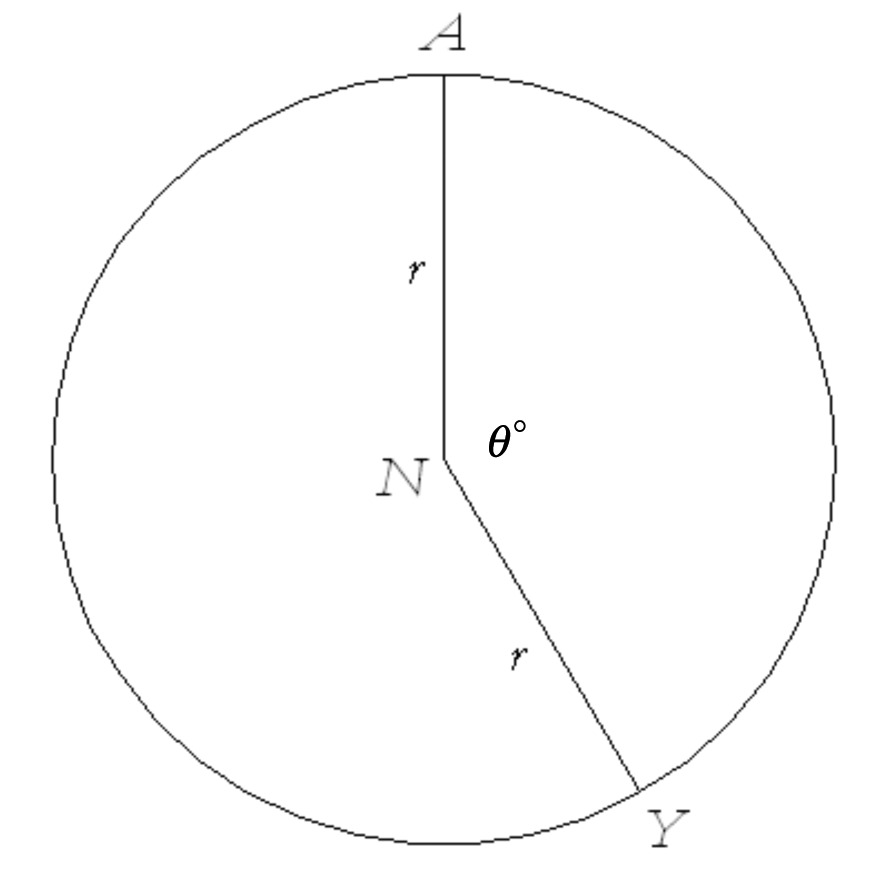
The circle below has radius $r$, and the central angle is $\theta$. Find
 .
.
The length of $\arc{AY}$.
The area of sector $ANY$.
Here’s another diagram showing a central angle and an inscribed angle that intercept the same arc.
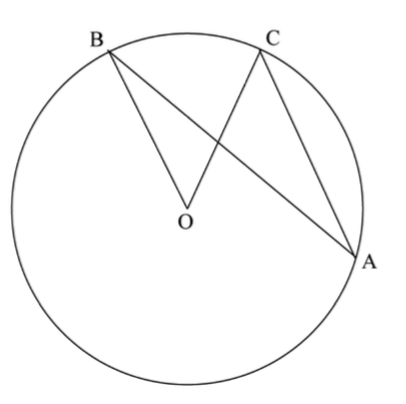
Why don’t the methods of proof you used in problems 10 and 11 work for this inscribed angle/central angle pair?
Prove that $m\angle BOC$ is twice $m\angle BAC$. As is often the case, you’ll need to act on the diagram first.
Now have you proved this result for all inscribed angles, or are there other positions for inscribed angles for which none of your proofs would work?
When you need to do separate proofs depending on the situation, that is called “proof by cases.” For example, if you wanted to prove a result in number theory, you might do different proofs depending on whether your original number was even or odd, but you would have to do both proofs in order to prove that the result always worked. Describe in words the three cases you considered when you did the inscribed angle proof.
Draw line segment AB, then accurately draw its perpendicular bisector.
Pick a few points on the perpendicular bisector and label them $C$, $D$, $E$, etc. Compare $CA$ vs. $CB$. Does this result seem to hold up consistently?
Investigate whether the converse of your conjecture in part a is true. If you are having trouble figuring out what the converse should be, try rewriting your original conjecture in “if/then” form.
The radius of a circle is 16.5 inches.
What’s the area of a 90-degree sector of the circle?
What’s the area of a 1-degree sector of the circle?
What’s the area of a 53.5-degree sector of the circle?
What’s the area of an $n$-degree sector of the circle?
In your notebook, draw$\angle XYZ$. Suppose you begin to walk a path “inside the angle,” starting at $Y$. You walk in such a way that you are always the same distance away from $\overrightarrow {YX} $ and $\overrightarrow {YZ} $. Using precise mathematical language, make a conjecture about your path.
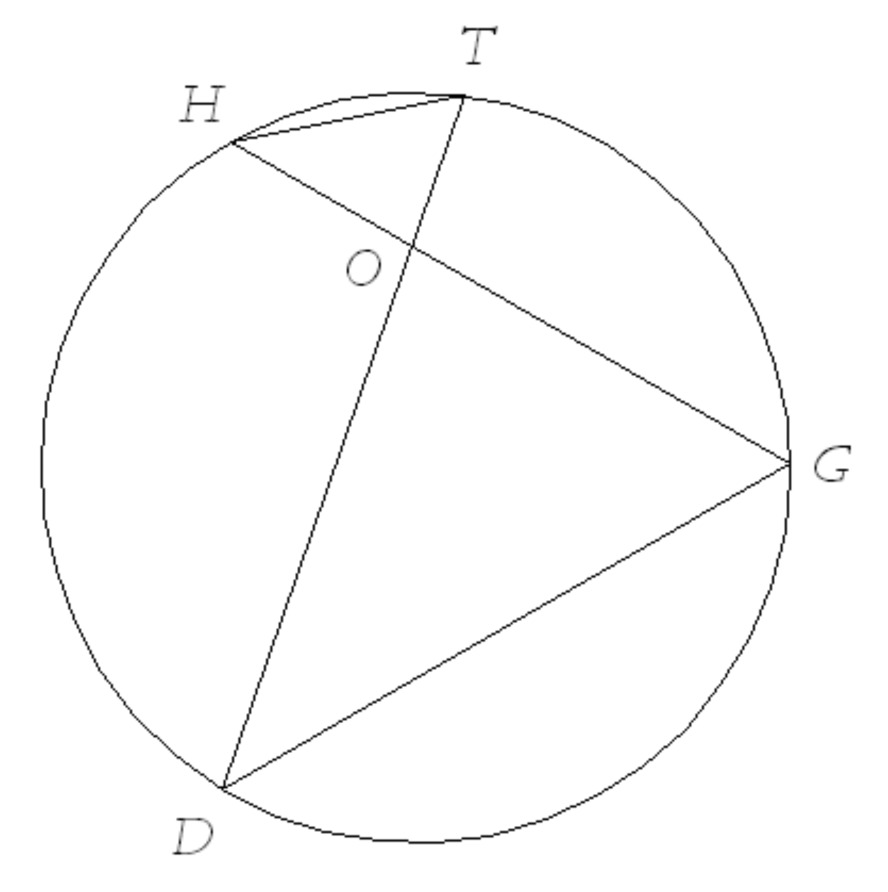
Prove that $\triangle HOT \sim \triangle DOG$.
Here is a figure designed to help you with a proof. Two proofs, actually.
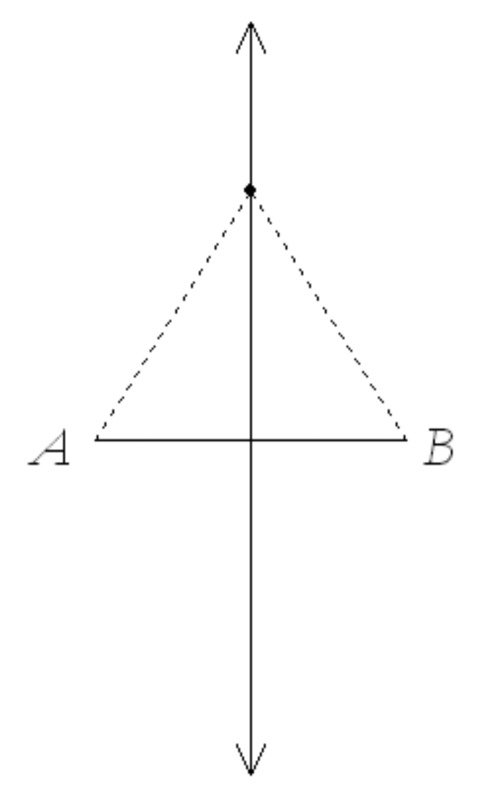
Use the figure to prove that points on the perpendicular bisector of a segment are equidistant from the endpoints of the segment. Be careful in selecting the given.
Now use the figure to prove the converse. Again, be careful in selecting the given and what is to be proved.
If you had only a compass and straightedge, but no ruler, suggest a method for drawing in the perpendicular bisector of any line segment AB. No fair folding the paper.
You cut a pizza into 10 congruent slices.
If the area of one slice is 6.5 square inches, what’s the radius of the pizza?
If instead the perimeter of one slice is 17 inches, what’s the radius of the pizza? (If you’re stuck, you could write an equation first: 17=…)
Can the area of a circle ever be an integer? Why or why not?
Here is Problem 1, reprinted:
In your notebook, use a compass to draw a circle. Then draw two chords that cross somewhere inside the circle; they needn’t cross at the center of the circle. Label the endpoints of one chord A and B, and the endpoints of another chord C and D. The chords cross at point E. Now measure segment $\overline {AE} $, $\overline {EB} $, $\overline {CE} $,and $\overline {ED} $. Try calculating $AE \cdot EB$ and $CE \cdot ED$. What do you find?
Prove the conjecture you made in Problem 1. Planning this proof is a great opportunity to work backward. What geometry tools do you have to show that two products equal one another?
Is it possible for the lengths of the four segments formed by two intersecting chords in a circle to be 4 consecutive integers?
Suppose that you have a triangle inscribed in a circle in such a way that one of the triangle’s sides is the circle’s diameter. What kind of triangle must you have, and why?
There is a theorem very similar to the one dealt with in Problem 32 about line segments drawn from a point outside a circle to a circle. (You could also think of this as a case where lines cross outside of a circle, instead of inside it.) As in the case of crossed chords, there is a product of lengths that remains constant. Which lengths are they?

State and prove a theorem based on your findings in Problem 26.
In the previous problem, did you prove a result corresponding to Problem 26, or did you prove the converse? Either way, state and prove the converse of the theorem you proved in the previous problem.
Suggest a way to construct an angle bisector using only a compass and straightedge.
Given triangle $ABC$, let $F$ be the point where segment $BC$ meets the bisector of angle $BAC$. Draw the line through $B$ that is parallel to segment $AF$, and let $E$ be the point where this parallel meets the extension of segment $CA$.
Find the four congruent angles in your diagram.
How are the lengths $EA$, $AC$, $BF$, and $FC$ related?
How are the lengths $AB$, $AC$, $BF$, and $FC$ related?
In the figure below, prove that $PB \cdot PA = PD \cdot PC$. Here are a few hints.

Show that the result you want is equivalent to $\frac{{PB}}{{PC}} = \frac{{PD}}{{PA}}$.
Part a is a sign that you should be looking for similar triangles where $\overline {PB} $ and $\overline {PD} $ are corresponding sides, and so are $\overline {PC} $ and $\overline {PA} $. Add some lines to the diagram so that triangles exist with these sides.
Now prove the result.
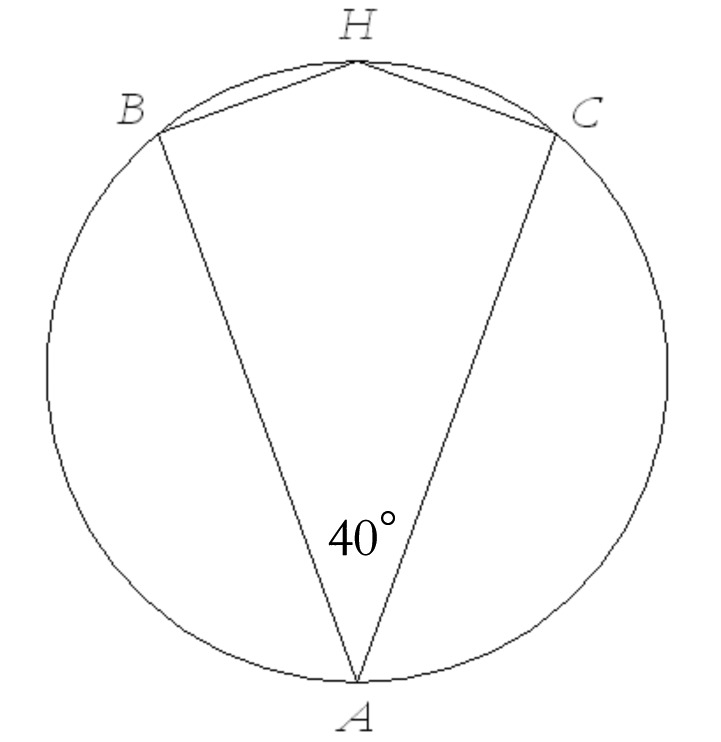
BACH is a kite inscribed in a circle. Find all the angles of the kite. (Hint: find some arc measures along the way.)
Don’t use a calculator for this problem.
Solve for $x$ if $\frac{{2x - 4}}{{{x^2} + 3x + 1}} = 0$
Simplify $\sqrt {72} $
At what point do the lines $y = 2x - 4$ and $y = -\frac{4}{7}x + 5$ cross?
Solve for $x$ if ${x^2} + 6x - 2 = 0$
If $x + y = 1729$ and $\frac{1}{x} + \frac{1}{y} = 1729$, find $xy$.
Draw several triangles of varying shapes and sizes, then construct the perpendicular bisectors of each side of each triangle. Coincidence? You be the judge.
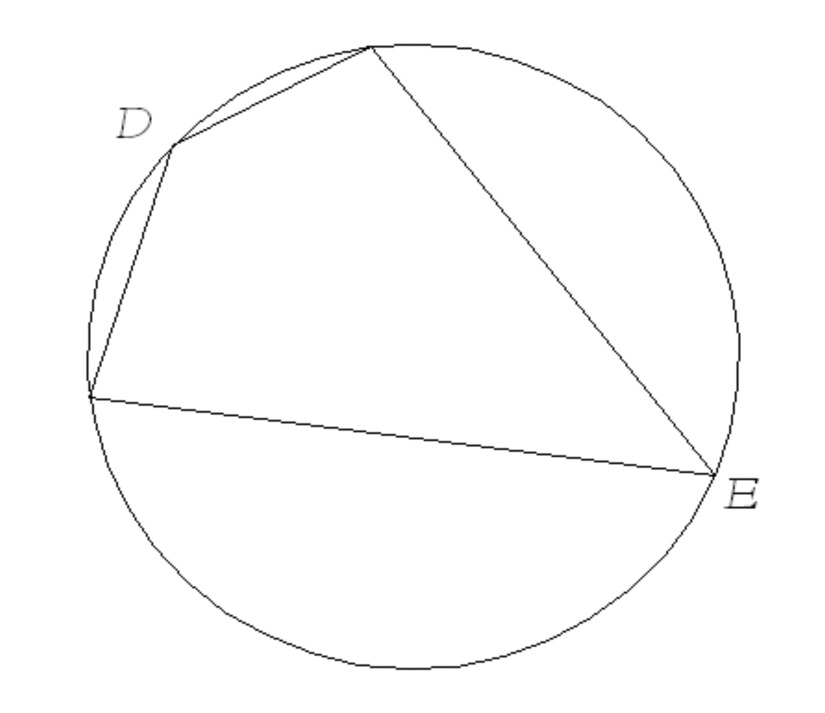
BUCK is not a kite. Find all of its angles.

Make a generalization about the opposite angles of a quadrilateral inscribed in a circle.
Let $m\angle D = {\left( {{x^2} - 10x + 60} \right)^ \circ }$ and $m\angle E = {\left( {8x + 85} \right)^ \circ }$. Find all possible values of $x$.
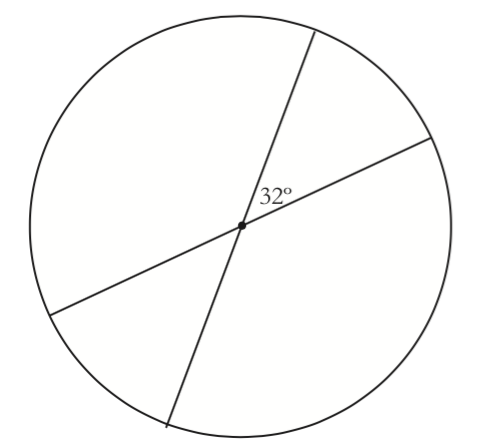
You know results about central angles and their intercepted arcs, as well as inscribed angles and their intercepted arcs. How about angles with their vertex not on the center or on the edge of a circle, but inside the circle? Make a conjecture. Hint: One way to get angles with their vertex inside a circle is to draw a pair of crossed chords.
How many lines can you draw through point P that are tangent to the circle? Try drawing lines from a point other than P. What about a point inside or on the circle?

Rotate the diagram above so that $P$ is on the bottom and the whole figure looks like an ice-cream cone. Make a conjecture about the lengths of the tangents from P.
Prove the conjecture you made in the previous problem. Do you need to have additional information? How can you create some?
The dotted line segment has a length of 13. Find the lengths and angles marked with letters. Give a reason each time you deduce something. The center is marked with a dot; lines that appear to be tangents are tangents.
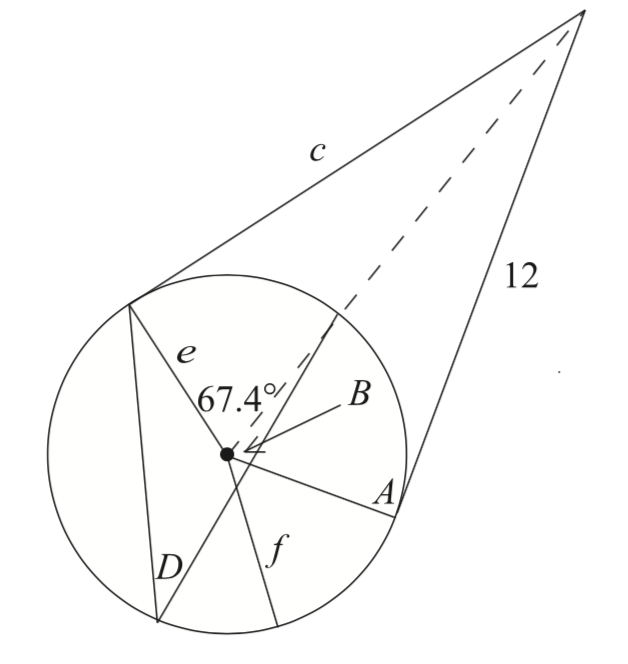
Find the lengths and angles marked with letters. (Uppercase for angles; lowercase for lengths) Give a reason each time you deduce something. The center is marked with a dot; lines that appear to be tangents are tangents.

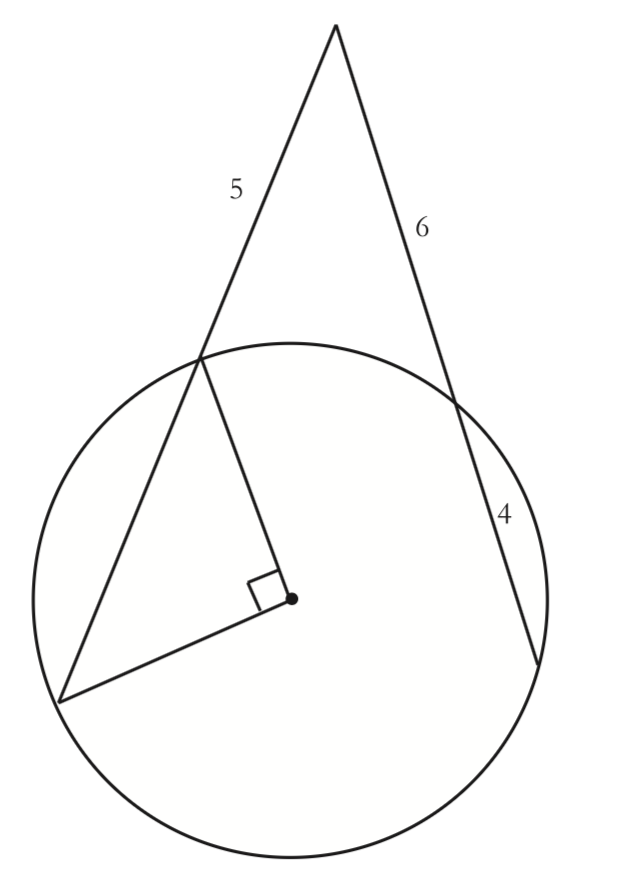
Find the exact value of the radius of the circle below.
Prove that the measure of an angle formed by crossed chords in a circle is the average of the measures of the two arcs intercepted by the two angles of that size.
Find the probability that 3 points chosen at random from $n$ points evenly spaced on a circle will form a right triangle. (Hint: simplify the problem.)
Exploring in Depth
Draw in the perpendicular bisectors for sides $AB$ and $BC$ of the triangle below. Then label the point where they cross $D$.

Is the point $D$ closer to $A$ or $B$?
Is the point $D$ closer to $B$ or $C$?
Suppose, now, that you were going to draw the perpendicular bisector of $\overline{AC}$ as well. Can you make an argument that it should pass through the point $D$, even before you draw it?
In this figure, $AB = 20,{\rm{ }}BC = 11,{\rm{ and }} DC =
14.$
Find $AD$.
(Hint: pick a side length to call $x$, then try to write the
other lengths in terms of $x$.)

Given: $\arc {NG} \cong \arc {LA}$ Prove: $\overline {AN} {\kern 1pt} {\kern 1pt} \left\| {{\kern 1pt} {\kern 1pt} \overline {GL} } \right.$

You know that every triangle has three different heights (or “altitudes”).
Use a ruler and protractor to draw in the three different altitudes for each triangle:



Come up with an argument for why, in a right triangle, the three altitudes must all meet in one point.
In each of the triangles in problem 59, the three altitudes should have met in one point. Do you think this is true for all triangles? See if you can find a counterexample.
Draw a large triangle, then draw its midpoint triangle. Draw the perpendicular bisectors of the sides of the large triangle. These lines have a significance for the midpoint triangle as well. What’s the significance, and why is this always the case?
Can you now prove that the three altitudes of any triangle meet at one point? Do so or explain why there still might be counterexamples.
Remind yourself of the result about angle bisectors you proved earlier in this lesson. Use it to prove that the three angle bisectors in a triangle meet at one point.
Prove that an angle formed by a chord and a tangent to a circle is half the measure of its intercepted arc.
Draw a point $P$ outside of a circle. Then draw two line segments from $P$: a tangent segment that hits the circle at point $A$, and a segment that intersects the circle twice, at point $B$ (farther from $P$) and $C$ (closer to $P$). Prove that $PA^2 = PB \cdot PC$.