Introduction
You’ve seen sine, cosine, and tangent before. In fact, you’ve even used them to find missing sides in triangles.
How would you define the sine of $\theta $ ? Cosine of $\theta $ ?
Use careful construction of a triangle to find $\sin {37^ \circ }$. Do not use the sine function on your calculator!
Why can’t you use a construction to find $\sin {102^ \circ }$?
Even though we can’t construct a triangle to find the sine of ${102^ \circ }$, your calculator can tell you an approximate value! In this lesson, we will discover a new way to think about sine and cosine—a way that makes calculating the values of $\sin {102^ \circ }$, $\cos 1002^\circ$, and $\tan \left( { - {{10002}^ \circ }} \right)$ possible.
Development
Most of the problems in this section require carefully drawn diagrams.
A wheel of radius one foot is placed so that its center is at the origin, and a pin on the rim is at (1, 0). The diagram below shows the wheel after it has been spun an angle ${\theta ^{}}$ in a counterclockwise direction.
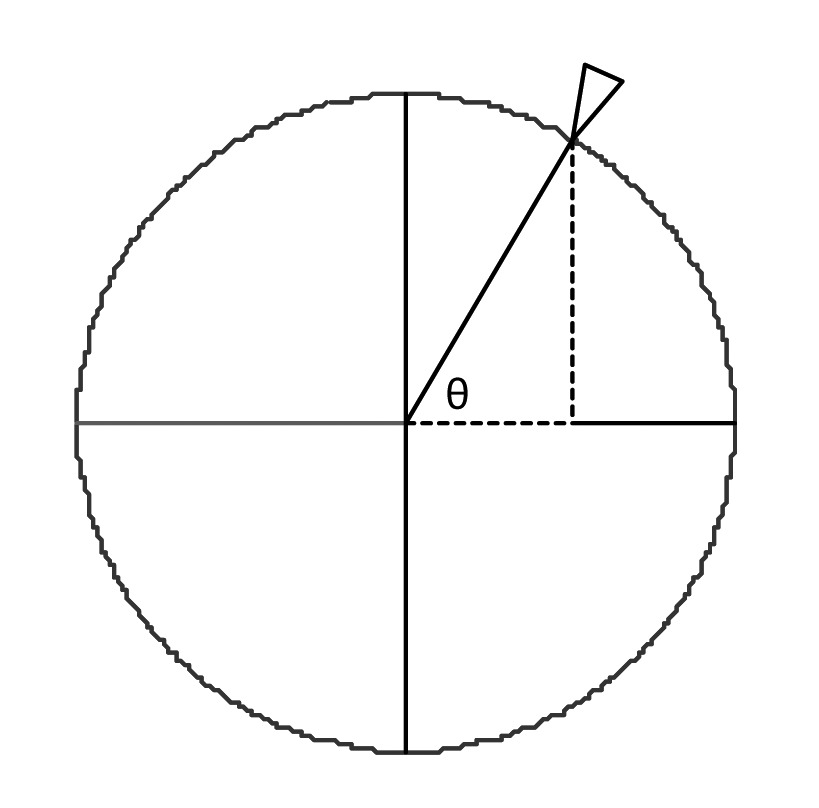
Now consider the function $P(\theta )$, which outputs the coordinates of the pin after the wheel has been spun an angle ${\theta ^{}}$ in a counterclockwise direction. So, for example, $P({0^\circ})=(1,0)$ and $P({270^\circ})=(0, - 1)$. Find $P(\theta )$ when:
$\theta = {90^ \circ }$
$\theta = {45^ \circ }$. Give an exact answer.
$\theta = {30^\circ}$. Give an exact answer.
$\theta = {57^\circ}$
$\theta $ is some measure between ${0^\circ}$ and ${90^\circ}$. (Your answer should be expressed in terms of $\theta $.)
For values of ${\theta ^{}}$ between ${0^\circ}$ and ${90^\circ}$, how are $\cos \theta $ and $P(\theta )$ related?
Now, let’s consider angles greater than ${90^\circ}$.
Calculate $P(150^\circ)$, with P being the same position function as in question 4.
What is $P(253^\circ)$?
Compare these values to the sine and cosine of $150^\circ$ and $253^\circ$.
Using the diagram and your calculations, what do you think the tangent of $253^\circ$ is? The tangent of $150^\circ$? Check them on your calculator.
It is the convention for rotations that motion in a counterclockwise direction is considered positive, while motion in a clockwise direction is considered negative. So if our wheel is spun $57^\circ$ counterclockwise we would input $57^\circ$ in our function $P(\theta )$, as we did in problem 1, but if our wheel is spun $57^\circ$ clockwise we would input $–57^\circ$ in our function $P(\theta )$. So the output for would be the coordinates of the pin after the wheel is spun $57^\circ$ clockwise.
Find:
$P( - 240^\circ )$. Give an exact answer.
$P( - 2640^\circ )$. Give an exact answer.
$P( - 237^\circ )$.
$\tan ( - 237^\circ )$.
$P( - \theta )$, where $0^\circ < \theta < 90^\circ $. (Your answer should be expressed in terms of $\theta $.)
Now define sine, cosine, and tangent of ${\theta ^{}}$ for every value of ${\theta ^{}}$.
For angles between 0 and 90 degrees, is using your definition in problem 7 equivalent to using your definition in problem 1? Why or why not?
$P(46280^\circ ) = ( - 0.94, - 0.34)$. Without using the cosine button on your calculator, find the cosine of $44480^\circ $.
Let $\cos \theta = - 0.4$.
For how many angles is that true?
How many of these angles are between $–180^\circ$ and $360^\circ$?
With the help of your calculator find all the angles in part b.
Assuming that $\cos 80^\circ = 0.17$, use the symmetry of the circle to find $\cos 100^\circ $, $\cos ( - 260^\circ )$, $\cos 260^\circ $, $\cos 280^\circ $, $\sin 190^\circ $, and $\sin ( - 10^\circ )$.
Let’s revisit question 4, but with a wheel of radius 7 feet instead of 1 foot. The wheel is still centered at $(0,0)$, and still with a pin at $(7,0)$. Let $Q(\theta )$ be the function which outputs the coordinates of the pin after this larger wheel has been spun an angle ${\theta ^{}}$ in a counterclockwise direction.
What is $Q(48^\circ )$?
What is $Q(109^\circ )$?
How would you define sine and cosine of ${\theta ^{}}$ using this $Q(\theta )$ function? How would you define tangent?
How would you define sine, cosine, and tangent using a circle of radius $r?$
In the diagram below, there is a circle of radius 2 inches, with radii drawn at ${15^\circ}$ intervals.
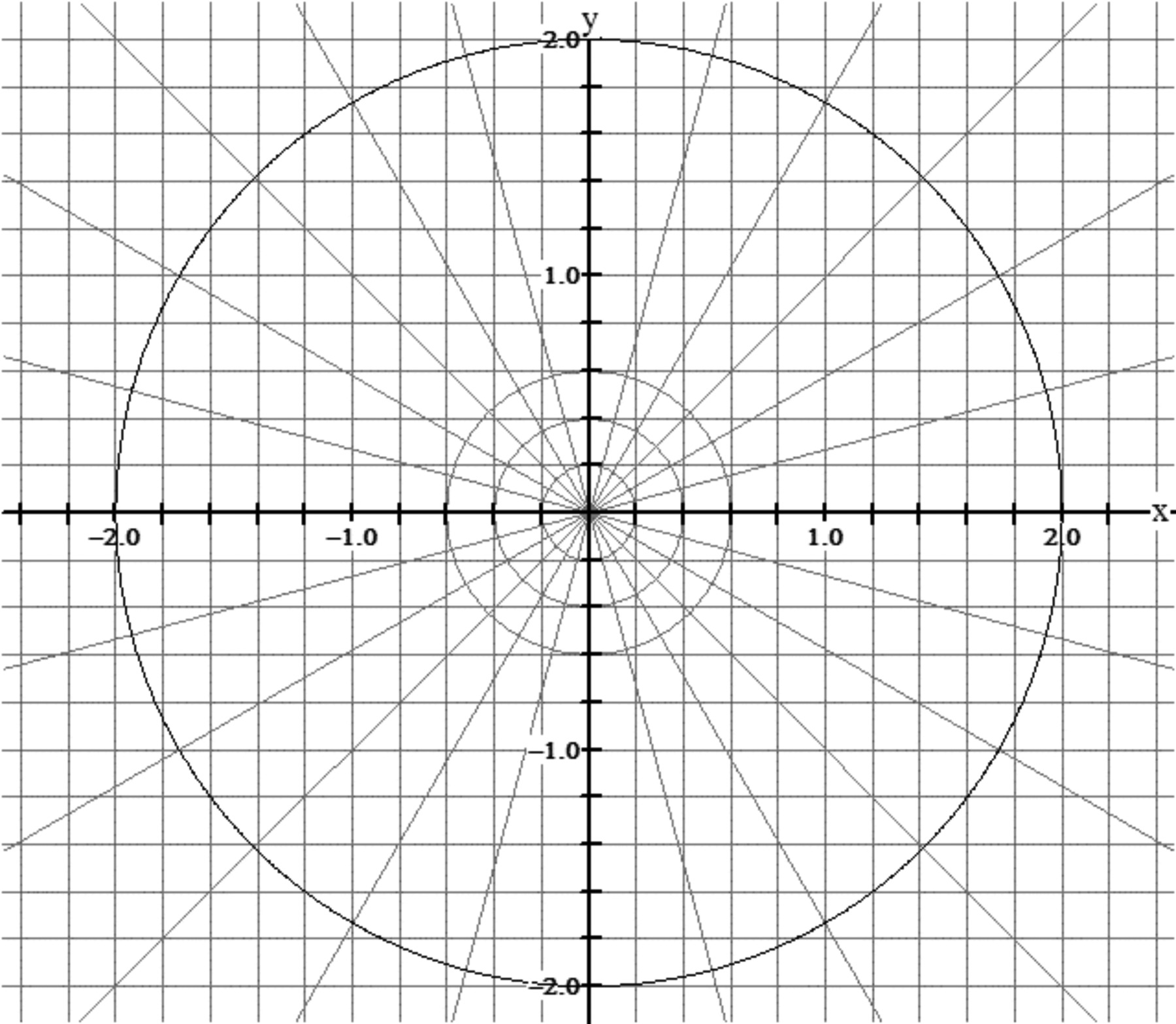
Use careful estimates and the conclusion of problem 12 to calculate the sines of ${30^\circ}$, ${60^\circ}$, ${90^\circ}$, $120^\circ $, ..., ${360^\circ}$.
Using your calculations in part a, sketch a graph with $\theta $ on the horizontal axis and $\sin \theta $ on the vertical axis. (Use values of $\theta $ from $- {360^\circ}$ to ${360^\circ}$.)
Surprise! There are actually three more trigonometric ratios (functions) in addition to the three you already know. Here are their names and definitions:
Cosecant of angle $\theta $, written $\csc \theta $, is defined thus: $\csc \theta = \frac{r}{y}$
Secant of angle $\theta $, written $\sec \theta $, is defined thus: $\sec \theta = \frac{r}{x}$
Cotangent of angle $\theta $, written $\cot \theta $, is defined thus: $\cot \theta = \frac{x}{y}$
Use the unit circle to find $\csc \theta $, $\sec \theta $ and $\cot \theta $ for $\theta = 240^\circ$.
Practice
Use the symmetry of the circle to complete the following chart. Give exact answers. Copy the chart into your notebooks.
|
$\theta $ |
30° | 45° | 60° | 315° | –210° | 210° | –315° | 150° | 240° |
| $\sin \theta $ | |||||||||
| $\cos \theta $ | |||||||||
| $\tan \theta$ |
(For this problem use the circle of problem 13.)
Use careful measurements and the conclusion of problem 7 to calculate the cosines of ${30^\circ}$, ${60^\circ}$, ${90^\circ}$, etc.
Using your calculations in part a, sketch a graph with $\theta $ on the horizontal axis and $\cos \theta $ on the vertical axis. (Use values of $\theta $ from $- {360^\circ}$ to ${360^\circ}$.)
Determine, without using your calculator, which of the following expressions are the same as $\sin {27^\circ}$.
$\sin {({180^\circ} - {27^\circ})^{}}$, $\sin {({180^\circ} + {27^\circ})^{}}$, $\sin {( - {27^\circ})^{}}$, $\sin {({360^\circ} + {27^\circ})^{}}$, $\sin (-207^\circ)$
Find, without using your calculator, two of the following expressions which are the same.
$\sin {27^\circ}$, $\cos {27^\circ}$, $\sin(-153^\circ)$, $\cos(-153^\circ)$, $\cos 63^\circ$
Find at least two values for $\theta $ that fit the equation $\sin {\theta ^\circ}$=$\dfrac{{\sqrt 3 }}{2}$. How many such values are there?
Problems
At constant speed, a wheel rotates once counterclockwise every 8 seconds. The center of the wheel is $(0,0)$ and its radius is 1 foot. A pin is initially at $(1,0)$. Where is it 69 seconds later?
A wheel whose radius is 1 is placed so that its center is at $(3,2)$. A pin on the rim is located at $(4,2)$. The wheel is spun $\theta $ degrees in the counterclockwise direction. Now what are the coordinates of that pin? Does your answer work for 90 degrees? 180 degrees?
For the following equations use a circle of radius 2 (and your calculator for part b only) to find all solutions $\theta $ between ${0^\circ}$ and ${360^\circ}$:
$\cos \theta = - \dfrac{{\sqrt 3 }}{2}$
$\tan \theta = 6.3138$
$\sin \theta = - \dfrac{{\sqrt 2 }}{2}$
$\cos \theta = \cos ({251^\circ})$
$\sin \theta = \sin {580^\circ}$
${(\tan \theta )^2} = 3$
Find all solutions $t$ between ${360^\circ}$ and ${720^\circ}:$
$\cos t = \sin t$ (no calculator)
$\sin t = - 0.9397$
$\cos t < \dfrac{{\sqrt 3 }}{2}$ (no calculator)
In the next few problems you are asked to come up with conjectures or to examine the validity of various statements. You might want to see if the conclusion reached is even plausible, by looking at specific, easy-to-check cases. A simple check will either give the conclusion credence (and thus makes it worth trying to prove) or disprove it instantly.
Asked to simplify the expression $\sin ({180^\circ} - \theta )$, Alex volunteered the following solution: $\sin ({180^\circ} - \theta ) = \sin {180^\circ} - \sin \theta $, and, because $\sin {180^\circ}$ is zero, it follows that $\sin ({180^\circ} - \theta )$ is the same as $- \sin \theta $.
Is this conclusion plausible?
If it is plausible, try to prove the result. If it isn’t, can you come up with a correct way to express $\sin ({180^\circ} - \theta )$ in simpler form?
Answer the same questions for $\cos ({180^\circ} - \theta )$.
Find simpler, equivalent expressions for the following: $\sin ({180^\circ} + \theta )$, $\cos ({180^\circ} + \theta )$, $\tan ({180^\circ} + \theta )$, $\cos ({360^\circ} - \theta )$, $\sin ({360^\circ} - \theta )$, $\tan ({360^\circ} - \theta )$, $\cos ({360^\circ} + \theta )$, $\sin ({360^\circ} + \theta )$, $\tan ({180^\circ} - \theta )$, $\tan ({360^\circ} + \theta )$
Is it the case that $\sin ({90^\circ} - \theta ) = \cos \theta $ ? Explain. Then write simpler, equivalent expressions for $\cos ({90^\circ} - \theta ),\,\,\sin ({90^\circ} + \theta ),\,\,\cos ({90^\circ} + \theta )$.
Is $\sin ( - \theta )$ always the same as $- \sin (\theta )$? What can be said about $\cos ( - \theta )$?
Do the following problems without using a calculator. Explain your reasoning.
Which is larger: $\cos {311^\circ}$ or $\cos {312^\circ}$?
Which is larger: $\sin {311^\circ}$ or $\sin {312^\circ}$?
If $\sin A$ is known to be 0.96, then what is $\cos A$? What if it is also known that $A$ is an obtuse angle?
Hendrickson is thinking of an angle $\theta $ where $\tan \theta > \sin \theta $, and also where $\sin \theta < \cos \theta $. Give two possible values for $\theta $ that are in different quadrants.
Rodney is running around the circular track ${x^2} + {y^2} = 10000$, whose radius is 100 meters, at 4 meters per second. Rodney starts at the point $(100,0)$ and runs in the counterclockwise direction. After 30 minutes of running, what are Rodney’s coordinates? Copyright Phillips Exeter Academy
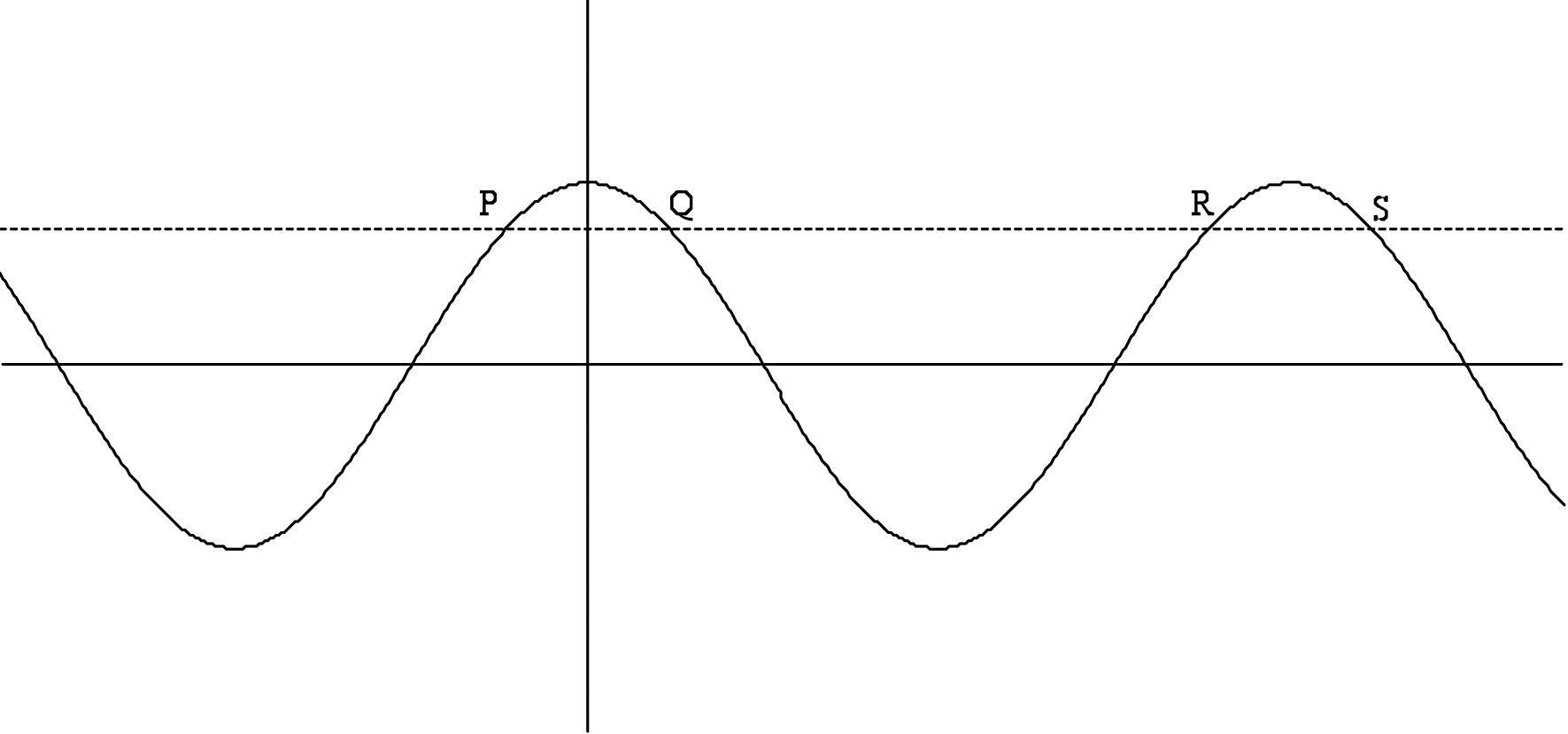
Below are the graphs of $y = \cos x$ and $y = 0.7431$ (dotted). Given that $Q=(42, 0.7431)$, find coordinates for the intersection points P, R, and S without using a calculator. Use a calculator to check your answers. Copyright Phillips Exeter Academy
For how many angles in the first quadrant will $\sin \theta $ be rational?
One way to find the sine of a 60 degree angle is to draw a circle of radius 2 and draw the related
Choose an angle $\theta $ and calculate ${(\cos \theta )^2} + {(\sin \theta )^2}$. Repeat with several other values of $\theta $. Explain the results. (Note that it is customary to write ${\cos ^2}\theta + {\sin ^2}\theta $ instead of ${(\cos \theta )^2} + {(\sin \theta )^2}.)$
For any angle $\theta $, is it true that $1 + {\tan ^2}\theta = {\sec ^2}\theta $ ? If so, prove it. If not, produce a counterexample.
Asked to find an expression that is equivalent to $\cos(\alpha + \beta)$, Laura responded $\cos (\alpha ) + \cos (\beta )$. What do you think of Laura’s answer, and why?
On your calculator, draw a graph of the function $y = \tan x$ with ${0^\circ} < x < {360^\circ}$. Something appears to be wrong here. Say what you think is wrong and explain what’s going on.
Solve the following without finding the angle $\theta $.
Given that $\sin \theta = \frac{{12}}{{13}}$, with ${0^\circ} < \theta < {90^\circ}$, find the values of $\cos \theta $ and $\tan \theta $.
Given that $\cos \theta = \frac{7}{{25}}$, with ${270^\circ} < \theta < {360^\circ}$, find $\sin \theta $ and $\tan \theta $.
Suppose that $\csc \theta = -\frac{{
25}}{7}$ and
The point $P( - 12,16)$ is on a circle whose center is the origin. Find the cosine of angle $\theta $, the angle between the positive $x$-axis and the radius to $P$.
The point $P$ is on a circle whose center is the origin, and the $x$-coordinate of $P$ is five times its $y$-coordinate. Find the cosine of angle $\theta $, the angle between the positive $x$-axis and the radius to $P$.
Is it possible for $\sin \theta $ to be exactly twice the size of $\cos \theta $ ? If so, find such an angle $\theta.$ If not, explain why not.
Find the three smallest positive solutions to ${2\sin \theta} = {–1.364}$.
Don’t use a calculator for this problem.
Reduce: $\dfrac {{5ab}-{10bc}} {ab}$
Reduce: $\dfrac {{3x^2}-{24}} {3x}$
Solve for $x$: $2{x^2} - 3x - 2 = 0$
Add: $\dfrac{7}{4} + \dfrac{{3a}}{b}$
Subtract: $\dfrac {x} {4} - \dfrac {x-1} {2}$
Find all the solutions $x$, given ${0^\circ} ≤ {x} < {360^\circ}$ .
$(\cos x - .5)(\sin x + \dfrac{{\sqrt 3 }}{2}) = 0$
${(\cos x)^2} - 5\cos x + 4 = 0$
$3{(\tan x)^2} + 5\tan x = 0$
$2{(\sin x)^2} + \sin x = 3$
Exploring in Depth
Paul rides a Ferris wheel for five minutes. The diameter of the wheel is 10 meters, and its center is 6 meters above the ground. Each revolution of the wheel takes 30 seconds. Paul's fear of heights kicks in when he is more than 9 meters above the ground. For how many seconds does Paul feel uncomfortable?
Jasper’s bike has wheels that are 27 inches in diameter. After the front wheel picks up a tack, Jasper rolls another 100 feet and stops. How far above the ground is the tack?
You have a circular dartboard. Its target area is defined in an unusual way. Take any point within the dartboard. Draw a straight line that goes through this point and the center of the board. Measure the angle this line makes with the line going from the center to the “easternmost” point on the dart board. If the tangent of this angle is between -0.2 and 0.6, then the point is shaded. Otherwise, it is not shaded. What are your chances of hitting this target area?
Given that $\sin \theta = k$, and that ${0^\circ} < \theta < {90^\circ}$, find expressions for $\cos \theta $ and $\tan \theta $.
What do the graphs of $y = \sin x$ and $y = \sin 2x$ have in common, and how do they differ? How about the graphs of $y = \cos x$ and $y = \cos mx$, where $m$ is any positive integer?
Starting at the same spot on a circular track that is 80 meters in diameter, Andy and Brandon run in opposite directions, at 300 meters per minute and 240 meters per minute, respectively. They run for 50 minutes. What distance separates Andy and Brandon when they finish? Interpret the word distance any way you wish. Copyright Phillips Exeter Academy