Introduction
The Leaning Tower of Pisa

The Leaning Tower of Pisa has been leaning almost since the onset of construction in 1173. From ground to top, the tower is 183.27 ft along the lowest side and 186.02 ft along the highest side. The angle of slant of the tower—formed by its shorter slant height and the ground—is ${95.5^ \circ }$. An apocryphal tale states that Galileo Galilei (1564-1642), an Italian physicist, mathematician, and philosopher, dropped two cannon balls of different weights from the top of this leaning tower in trying to demonstrate that the descending speed of a falling body is independent of its weight.
What is the distance traveled by an object dropped from the top of the Tower of Pisa, on its lowest side, when it hits the ground?
What is the horizontal distance from the point where the object hits the ground to the base of the tower?
The Tower of Pisa first acquired a slant after the third floor was built in 1178. More recently, in 1990, it was closed to the public because of safety fears. In fact, the tower was on the verge of collapse, and it was projected that it would have collapsed between 2030 and 2040. However, it has been straightened a bit, but still remains slanted (the tower has been reopened to the public). Thus, the angle of slant of the Tower of Pisa, $\alpha $, has been changing for centuries. The following is a sketch of the situation.

In trying to determine a general expression for the distance, $h$, traveled by an object dropped from the top of the Tower of Pisa’s lowest side when it hits the ground (assuming that the shorter length of the tower has not changed), Gerald found the following expression.
For the horizontal distance from the point where the object hits the ground to the base of the tower, Gerald found the following expression.
Do you agree with these statements? Explain your answer.
You have no more than two seconds after reading the statement of this problem to solve it.
What is the value of ${\sin ^2}\left( {\dfrac{{\sqrt[7]{{123456}}}}{{\pi + 13}}} \right) + {\cos ^2}\left( {\dfrac{{\sqrt[7]{{123456}}}}{{\pi + 13}}} \right)$?
Development
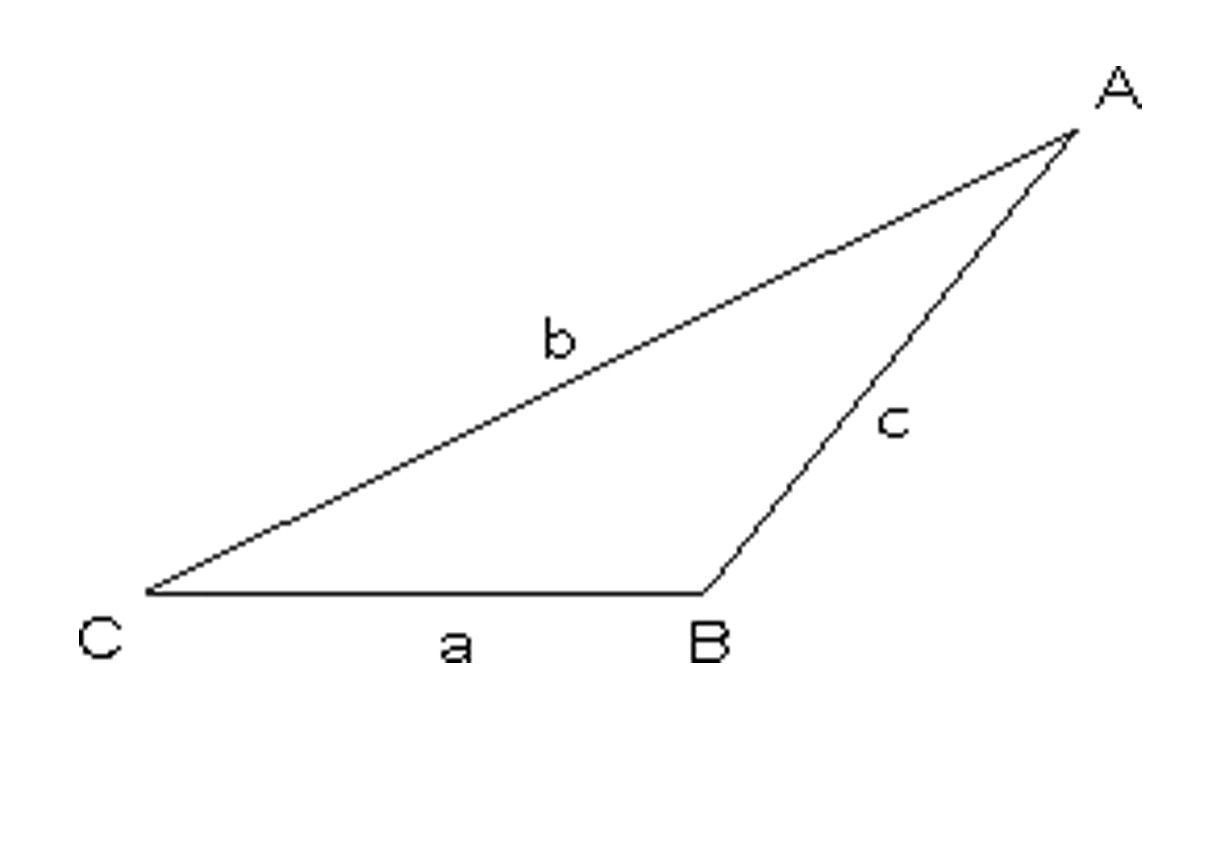
We follow the convention of labeling the angles of a triangle using capital letters, and the lengths of the corresponding opposite sides with the corresponding lower-case letters. For example, we may label A, B, C the angles of the triangle, and a, b, c the corresponding opposite sides, as in the figure below.
The Bermuda Triangle
The “Bermuda Triangle” or “Devil’s Triangle” is an imaginary area located off the southeastern Atlantic coast of the United States of America, which is noted for a supposedly high incidence of unexplained disappearances of ships and aircraft. The vertices of the triangle are generally believed to be Bermuda, Miami (Florida), and San Juan (Puerto Rico).

One of the amazing stories from this triangle tells that an aircraft (A in the figure below) was 747.23 miles from the airport of Miami (M in the figure), on the line joining Miami and Bermuda, when its crew received an SOS signal from Cyclops (C in the figure), a ship located at a point on the line joining Miami airport and San Juan, which was sinking. Flight controllers at the airport were able to estimate the measure of $\angle AMC$ to be ${52^ \circ }$.

Based on the previous story, Mr. Thomas Howard designed a problem for his mathematics class. The initial situation described in the story, however, contained more than the minimal information required to solve the problem; therefore, he divided the class into two groups, Group I and Group II, and gave each group a problem with different pieces of information, but the same goal to determine how many miles the aircraft had to travel through the purportedly dangerous Bermuda Triangle before reaching Cyclops.
Group I: Besides the general information described above, it is known that $m\angle C = {60^ \circ }$. What is the distance between the aircraft A and the sinking ship Cyclops C? Find a solution to this problem and explain how you arrived at your answer.

Group II: Besides the original and general information, it is known that the distance from Cyclops to the airport of Miami is 800 miles, as shown in the figure below. What is the distance between the aircraft A and the sinking ship Cyclops C? Find a solution to this problem and explain how you arrived at your answer.

In Problem 5, if the distance given were m and the one to be found were c, the problem could be solved in a similar way. Consider the more general triangle below.
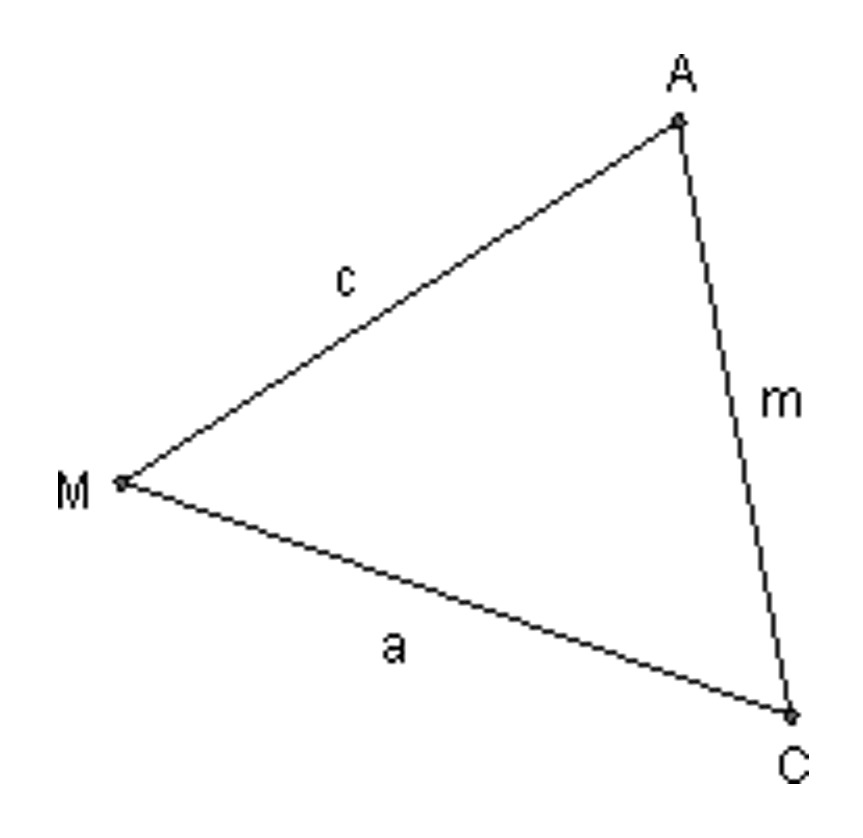
Draw the altitude from A to side $\overline {MC} $, and prove that ${\dfrac {c} {\sin C}} = {\dfrac {m} {\sin M}} \;$.
Hint: If $h$ is the length of the altitude from A to $\overline {MC} $, find h in $\Delta {ADM}$ in terms of $c$ and $\angle M$. Then find $\sin C$ in $\Delta {ADC}$.
Now, prove that ${\dfrac {m} {\sin M}} = {\dfrac {a} {\sin A}} \;$
In group II, Rebecca noticed that if the measure of $\angle M$ were ${90^ \circ }$ rather than ${52^ \circ }$, the Pythagorean Theorem would guarantee that ${m^2} = {a^2} + {c^2}$. “However,” she said, “since $\angle M$ is less than ${90^ \circ }$, the Pythagorean relationship among $m$, $a$, and $c$ must be adjusted.” This adjustment is the result that you are about to find in Part c of the following problem.
Consider the triangle in Mr. Howard’s problem in a more general form, as shown below, and prove the following.

$h = c\sin M$
${y} = {a-{c\cos M}}$
${m^2} = {c^2}{\sin ^2}M + {\left( {a - c\cos M} \right)^2}$
In part c of the previous problem, expand the square on the right side of the equality. Then use the trigonometric identities that you have learned thus far to find an expression as simple as possible relating $m$ to $c$, $a$, and $\angle M$.
As announced above, the expression relating $m$ with $c$, $a$, and $\angle M$ that you may have found in the previous problem is the adjustment to the Pythagorean relationship ${m^2} = {a^2} + {c^2}$ required when $m\angle M < {90^ \circ }$. In a similar way, adjustments to the Pythagorean relationship relating $a$ to $m$ and $c$ as well as to that relating $c$ to $a$ and $m$ may be needed when either $m\angle A$ or $m\angle C$ is not ${90^ \circ }$, as in the case illustrated above.
Consider the general triangle shown below.
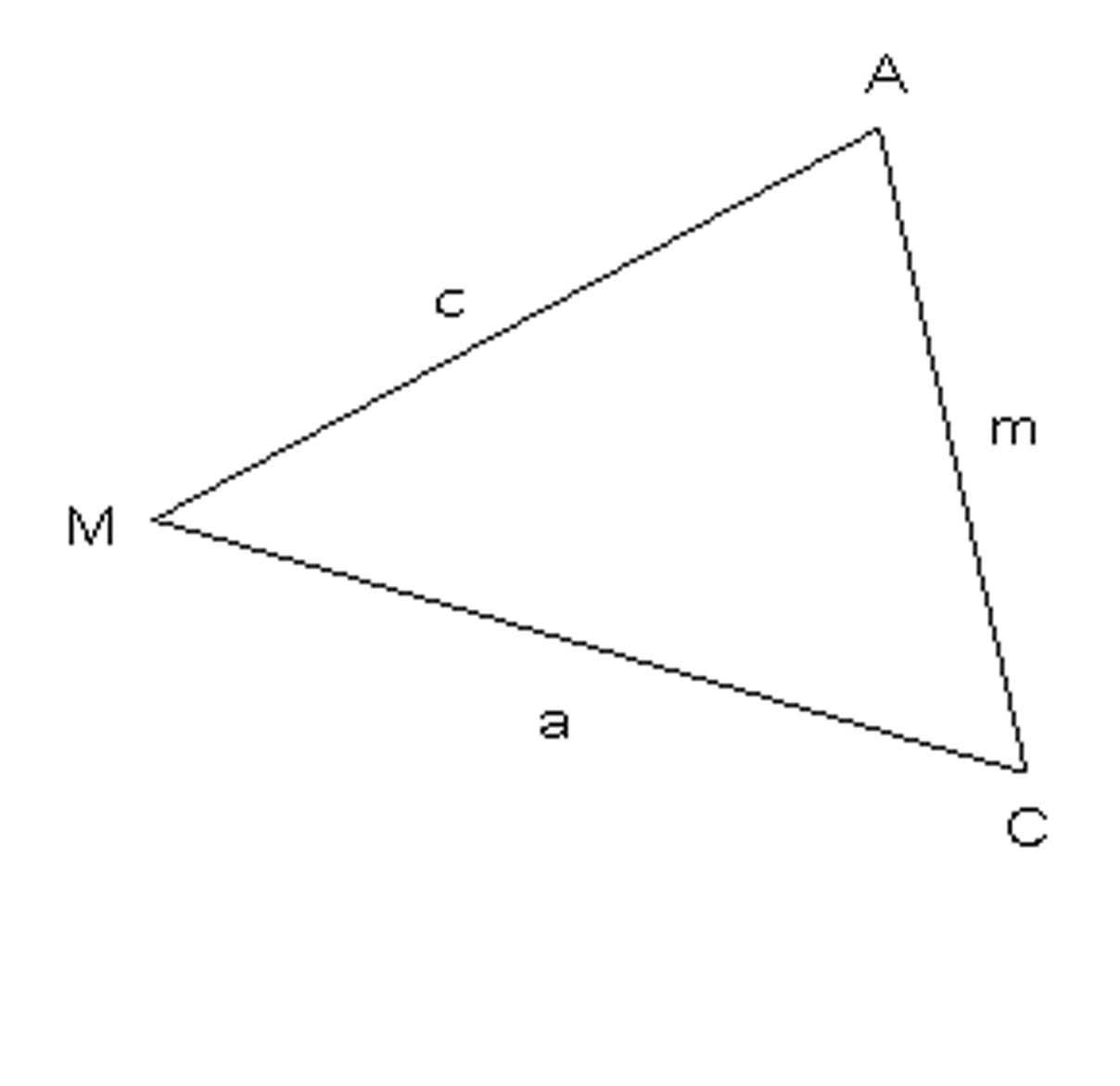
If $m\angle A = {90^ \circ }$, how would $a$ be related to $m$ and $c$?
Conjecture an adjustment to the Pythagorean relationship in part a that may be required when $m\angle A \ne {90^ \circ }$. Would the proof of your conjecture in this case be quite different from that developed in Problems 8 and 9? Explain.
If we had that $m\angle C = {90^ \circ }$, how would $c$ be related to $a$ and $m$?
Conjecture an adjustment to the Pythagorean relationship in part c that may be required when $m\angle C \ne {90^ \circ }$. Would the proof of your conjecture in this case be quite different from that required in Part b? Explain.
Summarizing, given a triangle as the one below,

two sets of equalities have been found.
On the one hand, the set of equalities that you may have proven in Problem 7 is known as the Law of Sines.
On the other hand, the set of equalities that you may have found in Problems 9, 10b, and 10d is known as the Law of Cosines.
Practice
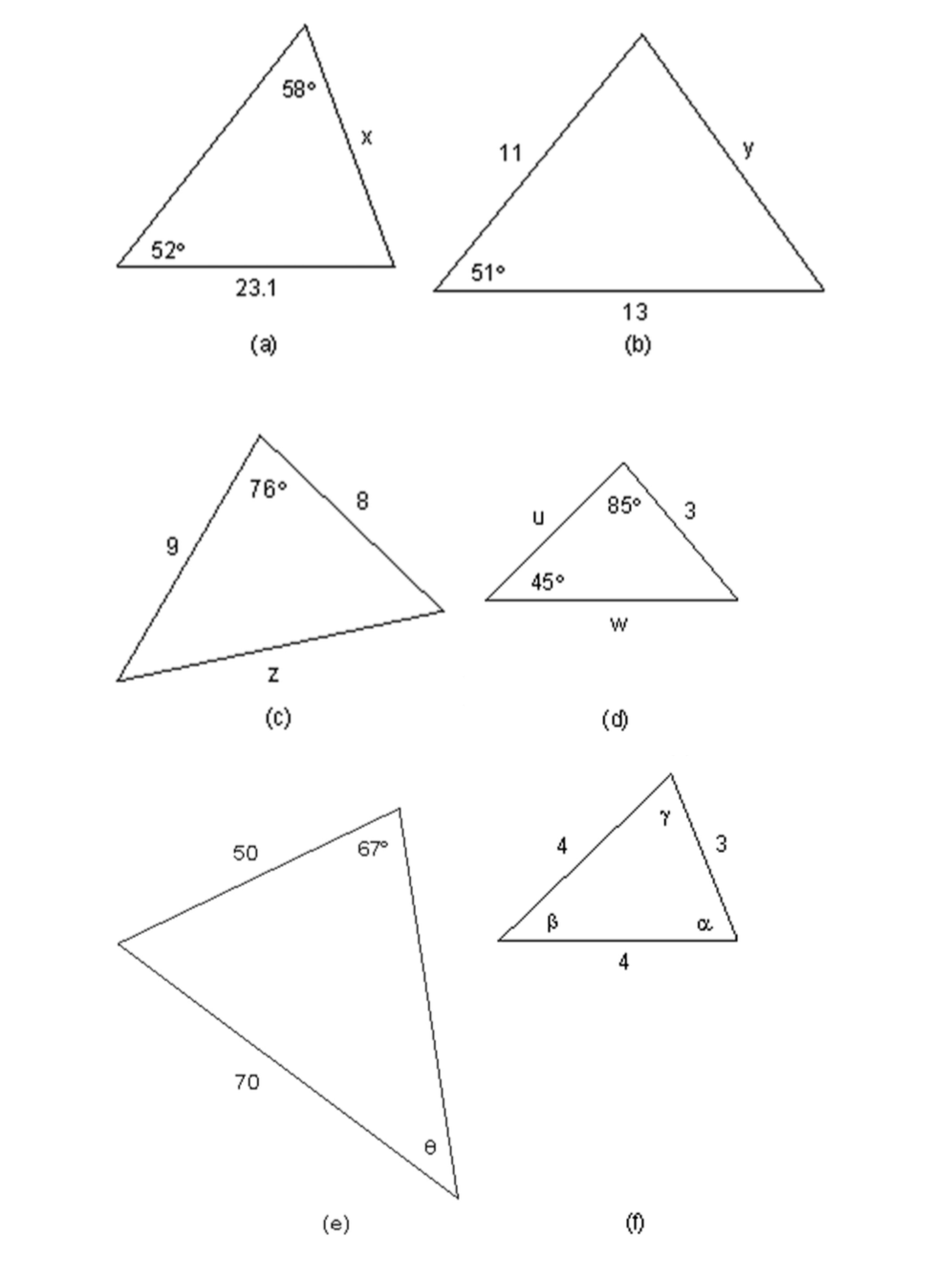
Find the indicated side lengths or angle measures in the following figures.
Further Development
When the students in Mr. Howard’s class shared their findings (the Law of Sines and the Law of Cosines) the information contained in these laws was considered “the key” to find missing side lengths or angles in any triangle, when basic information about the triangle is known. However, in reality in all the proofs only acute triangles—triangles with each of their three angles being less than ${90^ \circ }$—were used.
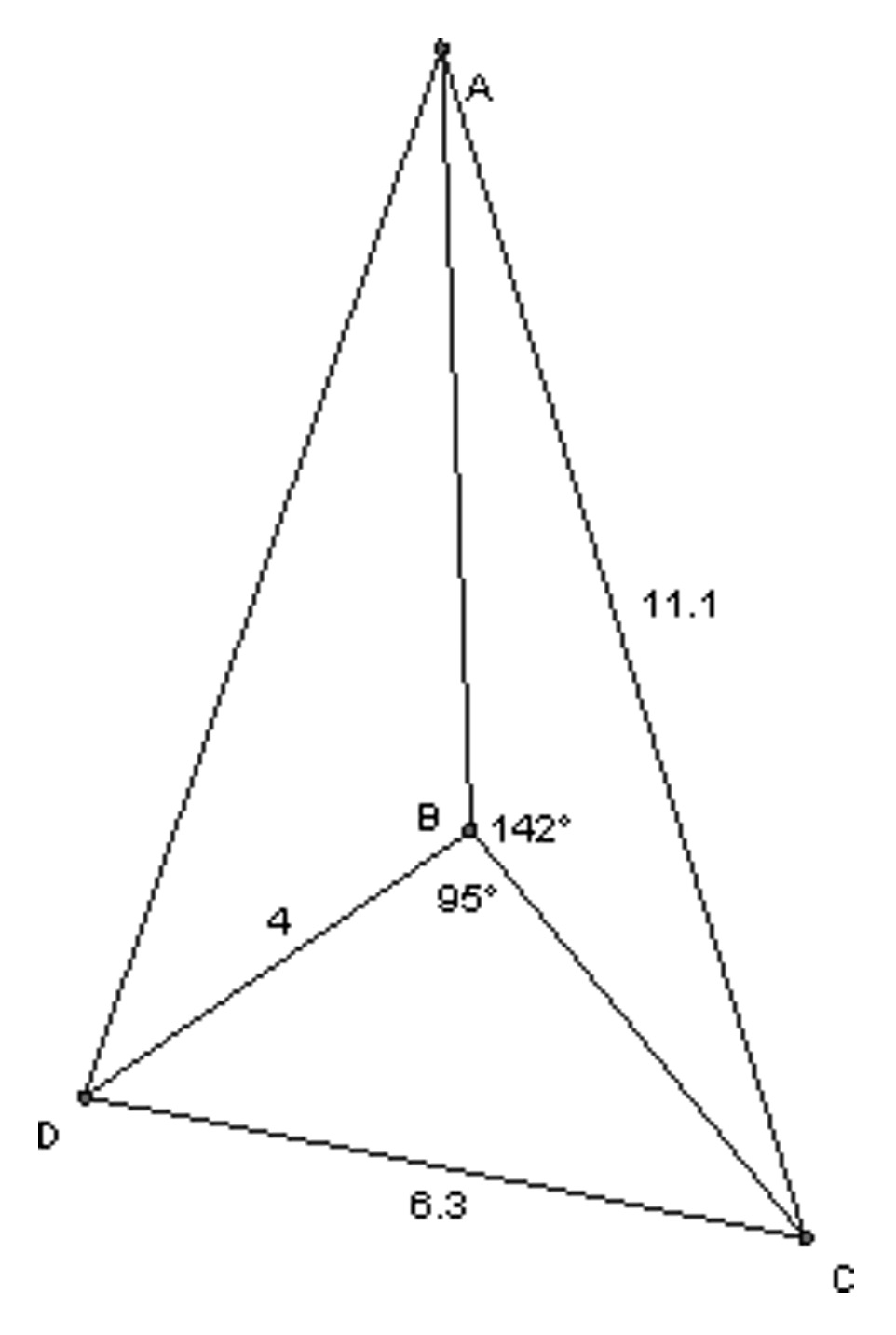
Regarding Mr. Howard’s problem, consider the following situation where $m\angle M = {142^ \circ }$.
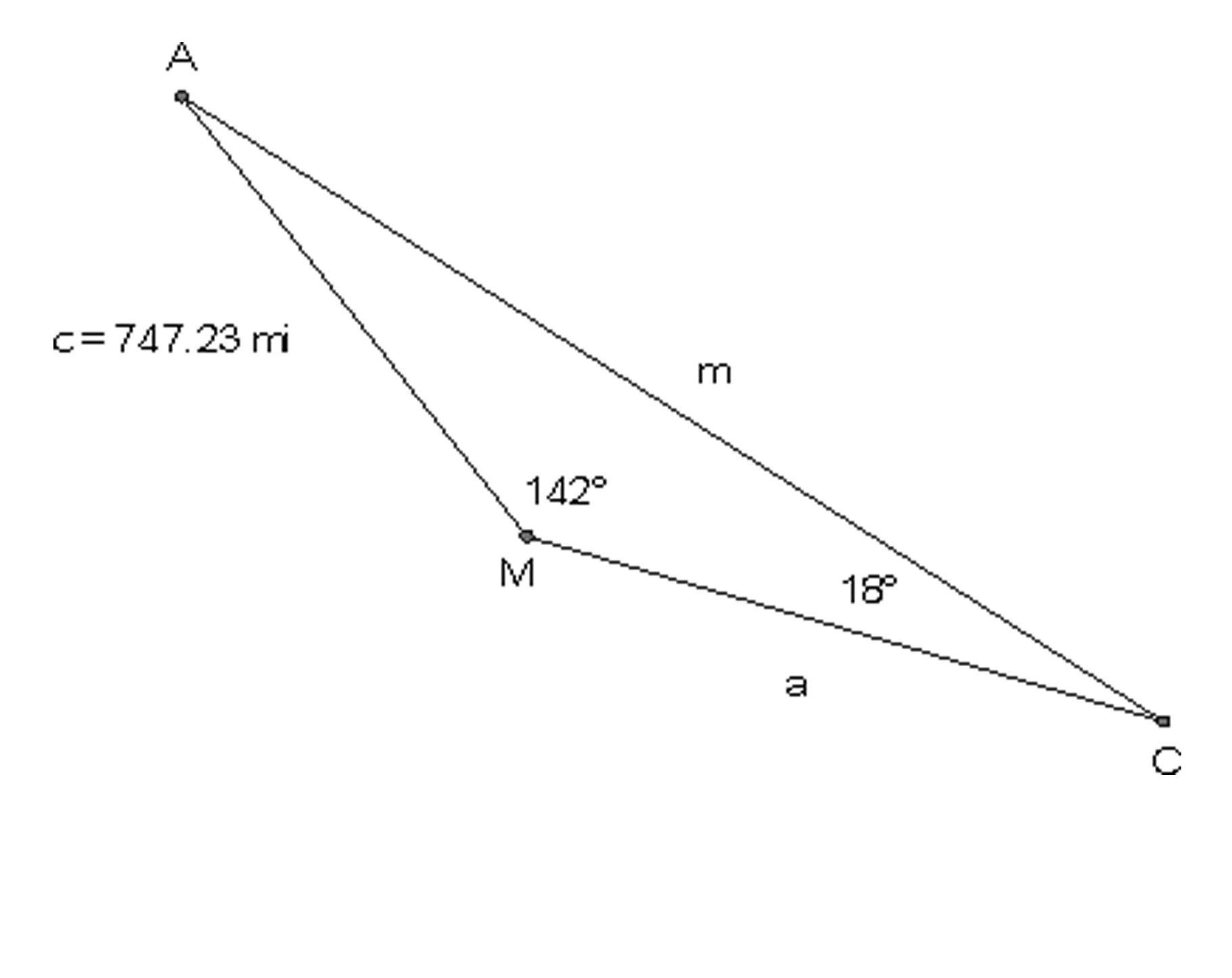
Does the proof of the Law of Sines (in Problem 7), or that of the Law of Cosines (in Problems 8 and 9), support the use of either of these laws to find $m$ in this triangle, which is not an acute triangle? Explain.
Consider the following obtuse $\Delta {AMC}$ (that is, a triangle containing an angle greater than ${90^ \circ }$).

Prove that $\dfrac{c}{{\sin C}} = \dfrac{m}{{\sin M}} = \dfrac{a}{{\sin A}}$.
Consider again the obtuse $\Delta {AMC}$. Dashed lines have been added to help you prove the equality stated in Part (a).

Prove that ${m^2} = {a^2} + {c^2} - 2ac\cos M$.
Prove that ${a^2} = {m^2} + {c^2} - 2mc\cos A$.
Prove that ${c^2} = {m^2} + {a^2} - 2ma\cos C$.
Is the Law of Sines or the Law of Cosines worth remembering? Would it be easier always to construct appropriate perpendicular lines and use only trigonometric ratios to solve the problems that may require them?
Practice
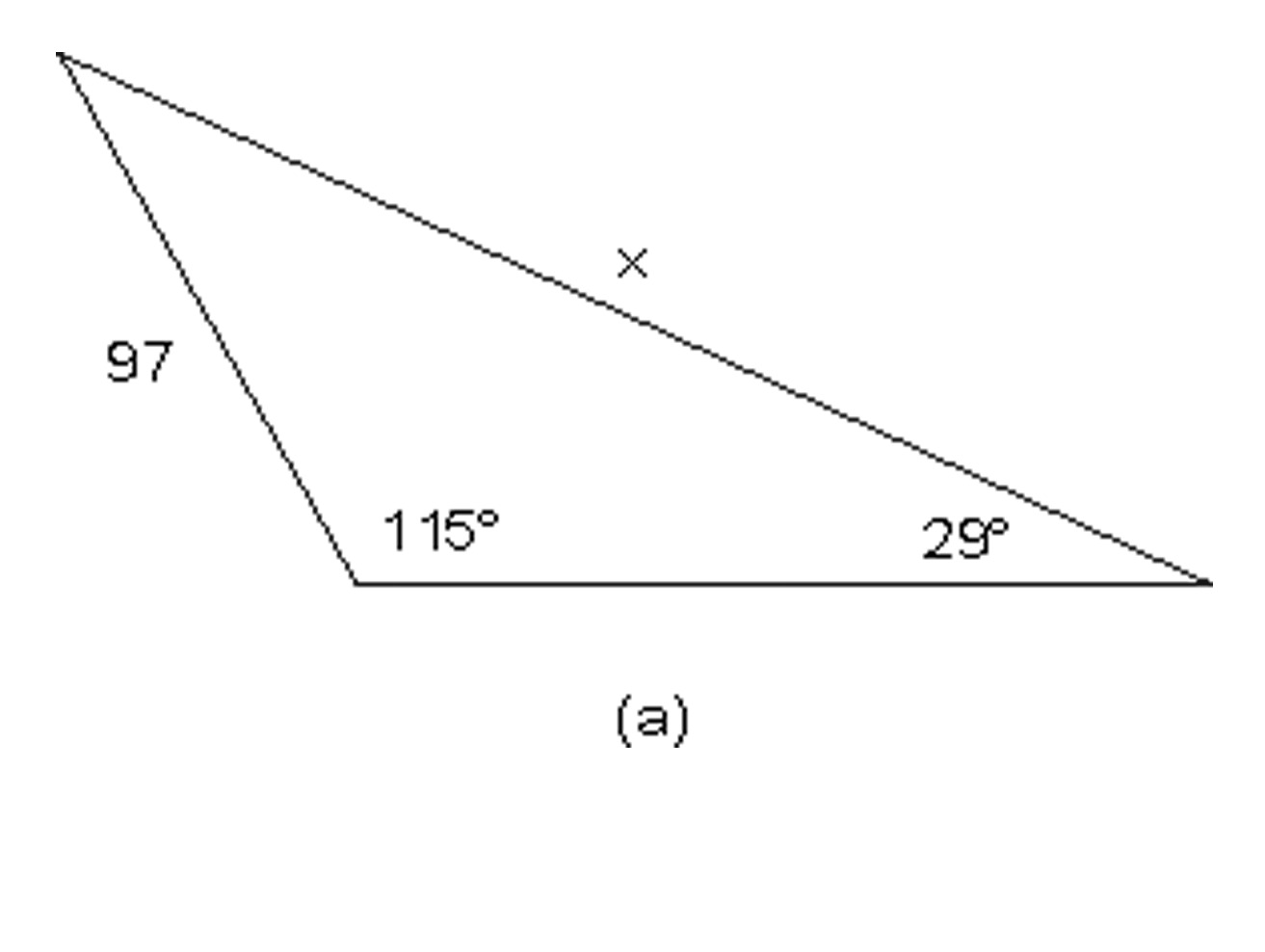
Find the indicated side lengths or angle measures in the following figures.

Two tracking stations are monitoring the path of a satellite, which has passed to the west of both stations. From station A, the angle of elevation to the satellite is 85.5 degrees. From station B, the angle of elevation to the satellite is 82 degrees. Stations A and B are 65 miles apart.

Find the distance from the satellite to tracking station A.
Find the height of the satellite above the ground.
The distance from Chicago to St. Louis is 440 km, from St. Louis to Atlanta 795 km, and from Atlanta to Chicago 950 km. What are the angles in the triangle with these three cities as vertices?
In the figure below, find the measure of angle A.
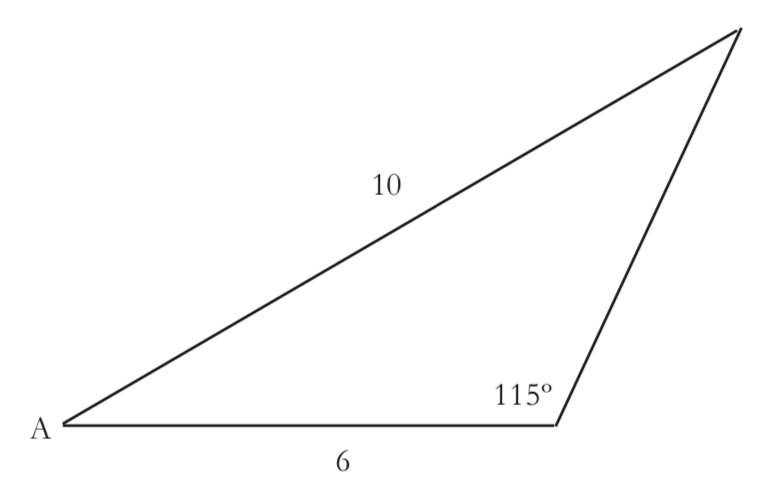
After having done these problems in the Practice section, you may be better prepared to answer question 15, repeated here:
Is the Law of Sines or the Law of Cosines worth remembering? Would it be easier always to construct appropriate perpendicular lines and use only trigonometric ratios to solve the problems that may require them?
Problems
Melissa walks along the path shown below: She goes 500 ft along a sidewalk adjacent to a field, then turns 70 degrees, walks a way across the field, and stops. Looking back, she measures a 47 degree angle between her path across the field and her line of sight to her starting point.

Find the distance that Melissa walked across the field.
How far away is Melissa from her starting point?
A sailboat is attempting to sail between two islands, 100 miles apart. From the very beginning, a wind blows the boat 15 degrees off its course. After the sailboat has been sailing for an hour and a half at 25 mph, it corrects its course so it is sailing straight toward the second island.

By how much does the sailboat need to increase its speed if it wants to arrive at its destination at the same time it would have going 25 mph along the straight path?
Find the “turn angle” – the number of degrees the sailboat needed to turn in order to correct its course.
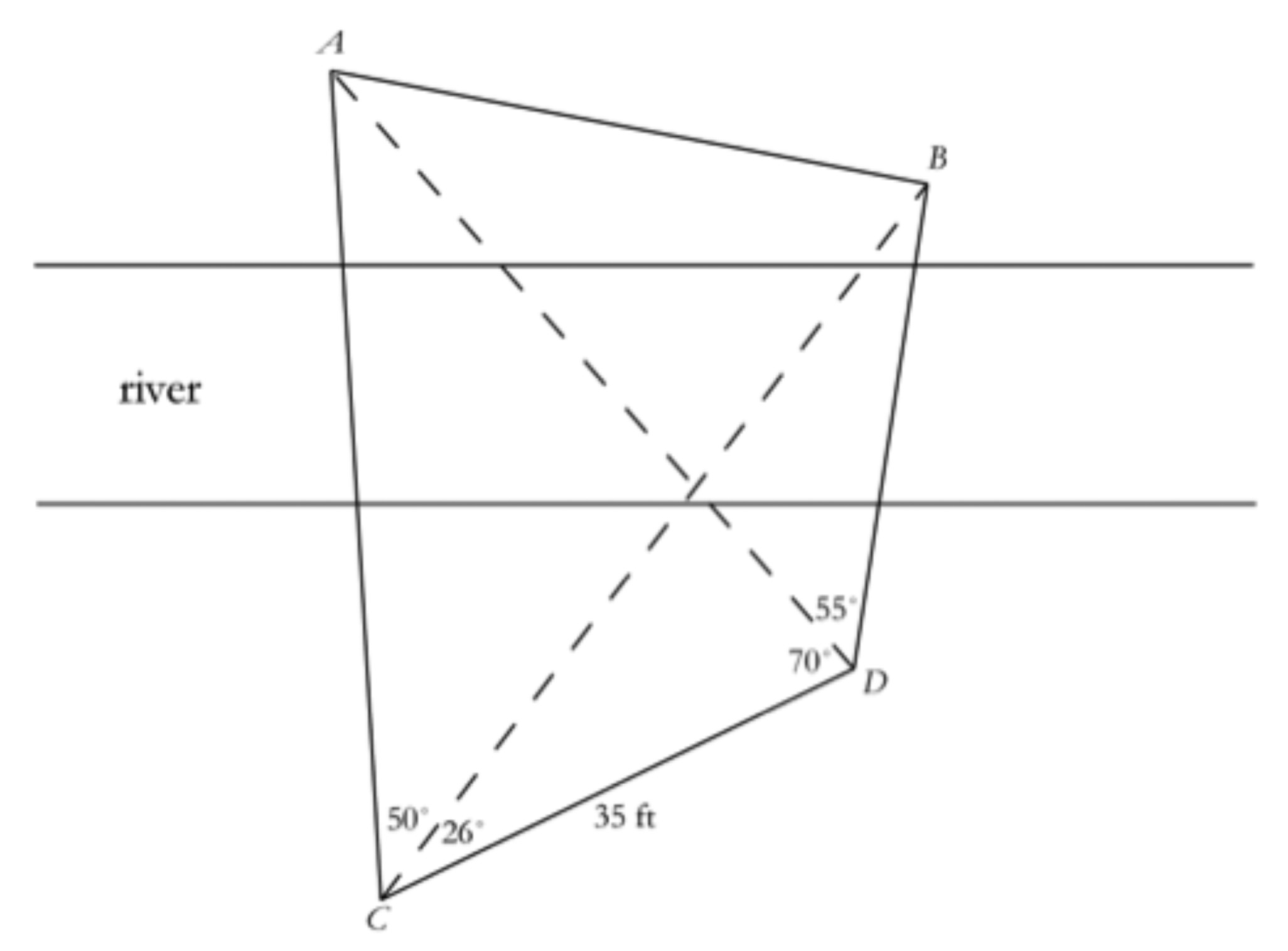
Julie needs to find the distance between two trees A and B on the opposite side of a river. On her side of the river, she chooses two points C and D, 35 feet apart. Then she measures the angles shown in the diagram. What distance between the trees will she calculate?
Find all three angles of this triangle. Check to be sure that your answer is plausible.

Find the measure of all the angles in the trapezoid.

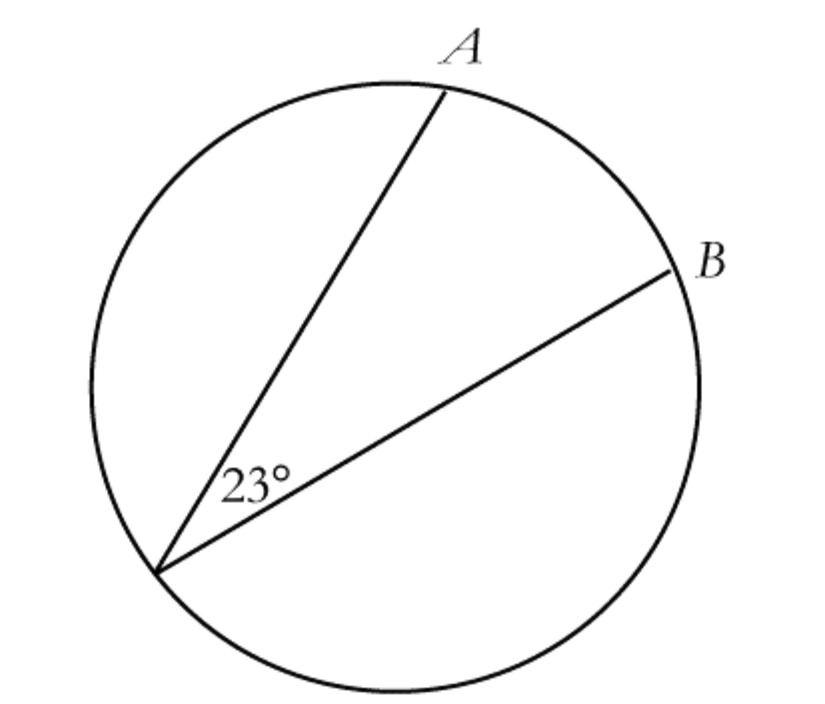
In the figure below, find X.

In the figure below, the length of the chord drawn from A is 8, and the length of the chord drawn from B is 10. Find the length of arc AB. (Hint: you will need to know the radius of the circle.)
The function ThirdSide takes an angle, theta, and outputs the third side of a triangle with sides 3 and 4 and included angle theta.
Find $Thirdside({80^ \circ })$.
What are the minimum and maximum possible values for $Thirdside(\theta )$? Justify your answer in two different ways:
- by visualizing what different triangles would look like for different values of ${\theta ^{}}$.
- by looking at the Law of Cosines formula and seeing how the value of theta affects the value of each term.
Often times, a problem that seems to be hard may be simplified a lot by just drawing a diagram or adding a couple of lines—or even just points—to a diagram already in place. These additions (to the concrete situation given) are implemented to visualize and better understand problems which may have been initially confusing. In the following problems, 29 through 33, you will have the chance to use this mathematical habit of mind repeatedly.
A triangle has a 13-inch, a 14-inch, and a 15-inch side. To the nearest tenth of an inch, how long is the median drawn to the 14-inch side? (Recall that a median is a line segment drawn from a vertex of a triangle to the midpoint of the opposite side.)
A “half-regular” pentagon isn’t perfectly regular, but it does fold perfectly in half (the left half is the same as the right half – it’s symmetric across a vertical axis). The half-regular pentagon below has a top angle of 160°, a side length of 8 for the top two sides, a side length of 9 for the base, and a total height of 14 (from the top point down to the base).

Find the area and perimeter of the pentagon.
The diagram below represents a plot of a piece of land. Find the area of the plot.

In this diagram, $\Delta {ABC}$ and $\Delta {CDF}$ are both isosceles. $AB = AC$ and $DF = DC$. $\angle E$ and $\angle EFD$ are right angles.
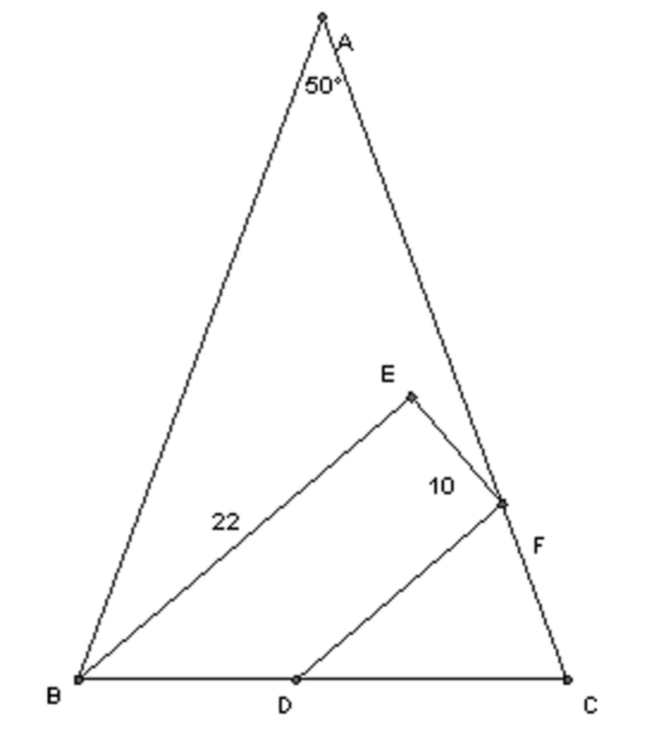
Find all the angles in the diagram.
Find $AF$.
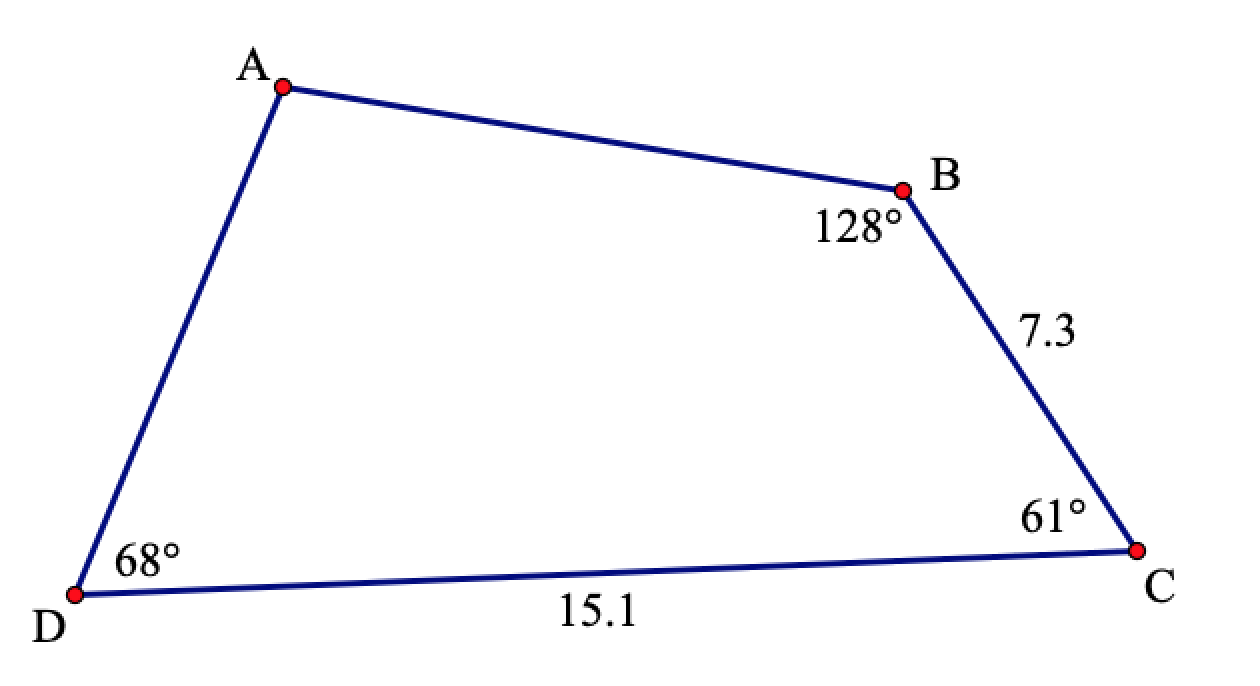
The lengths of three sides and the measure of two angles
of a quadrilateral are given, as shown in the figure
below.
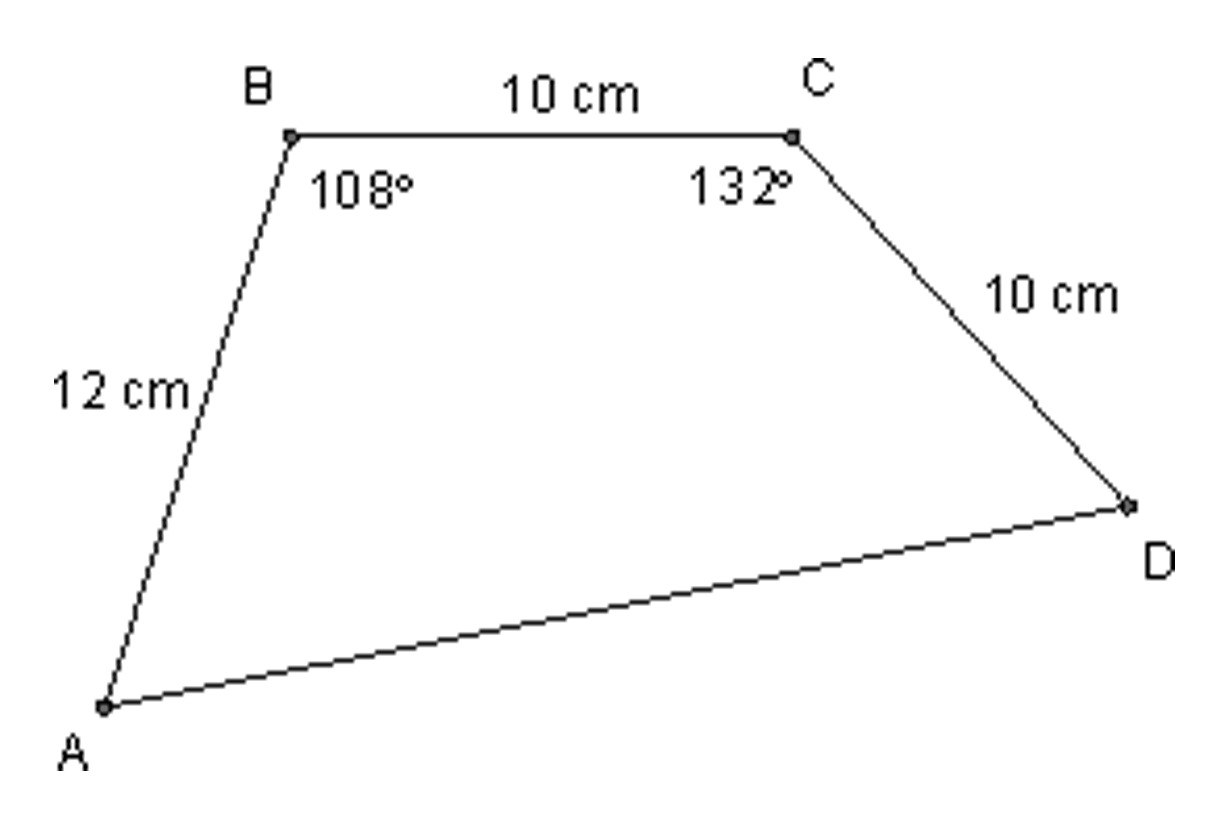
Determine the length of the diagonals of this quadrilateral. Round answers to two decimal places.
Determine the perimeter of this quadrilateral. Round the answer to two decimal places.
Determine the area of this quadrilateral. Round the answer to two decimal places.
You’re looking at the hour hand and the minute hand on a
clock at exactly 1:20. The tips of the hands are 3 inches
apart. The hour hand is 2.15 inches long. (Remember – the
hour hand is not pointing directly at the 1, since it’s
after 1:00!)
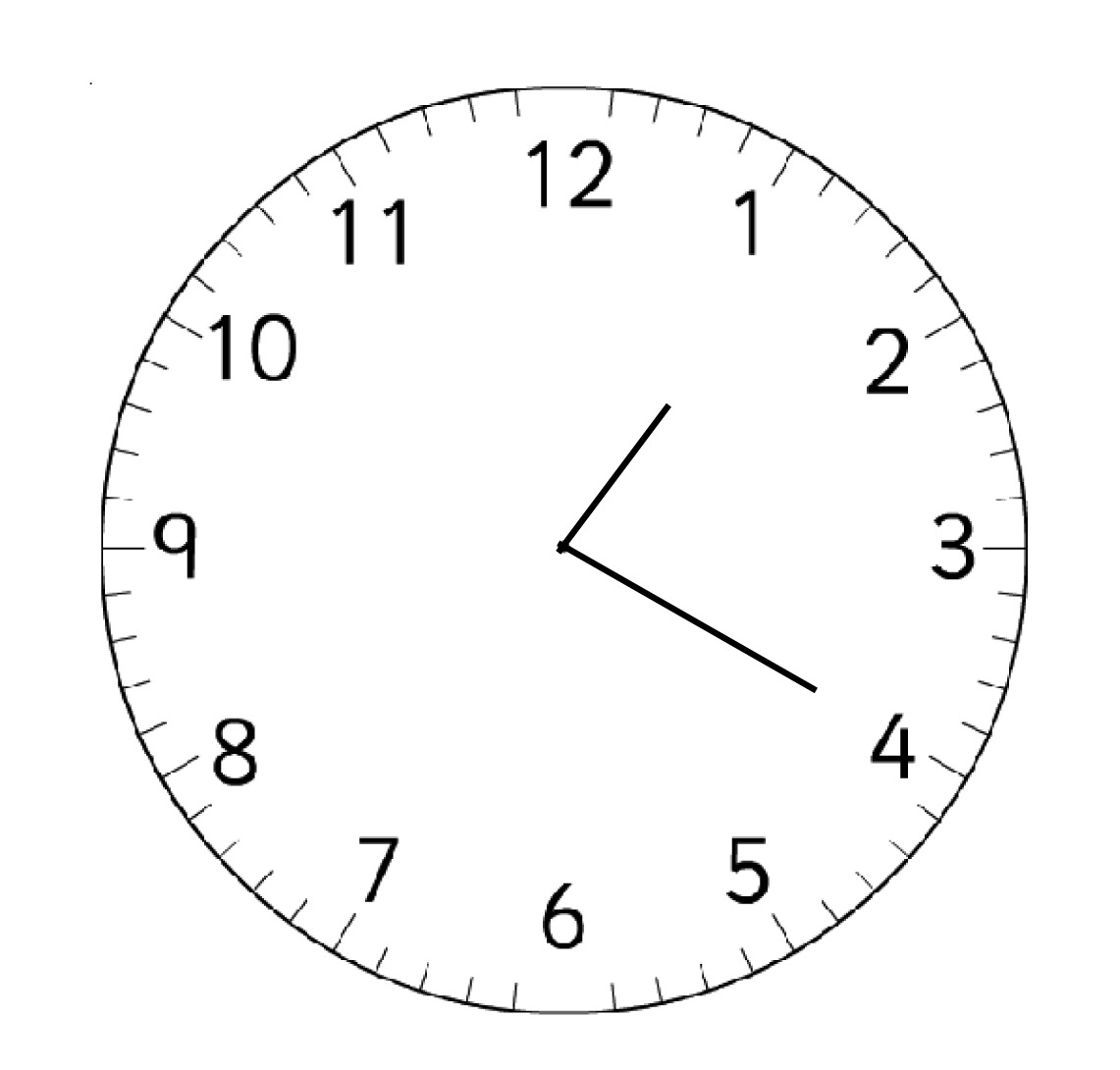
What’s the angle between the hands?
Draw the triangle that this forms, and find the other angles in the triangle.
Find the length of the minute hand.
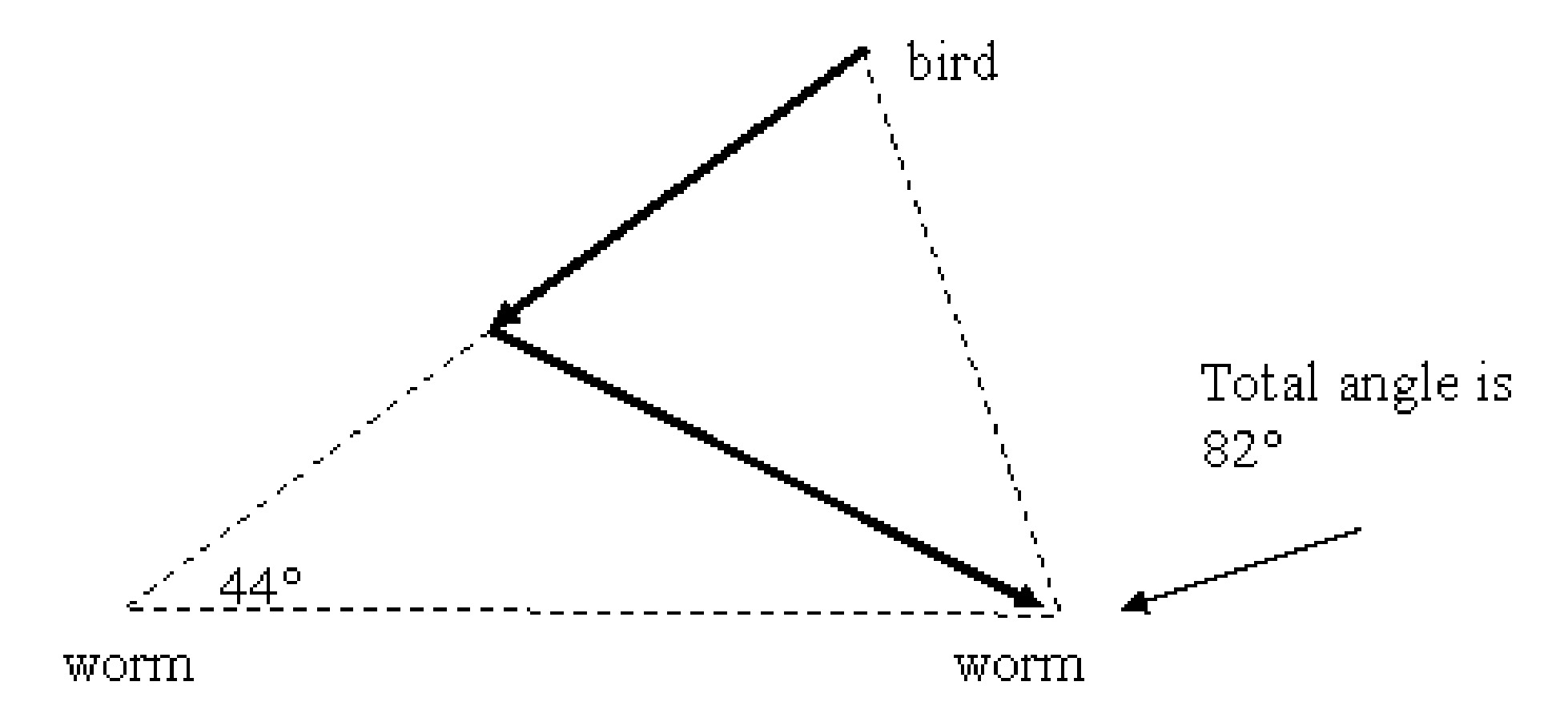
A bird sees two worms on the ground. The worms are 23 inches apart. The bird flies at the worm on the left, but when it’s exactly halfway to the worm, it turns and flies to the worm on the right. The angles are as marked, and the angle marked $82^\circ$ refers to the entire angle on the right side. Find all the other lengths and angles in the diagram below.
Use the law of cosines to determine the angles in a triangle that has sides of lengths 7.3, 23.1, and 15.7. Why would this problem be easier if the sides were 8.1, 23.9, and 16.2?
In the figure below, find AB.
A balloon, B, is tethered to the ground by wires
$\overline {AB} $ and $\overline {CB} $ as shown in the
figure below. How high, $h$, is the balloon above the
ground?

In any triangle $ABC$, prove that $m\angle C = {\cos ^{ - 1}}\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}} \right)$.
Exploring in Depth
Borga and Dhaka City are two of the main cities in
Bangladesh. Borga Airport and Dhaka City Airport are 260 km
apart. The ground controllers at Dhaka City monitor planes
within a 100-km radius of the airport.

Plane 1 is 220 km from Borga Airport at an angle of ${32^ \circ }$ to the straight line between the airports. Is it within the range of Dhaka City Ground Control?
Plane 2 takes off from Borga Airport toward Dhaka City Airport at an angle ${\theta ^{}}$ with the line between the airports. If ${\theta ^{}}$ is small enough, there is a point when Plane 2 first comes within range of Dhaka City Ground Control, and another point when it is last within range. Is there a value of ${\theta ^{}}$ for which Plane 2 is within range of Dhaka City Ground Control at just one point? If so, what is the magnitude of this angle?
If $\theta = {15^ \circ }$, how far will Plane 2 be from Borga Airport when it first comes within range of Dhaka City Ground Control? How far from Borga Airport is it when it is last within range?
A triangle has six parts: three sides and three angles.
If we know only two out of the six parts of a triangle, is it enough information to precisely describe what triangle it is? Explain.
What if we know its three angles? Is it enough information to precisely describe that triangle? Explain.
What is the minimal information about the six parts of a triangle needed to precisely describe a triangle?
Don’t use a calculator for this problem.
Reduce: $\dfrac{{{x^2}y + {y^2}x}}{{xy}}$
Reduce: $\dfrac{{4x - 20y}}{{16x + 20y}}$
Simplify: ${\left ( \dfrac {84x^5y^2} {14x^{-2}y^4} \right )}^{-2}$
Rewrite using fractional exponents: $\sqrt {\sqrt[3]{\sqrt x }} $
If $a = \sqrt b $, find ${a^3}$ in terms of $b$.
As you may have explained in Problem 41, in general a triangle is determined by three of its six parts, where at least one of these parts is a side. These are the possibilities. Case SAA: when one side and two angles are known. Case SSA: when two sides and the angle opposite one of those sides are known. Case SAS: when two sides and the included angle are known. Case SSS: when the three sides are known.
In the Case SSA described above, what can we say about a triangle for which two sides and the angle opposite one of those sides are known?
Note: Case SSA is known as the ambiguous case. Are there good reasons for this name?
Find the side lengths and measures of the angles of $\triangle ABC$ if $m\angle A = {43.1^ \circ }$, $a = 186.2$, and $b = 248.6$.
Find the side lengths and measures of the angles of the angles of $\Delta {ABC}$ if $m\angle A = 42^\circ$, $a = 70$, and $b = 122$.
The Ambiguous Case
In Case SSA, when two sides and an angle opposite one of those sides are given, it is possible that none, one, or two triangles may exist satisfying the given information. These possibilities are illustrated in the figure below, where $\angle A$, $a$, and $b$ are the angle and two sides given. For each case, (a) through (d), explain how $\angle A$, $a$, and $b$ are related.

In the figure below, find X.

In the figure below, find the lengths of the other two sides of this quadrilateral.
Heron’s Formula
Suppose you have $\Delta {ABC}$.
Prove that its area, A, is given by $A = \frac{1}{2}ab\sin C$
Prove that${A^2} = \frac{1}{4}{a^2}{b^2}\left( {1 - \cos C} \right)\left( {1 + \cos C} \right)$
Use the Law of Cosines to express $\cos C$ in terms of $a$, $b$, and $c$, and from Part b prove Heron’s Formula: $A = \sqrt {s(s-a)(s-b)(s-c)}$,
where $s = \frac{1}{2}\left( {a + b + c} \right)$ is the semiperimeter of the triangle.