Introduction
Picture your favorite seat on a gently turning Ferris wheel, the hub of the wheel of a bicycle ridden along an undulating country road, that chip on the rim of the wheel of the old trolley as it hits the smooth flat road, or the middle rung of a ladder as the ladder slides down a wall and along the flat ground.






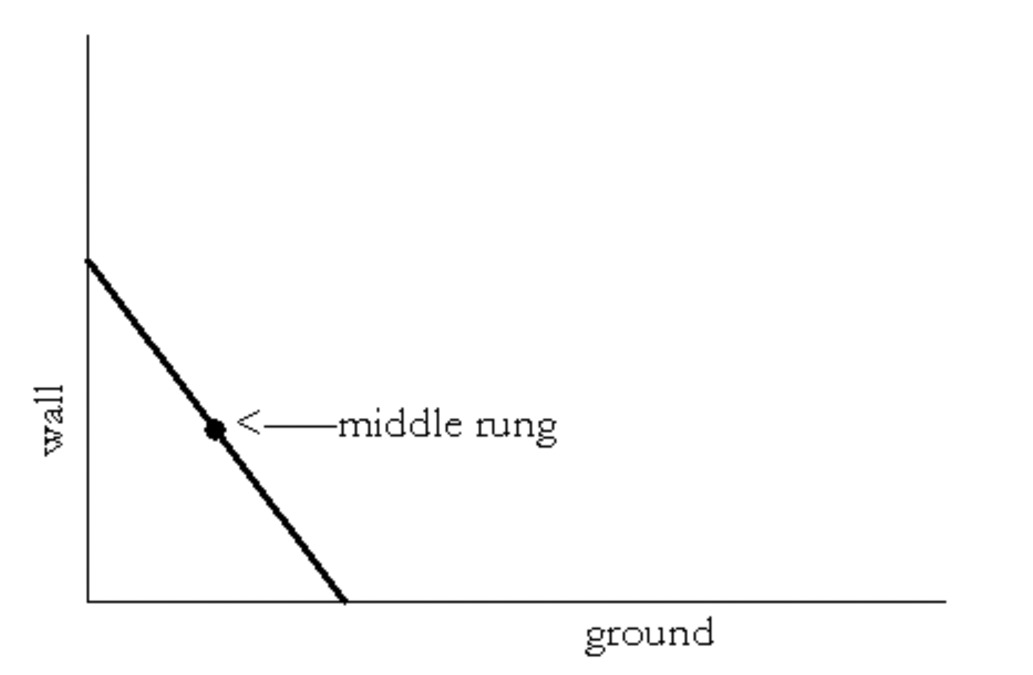
Sketch the path of:
The Ferris wheel seat.
The wheel’s hub.
The chip on the rim of the wheel of the old trolley. (Experiment with this one a bit.)
The ladder’s middle rung. (Experiment with this one a lot.)
To check your answer to problem 1d, try the webpage, http://homepage.mac.com/dscher/ladder.html
These four familiar settings provide a peep into a very interesting concept in mathematics. In the first instance, you might have drawn a circle for the path of your favorite seat. Mathematicians would refer to this path as the locus (plural, loci) of the seat, and would perhaps state it more formally/awkwardly as follows:
“The locus of the seat of the Ferris wheel is a circle whose center is the axis of the Ferris wheel and whose radius is equal to the distance from your seat to the axis.”
So, in general, the locus of an object or point is the graph of all the possible positions the object or point could occupy under certain restrictions. This is the focus of our lesson. We will try to describe loci in words as well as in equations where possible, as well as to recognize shapes represented by particular equations.
[For this lesson you will need to have a protractor, ruler and compass.]
Development
For each of problems 2 through 7 do the following: On a sheet of graph paper set up coordinate axes. Find a point which satisfies the stated condition, and label it $P$. Draw as many such points $P$ as you can. Decide whether these points form any particular shape. If so, describe that shape.
The $x$-coordinate of the point is 5.
The point is always equidistant from the two points $A\left( {3, - 5} \right)$ and $B\left( { - 1, - 3} \right)$.
The $x$-coordinate of the point is always less than or equal to the $y$-coordinate of the point.
The distance of the point from the $x$-axis is always twice its distance from the $y$-axis.
The distance from the point to the origin is always 6.
First graph the points $M\left( {2,3} \right)$, $A\left( {6,3} \right)$ and $C\left( {2,7} \right)$. Now the restriction on a point $P$ is that the points $P$, $M$, $A$ and $C$ must form a parallelogram. What is the locus of $P$?
Remember, when you describe something, be sure that your description is complete. It should thoroughly cover every aspect of what’s being described.
Your description should also be unambiguous. This means that it should be completely clear, and not open to any different interpretations. You should ask yourself, “Would it be possible for the reader to read my description carefully, but misunderstand what I mean?” If so, you know you need to be more specific.
Finally, your description should be understandable to the intended reader.
One could describe the locus of $P$ in problem 3 as the perpendicular bisector of the line segment $AB$. Describing a locus in words makes it relatively easy to draw the locus, but it is also useful to describe the locus with an equation or equations, when this is possible. An equation allows you to find specific locus points quite quickly.
Returning to problem 3, in which $P$ is always equidistant from the two points $A\left( {3, - 5} \right)$ and $B\left( { - 1, - 3} \right)$, let the coordinates of $P$ be $\left( {x,y} \right)$.
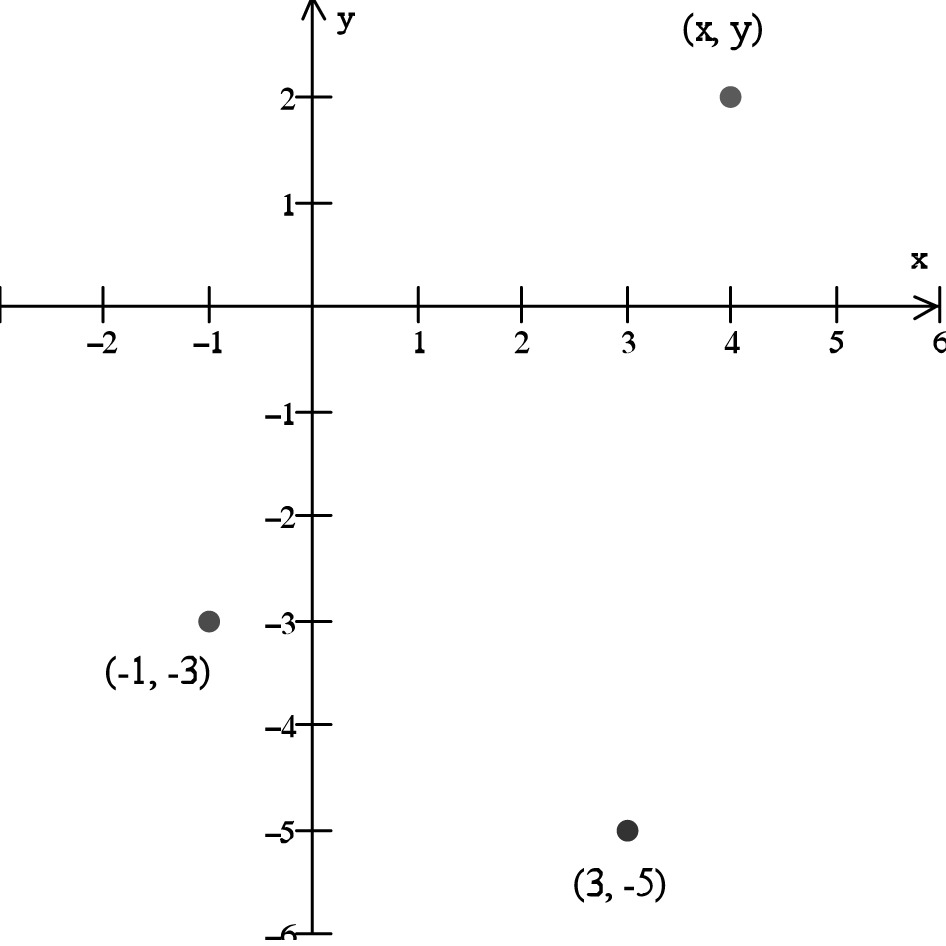
The condition for $P$ could be written “The distance from $P$ to $A$ is the same as the distance from $P$ to $B$.” Using the coordinates and diagram above, translate this sentence into symbols.
In part a, you should have written an equation. Simplify this equation as much as possible.
Check your answer in part b for plausibility in a couple of ways.
First check to see that the point $(1, - 4)$ satisfies your equation in part b. Why must this be the case?
Second, choose any other point whose coordinates satisfy your equation and do a calculation to see if the distance from that point to $A$ and $B$ is the same.
Returning again to problem 3, let’s check to see if your description of the locus was indeed correct.
Find the slope and midpoint of $\overline {AB} $.
Use your answers for part a to find the equation of the perpendicular bisector of $\overline {AB} $.
Looking again at problem 6, with the help of distance formula or Pythagoras’ Theorem, write an equation to describe the path of the point $P$.
Write an equation/inequality for the locus in each of the following. Also, in each case check that your answer is plausible by seeing if a couple of easily tested points indeed satisfy your equation.
Problem 2 ($P$’s $x$-coordinate is 5.)
Problem 4 (The $x$-coordinate of $P$ is always less than or equal to the $y$-coordinate of $P$.)
Problem 5 ($P$’s distance from the $x$-axis is always twice its distance from the $y$-axis.)
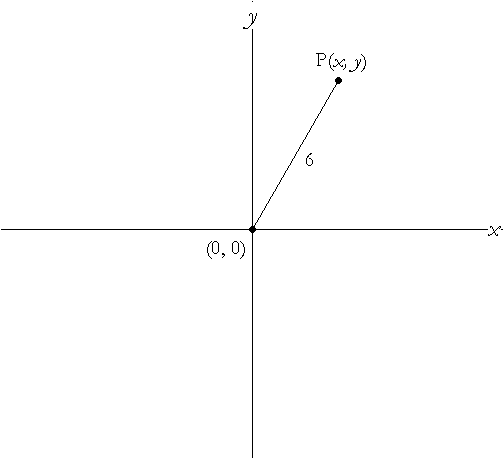
The distance from $P$ to the point is always 6.
Describe the locus of $P$.
Write an equation for the locus of $P$.
The distance from $P$ to the point $S\left( {h,k} \right)$ is always $r$.
Describe the locus of $P$.
Write an equation for the locus of $P$.
Check that your answer for part b is reasonable when h and k are negative numbers far from zero and $r$ is a small positive number, and then check it again for when $h$ and $k$ are negative numbers close to zero and $r$ is a large positive number.
Describe the locus of the point whose equation is:
${(x - h)^2} + {(y - k)^2} = {r^2}$
${(x + 4)^2} + {(y + 13)^2} = 100$
The equation of the locus of point $P$ is given. Describe or draw the graph of the locus. (Making a chart first could be quite useful.)
$x + y = 10$
$x = \left| y \right|$
${x^2} = {y^2}$
One could argue that in some cases a description of a locus by equation is better than a description in words. What do you think? Give a couple of examples to support your position.
Practice
In each case describe the graph and, if possible, write an equation for the locus of $P$. Make sure to check that the equations you come up with are plausible, by checking a couple of interesting and/or “extreme” points that “should” be part of the locus.
The $x$-coordinate of $P$ is always 7.
$P$’s distance from the $y$-axis is three times its distance from the $x$-axis.
$P$’s distance from the $y$-axis is always greater than its distance from the $x$-axis.
The distance from $P$ to the origin is always less than 6.
Graph the points $M\left( {5,3} \right)$ and $N\left( {10,3} \right)$. Triangle $MPN$ is always isosceles with base $\overline {MN}$.
Graph the points $E\left( {-5,3} \right)$ and $D\left( { - 10,3} \right)$. Triangle $EPD$ is always equilateral.
Draw or describe the locus of a point $P$ whose coordinates satisfy the equation $3x + 4y = 12$.
Write an equation for the locus of a point which is always 7 units from the point
$\left( {2,-7} \right)$.
$\left( {10,8} \right)$.
Describe the locus of a point whose equation is given by ${(x - 2)^2} + {(y + 4)^2} = 25$.
Problems
Describe the following loci.
$P$ is equidistant from the points $A\left( {3,5} \right)$, $B\left( {3,8} \right)$ and $C\left( {10,8} \right)$.
$P$ is equidistant from the points $A\left( {3,5} \right)$, $B\left( {3,8} \right)$, $C\left( {10,8} \right)$, and $D\left( {11,5} \right)$.
$P$ always forms a triangle with the points $R\left( {3,-5} \right)$ and $S\left( {-1,4} \right)$.
Describe the locus given by each of the following equations:
${x^2} - 4x + 4 + {y^2} + 8y + 16
= 25$
(Hint: recall that ${x^2} - 4x + 4 = {\left( {x - 2}
\right)^2}$ and ${y^2} + 8y + 16 = {\left( {y + 4}
\right)^2}$.)
${x^2} + 6x + 9 + {y^2} - 10y + 25 = 1$
${x^2} + 10x + {y^2} - 6y = 15$
If you wish to plant some trees so that each tree is equidistant from every other tree, how many trees are you able to plant?
Graph the points $J\left( {2,-6} \right)$ and $L\left( {2,10} \right)$. In each case describe the locus of $P$. (You might want to do some careful drawing.)
$P$ is such that $PJ + PL$ is equal to 16 units.
$P$ is such that $PJ + PL$ is equal to 18 units.
Graph the points $A\left( {0,-3} \right)$ and B$\left( {0,7} \right)$. $P$ is always 4 units from the line segment $AB$. Describe the locus of $P$.
What would the locus of the points a distance 6 from $\left( {0,0} \right)$ be if one could only move an integral amount left/right and up/down?
Graph the points $M\left( {2,3} \right)$, $A\left( {5,7} \right)$ and $C\left( {-1,5} \right)$. Point $P$ is such that the points $P$, $M$, $A$ and $C$ always form a parallelogram. Describe the locus of $P$ as fully as possible.
With harder problems that have formulas that you are deriving, a plausibility check is a necessity, as it is all too easy to make a conceptual or algebraic mistake when coming up with the equation, and a plausibility check is a quick way to see if you have made some kind of error. For the next few problems be sure to make a plausibility check so that you can be more confident your answer isn’t flawed.
Graph the points $R\left( {5,0} \right)$ and $S\left( {-5,0} \right)$ . Point $P$ is such that the angle $RPS$ is always a right angle.
Describe the locus of $P$. (Carefully plot points on graph paper, using a protractor or some object with a ${90^o}$ angle.)
Write an equation for the locus of $P$.
What general statement do parts a and b suggest?
Point $P$ is such that its distance from the point $\left( {0,2} \right)$ is the same as its distance from the line$y = - 2$.
Carefully sketch the locus of $P$.
Describe the shape of the locus.
Write and simplify an equation for the locus.
Construct a locus problem different from the ones you have encountered in this lesson.
Exploring in Depth
Graph the points $M\left( {5,3} \right)$ and $N\left( {10,3} \right)$. Triangle $MPN$ is always isosceles. What is the locus of $P$?
Graph the points $R\left( {5,0} \right)$ and . Point P is such that the measure of $\angle RPS$ is always ${30^ \circ }$. The locus of $P$ seems to be two pentagons, one at the top of $\overline {RS} $ and one at the bottom. What do you think? Be sure to make a cogent argument.
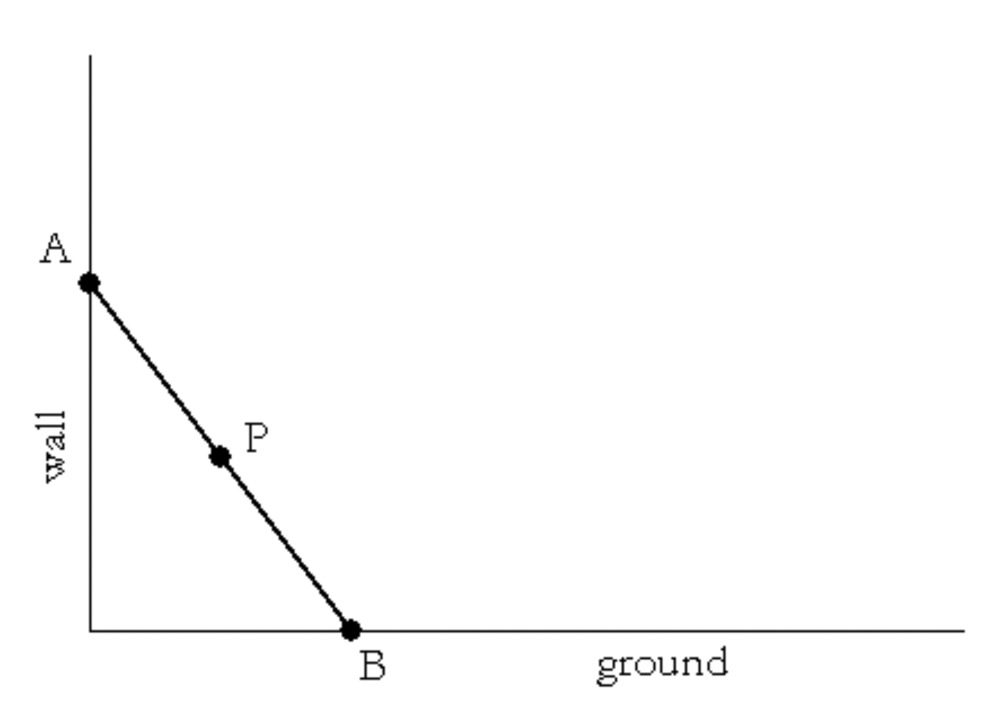
The diagram below models the ladder problem of problem 1. Find the equation of the locus of the midpoint of the ladder $\overline {AB} $ as $A$ slides along the wall and $B$ along the ground. (Hint: besides the length of the ladder another length remains constant throughout the motion.)
$E$ is the point $\left( {3,5} \right)$ and $T$ is the point $\left( {3,11} \right)$. Describe and find an equation for the locus of $P$, given that the area of triangle $EPT$ is always 12 cm$^2$.
In the spiders and flies game, flies fly in circles and spiders crawl on horizontal lines. In this particular game, the flies must fly in circles with center $\left( {0,1} \right)$. And here is the rule for spiders: Spiders crawling on a line $r$ units from the $x$-axis can only catch flies that are moving on the circle whose radius is $r$. So flies will be caught at the points $P$ and $Q$ in the diagram below.
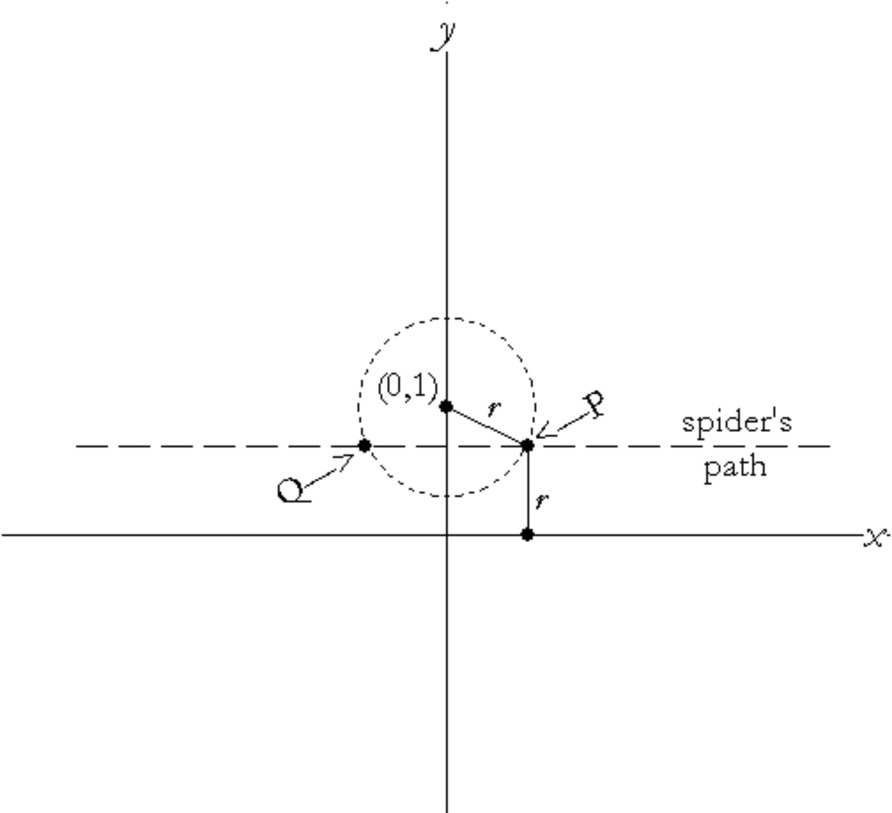
Suppose flies were flying on the circle with radius 5. At what point would they be caught by spiders?
Would any flies be caught at the point $\left( {2,2.5} \right)$ ? How about the points $\left( {1,1} \right)$, $\left( {3,3} \right)$ and $\left( {0,0.5} \right)$?
Carefully sketch the locus of the point where a spider catches a fly.
Describe the shape of the locus.
Write and simplify an equation for the locus.
In one spiders and flies game in problem 35 the equation of the locus of the capture is $y = 4{x^2}$. What are the rules for this particular game?
Don’t use a calculator for this problem.
Reduce: $\frac{{{a^2} - {b^2}}}{{a + b}}$
Separate and reduce: $\frac{{\sqrt x + {x^2}}}{{\sqrt {{x^3}} }}$
Simplify: $\sqrt[3]{x \sqrt{x \sqrt[6]{x}}}$
Simplify: $\frac{4^{-1}+4^0+4^\frac{1}{2}}{4^{-1}-4^{-\frac{1}{2}}}$
If ${2^x} = 7$, what is the value of ${2^{2x + 1}}$?