Introduction
Designers, poets, mathematicians, and most everyone appreciates patterns. Our bodies and minds like patterns, such as sequences of behaviors and mental practices that are organized and efficient, like the pattern of actions you follow in coming to school every morning and the procedure you know to solve a particular class of problems.
You saw patterns of numbers that formed sequences when you worked with arithmetic sequences, such as: 3, 8, 13, 18, …. Below are three sequences. Which two of the three share a common characteristic? What is that special effect?
Putting a picture on a copier and hitting the 100% enlarge button five times; and then creating a sequence of numbers representing the widths of each of the five different images.
Taking a cherry from a bowl, then taking 3 more than the first pick, then taking 6 more than the second pick, then taking 12 more; and then writing down the number of cherries that you have taken one time after the other.
Starting with a cookie, take away half a cookie, then take away a half of the remaining portion, then another half of what remains, and another half; and then creating a sequence of how much of the original cookie remained after each removal.
Development: Geometric Sequences
Earlier you considered arithmetic sequences, which are sequences having a common difference, $d$, between terms. So we would be inclined to describe the sequence 6, 10, 14 as an arithmetic sequence, for we could see the sequence having a first term ${T_1} = 6$ with $d=4$.
The two sequences in problems 1-3 above that were similar are referred to as geometric sequences. How would you describe them in English?
The next term of the sequence 2, 6, 18, 54 could be 162, as the sequence begins with 2 and each succeeding term can be created by multiplying the prior term by 3. So we could say it was a geometric sequence where each term after the first is created by multiplying by 3, so $54 \cdot 3 = 162$. We will call 3 the multiplier, or common ratio.
In the sequence 2, 6, 18, 54, 162, …, we can represent the first term, 2, as ${T_1}$, the second term, 6, as ${T_2}$, etc.
How would you represent the third term, ${T_3}$, in terms of ${T_1}$ and the multiplier?
How would you represent the fourth term, in terms of ${T_1}$?
How about the $n$th term, ${T_n}$?
If we had the geometric sequence 5, 10, 20, what would ${T_5}$ and ${T_7}$ be?
In the last problem if you weren’t told that the sequence was geometric, you could think that the sequence 5, 10, 20, … wasn’t geometric. You might well have noticed that the successive differences between terms form a pattern: first 5, then 10; so this could lead you to think that the next term of the sequence would be 15 more than the prior term of 20; namely, 35. In general any sequence, no matter how many terms are given, is open to the next term being of infinite possibility — if one is clever enough to choose it so that it fits the form of the sequence terms.
If the sequence had 35 after 20, how could you argue that the sequence wasn’t geometric?
Considering the geometric sequence: 4, 6, 9, …,
What would you say would be the next two terms?
How would you write the general term, ${T_n}$, of the sequence?
Can you describe another pattern beginning with the terms 4, 6, and 9 that would not be geometric? What would be the 6th term?
Create values for $a$ and $b$ that establish patterns for each of the following sequences. See if you can generalize by expressing mathematically the general term, ${T_n}$. [Note: these need not be geometric sequences.]
16, $a$, 24, $b$, …
17, $a$, 1, -7, …
4, 2, 8, $a$, $b$, …
1, 2, 4, a, $b$, …
6, 1, $a$, 1/36, $b$, …
The following sequences are to be geometric.
Find $x$: 5, $x$, 125?
What about in the sequence 15, $x$, 375?
How about $\frac{5}{2},x,\frac{{125}}{2}$? And $\frac{2}{5},x,\frac{2}{{125}}$? What is $r$, the multiplier?
Can you create a proportion for each of these three-term sequences so that the common ratio, $r$, can be easily observed?
What would you think the graph of a geometric sequence would look like? Choose some geometric sequence and draw the graph with the number of the term, $n$, on the $x$-axis and the value of the term, ${T_n}$, on the $y$-axis. How would you compare this image to the one obtained by drawing an arithmetic sequence?
Practice
Suppose ${T_n}$ is a geometric sequence with ${T_1} = 2$ and multiplier $r = 1.5$. Find the 4th term and the 14th term. How many terms would you need before the sequence contains the first value beyond 100,000?
For a geometric sequence let ${T_1} = 4$ and let $r = \frac{1}{2}$. What would the 4th term and the 14th term be of the sequence? What would you guess would be the 4th and 14th terms if you halved $r$? Check your guess.
Suppose in a geometric sequence ${T_4} = 1$. Find ${T_1}$ if $r = \frac{1}{4}$.
Create three geometric sequences where ${T_2} = 16$, such that one would increase, one would decrease, and one would oscillate between positive and negative numbers.
Problems
Choose a number between 0 and 1 and let this be the value of $r$ for a geometric sequence. Now, let the first term of this sequence be 2. What will happen to the sequence values as you find more and more terms?
If ${T_1} = 6$ and ${T_6} = 6144$ in a geometric
sequence, find
If ${T_5} = 640$ in a geometric sequence, what value of $r$ would make ${T_8} = 40960$?
In a geometric sequence, if the 2nd term is 85 and the 7th term is -27, then:
Would the 30th term be positive or negative?
What about the 1,259,776,901st term?
Is there a sequence that can be claimed to be both arithmetic and geometric?
Can you create an arithmetic sequence where the terms tend to get closer and closer to 0, without ever going past 0, as you continue to create more and more terms?
How would you describe the impact $r$ has on the value of the terms in a geometric sequence? Be careful in choosing $r$— see what happens if it is positive or negative. Also, are the effects on the geometric sequence different if 0< $r$<1 versus $r$>1?
Write two geometric sequences that begin with the same value, but where in one the tenth term is positive, and in the other the tenth term is negative.
If ${T_n} = 3{\left( {\sqrt 5 } \right)^n}$, what are all the values of $n$ that would make ${T_n}$ rational?
The function $Next(a,b)$ takes any two consecutive terms of a geometric sequence and gives you the next term (assuming $a$ is the earlier term and $b$ is the later term).
What is $Next(14,42)$?
What is $Next(A,1)$?
Write an equation for $Next(a,b)$.
What is $Next(3,Next(3,12))$?
In a geometric sequence $A_{n}$ with common multiplier $r$,
What is the ratio of $A_{8}$ to $A_{5}$?
What is the ratio of $A_{3}$ to $A_{9}$?
Draw a 3-sided figure, 4-sided figure, 5-sided figure, and a 6-sided figure. Now draw all the diagonals you can in each figure. How many do you find for each of the four shapes? Does the number of diagonals suggest an arithmetic, geometric, or some other type of sequence? If you put these values in a table, see if you can guess how many diagonals there would be for a 7-sided figure if the pattern continues. 10-sided? Any idea about the $n$-sided polygon?
Bowser and Lulu are playing chess and eating pizza. Lulu asks Bowser what would be the dimensions of a square board that had half the area of the original $8 \times 8$ board. And the dimensions of another square board that would have half the area of the prior one? And half again? Bowser said, “I don’t know. But to keep things in proportion, we should halve the area of our pizza with the 8” radius every time we halve the area of the board.” As Bowser and Lulu are dogs, what would you determine the four consecutive halvings of the board and the pizza to be?
Going Further: Geometric Series
As you saw with arithmetic sequences, we create an arithmetic series by summing the consecutive terms of such a sequence.
Do you recall for any arithmetic series how to express the sum of the first $n$ terms? If not, make up an arithmetic sequence and see if that triggers any memories.
Because we clearly didn’t want to spend time adding all the terms for an arithmetic series when the number of terms is beyond a few, we made a commitment to find a formula. And to do that we had to look at the series in an imaginative way. Well, that holds also for coming up with a formula for a geometric series.
The clever technique that allows us to generate
the formula for the sum of a geometric series is called
“telescoping”. Let’s try the technique with a concrete
instance. Suppose we are asked to find the sum of the
geometric series:
$S = 1 + 2 + 4 + 8 + \ldots 512$.
Now multiply both sides by 2 (since
Use your understanding of what you did in Problem 30 to calculate the sum of the following geometric series: $S = \frac{3}{1} + \frac{3}{4} + \frac{3}{{16}} + \frac{3}{{64}} + \frac{3}{{256}}$.
Use your understanding of what you did in Problems 30 and 31 to describe how to sum up any geometric series.
Practice
Find the sum of the first 11 terms of the following geometric series:
$2 - 10 + 50 - 250 + \ldots $
$6 + 1\frac{1}{2} + \frac{3}{8} + \frac{3}{{32}} + \ldots $
$28 - 14 + 7 - \ldots $
Find the sum, $S$, of the following geometric series:
$8 + 12 + \ldots + 91.125$
$32 + 48 + \ldots + 162$
$1000 + 10 + \ldots + {10^{ - 17}}$
Suppose you had an $8 \times 8$ checkerboard in front of you. Now imagine putting one grain of rice on the first square, 2 grains on the second square, 4 on the third, and continue doubling. (Ask your teacher or a website about the famous story that lies behind this problem.)
Give your best estimate (no calculators or paper, please!) of how many grains of rice there would be on the 20th and 64th squares.
Now calculate how many grains of rice there would be on the 20th square.
What would be the total of all the rice grains up to the 20th square?
What would be the power of 10 that would be closest to the sum of the rice grains on all 64 squares?
Problems
Write the sum of the following series in as compact a form as possible: $375{(1.21)^0} + 375{(1.21)^1} + 375{(1.21)^2} + \ldots 375{(1.21)^n}$
Write the sum of $T_{1}{(r)^0} + T_{1}{(r)^1} + T_{1}{(r)^2} + \ldots T_{1}{(r)^n}$ in as compact a form as possible.
What is the sum of the first 23 terms of the geometric sequence that begins with ${T_1} = 32$ and has $r$= 1.1?
What would be the first term of a geometric
series if the sum of the first 11 terms is 3069 and the
common ratio is
If the first term of a geometric series is ${T_1} = 2$ and $r$= 3, is it possible that the series sum is 4920? Explain.
Look at the formula for the sum of a geometric series, from problem 37.
What do you imagine would happen to the formula if $r$ was between 0 and 1, and the number of terms would be infinite — that is, the multiplication would continue indefinitely?
Using what you just found, what would be the sum of the infinite series $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \ldots $?
What would be the sum of the infinite series $\frac{1}{2} - \frac{1}{4} + \frac{1}{8} - \frac{1}{{16}} \ldots $?
Make up your own infinite geometric series and find the sum. Now see what your classmates came up with.
Don’t use a calculator for this problem.
Add $3^{-1} + 2^{-2}$.
Solve for $x$: ${x^2} + 4x + 1 = 2$.
Simplify $\sqrt {3000000} $.
Simplify $\frac{{{x^3}{y^8} + {x^2}{y^4}}}{{{x^5}{y^7}}}$.
Simplify ${( - 1)^2} + {( - 1)^3} - {( - 1)^4} - {( - 1)^5}$.
Consider an equilateral triangle with sides of length 1. This triangle is considered to be stage number 0 of the Sierpinski triangle. Then the central triangle obtained by joining the midpoints of each side is removed. This is considered to be stage number 1 of the Sierpinski triangle. Stage number 2 is obtained when from each of the three remaining triangles the central triangle is removed, as was done on the initial triangle when going from stage number 0 to stage number 1 (see figure below).
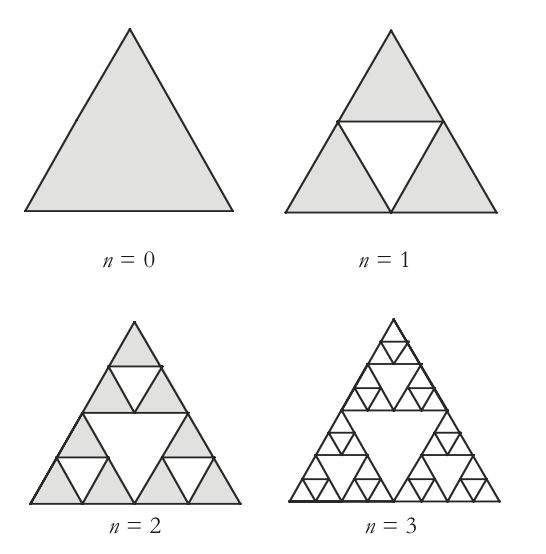
Appropriately shade the last triangle above to examine stage number 3. Then complete the table on the following page.
|
Stage number |
0 |
1 |
2 |
3 |
n |
|
Number of shaded triangles |
|||||
|
Total perimeter of shaded triangles |
|||||
|
Total area of shaded triangles |
Suppose you had the choice of getting paid \$10,000 for your month’s work or getting the amount determined by summing the amount of money you would receive for 30 days, starting with one penny on the first day, and doubling the amount for each succeeding day. Which salary structure would generate the most money? By how much?
Suppose you invested \$50 in an ecology stock, which was doing really well — going up by 1% per month. How much money would your initial investment be worth after a year and a half?
Imagine dropping a ball from a height of 5 feet. Suppose the material it’s made out of and the surface it’s hitting combine to have the effect of the ball bouncing back up two-thirds of the way.
Considering just the falling distances, what would be the total distance the ball fell after 4 bounces? 8 bounces?
Now what would be the total distance for each of these numbers of bounces if you considered its full path — going up as well as down?
What do you think would be the total distance the ball would travel?
Exploring in Depth
Find the sum of the series: $0.7 + 0.07 + 0.007 + 0.0007$. Can you convert this series to have a geometric form? What does your form say the next term would be? Is it correct decimal-wise?
When Jane met Tarzan, Tarzan naturally wanted to show off to Jane and also arrange to get a pair of decent sneakers because his feet were killing him after running on the ground barefoot all these years. To show off a bit, get the sneakers, and save wear and tear on his feet, Tarzan told Jane that he would swing from vine to vine without coming down for an hour. She agreed to give him money for each vine switch, starting with \$1, and then doubling the amount for each subsequent switch (since the same activity gets harder as even Tarzan gets tired over time).
How many vines would Tarzan have to switch in order to get \$60 to buy a pair of sneakers?
If each switch took 5 seconds, how long will he have to stay in the air in order to reach his goal of a pair of sneakers?
A geometric sequence has 4 for the first term, and the sum of the first three terms of the series equals 172. Find the possible values for the common ratio.
How many terms must be added in the geometric series $10 + 5 + 2.5 + \ldots $ in order to first pass the sum of 18? 19? 20?
Here’s a very special sequence from history. It’s called the Fibonacci sequence named after Leonardo of Pisa, whose surname was Fibonacci. He put together the following sequence: 1, 1, 2, 3, 5, 8, Perhaps you’ve seen it before.
What do you think the next two terms of the sequence are?
Do you notice anything about the 3rd, 6th, 9th, … terms?
What about the 4th, 8th, 12th? And the 6th, 12th, 18th? Any conjectures come to mind?
Creating sequences can be great fun and sometimes the outcomes can be quite outstanding.
Consider the sequence 1/1, 3/2, 7/5, … where each succeeding term is created by adding the top and bottom of the fraction to create the new denominator, and adding the top and twice the bottom to get the numerator. Try this for a number of terms. And if you can write or find someone who can write a calculator program, see if you can guess where this sequence is going.
Here is another special sequence: 4/1, 8/3, 32/9, … where to get the nth term first determine if $n$, the number of the term, is even or odd. If it’s even, multiply the previous term by $\frac{n}{{n + 1}}$; if it’s odd multiply by $\frac{{n + 1}}{n}$. See if you get an idea where this sequence is going toward. (From Prime Obsession, by John Derbyshire.)