Introduction: From the Discrete to the Continuous
The town of Tinyville has been growing at a steady rate for many years now. Its population at the end of the last three years is indicated in the table below. The population has been growing geometrically.
|
Year |
2004 |
2005 |
2006 |
|
Population |
212960 |
222640 |
232760 |
What will Tinyville’s population be at the end of 2007? at the end of 2008? $n$ years after 2006?
What will Tinyville’s population be 4.3 years after the end of 2006?
Your answer to Problem 1 Part b is based on an assumption — that is, that the formula for describing Tinyville’s population isn’t restricted to inputting whole numbers. In other words, it seems perfectly natural to assume that Tinyville’s population doesn’t wait until the end of the year to grow; population change is happening on a daily basis, if not hourly, every minute, or even every second. Had you been asked in the lesson on geometric sequences to graph the function you wrote in Problem 1 Part a, the graph would have looked like the graph shown on the left.
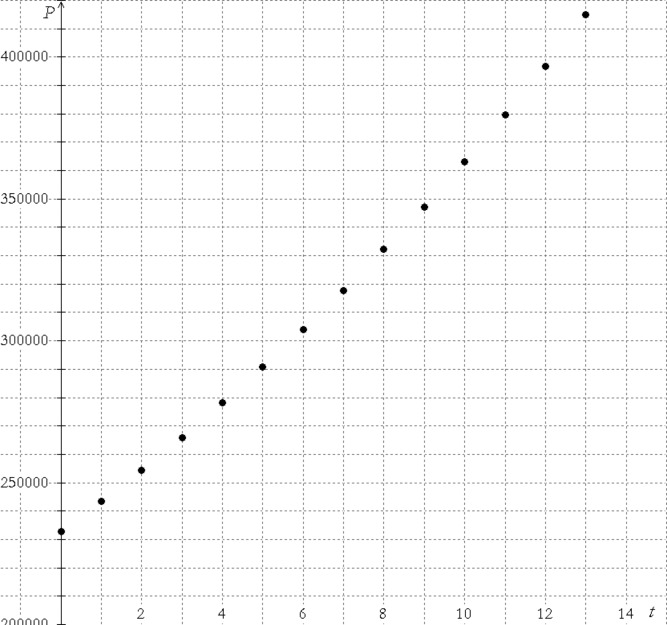
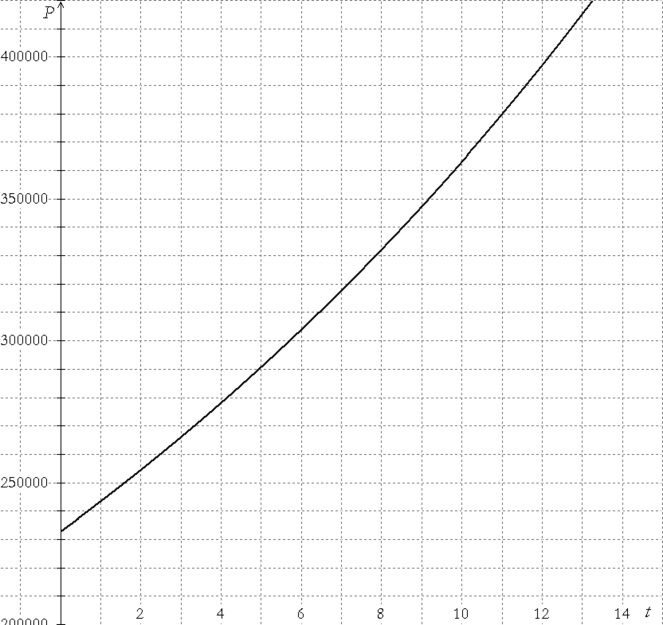
The dots are not connected because $t$ can only take on whole number values. Notice that the ordered pair $\left( {4.3,281839} \right)$ is not a point on this graph. The graph on the right (previous page) was created by assuming that t can take on non-integer values, such as 4.3, 1.67, or 7.3065. It is reasonable to assume that this graph is a more accurate depiction of how Tinyville’s population is growing. Both of the graphs show solutions to an exponential function, but it is the latter graph — the one in Figure 2 — that we will be studying at this point.
Development
To help us transition from the discrete aspect of the geometric sequence graphed in Figure 1 to the continuous aspect of the function graphed in Figure 2, we will introduce some notation. The equation for the first figure could be ${P_n} = 232760{\left( {1.0455} \right)^n}$, where $n \ge 0$. Unfortunately, this kind of subscripting doesn’t allow for ${P_{4.3}}$: there is no such thing as the 4.3rd term of the sequence. We can get around this difficulty by replacing the ${P_n}$ with $P\left( n \right)$ and writing the equation as $P\left( n \right) = 232760{\left( {1.0455} \right)^n}$. Just as with Twist($x$,$y$) or Oblongness($a$,$b$), you don’t multiply $P$ by $n$. We read this equation as “$P$ of $n$ equals…” $P\left( 2 \right)$ is the population two years after 2006 (i.e., $232760{\left( {1.0455} \right)^2} \approx 254423$), and $P\left( {4.3} \right)$ is the population 4.3 years after 2006 (i.e., $232760{\left( {1.0455} \right)^{4.3}} \approx 281839$). This notation is called function notation or Euler notation.
Calculate $P\left( {6.3} \right)$ and explain the meaning of this number in the context of the problem.
If $f\left( x \right) = 5{x^2}$ and $g\left( t \right) = 3 \cdot {2^t}$, then calculate each of the following:
$f\left( 2 \right)$
$g\left( 2 \right)$
$f\left( { - 1} \right)$
An exponential function is any function that can be written in the form $f\left( x \right) = a \cdot {b^x}$, where $a > 0,{\rm{ }}b > 0,$ and $b \ne 1$. We will take a look at these restrictions on $a$ and $b$ shortly, but first let’s explore a couple more problems.
Look back at the work you did in Problem 1. When will the population of Tinyville reach 500,000? Use your calculator to help you answer this questions with 3-decimal place accuracy — i.e., correctly rounded to three digits after the decimal point.
By what percentage does Tinyville’s population grow from year to year? This number is often called the annual percentage growth rate. Where does this number show up in your expression describing Tinyville’s population $t$ years after 2006?
Tinyville’s rival town is Punyville. Punyville’s population at the end of 2004 had reached 375,000 but was now starting to decline geometrically. Its population at the end of each of the past three years is shown in the table below.
|
Year |
2004 |
2005 |
2006 |
|
Population |
375000 |
367500 |
360150 |
What will Punyville’s population be at the end of 2007? At the end of 2008? $t$ years after 2006? Write your answer to the last question using function notation.
What is the annual percentage decay rate for the population of Punyville? How does this number show up in your expression for Punyville’s population t years after 2006?
On a coordinate axis system sketch a graph of Tinyville’s population for $t = 0$ years to $t = 15$ years. On the same coordinate axis system sketch a graph of Punyville’s population over the same time period.
When will the population of Punyville reach 300,000? Use 3-decimal place accuracy.
Based on your graph, when will Punyville’s population first drop below Tinyville’s? Now answer the same question but use 3-decimal place accuracy.
Not too far from Tinyville and Punyville is the town of Smallville. Smallville’s population grew rapidly and reached 610,000 by the end of 2006. Unfortunately, this rapid growth has now precipitated a rapid decline in the population due to overcrowding. The rate of decline is 13% per year.
On the axes you drew for Problem 6 Part c, sketch a graph of Smallville’s population over the same time period as you drew for Tinyville and Punyville.
How does the graph of Smallville’s population over time relate to Punyville’s? What is similar about them? How can you account for this similarity?
Suppose Smallville’s population decay rate had been 10% rather than 13%. Without using your calculator, sketch Smallville’s population over time on the same set of axes as in part a. Now check with your calculator.
Jill’s car is 10 years old and given that it has approximately 170,000 miles on it, she’s considering selling it and purchasing a new car. The initial value of the car was $19,500.
Based on Jill’s research she determines that the car’s value has been depreciating at a rate of 25% per year. To the nearest dollar, how much is the car worth now?
A used car dealer offers to purchase the car from Jill for \$550. Assuming that the dealer believes that this is the actual present value of the car, what depreciation rate did the dealer use to arrive at this price? Solve this problem two ways: using a graph and using algebra. Give both answers accurate to two decimal places.
What can you say about the shape of the graph of $f\left( x \right) = a \cdot {b^x}$ if and $0 < b < 1$? As b increases in value from 0 toward 1 how does the graph change?
What can you say about the shape of the graph of $f\left( x \right) = a \cdot {b^x}$ if $a > 0$ and $b > 1$? As b increases in value how does the graph change?
Suppose $b = 1$ in the equation $f\left( x \right) = a \cdot {b^x}$, where $a > 0$. What does the graph of this function look like? In what way(s) is this graph fundamentally different from the graphs you sketched in Problems 6 or 7? Answer the same question for when $b = 0$.
Now suppose $b = - 2$ and $a = 1$, so the equation is $f\left( x \right) = {\left( { - 2} \right)^x}$.
Without using the graphing or table features of your calculator complete the following table. Make sure to enclose -2 in parentheses when doing your calculations.
|
$x$ |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
$f\left( x \right)$ |
Plot the points you found in Part $a$ and connect them with a smooth curve so as to indicate what the graph of $f\left( x \right) = {\left( { - 2} \right)^x}$ might look like.
Describe how the graph in Part b differs from all the other graphs you’ve sketched in this lesson.
Due to at least one of the differences that you addressed in Problem 12 Part c, mathematicians have decided to limit the values of the base of an exponential function to positive real numbers that are not one.
Practice
On a coordinate axis system sketch a rough graph of $y = {2^x}$. Don’t worry about the horizontal scale, but please make sure that the y-intercept is approximately correct. Now on the same axis system, and without the aid of a calculator, sketch graphs of $f\left( x \right) = 3 \cdot {2^x}$, $g(x) = 1.3^x$, $h(x) = 5^x$, $k(x) = 0.9^x$ , and $m\left( x \right) = {0.5^x}$.
Each function given below models some sort of exponential growth or decay situation. For each function identify the percentage growth or decay rate.
$f(x)=2 \cdot 1.13^x$
$f(x) = 1.02^x$
$f(x) = 3 \cdot 0.82^x$
$f(x) = 385 \cdot 1.97^x$
$f(x) = 103 \cdot 2^x$
$f(x) = 3.7^x$
Bacteria are growing at a rate of 43% per hour. If there are 500 bacteria now how many bacteria will there be this time tomorrow?
How long do you think it will take for the bacteria population in Problem 15 to exceed 10 million? After making an educated guesstimate, come up with a more precise answer as well. Give your answer using three- decimal place accuracy.
Suppose you start to slow down your car in such a way that its speed decreases 10% each second. If your initial speed is 65 mph, estimate how long it will take for your speed to drop down below 35 mph. Then calculate the answer more precisely. Give your answer using two-decimal place accuracy.
If you want to drop the speed of your car exponentially from 65 mph to 35 mph over a ten-second period, then by what percentage should the speed decrease each second? Solve this problem by using algebra and use two-decimal place accuracy.
Let $f\left( x \right) = 4x - {x^2}$ and $g\left( x \right) = {3^x}$. Calculate each of the following:
$f(-5)$
$g(2)$
Determine all values of $b$ such that $100 = 24{\left( b \right)^{10}}$ by using graphs. Use two-decimal place accuracy.
Determine all values of $b$ such that $1.65 = 5{\left( b \right)^8}$ by using algebra. Use three-decimal place accuracy.
Problems
If $f\left( x \right) = 3x + 6$ and $h\left( x \right) = {2^x}$, calculate each of the following. Remember that if parentheses are nested inside of each other, you work on the inside parentheses first.
$f\left( {h\left( 0 \right)} \right)$
$h\left( {f\left( 0 \right)} \right)$
$h\left( {h\left( x \right)} \right)$
$f\left( {{\textstyle{1 \over 3}}x - 2} \right)$
$2h(f(1))$
Determine the values of $a$ and $b$ in $f\left( x \right) = a \cdot {b^x}$ if the following facts are known about $f$.
$\left( {0,3} \right)$ and $\left( {2,5} \right)$ are on the graph of the function.
$\left( {1,2} \right)$ and $\left( {3,10} \right)$ are on the graph of the function.
$\left( {2,3} \right)$ and $\left( {8,1} \right)$ are on the graph of the function.
$\left( { - 3,8} \right)$ and $\left( {1,1} \right)$ are on the graph of the function.
$f\left( 0 \right) = 5$ and $f\left( 3 \right) = 20$.
Isaac Newton determined that the positive difference between an object’s temperature and its surrounding medium decreases exponentially. You place a cup of hot coffee (initial temperature 180° F) on a table in a room (temperature 70° F). The initial difference in temperature is 110°. After 30 minutes the temperature difference is 60°.
Write an equation that models the temperature difference $D$ between the cup of coffee and the room at time $t$. Use function notation with $D$ and $t$.
How long will it take for the temperature difference to drop to 10° F? Use 3-decimal place accuracy.
How long will it take for the coffee to reach a temperature of 75°? Use 3-decimal place accuracy.
(Copyright Phillips Exeter Academy) A helium filled balloon is slowly deflating. During any 24-hour period it loses 10% of the helium it had at the beginning of the 24-hour period. At 10 am on Sunday the balloon initially held 10,000 cc of helium.
How much helium did the balloon contain 3 days later?
Approximately how much time will it take for the balloon to lose half of its initial helium? This time is called the half-life. Use 2-decimal place accuracy.
Approximately how long will it take for the amount of helium in the balloon to drop to 2,500 cc? Use 2-decimal place accuracy.
Approximately how long will it take for the amount of helium in the balloon to drop to 12.5% of its initial amount? Use 2-decimal place accuracy.
In Problems 26-31, you will need to pay close attention to what information you’re being given and what question you’re trying to solve. With exponential growth and decay problems, the fact that something is decaying by 3% monthly doesn’t mean that the base of the exponential function is $3$, $.03$, or even $-.03$. Often, the natural way of expressing a problem doesn’t translate directly into symbolic expressions, so read each problem carefully, pondering the meaning of each term and number that is presented, before venturing into answering the question posed. In doing this, you will be using the habit of re-examine the problem.
An atom of carbon-14 is unstable, meaning that at any moment there is a chance that it will spontaneously change (actually decay) into nitrogen. The half-life of carbon-14 is approximately 5728 years. What is the annual percentage decay rate of carbon-14? Use algebra to solve this problem.
The half-life of californium is approximately 898 years. How long does it take for a given mass of californium to decrease by 99%?
$N$ grams of a substance has decreased to $.2N$ grams after 60 days. What is the percentage daily decrease of the mass of this substance? Use algebra to solve this problem.
Rachel has money in an account that pays her 4% annual interest, compounded yearly.
How many years will it take for the money in her account to double?
How many years ago was it that the amount of money she had in her account was half of what it is now?
You open your locker and discover mold on your favorite snack bread that you inadvertently left in your locker several months ago. The function $M\left( t \right) = 25672486{\left( {1.18} \right)^t}$ describes the number of mold spores found growing on the piece of bread t days after the mold is discovered.
How many mold spores were on the bread 5 days ago?
What is the daily growth rate of the spore population?
What is the hourly growth rate of the spore population? Use change or simplify the problem by thinking about which number in the equation can be changed (made easier) without changing what’s really happening with the mold spores.
Write a function modeling the number of spores on the bread $t$ hours after the mold was discovered.
(Copyright Phillips Exeter Academy) Jennings Bryan Osborne of Little Rock, Arkansas is known for building extravagant displays of Christmas lights. In 1992, Osborne used 1,600,000 light bulbs, which were guaranteed to be of high quality. The probability that any one bulb would burn out in a given 24-hour period was only 0.01 percent. Assuming that Osborne leaves his display on continuously, how many bulbs can be expected to still be working after
1 day?
2 days?
30 days?
Explain why a monthly growth rate of 1% is not equivalent to a yearly growth rate of 12%.
On the axis system shown below are four graphs (A-D) of exponential functions. Propose four possible equations for the graphs and explain how you arrived at your choices.
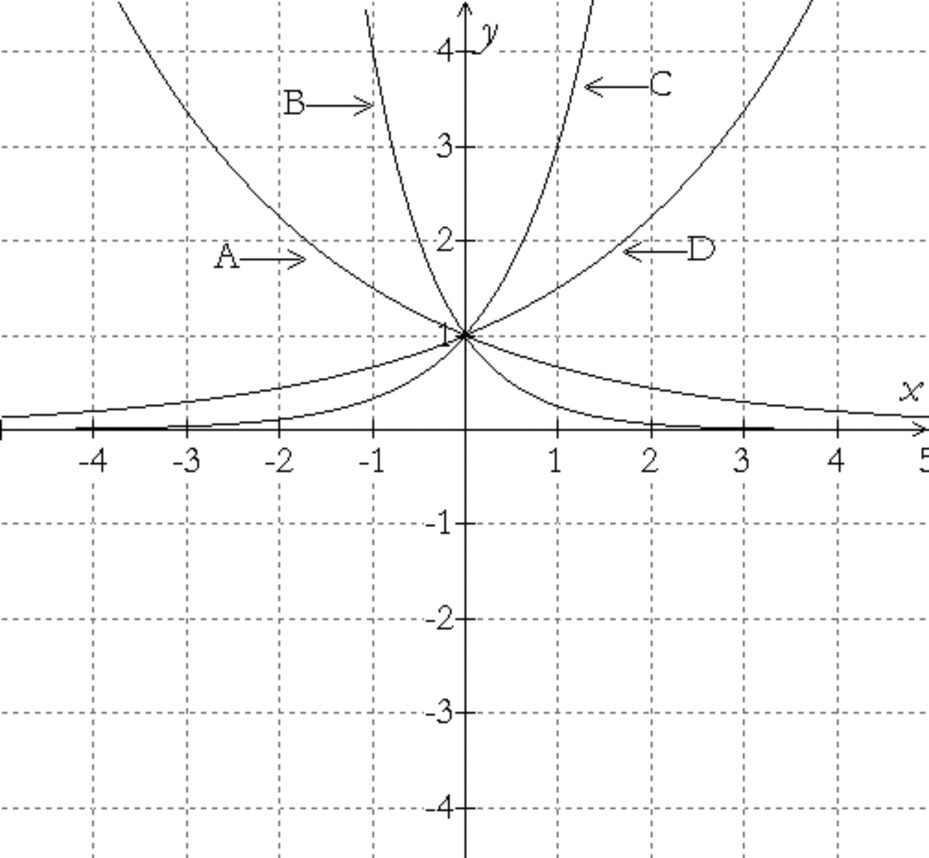
Exploring in Depth
Define $f^{(n)}(x)$ to be shorthand
for calculating $f(f(f(\ldots f(x))))$,
where there are $n$ number of $f$ ’s.
For example, $f^{(3)}(x) = f(f(f(x)))$.
Let $f(x) = \frac{1-x}{1+x}$. Calculate $f^{(2)}(\frac{3}{5}$)
and
How should we interpret expressions like ${4^{3.5}}$? Let’s take a closer look.
Is ${4^6}$ halfway between ${4^5}$ and ${4^7}$? Why or why not?
Is ${4^{3.5}}$ halfway between ${4^3}$ and ${4^4}$?
Rewrite ${4^{3.5}}$ as ${4^{fraction}}$.
Confirm that your answer to part c can be computed without ever using a calculator. Is ${4^{3.5}}$ closer to ${4^3}$ or ${4^4}$?
Use your answer to part a to help answer why your answer to part d makes intuitive sense.
There is another kind of mathematical notation that is similar to function notation. This notation, called mapping notation, looks like the following:
$f:x \to {x^2} - x$.
This notation is read as “$f$ maps $x$ to ${x^2} - x$.” Given this definition of $f$ then, $f:6 \to 30$.
Determine what number goes to the right of the arrow.
- $f: - 5 \to \_\_\_\_$
- $f: (f:5 \to \_\_\_\_) \to \_\_\_\_$
Who came up with this notation? What was the original use for it? Is it still used and in what contexts?
A bank offers 6% annual interest on a savings account, but compounded quarterly. What this means is that the bank will calculate the interest on the account each quarter (4 times per year) but will do this by using a 1.5% interest rate for each of these calculations (1/4th of the annual interest rate). Suppose you invest \$1000 into this account.
How much money will you have in your account at the end of the year?
If the bank changed to giving you interest on a monthly basis, rather than a quarterly basis, how much money would you have in your account at the end of the first year?
Complete the table below.
|
Compounding |
Quarterly |
Monthly |
Daily |
Hourly |
Every minute |
|
Total $ after one year |
1061.36 |
Given how our monetary system works, at what point, if any, do you not gain anymore money as the number of times compounding increases? Would you give the same answer if instead of investing \$1000 you invested \$1 million? Explain.
Don’t use a calculator for this problem.
Name an angle that has a sine of 1. Then name an angle that has a cosine of -1. How many answers are there to these two questions?
Simplify $\frac{{3(x - 4) + 6}}{3}$.
Simplify ${a^2}b\sqrt {{a^5}{b^8}{c^2}} $.
Find the vertex of the parabola with equation $y= -x^2 + 6x - 5$.
Simplify $1 + \frac{1}{1 + \frac{1}{1}}$ .