A person with diabetes takes a shot of 10 units of insulin. The amount of insulin in the bloodstream decays exponentially. 10 minutes later, there are 5.99 units of insulin left in the bloodstream.

Find a formula for the number of units of insulin left after $t$ minutes.

How much insulin is left in the bloodstream after 20 minutes?

How many minutes did it take for the insulin level to get down to 8 units?

A house bought five years ago for $\$100,000$ was just sold for $\$135,000$. To the nearest tenth of a percent, what was the annual growth rate?

A bank advertises that if you open a savings account, you can double your money in 12 years. If you invest $\$100$ in the account, find a formula for the money you’ll have after $t$ years.

An amount $A_0$ of radioactive iodine has a half-life of 8.1 days. In terms of $A_0$, how much is present after 5 days?

What’s the percentage growth rate for this set of data? Then find an equation to describe the data.

$x$	$1$	$2$	$3$	$4$	$5$	$6$
$y$	$20$	$21.42$	$22.94$	$24.57$	$26.31$	$28.18$

Monica begins a chain letter by writing to five friends. In her letter, she instructs them to send copies of the letter to five people apiece. Since the copies of the letter contain the same instructions, the recipients of the copies of the letter will also send copies to five people apiece,
and so on.

Find a formula for the number of people who will receive letters at
the “$n$th” stage of this process. (Consider it to be stage one when Monica is writing her letters. It’s stage two when her friends receive these letters and then write their own, etc.)

How many people will have
received letters all the way through and including stage 10?

Suppose a doctor earns $40,000 during the first year of practice. Suppose also that each succeeding year the salary increases 10%.

How long would the doctor have to work to have a salary of a million dollars?

What is the total of the doctor’s salaries over the first 10 years?

How many years must the doctor work if the sum of all his salaries is to exceed a million dollars?

In a Geometric sequence, $T_3=36$ and $T_7=182.25$.

What is the common ratio?

What is the 10th term of the
sequence?

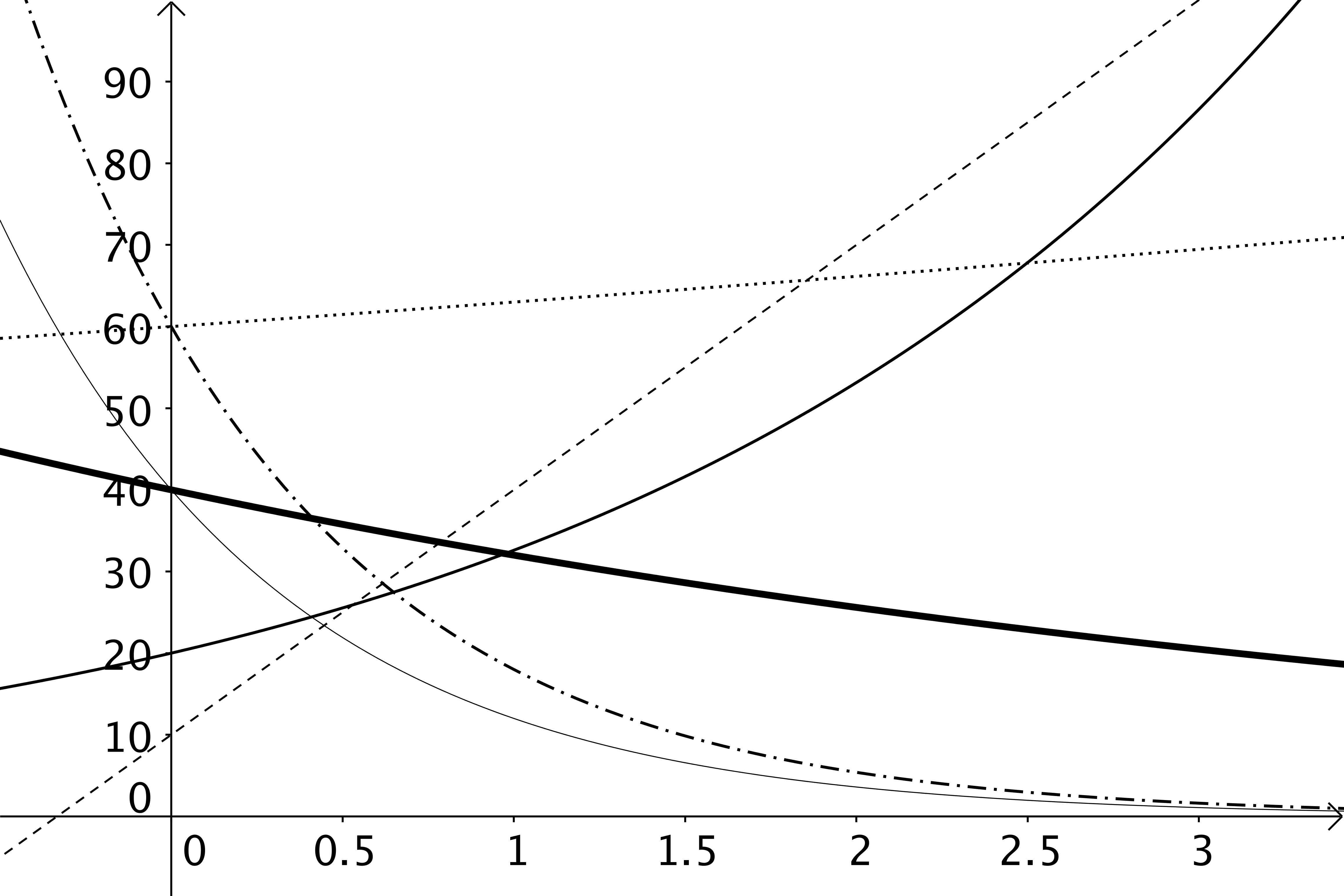
Match the equation to the graph.
$f(x)=20 \cdot 1.63^x$
$g(x)=40 \cdot 0.3^x$
$h(x)=60 \cdot 0.3^x$
$i(x)=30x + 10$
$j(x)=60 \cdot 1.05^x$
$k(x)=40 \cdot 0.8^x$

Let $f(x)=3x-2$ and $g(x) = 2x^2$.
Calculate

$f(g(2))$

$g(f(2))$

$f(f(2))$

$f(1)$

$f(f(f(f(f(1)))))$

You’re solving a modeling problem in
which a millionaire leaves $\$1,000,000$ in
an interest-bearing account and wants
to know how long it will take before
the account holds $\$1,100,000$. Suggest a
reasonable calculator window. (Give the
$x$min and $x$max and the $y$min and $y$max.)