Introduction
An explorer is lost in the 30 by 60 mile rectangular section of snowy wilderness shown below. The search and rescue team knows that she started her journey at the southwest corner, and since there hasn’t been any new snow for a while, they also know that they’ll be able to see her tracks.
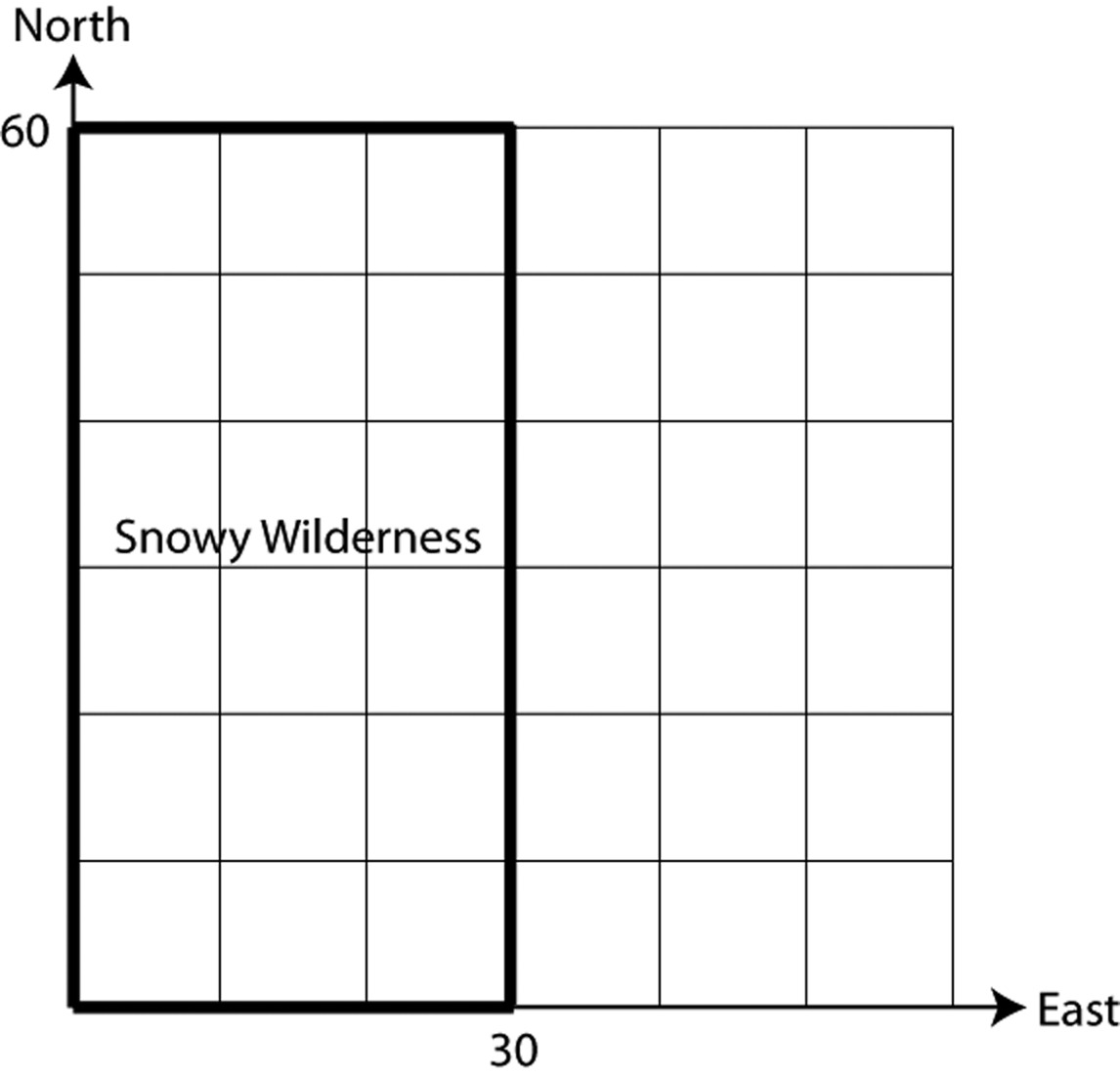
Obviously, the team wants to find the lost explorer as quickly as possible. There are different ideas about how to do this, though, so they decide to split into two groups. Group A will start at the southwest corner and simply follow the explorer’s trail. Group B, though, has a different strategy. Here’s what they do:
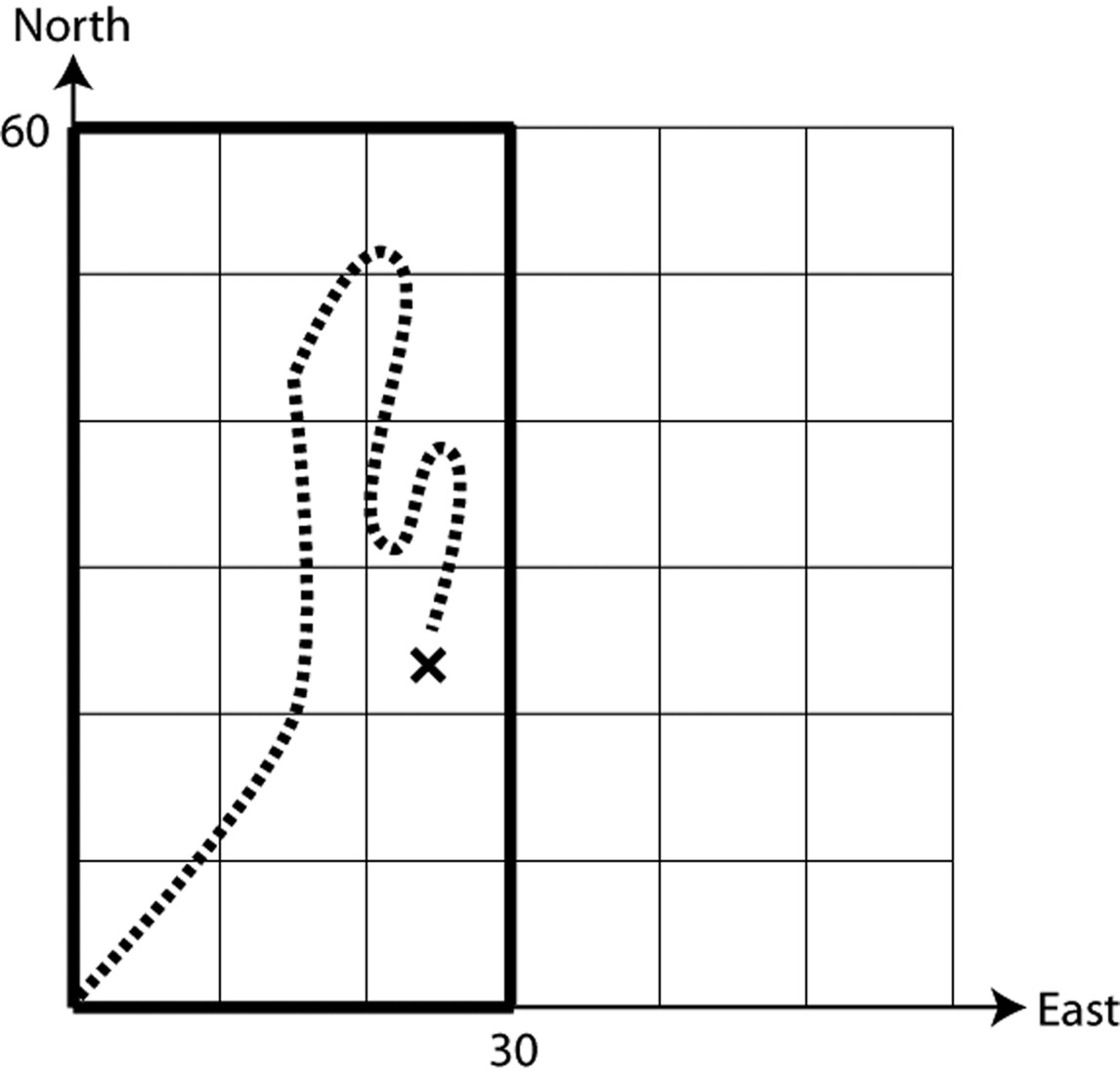
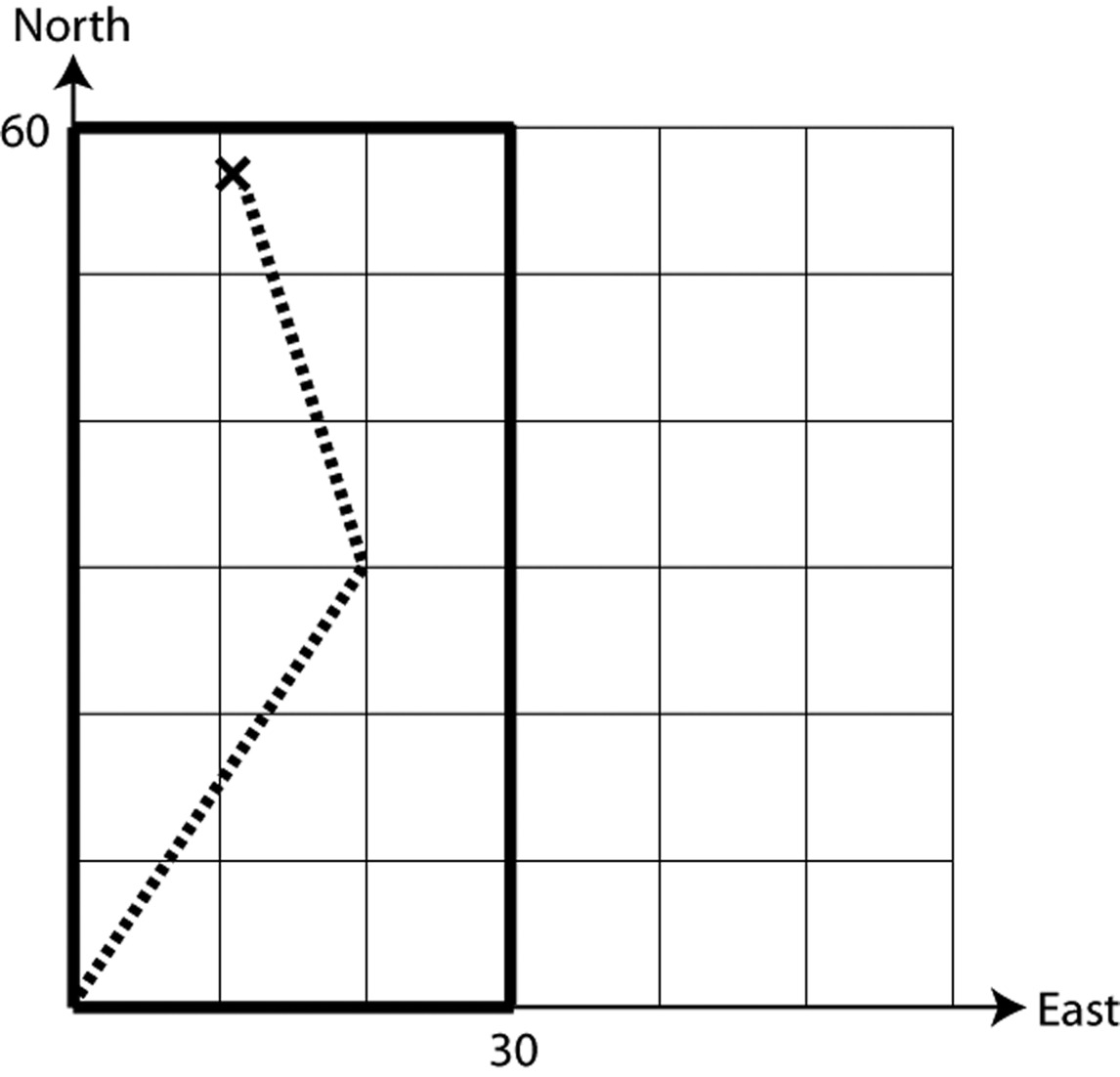
Group B starts out at $\left( {0,30} \right)$, and walks directly east. Every time they cross the explorer’s trail, they make a note of it. Suppose that by the time they reach the eastern border, they’ve crossed the explorer’s trail 5 times. What can they conclude about where the explorer must be now? How about if they’d crossed the trail 8 times?
As you can see, Group B’s west-to-east walk allows them to cut the remaining search area in half. Their idea is to keep repeating this until they’ve narrowed down the search area to a small horizontal strip. Suppose that on the first walk (along $y = 30$), they crossed the trail 3 times.
What horizontal line should they walk next?
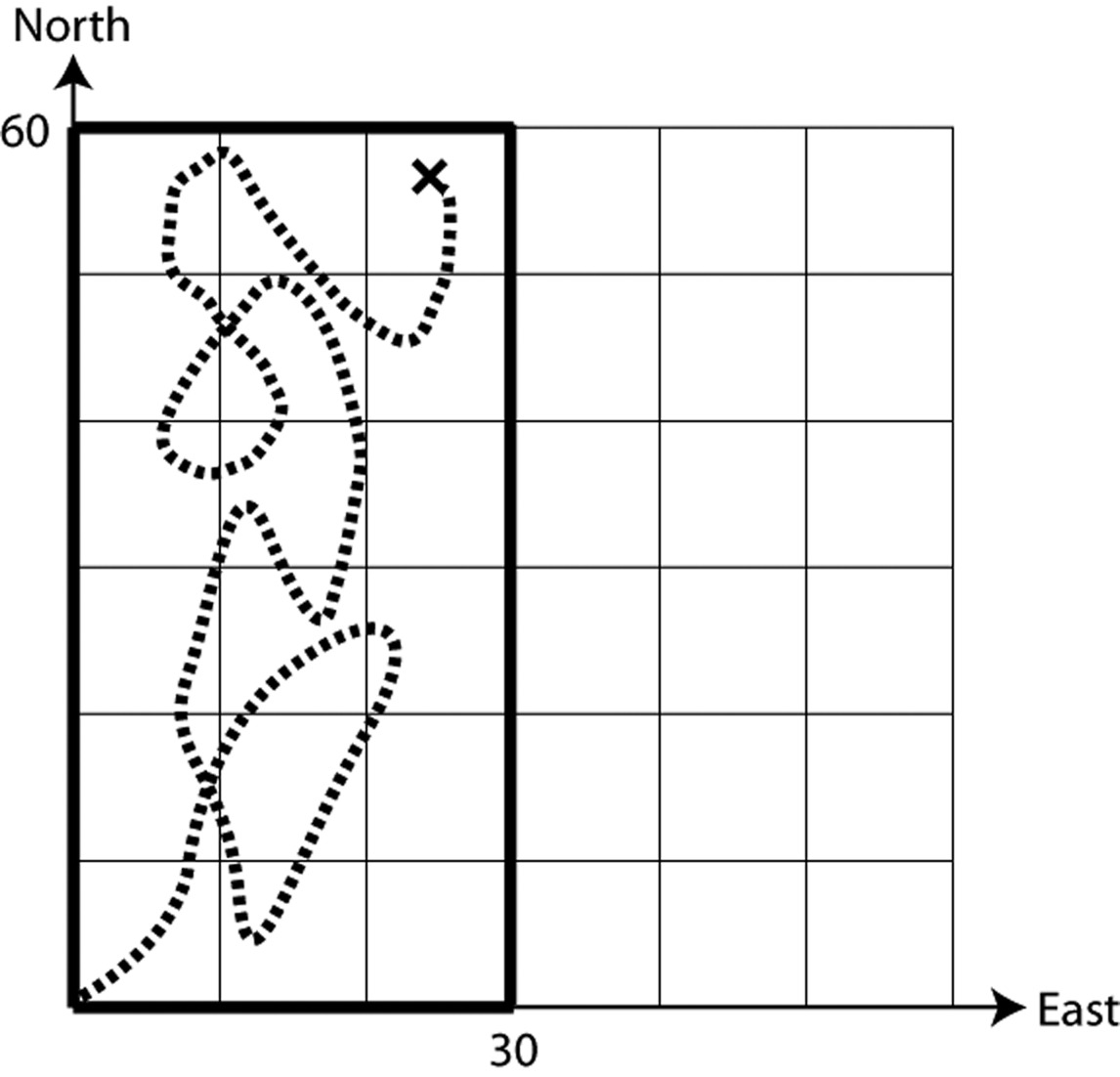
Now, suppose that on the second walk, they cross the explorer’s trail 6 times. Where could the explorer possibly be? Demonstrate your answer by drawing a picture of one such trail the explorer could have taken.
Is Group B’s strategy better than Group A’s? To help you answer this question, determine approximately how long each one would take to find the lost explorer in each of the following scenarios. (Assume that each group moves at the same speed, and that as soon as a group comes within a mile or so, they’ll see the explorer’s signal flares.)
Development
The two strategies in the situation above are both examples of algorithms— though, of course, Group A’s is a rather simple one. An algorithm is simply a clearly defined, step-by-step process for accomplishing a desired task. You can think of every algorithm as having three main parts: input, process and output. In the search and rescue situation, for example, the input would be the whole search area and the explorer’s trail, and the output would be the explorer’s location.
As you can hopefully see, thinking about and analyzing algorithms can be useful in situations where there are multiple possible approaches, and we want the “best” or most efficient one. But this kind of thinking isn’t only useful in practical applications — it’s also a source of some classic games and puzzles.
The Number Devil is thinking of an integer between 1 and 63 (inclusive), and your job is to guess it. If you guess wrong, the Number Devil will tell you (truthfully) whether your guess is too low or too high. Come up with a strategy for finding the Number Devil’s number in as few guesses as possible.
Was there anything in common between your strategy in the previous problem and Group B’s approach to finding the missing explorer? Group B’s strategy — and, likely, yours — is an example of a binary search algorithm. (The Latin root $bini$ means “two-by-two”.) Here’s another application of it.
Your English teacher has an alphabetized stack of 15 papers, but she’s forgotten whose papers she collected. Now, she needs to check and see if she has Gabi’s paper in the stack. She decides to use a binary search algorithm.
Simulate this with your group: have a group member make an alphabetized list of names without showing you. The list maker gets to decide whether or not “Gabi” is in the list. You, in the role of the teacher, can ask for any individual name in the list (e.g., “Who is the fifth person in the list?”). How many times do you have to ask before you can be sure whether or not Gabi’s name is in the stack?
Make up an alphabetized list of 15 names that would force the teacher’s binary search process to make the most guesses possible. This is called a “worst case” input for the algorithm. How many guesses does the algorithm take, in the worst case?
Now, you decide to play a little trick on the teacher. Carefully rearrange the ordering of names you made in part b of the previous problem so that, when your teacher uses binary search, she’ll end up mistakenly concluding that Gabi’s paper is not in the stack.
Based on what happened in problem 6, it’s clear that there are certain situations in which the binary search algorithm isn’t appropriate. This is always true: every algorithm makes some assumptions about its input.
What assumption(s) did the teacher make in using her binary search algorithm?
In addition to thinking carefully about the input, it’s also helpful when working with algorithms to identify the basic operations your algorithm can use. The basic operations are always based on the situation you’re dealing with: they are the actions you’re able to do as a single “step” of your algorithm. In the Number Devil game, for example, your basic operation was to guess a number and find out if it was correct, too big, or too small. In the stack of papers example, the basic operation was to check the name on a single paper in the stack and compare it alphabetically with the name ‘Gabi’. The basic operation in the following game is similar to these two, but slightly different.
Play the following game with a classmate:
Your partner should write five different numbers on slips of paper. Then shuffle the papers and put them face down on the table in a straight row.
You are the guesser. Your job is to figure out which paper has the largest number written on it. But you can never see the numbers themselves — you can only ask for comparisons. For example, you could point to the first slip and the fourth slip, and your classmate would have to tell you which one has the larger number.
Each comparison counts as one step, and your goal is to find the paper with the largest number with as few steps as possible.
Play the game and identify the paper with the largest number. How many steps did it take before you were certain about your answer?
Describe, in detail, an algorithm for finding the largest number in a list of numbers, using as few comparisons as possible.
Aaron has an algorithm that he claims can find the largest number every time using only three comparisons. Either figure out Aaron’s algorithm, or explain why it’s impossible.
Here’s a somewhat different algorithmic puzzle that many consider a “modern classic.” (In fact, the story goes that, before it got out onto the Internet, this was a question that Google interviewers asked of potential employees.)
You have two perfectly identical eggs. You need to figure out how high an egg can fall from a 100-story building before it breaks. You know nothing about the toughness of the eggs; they may be very fragile and break when dropped from the first floor. On the other hand, they may be super tough genetically altered eggs, so tough that that dropping them from the 100th floor doesn’t even cause a scratch. The only thing you know for sure is that they both have exactly the same “toughness.”
Joey takes his first egg, and drops it off of the fourth floor. It doesn’t break. Then, he goes up and drops it off the tenth floor, and it shatters spectacularly on the sidewalk. Finally, he takes his second (and last) egg, and drops it off the seventh floor. It breaks. What can Joey conclude about the toughness of his eggs?
Come up with a strategy for figuring out your eggs’ toughness. Your job is to guarantee the smallest number of egg-drops, in the worst case. You are allowed to break both eggs, but remember, two is all you get!
Practice
You have 16 identical-looking coins. Fifteen of them have exactly the same weight, and one is too heavy. Describe an algorithm for finding the heavy coin in as few steps as possible. The basic operation allowed is to use a simple balance to compare 2 piles of coins to see which pile is heavier.
In the algorithm you use for adding two very large numbers by hand, what are the basic operations? How about multiplying two numbers by hand? Dividing?
Describe the mental algorithm a street vendor might use to quickly make change for a $\$20$ bill. Make sure your algorithm works by testing it out the following sale amounts: $\$1.50$, $\$3.00$, $\$11.45$, $\$17.26$.
Write an algorithm for finding someone’s age based on their birth date and the current date. (For instance, Tom’s birth date is 6/14/90 and today’s date is …. so Tom is …. years old.)
Recall the Number Devil game from problem 4. Now let’s say you’re trying to guess a number between 1 and 255. If you were going to play using the binary search algorithm, what would be one worst-case number that the Number Devil could choose?
Consider the following strategy to the egg-drop problem:
Starting at floor 1, drop the first egg off of odd-numbered floors until it breaks. Then, go back down one floor and drop the second egg. If it breaks, that’s the answer. If not, then the floor above is the answer.
Say you get to decide how tough the eggs are, and you want to force the strategy above to make the largest possible number of drops before it succeeds.
What is the worst-case input for this strategy? i.e., how tough should you make the eggs?
What’s the worst-case number of drops?
Going Further
The algorithms we’ve worked with so far dealt with lists of information, whether they were lists of numbers, names, phone numbers, etc. Now, we’re going to look at algorithms that transform a single item, such as a number, word, etc.
You and your friend are planning to share lockers, so as soon as you get your combinations, you plan to exchange them over the phone. Each combination has three numbers in it – for example, 11 – 2 – 41.
In case someone might be listening, though, you agree ahead of time to use the following algorithm to encrypt each number in the combination:
${\mathop{\rm EncryptNumber}\nolimits} \left( N \right)$:
If $N$ is odd, then output $2 + N$.
Otherwise, output $2 \cdot N$.
Notice that the notation being used here is similar to the “function notation” that you’ve seen in some previous lessons. “EncryptNumber” is the name of the algorithm, and $N$ is a name for the input to the algorithm.
Your combination is 12 – 7 – 11. What should you tell your friend?
Your friend tells you 80 – 28 – 29. What was her combination?
Your brother wants to use the same system with his friend, but he’s confused about how it’s possible to “decrypt” the numbers he receives. Give him detailed instructions for a “DecryptNumber” algorithm that he can use to understand what his friend tells him.
One convenient feature of using function notation is that we can use it to easily write down things about what an algorithm does for specific inputs. For example, we can write ${\rm{EncryptNumber}}\left( 4 \right) = 8$, or ${\rm{DecryptNumber}}\left( 8 \right) = 4$.
What is ${\rm{DecryptNumber}}\left( {13} \right)$? How about ${\rm{DecryptNumber}}\left( {24} \right)$? And ${\rm{DecryptNumber}}\left( {18} \right)$?
Predict what would happen if you applied the EncryptNumber algorithm to each of your three answers in the previous problem. Then try it out to test your prediction.
When you use an algorithm to encode a message so that no strangers can understand it, it’s called an “encryption” algorithm. This is essentially what a computer does when you enter a password or other personal information on a website, so that nobody besides the website owner can see it.
Another kind of encoding is called “compression”. With compression, the idea is to shrink the size of a message down so it’s faster to transport. This is why mp3’s are such a big deal: they allow you to compress very large song files so that they’re small enough to download quickly.
Emmett wants to compress all the old emails he’s saved on his computer. Thinking of the shorthand he sometimes uses for text messages, he decides to go through each message and remove all the vowels and all the spaces. One problem with this approach is that it simply doesn’t shrink the message by all that much. However, there’s a much deeper problem. What is it? Can you suggest an alternative method for compressing Emmett’s emails?
What are some characteristics that would make a good compression algorithm? What characteristics are absolutely necessary?
You saw with the compression and encryption algorithms above that they’re only useful if they also have decompression and decryption algorithms to go with them. These are two examples of a more general type of algorithm called an inverse algorithm. When you have two algorithms, and each one reverses the other, then the two algorithms are called inverses of each other. Using this language, we can say the major flaw in Emmett’s compression algorithm was that it has no inverse algorithm. (Why not?)
You want to share your gym locker with a different friend from the one in problem 18. But she and your other friend don’t get along, so you need a different code for this locker. Here’s the one you use:
${\mathop{\rm GymCode}\nolimits}
\left( N \right)$:
If $N$ is odd, then output $2N$.
Otherwise, if $N$ is a multiple of 4, output $N + 1$.
Otherwise, output $2N + 3$.
Write an inverse for this algorithm called GymDecode.
Now, let’s say you wanted to write down all your passwords so you don’t forget them. Since someone else might see the paper, you decide to encrypt all the passwords so that only you will know what they really are.
You’ve already got two encryption algorithms: EncryptNumber from problem 18 and GymCode from problem 24. So you can just combine the two to create the SuperSecretCode algorithm, as follows:
${\mathop{\rm
SuperSecretCode}\nolimits} \left( N \right)$:
Output ${\mathop{\rm EncryptNumber}\nolimits} \left(
{{\mathop{\rm GymCode}\nolimits} \left( N \right)} \right)$.
Recall that ${\mathop{\rm GymCode}\nolimits} \left( N \right)$ just means “the output of GymCode when you input $N$”. Similarly, “${\mathop{\rm EncryptNumber(GymCode}\nolimits} \left( N \right))$” means, “the output of EncryptNumber when you input ${\mathop{\rm GymCode}\nolimits} \left( N \right)$”.
What is the value of ${\mathop{\rm SuperSecretCode}\nolimits} \left( {14} \right)$? (Hint: first figure out the value of ${\mathop{\rm GymCode}\nolimits} \left( {14} \right)$, and then use substitution.)
Write the inverse algorithm, SuperSecretDecode.
Practice
I have three bags, two with marbles in them (bags A and B) and one without (bag C). First, I take half the marbles in bag A and add them to bag B. Then I recount the marbles in bag B, take out half, and put them in bag C. You know that when I’m done, the contents of the bags are as follows:
Bag A: 10 marbles
Bag B: 20 marbles
Bag C: 20 marbles
Find out how many marbles were in the bags originally.
Write an inverse algorithm to reverse the following process: Take a number and add 4 to it. Then multiply your answer by 3. Finally, subtract 1 from your answer.
Is there an inverse for an algorithm that sorts a list of numbers in ascending order? (“Ascending order” just means from least to greatest.)
An algorithm takes a number, multiplies it by 2, and then adds 5. If the output from the algorithm is $X$, what was its input, in terms of $X$?
Write an inverse algorithm to reverse the following process: Take an integer between 1 and 99. If it’s a 2-digit number, multiply it by 5. If it’s a 1-digit number, multiply it by 10 and then add 1. (Try the process on a few different numbers first.)
The ShiftCipher algorithm is a simple way of encrypting a word. Here’s how it works:
Take a word, such as DOOR. Shift the first letter once – D becomes E. Then, since D is the 4th letter of the alphabet, shift all the other letters 4 times – OOR becomes SSV. If at any point you hit Z and need to go past it, then just wrap back around to A. So, ShiftCipher(“DOOR”) = “ESSV”. (Another example: ShiftCipher(“EYES”) = “FDJX” – try it).
Write the DecryptShiftCypher algorithm.
Problems
You always set your alarm clock to wake you up one hour before you have to leave. But if you have to leave before 7 am, you give yourself 15 extra minutes to get ready since you know you’ll be groggy.
What’s the input for the process described above? What’s its output?
What time would you have to leave if the clock woke you up at 5:40am? 5:50am?
Your alarm wakes you up. Based on the time you see on the clock, how do you know when you’ll have to leave?
You’ve got a stack of five pancakes, all of different sizes. Your only tool is a spatula, and the only basic operation allowed is: insert the spatula beneath any pancake in the stack and flip the whole section of the stack that’s above the spatula onto the remaining stack below. Your job is to sort the stack so that the smallest pancake ends up on top and the pancakes increase in size as you go down the stack.
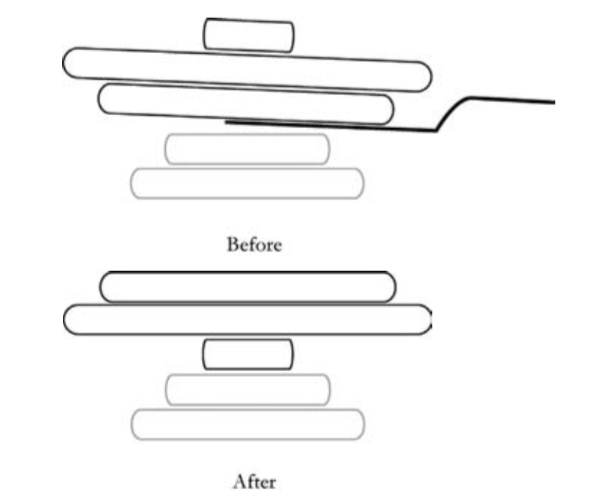
Sort each of the following stacks, using as few flips as possible.
Write a general algorithm for sorting any stack, and try it out on a few different initial arrangements of pancakes.
Make up a worst-case initial arrangement of five pancakes for your algorithm. How many flips does your algorithm take in the worst case?
You’ve lost your calculator, and your diabolical arch nemesis has decided to exploit this opportunity. He’ll make calculations for you — for a price! Multiplication costs $\$1$, whereas exponentiation costs $\$6$. Unfortunately, you desperately need to compute ${7^{10}}$, and you’ve only got $\$5$. What will you do?
You input any word, and the AlphaBlast algorithm outputs the same word but with all the ‘a’s replaced with ‘z’s. Is AlphaBlast reversible? Example: AlphaBlast(“mathematics”) = “mzthemztics”. Test it carefully and then explain your answer. (An algorithm is called reversible if it’s possible to create an inverse algorithm for it.)
For each of the following algorithms, assume that the input can be any number, and call it $X$. Read each description, and decide in each case whether the algorithm is reversible. If so, write the inverse.
The Foo algorithm either multiplies $X$ by 2 (if it’s a whole number) or doesn’t change it (if it’s not a whole number).
The Bar algorithm either multiplies $X$ by 2 (if it’s NOT a whole number) or doesn’t change it (if it IS a whole number).
The FractionsAreFun algorithm takes
The NoReallyTheyAre algorithm divides $X$ by 20 then adds 1 and outputs the result.
The Flip algorithm outputs the value of 100/$X$, unless $X$ is zero, in which case the output is just zero.
The Flop algorithm divides 20 by $X$, then adds 1 and outputs the result.
The Square algorithm simply outputs the value of ${X^2}$.
Here’s a variation on the Number Devil game: the Number Devil is allowed to change its secret number after each time you guess. However, it can’t change it in a way that makes any of its previous answers untrue. (So, if you guessed “5” the first time and the answer was “higher”, it could not change its answer to “2”, but it $could$ change it to “7”.)
Explain why binary search algorithm’s worst-case guarantee is still the same.
Describe an algorithm the Number Devil could use to force a worst-case outcome every time, as long as you didn’t get lucky and guess right the first time.
Here’s a tougher variation of the game you played in problem 8. The setup is the same: your partner shuffles the cards and lines them up, and you can’t look at them. But now, instead of just finding the largest one, your goal is to sort all the cards into descending order (i.e., line them up from largest to smallest). Your basic operations are (i) to ask your partner to compare two cards (just like last time), and (ii) to swap the positions of any two cards.
Write an algorithm for this game. That is, create an algorithm that will sort a list of 5 numbers. After writing the algorithm, go ahead and try it out with a group member. Does it work?
Look back at your pancake-flipping algorithm from problem 34. If you extended your algorithm to stacks of $N$ pancakes, how many flips, maximum, could you guarantee it taking — that is, what’s the worst it could do?
Here’s a different version of the pancake problem. This time, you have three plates. Plate #1 has a stack of 5 pancakes, in order from the largest one on the bottom to the smallest on top. This time, though, you can only use the spatula to shift one pancake at a time to another plate. At no time can any larger pancake be on top of a smaller pancake. How many moves does it take to get the entire stack of pancakes from Plate #1 to Plate #3?
Don’t use a calculator for this problem.
Simplify $\frac{{20{a^4}{b^7}}}{{30{a^3}{b^{ - 2}}}}$
Reduce the fraction $\frac{x^3 +2x}{x^2 + x}$
Solve for $x$: ${x^{\frac{2}{3}}} = 64$
Solve for $x$: ${x^2} + 8x + 9 = 0$
Solve for $x$: $3{x^2} + 7x + 3 = 0$
If you double the size of a list in which you’re doing a binary search, will it (in the worst-case scenario) take you about twice as long to do the search?
The shape below is called a “tromino.”

Each of the following “checkerboards” has had one square removed. For each board, find a way to cover all of the remaining squares with trominoes.




You have only a compass and an unmarked straightedge. Come up with an algorithm for finding a point equidistant from three given points. In doing so, you will have proven that it is always possible to find such a point.
Alice is in the top right square of a giant chessboard, and the white rabbit she’s chasing is in the bottom left square. Each turn, Alice gets to move one square up, down, left, or right. Then, after that, the white rabbit gets to move (up, down, left, or right). Alice catches the rabbit when she’s able to move into the square he’s sitting in. Assuming that both Alice and the white rabbit are strategically quite savvy, predict the outcome.
The Floor operation takes any number whatsoever as an input. ${\mathop{\rm Floor}\nolimits} (x)$ simply takes $x$ and returns the greatest integer that’s less than or equal to $x$. In other words, the Floor function always “rounds down.” Examples: ${\mathop{\rm Floor}\nolimits} (2.001) = 2$, $\mathrm{Floor}(\pi ) = 3$, and $\mathrm{Floor}(5.9999)=5$.
The following algorithm, which uses Floor and some basic arithmetic operations, only takes positive integers for its input. What does it do?
${\mathop{\rm Mystery}\nolimits} (n) = 5\left( {\frac{n}{5} - {\mathop{\rm Floor}\nolimits} \left( {\frac{n}{5}} \right)} \right)$
The RightShift and LeftShift operations work for any non-negative integers with five or fewer digits:
${\mathop{\rm RightShift}\nolimits} (N,d)$ chops off the rightmost $d$ digits of $N$ and outputs the result. Example: ${\mathop{\rm RightShift}\nolimits} (3214,2) = 32$.
${\mathop{\rm Left}\nolimits} {\mathop{\rm Shift}\nolimits} (N,d)$ moves each digit $d$ places to the left, and fills in 0’s in the empty spaces; then, it chops off all but the last five digits. Examples: ${\mathop{\rm Left}\nolimits} {\mathop{\rm Shift}\nolimits} (75,3) = 75000$, and ${\mathop{\rm Left}\nolimits} {\mathop{\rm Shift}\nolimits} (3214,2) = 21400$.
Starting with the number 6789, how can you use only the LeftShift and RightShift operations to end up with the number 7?
Generalize your work from part a to create the PickADigit algorithm, where ${\mathop{\rm PickADigit}\nolimits} (N,d)$ outputs the $d$th digit of a positive integer $N$.
What does the following algorithm do, assuming that $N$ is a positive, five-digit integer?
$$\begin{split}\rm{Ffleba}(N) &= \rm{LeftShift}(N,2) \\ &+ 10 \cdot \rm{RightShift}(N,4) \\ &+ \rm{RightShift}(\rm{LeftShift}(N,1),4) \end{split}$$You input a whole number to a certain algorithm. If it’s even, the algorithm doesn’t change the number. If it’s odd, the algorithm turns the number backwards — for example, 57 becomes 75. Is this algorithm reversible?
Come up with a non-trivial numerical
algorithm that reverses itself. In other words, come up with
an algorithm Boing such that, for every $N$,
$\text{(Boing(Boing}(N))= N$.
Imagine your friend gave you a very long table of $all$ the possible inputs to her algorithm and their corresponding outputs. Even if she didn’t explain the process her algorithm used, describe using a single sentence how you could figure out whether or not the algorithm was reversible.
Your basic operations for the following are addition, subtraction, multiplication, division, and testing which of two numbers is the biggest.
Write an algorithm for figuring out whether or not a positive integer $N$ is prime. Pick some three-digit numbers and try it out. (By the way, computer systems actually use algorithms like these to encrypt your private data.)
Suppose it takes you 3 seconds to use your calculator to do each of the basic operations above. How long would it take you to check whether or not 1,000,003 is prime? How about 1,000,005?
You have 4 identical-looking coins. Two of them are heavy and two of them are light (the two heavy ones weigh the same, and the two light ones weigh the same).
Call the coins A, B, C, and D. Your goal is to find out which two are heavy and which two are light. Your only instrument is a balance scale — you put some coins on the two sides of the scale, and it tells you which side is heavier (or that the two sides weigh the same).
Describe an algorithm for finding the light coins in as few steps as possible.
When you type a text message into a cell phone using multi-tap typing, you are essentially encoding English words into a long sequence of numbers (and pauses). For example, to type in the word “EIGHT”, I type: 3 3 4 4 4 [pause] 4 [pause] 4 4 8. Use this picture of a cell phone’s keypad to help you:
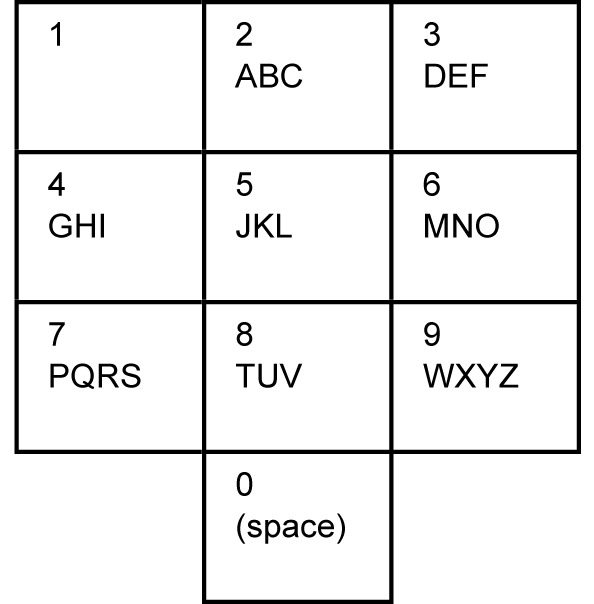
I typed 7 7 7 7 , 7 3 3 , 3 3 2 2 2 4 4. (Here the commas represent pauses). What word did I type?
Write an algorithm for “decoding” a string of numbers and pauses into a word.
You and a fellow explorer need to be able to communicate two numbers to each other — coordinates for your location, which will always be positive whole numbers, but can be small or large. The only means of communication you have is a carrier pigeon. Due to its tiny brain, the pigeon can only remember one $whole$ number (though it can be as big as you want).
Somehow, you need to fit the two numbers together into one number, but you need to make sure that the process is reversible, so that your companion can figure out what numbers you’re sending him.
Here’s the first process you try. Say your two numbers are 67 and 302. Then you just put them together to make 67302, and send that number along with the pigeon.
Why is this non-reversible?
The next strategy you develop fails as well. What you tried to do was separate the numbers with “000”. So, 67 and 302 gets written as 67000302.
This strategy will usually work, but not for every pair of numbers. When is this strategy non-reversible?
Create your own strategy, and show that it works — that it is reversible.
Exploring in Depth
Look back at the sorting algorithm you wrote for problem 39.
Are there certain initial arrangements of the cards that make your algorithm finish in fewer steps?
Using your algorithm, what’s the maximum number of comparisons you have to make, in the worst case, when you play the game with five cards?
If you used your sort algorithm from problem 39 to sort a list with $N$ items in it, how many comparisons would it take? See if you can express your answer as a simple algebraic formula.
Five pirates come across 100 bars of gold. The pirates have a pecking order, with #5 and #1 indicating the top and bottom-ranked pirates, respectively. Each pirate wants to maximize his or her share of the gold bars. There are no coalitions or collusions between them. They are all very analytical — they can think things through!
Their process for splitting the loot is somewhat democratic. It begins with the top-ranked pirate making a proposal on how to divvy up the loot. (Note that the gold bars cannot be broken up, glued together, or otherwise changed; there are 100 bars of gold, period.) Each pirate gets one vote, up or down on the entire proposal. Remember, each pirate votes based on his or her own pocket and there are no side agreements of any sort. If the proposal gets 50% or more votes, it wins, and that’s that. On the other hand, if it fails to muster 50%, then the pirate who made the proposal is thrown overboard, and the process continues with the next pirate down the hierarchy.
What is the maximum number of bars that the most powerful pirate can get and what allocation to each pirate will ensure him the 50% vote that he needs?
(from http://www.eogogics.com/talkgogics/ezine/tech-talk/pirates1)
Create an algorithm to find the median of a list of numbers. Your only basic operation allowed is to compare two numbers to see which is larger. Assume the list has an odd number of items in it.
Write an algorithm that finds the second largest number in a list of 16 numbers, using only comparison as the basic operation. It’s possible to guarantee a correct answer in fewer than 29 comparisons — can your algorithm do this?
Sherlock and Watson create the following code to encrypt their messages:
First, turn each letter into a number (A is 1, B is 2, etc). Then for each number, multiply it by 7 and add 1. Finally, if any numbers have 3 digits, just ignore the hundreds digit — so 141 just gets written as 41, and so on.
Encrypt the word NO according to their code.
Sherlock sends Watson the message 36 34 22 8 13 36. Decode it.
Even though the code "erases” hundreds digits, it’s still perfectly reversible — you can always decode any message and know exactly what was written. Explain why it’s reversible.
You create an especially tricky locker code. Here’s what you do to encode the 3-number combination: The new first number will be the sum of all three numbers in the original.
The new second number will be the sum of the first two numbers in the original.
The new third number will be the sum of the last two numbers in the original.
Encode 12 – 8 – 1. Do you see how you could find the 12, 8, and 1 from the coded version?
Decode 17 – 14 – 5.
You receive a coded combination:
This is a famous problem that’s challenged many mathematicians. You have 12 coins that look alike. 11 are genuine and each have the same weight. 1 is counterfeit, and is $either$ too heavy or too light.
Write an algorithm for how to use a balance scale to find the fake coin, $and$ determine whether it’s too heavy or too light, in as few steps as possible. (It can be done with three weighings! See if you can figure out how.)
Hint: it will probably help a lot to make a chart to keep track of the different possibilities.