Introduction
The following tree diagrams, which are called binary trees, are all based on the same system for organizing information.
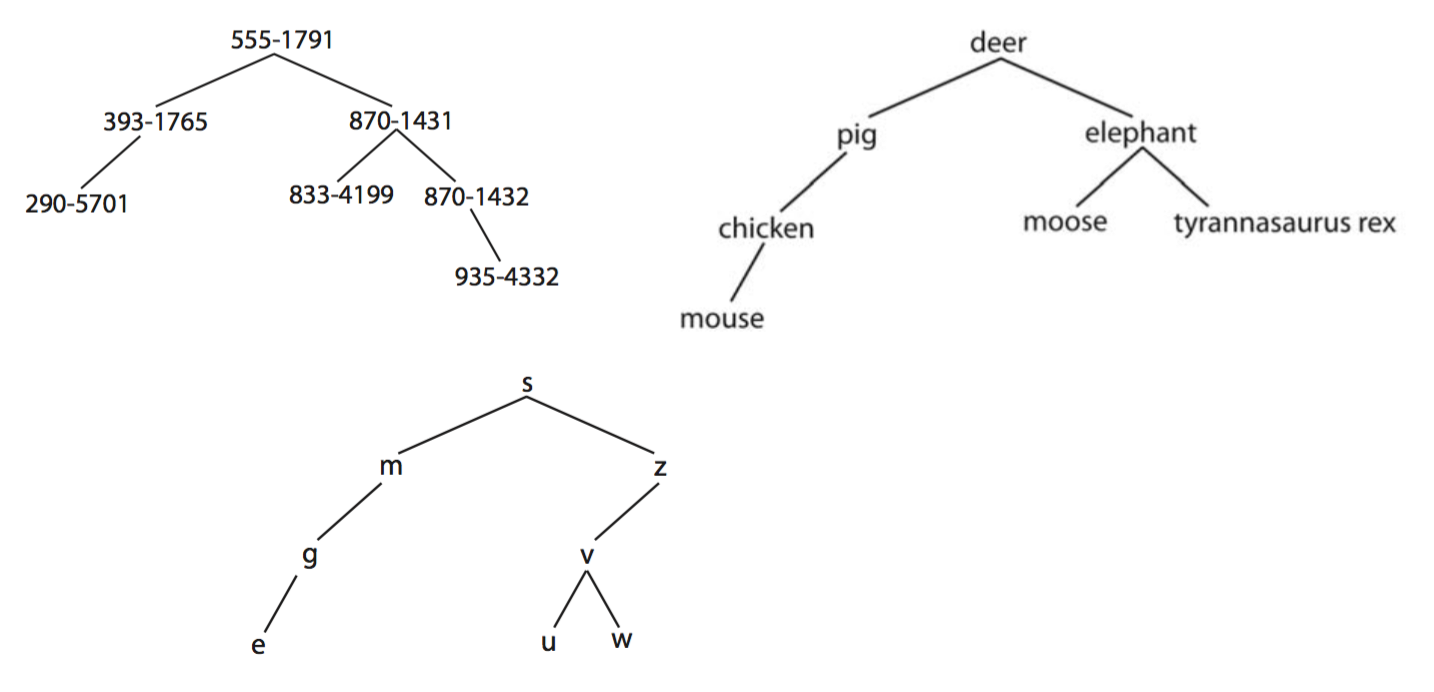
Each item (phone number, animal, letter) in the tree is called a “node”, and the nodes immediately below a node are called its “children”. As you can see, each node in the tree has at most two children. Furthermore, notice that as you start at the top and travel down the branches, every descendant down the right branch of a given node is somehow more than (or larger than, or after) that node, whereas every descendent to the left is somehow less.
Let’s say we wanted to add the number “866-3162” to the phone number tree above. Even though it comes after “393-1765”, it would be wrong to hang it to the right of that number, because that would still be down the left branch from “555-1791”. Where should “866-3162” go? How about “squirrel” and “k” in their respective trees? There is only one correct answer for each of these.
Ask a group member to write down, without showing you, a list of 10 different numbers. Your group member will be reading the list to you one number at a time, and your job is to organize them into a binary search tree as they’re being read to you. There’s one rule: unlike in nature, these trees grow down. This means, for example, that the first number your group member reads will have to be the one at the very top of your tree.
Have your group member read the numbers to you, giving you time to add each number to the tree, without rearranging the ones you’ve added so far, before reading the next one out.
What would have happened if the numbers had been read to you in a different order? Try it and see.
In these small examples, it’s quite easy to see all the information at once, so they’re not necessarily any better than just writing out a simple list. Imagine, though, that instead of the 7 phone numbers in the first diagram, you had a binary tree with hundreds of phone numbers in it. (By the way, this is essentially how a cell phone really does store phone numbers.)
Alice the ant starts at the top node of this large phone number tree and wants to know if the exterminator’s number, which she knows by heart, is in it. (She’s hoping it’s not!) Because Alice is so small, she can only read one node at a time, and she has to crawl down a branch to read another number.
Describe a simple algorithm she can use to find out where the exterminator’s number would have to be, if it were in the tree.
Which of the following trees do you think Alice would rather search? Remember the old saying: when you’re trying to find something, it’s always in the last place you look!

Development
You saw from problem 2 that there is more than one possible “shape” that a binary tree can take, even with the same raw data.
For each of the following, come up with a sequence of items, which, if you used your approach from problem 2, would end up in a binary tree with the given shape. (The items can be anything you want: names, numbers, etc.)



The depth of a node in a tree is the number of branches it is away from the top. So, for example, “chicken” in the animal tree has a depth of 2. The depth of the whole tree is just the depth of its deepest node. (So the animal tree has a depth of 3, because “mouse”, the deepest node, has a depth of 3.)
Rearrange the lists of items you used in problem 4 so that the resulting trees have the minimum possible depth.
Do the same for the list your group used in problem 2.
The trees you made in problem 5 are examples of balanced binary trees, whereas the one you made in problem 6 is not balanced. To see why, think of the tree like a hanging mobile: if each node is perfectly balanced, then the whole thing is balanced.
Is it possible to arrange the numbers 1 through 7 into a balanced binary tree? How about 1 through 12? 1 through 15?
A leaf of a tree is a node that doesn’t have any children. Notice that in a balanced binary tree, all the leaves have the same depth. If a balanced binary tree has 512 leaves, then what is the depth of the tree?
Of course, not all trees have to be binary. If you continued the regular pattern of the tree below, how many leaves would the next level of the tree have? How deep would it need to be in order to have 4096 leaves?

On some ancient computers, passwords had to consist of only the letters A through E. If I tell you that on these computers, there were 15625 passwords, and all of the passwords had to be the same length, can you say how many letters were required in a password?
In the last three problems, you were effectively looking for exponents. You might have found yourself asking, in rather awkward English, the question:
\[ \text{5 to the } what \ power \text{ equals 15625?} \]
Fortunately, there’s a mathematical term for the number
we’re looking for here: it’s called “the logarithm, base 5, of
15625”. Symbolically, it’s written
So our awkward question is now both easier to pronounce:
$$\rm{What \; is \; the \; log, base \; 5, of \; 15625?}$$
and easier to write:
$$\log_5 (15625)=x.$$
Translate the equation above into an equation involving exponents.
Go back and set up problems 8-10 with equations using log notation. (No need to solve them again—just set them up.)
Use symbols to create a formal definition for what it
means to say that
This is something you can refer to whenever you need to translate to and from “log” notation.
Practice
Consider the following binary tree.

Assuming this tree was built similarly to the one you built in problem 2, what order could the letters have been added in?
What ordering would you use to produce a tree with the greatest possible depth?
Determine the depth of each of the trees described below.
A balanced binary tree that has 1,048,576 leaves.
Every node that isn’t a leaf has 4 children. There are 64 leaves.
Every non-leaf node has 6 children, and there are $X$ leaves. (Answer in terms of $X$, using log notation.)
Unlike on this planet, primordial amoebas from Mars reproduce by splitting into three children. If life on Mars started with a single amoeba, but now there are 1,594,323 amoebas, then:
Estimate, without using a calculator, for how many amoeba-generations there has been life on Mars.
Now rewrite the question as a logarithm, and find an exact answer (calculator allowed this time).
Translate the following awkward bits of English into log notation. (Notice that some are complete sentences, and others are fragments.)
“What number could I raise 4 to, to get 64?”
“The power of 3 that gives you 81”
“4 to the something-or-other power equals 1024.”
“The number to which 6 must be raised in order to produce 216”
“The number of times, starting with
1, that you have to double to
Calculate the value of each of the following:
${\log _3}\left( {81} \right)$
${\log _{13}}\left( {169} \right)$
${\log _8}\left( {512} \right)$
${\log _{11}}\left( {14,641} \right)$
${\log _{100}}\left( {1,000,000} \right)$
${\log _{1,000}}\left( {1,000,000} \right)$
${\log _{10}}\left( {1,000,000} \right)$
${\log _{15}}\left( {11,390,625} \right)$
Going Further
Start with $x = 243$. Check with your calculator that ${\log _3}\left( x \right) = 5$. How much do you have to add to $x$ to make ${\log _3}\left( x \right)$ go up by one? Up by two? Three?
What is the value of ${\log _9}\left( 3 \right)$?
Since the number 3 is not one of the powers of 9, it’s not clear just what this question means, or how to find out what the value of ${\log _9}\left( 3 \right)$ would be. Remember, though, that it’s also possible to have non-integer exponents. Let’s see if we can use that to find an answer.
Start by rewriting ${\log _9}\left( 3 \right) = x$ in exponential form. Then, try tinkering with different ways to write this equation by applying some of your rules of exponents.
You might have noticed in the problem above that it was much simpler to solve once you’d rewritten “3” as “${9^{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}}$”. In the next problem, try using a similar strategy: tinker with different ways of rewriting things, using the definition of logarithms and your exponent rules. (You might want to take a minute with your group to remind yourselves of all the rules.)
Find the value of each of the following without using a calculator.
${\log _4}\left( {32} \right)$
${\log _5}\left( {\frac{1}{{25}}} \right)$
${\log _{10}}\left( {0.000000001} \right)$
${\log _7}\left( 1 \right)$
Why can you be sure that ${\log _2}\left( {42} \right)$ is not an integer?
Find every number from 1 to 1 million whose base-10 logarithm is an integer.
The “log” button on your calculator actually stands for “${\log _{10}}$”.
Before trying it out, can you estimate roughly what ${\log _{10}}\left( {4000} \right)$ will be? Check it on the calculator.
What are ${\log _{10}}\left( {40} \right)$, ${\log _{10}}\left( {40,000} \right)$, and ${\log _{10}}\left( 4 \right)$? What’s the pattern?
Pick several three-digit numbers, and use your calculator to find the base-10 log of each one. Now do the same with several four-, five-, and six-digit numbers. What do you notice?
If ${\log _{10}}\left( 2 \right) = 0.301$, then what is the value of ${\log _{10}}\left( {2 \cdot {{10}^a}} \right)$?
If you want to see why your answer to the previous problem is true, try using the definition of log and your exponent rules to tinker with different ways of rewriting things, like you did earlier in problems 20-22. This will also help with the next two problems.
If ${\log _2}\left( x \right) = 1.125$ and ${\log _2}\left( y \right) = 2.875$, then what is the value of ${\log _2}\left( {x \cdot y} \right)$?
If ${\log _4}\left( x \right) = 1.20$ and ${\log _4}\left( y \right) = 2.009$, then what is the value of ${\log _4}\left( {x \cdot y} \right)$?
Practice
Put the following in order from least to greatest:
${\log _2}(47)$, 2, ${\log _3}(47)$, 3, ${\log
_2}(35)$, $4$, $\log_4(100)$, $5$, ${\log _3}(240)$.
What are the nearest integers above and below ${\log _2}\left( {24} \right)$? Which of the two is the closest?
Find the value of each of the following.
${\log _{16}}\left( 4 \right)$
${\log _3}\left( {\frac{1}{9}} \right)$
${\log _4}\left( {.5} \right)$
${\log _2}\left( {\sqrt 2 } \right)$
Why does your calculator give you an error when you input
Practice using the definition of logarithms and the rules of exponents to solve each of the following.
If ${\log _4}\left( x \right) = 1.6$ and ${\log _4}\left( y \right) = 3.2$, then what is ${\log _4}\left( {xy} \right)$?
If ${\log _8}\left( x \right) = 6$, then what is ${\log _8}\left( {2x} \right)$?
Problems
If ${\log _5}\left( x \right) = 5$ and ${\log _5}\left( y \right) = 7$, then what is the value of ${\log _5}\left( {\frac{y}{x}} \right)$?
If ${\log _3}\left( x \right) = 1.776$ and ${\log _3}\left( y \right) = 2.018$, then what is the value of ${\log _3}\left( {\frac{y}{x}} \right)$? (By the way: how old is the United States of America?)
Based on what you did in problems 28 and 29, complete the following generalization: “If ${\log _b}\left( x \right) = C$ and ${\log _b}\left( y \right) = D$, then ${\log _b}\left( {xy} \right) = $….” Now prove it using algebra.
Revise the generalization you wrote in the previous problem into an identity that relates ${\log _b}\left( {x \cdot y} \right)$ to ${\log _b}\left( x \right)$ and ${\log _b}\left( y \right)$. (Remember that an identity is just an equation that is always true, for all values of the variables involved.) This identity is going to come in handy, so write it down somewhere where it will be easy to refer to it.
Given that ${\log _2}\left( 5 \right) = 2.322$ and ${\log _2}\left( 3 \right) = 1.585$, what is the value of ${\log _2}\left( {15} \right)$?
State and prove an identity that relates ${\log _b}\left( {\frac{x}{y}} \right)$ to ${\log _b}\left( x \right)$ and ${\log _b}\left( y \right)$.
If ${\log _3}\left( {10} \right) = 2.096$, then what is the value of ${\log _3}\left( {30} \right)$? How about ${\log _3}\left( {100} \right)$?
Don’t use a calculator for this problem.
Simplify $16^\frac{1}{2} \cdot 2^3$.
Simplify $\frac{{{x^5}{y^{ - 3}}}}{{{x^{ - 1}}{y^2}}}$.
Solve for x: $4x^3 + 2x^2 = 0$.
Simplify $\frac{{\sqrt {125} }}{{\sqrt {50} }}$.
If $\frac{1}{{{x^2}}} - \frac{1}{x} = 1$, find ${x^2} + x + 1$.
What is the value of ${\log _2}\left( {{4^{1005}}} \right)$?
For each of the following equations, use the log function of your calculator (and possibly some algebra) to approximate $x$ to the nearest thousandth.
${10^x} = 461.2$
$3 \cdot {10^x} = 5$
${10^{x + 2}} = 50$
Mr. Golthramis was in a bad mood one day, and decided to take it out on his students by giving them this problem: “Write down, using no exponents, a number $x$ such that $\log_{10}(x) > 1000$.” The students, having recently learned the definition of log, were outraged, and refused to do the homework. Why?
Verify with your calculator that ${\log _3}\left( {12} \right) = 2.2619$. Now, find the values of $\log_3 (36)$ , ${\log _3}\left( 4 \right)$, and $\log_3 (108)$.
According to the incomplete table below, ${\log _5}\left( {10} \right) = 1.4307$. Is this (approximately) correct? Correct it if not, and then complete the rest of the table.
| A | ${\log _5}\left( A \right)$ |
| 2 | |
| 0.5 | |
| 4 | |
| 1 | |
| 8 | |
| 10 | 1.4307 |
| 16 | |
| 2 | |
| 2.1535 | |
| 50 |
Suppose we visualize some number $L$ as a tree diagram with
$L$ leaves, and another number $M$ as a tree with $M$ leaves.
Using these as building blocks, how could you build a tree to
visualize the quantity
Consider a balanced binary tree with a depth of $D$.
True or false: the total number of nodes in the tree will be $1 + 2 + {2^2} + ... + {2^D}$.
Find a simple formula for the total number of nodes in the tree. Answer in terms of $D$, and without using “…”. (Hint: try several small examples, and look for a pattern.)
If a balanced binary tree has 1023 nodes total, then how many of the nodes are leaves?
Have one of your group members make up a binary tree and show it to you. Your job is to add nodes to the tree until you have doubled the total number of nodes, while keeping the tree as “shallow” as possible. Try this a few times with trees of different sizes and shapes. If the original tree has $N$ nodes, then how many additional levels of depth do you need?
If you build a binary tree by adding the numbers 5, 2, 3, 7, 11, 17, and 13, in that order, the resulting tree would not be balanced. (Check this.) Instead of this, suppose you put these seven numbers into a hat and randomly chose one number at a time to add to the tree. What is the probability that your tree would be balanced?
Prove that each of the following are true:
${\log _b}\left( {{x^2}} \right) = 2 \cdot {\log _b}\left( x \right)$
${\log _b}({x^3}) = 3 \cdot {\log _b}(x)$
${\log _b}\left( {{x^4}} \right) = 4 \cdot {\log _b}\left( x \right)$
${\log _b}\left( {{x^5}} \right) = 5 \cdot {\log _b}\left( x \right)$
Use the rule you just proved in the previous problem to solve each of the following for $x$, and give your answer to the nearest thousandth. (Hint: $A = C$ if and only if ${\log _b}A = {\log _b}C$.)
${1.02^x} = 2$
${2^x} = 1000000$
${1.5^{x - 3}} = 21$
What is ${\log _{10}}\left( {{{\log }_{10}}\left( {{\mathrm{one \, googol }}} \right)} \right)$? What is ${\log _{10}}\left( {{{\log }_{10}}\left( {{{\log }_{10}}\left( {{\mathrm{one \, googolplex}}} \right)} \right)} \right)$?
(If you don’t know what a “googol” or “googolplex” is, Google them.)
Professor Arlo G. Smith poses the following questions:
What is the ratio of ${2^9}$ to ${2^5}$? What is the ratio of ${2^m}$ to ${2^n}$?
What is the ratio of $\log {2^9}$ to $\log {2^5}$? What is the ratio of $\log {2^m}$ to $\log {2^n}$?
What is the ratio of $100000000$ to $1000000$? What is the ratio of $\log 100000000$ to $\log 1000000$?
If:${\log _b}\left( X \right) = 3 \cdot {\log _b}\left( 2 \right) + 2 \cdot {\log _b}\left( 3 \right) + {\log _b}\left( 5 \right)$ then what is $X$?
Rewrite the expression ${\log _5}7 + {\log _5}15 - {\log _5}3$ as a single logarithm in the form ${\log _b}a$.
Not all calculators have a built-in way to calculate ${\log _2}\left( {47} \right)$. However, using the definition and properties of logarithms, there is a way to figure this out with any scientific calculator. Here’s a hint: re-write ${\log _2}\left( {47} \right) = x$ in exponential form, and then solve for $x$.
Can the ${\log _{10}}$ of an irrational number minus the ${\log _{10}}$ of a different irrational number ever equal a positive integer? Explain.
Solve each of the following equations, giving your answer to the nearest thousandth.
${1500 \cdot {1.13^t} = 4000}$
$3 \cdot {5^{x + 5}} = 8$
${\log _3}x - 2{\log _3}7 = 1$
${5^{x - 1}} = {2^{3x - 1}}$
$7 \cdot {x^3} = 1492$
A binary tree has 6000 nodes in it. What are its minimum and maximum possible depths?
Recall the Number Devil guessing game from the previous lesson, where the Number Devil picks a number between 1 and 15 and you have to guess it. When you guess, the Number Devil will tell you whether you’re correct, too high, or too low. If you use binary search, how many guesses will you need in the worst case? What if the Number Devil chose a number between 1 and 1 million?
That pesky bad coin you saw in the previous lesson is back. (Maybe the Number Devil brought it along.) You have 27 identical-looking coins. The bad coin is too light, and the rest all weigh exactly the same.
Using a balance scale, how many weighings do you need to find the bad coin?
How many weighings would it take to find one bad coin among 2187 coins? How about 1 million coins?
If you look up logarithms on the Web, you’re likely to see the following sentence, which is meant to be a helpful reminder when you’re learning what logarithms are:
“A logarithm is an exponent.”
What do you think people mean by this?
If $a_1,a_2, a_3, \ldots$ is a geometric sequence, then what kind of sequence is $\log_b(a_1), \log_b(a_2), log_b(a_3), \ldots$?
Recall that the Floor operation from the previous lesson takes a positive number $x$ and chops off anything after the decimal point. Similarly, the Ceiling function essentially “rounds up”: e.g., ${\mathop{\rm Ceiling}\nolimits} \left( 3 \right) = 3$, and ${\mathop{\rm Ceiling}\nolimits} \left( {2.0001} \right) = 3$. If $N$ is a positive integer, what does ${\mathop{\rm Ceiling}\nolimits} \left( {{{\log }_{10}}\left( N \right)} \right)$ tell you about $N$?
If you double a three-digit number 100 times, how many digits will the resulting number have?
Prove that squaring a number at most doubles the number of digits in the number.
Prove that ${\log _b}\left( {\frac{1}{x}} \right) = - {\log _b}\left( x \right)$.
Generalize what you did in problem 59 into an identity about logarithms.
What is ${\log _{10}}\left( 2 \right) \cdot {\log _2}\left(
{10} \right)$?
How about ${\log _{10}}\left( 3 \right) \cdot {\log _3}\left(
{10} \right)$?
And
In a balanced ternary tree, every non-leaf node has three children, and all the leaves have the same depth. How many nodes are in a balanced ternary tree with a depth of 10?