Introduction
An ecologist is studying moose herds, to see if hunting practices are depleting the herds. In each herd, every year, $\frac{1}{3}$ of the population reproduces (1 baby moose each). Every fall, though, after the moose reproduce, hunters are allowed to hunt down 100 moose. In one herd, at the beginning of the study there are 270 moose. What would be the size of the herd population after 5 years? (Each year, round to the nearest moose.)
The situation above is an example of recursion — a process in which the input at any particular stage depends on the output of a previous stage (or previous stages). In this particular case the size of the herd in any given year is dependent on its size the year before.
If you understand exactly how the stages are related you can then express that relationship with an equation, called a recursive equation. These equations will allow you to model and track changes in all sorts of populations — people, wildlife, bacteria, viruses, radioactive material and a host of others. People who use these powerful tools are interested in essentially three important questions: Will the population continue to increase without bound, will it level off at a certain number, or will it disappear after a certain period?
Here is another example of a recursive process.
Enter any number greater than 1 in your calculator and find its square root. Then find the square root of your answer. Continue finding square roots of previous answers until something interesting develops. Do you think the same thing would happen with any number greater than 1 that you choose? How about any positive number less than 1?
Development
A bacteria colony is placed into a Petri dish along with a bacteria-eating fungus. Every day, the bacteria population increases by 50%, but during the night at midnight, the fungus devours 50 bacteria.
Draw a chart and track the bacteria population over the next week, if the initial population is 120:
|
# days later |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
Pop. size |
120 |
A smaller colony would have a hard time surviving in the same dish as the fungus. Find an initial population size that would cause the population to drop quickly. Draw a chart for this situation. You can assume that if at the end of a day there are less than 50 bacteria left, the fungus will simply eat all the bacteria that are left.
Find an initial population size that would cause the population to decline slowly. Draw a chart for this situation.
Is there a population size that would remain unchanged despite the bacteria-eating fungus? (In this sort of outcome, the system is said to be in a state of equilibrium, or in a steady state.)
Explain how you could figure out ${B_n}$, the number of bacteria after n days, by knowing the population in the dish one day earlier. Write an equation for ${B_n}$ in terms of ${B_{n - 1}}$.
Is there a number such that if the population size falls below that number, the colony will eventually die out?
The equation you wrote in problem 3e is a recursive equation. To fully describe a recursion process one would write the recursion equation together with the initial condition. In the case of problem 3e, for example, we would write ${B_n} = \frac{3}{2}{B_{n - 1}} - 50$ as well as ${B_0} = 120$. In mathematics, the subscript zero is sometimes used to represent the amount or number you started with.
A buyer and seller are bargaining over the price of an antique lamp. First, the buyer offers to pay $\$400$. Next, the seller makes a counter-offer — she’ll sell it for $\$800$. Trying to be fair, the buyer decides to average those two prices for his next offer of $\$600$. Also trying to be fair, the seller then averages the two most recent prices, to make her next offer. They continue bargaining, each using the averaging method to come up with their next offer.
Draw a table like the one below with the prices offered and fill it out.
| Buyer | 400 | |||||||||||||
| Seller | 800 | |||||||||||||
Let $\{ {L_n}\} $ be the sequence of prices that are offered (disregarding who makes which offers). So, since the buyer makes the first offer of $\$400$, and the seller then offers $\$800$, ${L_1}$=400 and ${L_2}$=800.
What is ${L_5}$?
Which offers would you need to know, in order to find ${L_{100}}$? Write an equation for ${L_{100}}$ in terms of those offers.
Write a recursive equation for ${L_n}$, in terms of the previous offers.
Who seems to be at an advantage in this situation — that is, who is happier with the prices being offered?
Is there a point at which this bargaining process would stop? Assume that payment will be made in whole dollars.
Write a recursive equation to describe the process in problem 2.
When students were asked to create their own recursive problem, Emdash came up with the following;
${G_{n + 2}}\,\, = \,\,\frac{{{G_{n + 1}}}}{{{G_n}}}$, ${G_1}$= 2. Find the first nine terms of the sequence.
It is not possible to solve Emdash’s problem. Why?
Vasilla added to Emdash’s problem the following: ${G_2}$= 4. Is it possible to write down the first nine terms of Vasilla’s sequence?
Practice
You are training for a race by running every day. On the first day, you run 2000 meters. Every day after that, you increase the past day’s run by 20%, and then add on an extra 100 meters.
Fill in the chart with how much you run each day:
|
Day |
1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
Distance |
2000 |
Write a recursive equation for ${R_n}$, the distance you run on day $n$.
Back to our moose situation in problem 1 in which every year $\frac{1}{3}$ of the population reproduces (1 baby moose each), and every fall hunters are allowed to hunt down 100 moose, but only after the moose reproduce. (This time you do not have to round to the nearest moose each year.)
In one herd, at the beginning of the study there are 270 moose. Write a recursive equation for ${M_n}$, the population of the moose herd after n years. What do you think will ultimately happen to the population of this herd?
Suppose at the beginning of the study there were 310 moose. What would be size of the herd after 5 years? What do you think will ultimately happen to the population of this herd?
Another herd’s population is in an equilibrium state — it doesn’t ultimately grow or shrink. What was its starting population? Explain why this herd’s population doesn’t change.
Refer to problem 4, where a buyer and seller are trying to agree on a price for a lamp. Recall that each new offer was the average of the previous two offers. Again let $\{ {L_n}\} $ be the sequence of prices that are offered (disregarding who makes which offers). But now suppose that the seller offers first. In this case ${L_1}$=800 and ${L_2}$=400.
What is ${L_5}$?
Who seems to be at an advantage in this situation — that is, who is happier with the prices being offered?
What price do you think they will settle on?
Why is the final price they agree on different, depending on who offers first?
A sequence follows a recursive rule — every term is 9 more than half of the previous term.
If the first term ${T_1}$ is 12, find the next 10 or so values of the sequence.
Do the same thing for different values of ${T_1}$— try some small numbers, and some large numbers.
What would ${T_1}$ have to be in order to produce an equilibrium solution?
For which values of ${T_1}$ does the sequence increase? For which does it decrease?
Problems
Sweden and Croatia are locked in an escalating arms race. Every year, one of the countries builds some bombs and missiles, and then inevitably, the next year, the other country builds even more to compensate. In each country, the Department of Defense has the following strategy:
For every new bomb that the enemy built last year, we’ll build 2 new bombs. For every new missile that the enemy built last year, we’ll build 2 new missiles, AND a new bomb.
Neither country can afford the expense of this pointless arms race, and each one claims that the other country started the whole situation by building the first few weapons.
In 2008, Sweden built a total of 64 new bombs and 16 new missiles. What will happen in 2009? How about 2010?
Those 64 bombs and 16 missiles were constructed in response to the weapons that Croatia built in 2007. What were those weapons?
Continue working back in time to determine who must have started the situation. What year did it start, and what weapons were built?
The fractal you see below is called the Koch Snowflake.
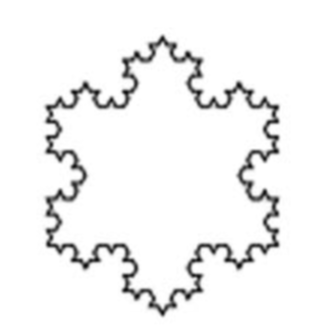
It’s a fractal because if you magnify any portion of the diagram, it will look like the diagram itself — also called self similar. The image you see above is actually just an approximation to the Koch Snowflake, but one could define the snowflake recursively. First, start with an equilateral triangle. Let’s call that stage 0.
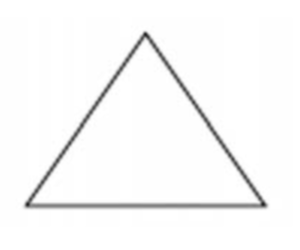
For the first iteration, stage 1, the middle one-third of each side is erased and two line segments — whose lengths are equal to the length of the erased segment — are added to form sides of smaller equilateral triangles. In the second iteration, the process is repeated. Each old segment is replaced with four new segments, each of which is one-third as long as the segment they replace. (See figure below)

Draw stages 1 and 2 of the snowflake. Be sure to use a pencil since at each step there’s some erasing to do.
Problem continued on the next page
Draw stage 3 of the snowflake.
How many stages do you think were completed for the image you saw at the beginning of this problem?
In problem 12:
If the length of each side of the original triangle is 1 unit, write a recursion equation for ${P_n}$, the perimeter of the shape after $n$ stages. Will the perimeter ever reach 1,000,000 units?
Suppose that the area of the
original triangle was
Write a recursive equation for
${A_n}$,
the area of the shape after $n$ stages. Could the area get as
large as
2000 people are exposed to a particularly contagious cold virus. Every day, $\frac{1}{4}$ of the people (rounded to the nearest person) that were healthy the day before, have now caught the virus. ${I_t}$ is the total number of people infected, after $t$ days.
If ${I_1} = 0$ (no one is infected on the first day), find ${I_t}$ up to $t = 5$.
If ${I_1} = 40$, do the same.
Write a recursive equation for
${I_t}$.
(In your formula, you may use
What happens eventually to these 2000 people?
Suppose that a less contagious cold virus infects 1/20 of the healthy population on a given day.
Find out how many days it takes for a population of 2000 to go from 0 sick people to half of the population being sick.
If you double the population to 4000, how many days do you think it will take for half of the population to get sick? Do the calculations to see if you are right.
You have 10 pet lizards and each gets fed 3 crickets at the end of every week. You buy 80 crickets, thinking that as the crickets reproduce at a rate of 50% per week, the population will sustain itself even though some crickets will be fed to the lizards. But the lizards reproduce at a rate of 10% per week. After the lizards and crickets both reproduce, then the lizards get fed.
At the end of the first week, how large is each population?
Draw a chart to track the populations over the next few weeks. Each week, round to the nearest whole number in your answers.
|
# weeks |
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|
# lizards |
10 | ||||||
|
# crickets |
80 |
Write recursive equations for ${L_t}$ and ${C_t}$, the number of lizards and the number of crickets after t weeks respectively. Your equation for ${C_t}$, the number of crickets, will have to depend on how many crickets there were last week AND how many lizards there were this week.
Do you think you’ll always have enough crickets to feed the lizards, even though the lizard population will continue to grow?
A well-fed bacteria colony in a Petri dish grows as follows:
|
# hours in dish |
1 | 2 | 3 | 4 | 5 | 6 |
|
# bacteria |
60 | 180 | 540 |
Find a pattern, and fill in the blanks.
Write a recursive equation for ${B_n}$, the number of bacteria after $n$ hours.
There are times when describing a set of data using recursive equations is the most efficient and times when it is the only thing you can do, but there are times when an explicit equation would be better. An explicit (regular) equation allows you to find any term without necessarily knowing the value of any previous term. Let’s use problem 17 as an example.
Check whether the pattern you discovered in problem 17 satisfies the equation ${B_n} = 60 * {3^{n - 1}}$. Find the size of the colony after 24 hours, by using either your recursive formula or the explicit formula.
Let the sequence $\{ {R_n}\} $ be generated by the quadratic equation ${R_n} = {n^2} + 1$.
Create a table for $\{ {R_n}\} $.
Write a recursive equation for $\{ {R_n}\} $.
Repeat problem 19 for the:
Quadratic equation,
Exponential equation ${R_n = 3^n}$.
Exponential equation ${R_n} = 3 \cdot {2^n}$.
For each chart below find a recursive equation and an explicit equation.
| n | 1 | 2 | 3 | 4 | 5 |
| ${T_n}$ | 10 | 13 | 16 | 19 | 22 |
| n | 1 | 2 | 3 | 4 | 5 |
| ${T_n}$ | 3 | 5 | 9 | 17 | 33 |
You come across the following sequence in a textbook.
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 |
| ${T_n}$ | 2 | 5 | 10 | 17 | 26 | 37 |
Find an explicit formula for ${T_n}$. (It might help to first carefully make a graph with $n$ as your horizontal axis and ${T_n}$ as your vertical axis.)
Find ${T_{100}}$.
A sequence follows this recursive rule: ${A_n} = {A_{n - 1}} - {A_{n - 2}}$.
Pick several different starting values for the sequence, and find the next ten or so values. What always happens?
How can you be sure of your conclusion in part a?
Write a recursive equation to describe the pattern you see in the Fibonacci sequence below.
| $n$ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 |
You take out a loan from a bank. At the end of each year, you pay them \$200, and then they charge 3% interest on the amount that you still owe. For example, if you borrowed \$1200, you would owe \$1,030 after 1 year.
Find out how many years it would take to pay off your loan of $1200. (Once you hit a negative number, just assume the loan is now paid off.)
In part a, did the amount of money owed decrease faster and faster as time went on, or slower and slower? Why?
Write an equation ${M_t}$ for the amount of money you owe after t years.
What happens if instead you borrow $5000? Track the loan over at least ten years.
What happens if you borrow $10,000? Track the loan over at least ten years.
Find an initial loan amount that is an equilibrium solution.
One of the simplest models for population growth is based on the idea that the growth rate of the population is proportional to the current size of the population. So, for example, we might expect that, each year, the number of frogs in a pond will increase by 6% every year.
Write a recursive equation for this model of growth.
Does this equation have any equilibria?
The population model you looked at in the previous problem has a major limitation: it doesn’t take into account the fact that the frogs in the pond have a limited number of resources (food, lily pad real estate, etc.). The following equation, called the logistic model of population growth, attempts to take this into account:
${F_{n + 1}} = {F_n} + 1.1{F_n} \cdot \left( {\frac{{40 - {F_n}}}{{40}}} \right)$
The idea here is that, the pond has a “carrying capacity” of 40 frogs — i.e., it has enough resources for 40 frogs to live healthily. So, while the population’s growth rate is proportional to the current population size, it is also proportional to how close the population is to the carrying capacity.
Suppose that there were 15 frogs in the pond. According to the equation, how much would the population change the next year? How about if there were 35 frogs in the pond?
Does it seem plausible that this system (unlike the one in the previous problem) would have an equilibrium solution other than 0?
Starting with an initial population of 2 frogs, use the equation above to track the frog population over several years. What happens in the long run?
Predict what would happen if you repeated part c, but with an initial population of 60 frogs. Then try it and see.
Exploring in Depth
Connect the midpoints of the sides of a triangle. Now connect the midpoints of the sides of your new triangle. If you could repeat this operation indefinitely it seems as though you would end up with a point. Where in the original triangle would that point be located?
Three kids sitting in a circle play a card game in which they are given a number of cards and asked on each turn to pass half of their cards to the kid sitting to their right. If they have an odd number of cards they must round up — for example, a kid who has 5 cards must pass 3. How is this game going to turn out?
Find the lowest value ever reached by the sequence $\{ {S_n}\} $, and explain why you know it’s the lowest value, given that:
${S_1} = 8000$
${S_n} = {S_{n - 1}} \cdot \frac{n}{{10}}$
A bank’s loan policy is that they calculate interest monthly: .8% per month. ${M_n}$ will represent how much money you owe the bank after $n$ months.
Suppose you start by borrowing $\$1500$ — so $M_0 = 1500$. How much do you owe after 1, 2, and 3 months?
Write a recursive equation for ${M_n}$.
If you choose to pay off the loan a little bit at a time, by paying $100 every month, calculate how much you’ll owe after 1, 2, and 3 months — assume that the \$100 is paid before interest is calculated for the month.
Write a recursive equation for ${M_n}$, under the assumptions of part c.
Now suppose the bank, hoping to make more money, decides to calculate interest every month before accepting your \$100 payment for the month. How much more will you owe at the end of 1, 2, and 3 months?
Write a recursive equation for ${M_n}$, under the assumptions of part e.
A sequence follows this recursive rule: ${F_n} = 2{F_{n - 1}}^2$.
Try starting with a few different values for ${F_1}$, and see what happens over the next 10 or so values of $n$. For which starting values do the values of the sequence increase, and for which do they decrease?
Without trying the numbers, say what will happen for the following starting values, based on what you noticed in part a — will the sequence’s values increase, decrease, or stay the same? The starting values are: 1, 1/10, ½, .99.
State and justify the “rule” you were using to make decisions in part b.
The recursive rule for a sequence $\{ {T_n}\} $ is that each term equals 30 more than the (positive) square root of the previous term.
If $T_1 = T_2$, find the number they must equal — call it $C$.
If ${T_1} > C$, what will happen to the value of ${T_n}$ as $n$ increases? How sure are you?
What if ${T_1} < C$? Are you sure?
Investigate what happens with the rule ${T_n} = \frac{{{{({T_{n - 1}})}^2}}}{n}$ when you use different starting values. You should find at least 3 different types of behavior.
For each of the sequences below an explicit equation is given. Start at $n = 1$ and figure out what happens to each sequence eventually — as $n$ gets larger and larger.
${A_n} = 1 + \frac{1}{n}$
${B_n} = {(1 + \frac{1}{n})^2}$
${C_n} = {(1 + \frac{1}{n})^3}$
${D_n} = {(1 + \frac{1}{n})^{10000}}$
Based on your answers to problem 35, what would you expect to happen to the following sequence eventually? After your guess, go ahead and check carefully on your calculator.
${E_n} = {(1 + \frac{1}{n})^n}$
You might have been a bit surprised by the answer you got for problem 36. This number happens to be quite an important number in mathematics — so important in fact that it has a special name and your calculator has a special button dedicated to it. The number is e. Check it out on your calculator.
Two animal populations are interdependent, because the predators (P) feed on the prey (Y). Here are recursive equations for the sizes of each population, in terms of time $t$ (in years):
${Y_t} = (1.03 - .001{P_{t - 1}}){Y_{t - 1}}$${P_t} = (.99 + .00002{Y_{t - 1}}){P_{t - 1}}$
If the starting population of predators is 0 and the starting population of prey is 100 (at time $t = 0$), what will happen to the prey population over time? Why does this make sense in context of the situation?
If on the other hand $Y_0 = 0$ but
If the starting populations are $Y_0 = 450$ and $P_0 = 45$, track what happens in the first ten years.
What should the starting populations be, for both populations to remain stable? Use what you saw in part c, or look at the equations themselves to figure it out.
You invest in a stock through a broker. ${M_t}$ is how much money you have after $t$ years. Every year, the value of your stock increases by 9%, but your stockbroker also charges a fee at the end of each year — $\$100$ the 1st year, $\$200$ the 2nd year, $\$300$ the third year, and so on.
If you invest $\$3000$ initially, how much money do you have each year over the next five years? What’s the trend?
Write a recursive equation for $\{ {M_t}\} $.
How much money would you have to start with, so that after 1 year you have exactly the same amount of money?
If you invested more at the beginning, would your money always grow, or would it still eventually decrease?
Don’t use a calculator for this problem.
Solve for $x$: ${x^2} - 6x = - 2$
Simplify $\frac{\sqrt{6} \sqrt{15}}{\sqrt{10}}$
Simplify ${\left( {\frac{{2{x^2}{y^{ - 3}}}}{{3{x^{ - 1}}{y^4}}}} \right)^{ - 2}}$
Add $\frac{x}{5} + \frac{4}{x}$
Simplify $\frac{{\sqrt {48} }}{8}$