Introduction
Last year, you discovered that whenever you inscribed a triangle in a circle with one side being a diameter of the circle, the triangle seemed to be a right triangle. And some of you might have concluded, not without good reason, that this must always be the case. This kind of reasoning is called $inductive reasoning$— when you use a set of examples to claim a general theory.
Most of you, however, may have remained unconvinced that this would be always the case, and set out to prove it using some of the axioms of geometry. The kind of reasoning you used is called $deductive reasoning$— the kind of reasoning preferred by mathematicians, and the kind which will be the focus of this lesson.
In mathematics, inductive reasoning is often used to make a guess at a property by examining some cases, and deductive reasoning (deduction) to prove that the property generally holds.
As in the case of the circle example above the conclusion reached by inductive reasoning proved to be indeed correct, but in many cases, conclusions reached by inductive reasoning will turn out to be false. If you check the value of the expression for the first 10 or so positive integer values of $n$, you might conclude that was a prime number for any positive integer $n$. It turns out that this is not the case.
Can you find a value for n such that the expression is not a prime number?
Which of the following do you think might be an example of deductive reasoning? Inductive reasoning? “Reasoning” that is neither inductive nor deductive? Explain.
All dogs are friendly. All friendly things are huggable. If something is huggable then it’s a cat. Therefore, all dogs are cats.
All dogs are blue. All animals are blue. Therefore, all dogs are animals.
Every year since records were kept, if it rained in Cyber City on a particular day, it has rained three days later. It rained in Cyber City this past Monday. Therefore, it will rain in Cyber City this Thursday.
Whenever the weather is fine, Rose goes to the beach. Rose is now at the beach. So the weather must be fine.
In this lesson not only will we explore logic problems including some similar to the ones in problem 1, but we will also introduce a different kind of geometry, called $finite geometry$. As its name suggests, finite geometry, unlike the geometry to which you are accustomed with an infinity of points, lines, planes, and so on, concerns itself solely with finite numbers of elements.
We will study some of these geometries not only because of their quirky elegance but also because they provide a look into the nature of mathematical proof and help to sharpen your skills in developing valid logical arguments. They also show the power of visualization as an aid in solving more difficult problems.
Development
As you know from your work in Euclidean Geometry, any system of deductive reasoning consists of undefined terms, definitions, postulates (axioms), rules of logic (akin to common sense), and theorems (proved statements).
Recall that a $postulate$($axiom)$ is a statement whose truth is to be accepted without proof, such as the line postulate in Euclidean Geometry, which states that one and only one line can be drawn through 2 distinct (different) points.
And the truth of a $theorem$ is established by applying the rules of logic to the postulates. At each step in the proof of a theorem you must indicate which postulate you are applying, or which previously proved theorem you are drawing upon.
Why must there be undefined terms? Is it possible to define every word/term? Try defining the color blue for a person who has no idea what blue is. And assume that if a person does not know what blue is, it is likely that the person will not know a host of other words associated with the color blue.
But, of more importance, would the correctness of your reasoning be in question if some of the words used in the postulates were not defined? For example, supposed we replaced some of the words in problem 1a with words whose meanings you did not know, would you still conclude that it was a case of deductive reasoning?
Is the following an example of deductive reasoning? Inductive reasoning? “Reasoning” that is neither inductive nor deductive?
All blewters are sartoasted. All sartoasted things are ducated. If something is ducated then it’s an ook. Therefore, all blewters are ooks.
Let’s try to draw a conclusion using all of the three postulates below.
Postulate 1. No ooks are acks. Postulate 2. All kooks are ooks. Postulate 3. All pocks are acks.
Draw, if possible, a diagram satisfying all three postulates using exactly 3 ooks, 2 kooks and 4 acks.
Compare your answer to part a with others. How many ooks did you have that were not kooks? How many acks did you have that were not pocks?
In problem 3, is it correct to conclude that no kooks are pocks? Prove your answer.
There are a few different ways to solve problem 4. You might have used a kind of indirect argument, or, if you are more visually inclined, you might have used a Venn diagram, as suggested by problem 3.
Let’s first look at an indirect argument.
We’re eventually trying to prove that no kooks are pocks, but to start out, suppose that the opposite were true. That is, suppose there is some kook that is also a pock. Using Postulate 3, what conclusion can you draw about that kook?
Using your answer to part a, and Postulate 1, what new conclusion can you draw about our kook?
Now use Postulate 2 to complete your argument.
This kind of argument you used in problem 5 is called $proof by contradiction.$ Here is how it works. First, assume that the original statement you want to prove is false. Second, by reasoning from this assumption, reach a conclusion that is impossible — impossible, either because it contradicts a postulate or an established theorem, or because it contradicts the given information. Third, since assuming your original statement was false led to contradictions of known facts, you can now conclude that the original statement must instead be true.
This kind of argument, proof by contradiction, makes use of a very important fact in the rules of logic — that any statement is equivalent to (exactly the same as) its $contrapositive$. Some of you may have encountered this term before. Here’s an example of a statement and its contrapositive.
Statement: To be selected for Eightnotes you have to be a singing sensation.
Contrapositive: If you are not a singing sensation, then you will not be selected to Eightnotes. [or you can kiss Eightnotes goodbye.]
Here’s another:
Statement: If an animal is a zebra, then it has stripes.
Contrapositive: If an animal does not have stripes, then it is not a zebra.
Would you agree that in the example above the statement and its contrapositive are equivalent? What follows is a somewhat less subtle use of the contrapositive. In the problem, x is considered to be an integer.
If x is not equal to 3, then ${x^3}$ is not equal to 27.
Write the contrapositive of the above statement.
Is it easier to prove the statement directly, or to prove its contrapositive?
Back to problem 4. For a more visual approach, you might have represented each postulate by a Venn diagram (see below) and used the final picture to reach your conclusion.
 $Postulate 1
$
$Postulate 1
$ $Postulate 2$
$Postulate 2$ $Postulate 3$
$Postulate 3$Draw Venn diagrams for the postulates in problems 1a and 1b, and use them to check the answers you gave earlier.
Next we will take a look at some finite geometries. But before we explore a more traditional example with “points”, “lines”, etc., let’s look at one that might be a tad more familiar.
Postulate 1. There are six people and four entrees. Postulate 2. Everyone is sharing at least one entree with at least one other person. Postulate 3. Everyone is eating.
Draw out two different actual dinners that satisfy the postulates. In your diagrams you may use anything you please to represent people and entrees, but you have no choice regarding six and four.
The diagrams you drew are called $models$.
Here is a more traditional one with three postulates. The terms “lines” and “points” are undefined and you must resist the temptation to think of these elements the way you did in Euclidean Geometry. For example, in a finite geometry a “line” cannot contain an infinite number of “points” since there are only a finite number of “points” in these geometries.
Postulate 1. There are 5 points and 5 lines. Postulate 2. Every line contains at least 2 points. Postulate 3. Every point is on at least one line.
Check that the following diagram represents the set of postulates — that, in fact, it is a model.

The following is also a model for the system, but is essentially the same as the one above. Why does this claim make sense? (Think back to your graph theory lesson.)

On a soccer team, 5 students are vying for 5 spots. The coach wants to make sure that there are at least 2 players for each position, and that each player gets to play in at least one position. Draw a model for this system.
Using the postulates and models of problem 9, one group of students concluded that every point must be on at most two lines. Draw a model different from those in problem 7 to refute that claim.
Although models are extremely helpful in creating and examining conjectures, you have to be careful not to rely on models to construct proofs. In a very few cases it might be possible to construct every possible model satisfying all the postulates, but in general that would be very difficult to do. And even if you could construct all possible models, it might still be difficult to prove that you have done so. So to prove conclusions, you should reason directly from the postulates.
Based on your models in problems 9 and 11, make a claim, then try to refute it by drawing yet another model satisfying all the postulates of problem 9.
In the following geometry with four postulates, lines and points are undefined.
Postulate 1. There exist exactly 3 points. Postulate 2. Given any 2 points, there is exactly one line on them. Postulate 3. Not all points are on the same line. Postulate 4. Given any 2 lines, they are on at least one common point.
Draw a model.
Prove that 2 different lines cannot have more than one point in common. (You may use postulate 2 and proof by contradiction.)
Can there be 4 lines?
Prove that not all lines have the same point in common.
Are there parallel lines in this system? (In finite geometries, two lines are $parallel$ if they do not share a common point.)
Before working in any deductive system it is important to examine the postulates for $consistency$— is it possible for all the postulates to be true at the same time? The rule of thumb is that if you can draw a diagram to represent the set of postulates, then the postulates are consistent. Can you come up with some reasonable argument why drawing a diagram would allow the claim that the postulates are consistent? The systems in problems 8 and 9 passed the test since we were able to construct a model for each.
Check the following system for consistency. Lines and points are undefined terms.
Postulate 1. There are 4 points and 5 lines. Postulate 2. Every line contains exactly 2 points. Postulate 3. Every point is on exactly 2 lines.
Let’s now create a finite geometry that seems less abstract than the previous two.
Replace undefined terms “points” and “lines” in problem 13 by new undefined terms “students” and “committees” respectively, and rewrite the four postulates, changing the language a bit to make sense with the new terms.
Draw a chart of students and committees that would represent the postulates. (Your chart should have 3 rows for the 3 students, and as many columns for committees as you wish.)
Are your postulates in part a consistent?
How many committees did you finally end up with?
Is there a student who is on all committees?
Practice
Which of the following do you think might be an example of deductive reasoning? Explain.
Any student not voting is irresponsible. Jumbo did not vote. Therefore, Jumbo is irresponsible.
Any student not voting is irresponsible. Jumbo is irresponsible. Therefore, Jumbo did not vote.
If bruins win, then cardinals weep. If students don’t turn in their papers, then teachers become depressed. If students turn in their papers, then cardinals don’t weep. Therefore, if bruins win, teachers become depressed.
Write the contrapositives for the following statements.
If two angles are right angles, then the two angles are congruent.
If you are a Park student, then you will seek the truth.
If it doesn’t rain, I’ll go to the park.
All apples are red.
Describe a geometry with postulates the same as in problem 13 except, instead of points and lines use birds and trees, beads and wires, trees and rows of trees, stars and galaxies, or some other pair of your choice.
For the following geometry with three postulates, the undefined terms are “points” and “lines”.
Postulate 1. There are 3 points. Postulate 2. Every line contains exactly 2 points. Postulate 3. Every point is on at least one line.
Draw two different models.
Could there be any parallel lines in this geometry?
In problem 19 above, it seems as though there can be no more than 3 lines. What do you think?
Problems
Write a concluding statement for the following. If one is not a croot, then one is not a lurl. If one is a bleep, then one is a gurm. If one is a pift, then one is a lurl. If one is a croot, then one is not a gurm.
Therefore, if . . . . . . . then . . . . . . .
(Make sure your conclusion makes use of all of the postulates.)
What conclusion can you draw from the following?
If the triangle is acute, then the problem will be easy. If you are in Tony’s class, then the problem will not be easy. If the triangle is acute, then you are in Tony’s class.
Back to problem 13.
Prove that there exist 3 and only 3 lines. (You may use the theorem you proved in part b as well as postulates 4 and 1, and proof by contradiction.)
Try to draw a model that is different from your model in part a of problem 13.
Determine the consistency of each of the following systems.
In this system, the following 3 axioms hold. Squirrels and trees are the undefined terms. Postulate 1. There are exactly 3 squirrels. Postulate 2. Every squirrel climbs at least 2 trees. Postulate 3. No tree is climbed by more than 2 squirrels.
In this system, the following 4 axioms hold. Hearts, spades and trump(s) are the undefined terms. Postulate 1. There is at least one heart. Postulate 2. For each pair of spades, there is one and only one heart that trumps them. Postulate 3. Each heart trumps at least 2 spades. Postulate 4. Given any heart, there is at least one spade it does not trump.
In this system, the following 5 postulates hold. Lines and points are the undefined terms.
Postulate 1. Each pair of lines has at least one point in common. Postulate 2. Each pair of lines has no more than one point in common. Postulate 3. Every point is on at least 2 lines. Postulate 4. Every point is not on more than 2 lines. Postulate 5. There exist exactly 4 lines.
Is the system consistent?
Prove that every pair of lines has exactly one point in common.
Prove that every point belongs to exactly 2 lines.
Prove that there are exactly 6 points.
Prove that every line contains exactly 3 points.
Are there parallel lines in this system?
Here’s a chance for you to create your own geometry.
Invent an axiom system and a model for it.
Prove a theorem in your geometry.
Now add an additional axiom that would make the system inconsistent.
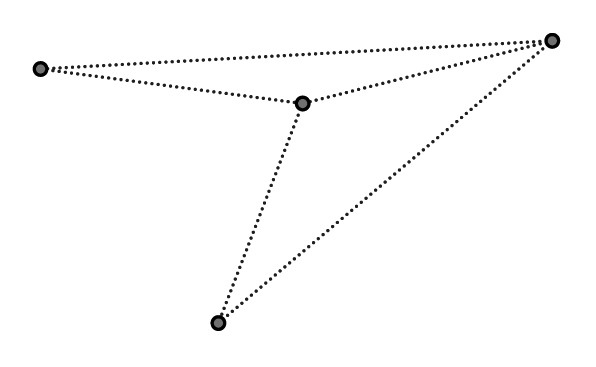
Use postulates to describe a geometry that would fit the model below.
In the following three problems, make sure that your solution constitutes a good argument.
Three large containers are filled with marbles. One is filled with red marbles, one with blue, and one with a mixture of blue and red marbles. The problem is that the containers have all been mislabeled, plus none of the containers has the correct label. Describe how you would correctly label the containers looking at the least number of marbles.
And how about this quite famous one. Someone is looking at a picture and says: “Brothers and sisters have I none, but this man’s father is my father’s son.” Who is in the picture?
In this system, the following 6 postulates hold. Lines and points are the undefined terms.
Postulate 1. Given any two points, there is at least one line that contains them. Postulate 2. Given any two points, there is at most one line that contains them. Postulate 3. Given any two lines, there is at least one point that is contained in both lines. Postulate 4. Given any line, there are at least three points that are contained in the line. Postulate 5. Given any line, there is at least one point that is not on the line. Postulate 6. There is at least one line.
Are there parallel lines in this system?
Prove that there exists at least one point.
Prove that any 2 points are on exactly one line.
Prove that 2 lines have exactly one point in common.
Prove that if P is any point, there is at least one line that does not contain P.
Prove that every point lies on at least 3 lines.
As we did in problem 15, let’s make problem 30 a little less abstract.
Replace undefined terms “points” and “lines” by new undefined terms (you use “students” and “committees” again if you like), and rewrite the postulates, changing the language a bit to accommodate the new terms.
Draw a chart that would represent the postulates. How many “points” did you end up with? How many “lines”?
Would the addition of another “point” or “line” violate any of the postulates?
Is the following diagram a model for the system in problem 30? If you think not, explain.
Decide whether or not the following system is consistent:
Postulate 1. The town of Fairhaven consists exclusively of married couples and their children. Postulate 2. There are more adults than children. Postulate 3. Every boy has a sister. Postulate 4. There are more boys than girls. Postulate 5. There are no childless couples.
A system is considered $dependent$ if at least one of the axioms follows from the other axioms; otherwise it is considered $independent$. To show that a system is dependent, it is only necessary to show that one axiom follows from the others. However to show that a system is independent, one must show that no one axiom follows from the others.
Construct two systems, one independent and one dependent.
Don’t use a calculator for this problem.
Add $3x + \frac{1}{{2x}}$
Subtract $\frac{{16}}{x} - \frac{{4 + x}}{{{x^2}}}$
Simplify $\sqrt {75} - \sqrt {24} + \sqrt {18} $ z
Solve ${x^2} + 3x = 2$
Exploring in Depth
