Introduction
In an earlier lesson, you learned how the trigonometric functions sine, cosine, and tangent were defined for angles other than those between 0 and 90 degrees. Here is a quick refresher.
Imagine sitting at the edge of a merry-go-round with radius 1 meter. You’ve set up a coordinate system with (0,0) at the center of the merry-go-round, and the point (1,0) is due east from (0,0). When the wheel starts to turn counterclockwise, your position is (1,0).
If the merry-go-round has rotated $42^\circ$ from its starting position, find the coordinates of your position.

If the merry-go-round has rotated $200^\circ$ from its starting position, find the coordinates of your position.
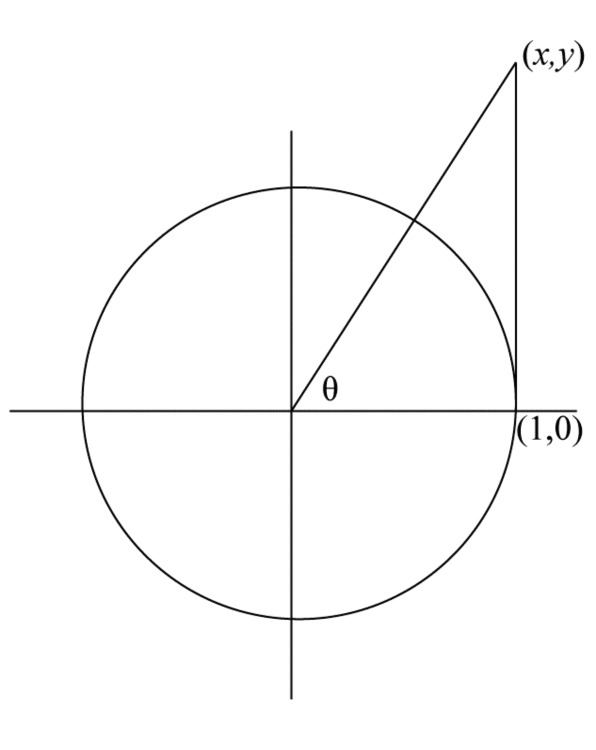
This may be enough to remind you of the generalized definitions of sine and cosine. In the figure below, a “spoke” of a circle of radius 1 is drawn so that it makes a central angle of $\theta $ with the positive $x$-axis. The spoke intercepts the circle at the point $(x,y)$. The sine of an angle $\theta $ is the $y$-coordinate of this point. The cosine of $\theta $ is the $x$-coordinate of this point.
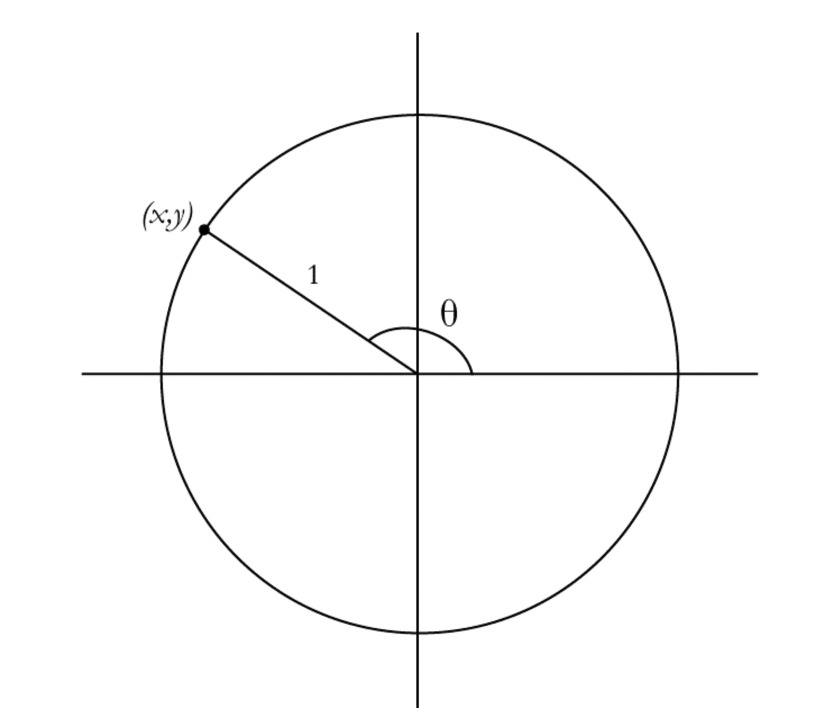
Using the figure above, how would you define the tangent of $\theta $?
In middle school, you learned that $\sin \theta $ is defined as $\frac{\text{length of the side opposite } \theta \text{ in a right triangle}}{\text{length of the hypotenuse}}$. Where is the right triangle in the figure above, and what are the opposite and hypotenuse?
How would you determine the sine, cosine, and tangent of an angle using a circle with a different radius than 1?
The circle with radius one is better known in mathematical circles as the “unit circle.” You’ll want to draw it — or a circle with a well-chosen radius — almost every time you solve a trig problem.
Development
Cecilia is on a Ferris wheel and notices that, when she has rotated about 143 degrees from due east, she is 24 meters west and 18 meters above the center of the wheel. Use this information to approximate the sine, cosine, and tangent of 143 degrees. Then see how you did by asking your calculator for these values.
For each diagram, find the sine and cosine of the angle $\theta $.



Copy the following 30-60-90 triangle and 45-45-90 triangle into your notebook. Then write in the remaining angles and find the remaining sides in terms of $x$.

Problem 2 may have reminded you that whether the sine or cosine of an angle is positive or negative depends on which quadrant the angle is in. This allows you to answer questions like the following.
Go back to your 30-60-90 and 45-45-90 triangles and think about positioning them on the unit circle.
Name all angles between 0 and 360 degrees that have a sine of $\frac{1}{2}$.
Name all angles between 0 and 360 degrees that have a cosine of $\frac{1}{2}$.
Name all angles between 0 and 360 degrees that have a tangent of 1.
Now explain how to find all the angles that have a sine of $\frac{1}{2}$.
Solve the equation $\sin \theta = \frac{1}{2}$. How many solutions are there? How many solutions are interestingly different from one another?
Of course, you might also have to solve equations that don’t involve sines or cosines of angles in special triangles. For instance, if you had to solve $\sin \theta = .2531,$ you would be forced to resort to the inverse sine function on your calculator.
Make sure your calculator is in degree mode, then take the inverse sine of .2531 to solve this equation.
Draw the “wheel” again, and draw a spoke at the angle that has sine .2531. Remembering that the sine of an angle is the height of a point above the $x$-axis, indicate the other point on the wheel that would have the same sine.
How would you calculate the size of this second angle with sine .2531? Do so.
Give all the solutions to the equation $\sin \theta = .2531$.
Now find all the solutions to the equation $\cos \theta = .2531$.
Practice
A wheel of radius 2 ft spins around the point $(0,0)$. A ladybug sticker is initially at the point $(2,0)$. Find the coordinates of the sticker once the wheel has spun
$115^\circ$
$220^\circ$
$300^\circ$
$660^\circ$
Calculate the exact value of each expression. Do not use a calculator.
$\sin 120^\circ $
$\cos ( - 60^\circ )$
$\cos 315^\circ $
$\tan 150^\circ $
$\sin 270^\circ $
$\cos 0^\circ $
Given that the sine of 138 degrees is about .6691,
Find all angles between 0 and 360 degrees that have a sine of .6691.
Describe all angles that have a sine of .6691, including those not between 0 and 360 degrees. Can you find a way to write your answer using symbols?
Find all solutions to the equation $\sin \theta = .6691$.
Find all solutions to the equation $3\sin \theta - 1 = 1.0074$.
Find all solutions between $0^\circ$ and $360^\circ$ to the equation $\tan \theta = \dfrac{{ - 1}}{{\sqrt 3 }}$.
Find all solutions between $0^\circ$ and $360^\circ$ to the equation $\cos \theta = - .8834$.
In which quadrants is the tangent negative? In which quadrants is the tangent positive?
Further Development
You’re used to measuring temperature in degrees Fahrenheit, but you also know that much of the world measures temperature using degrees Celsius. Similarly, the world uses miles and kilometers, ounces and grams, gallons and liters.
When the Babylonians invented degree measure, they chose a 360-degree circle for two reasons. One was that, since there are 365 days in a year, a degree would be very close to one day’s progress around the circular path they believed the sun made every year. Another reason is that 360 is divisible by lots of numbers, so we can describe a fourth, a sixth, an eighth, and a tenth of a circle as an integer number of degrees. (Try this with a 100 degree circle and you’ll see it doesn’t work as well.)
As time went on, though, mathematicians realized that the number 360 didn’t really have anything to do with circles, and in fact some of their calculations would be easier if they used a different system. This system was inspired by the close relationship between a central angle of a circle and the arc it intercepts. It was also inspired by the importance of the unit circle.

Specifically, we’d like the measure of a central angle in the unit circle to be literally the same as the length of the arc it intercepts.
What is the circumference of the unit circle?
Since a 360 degree “central angle” intercepts the entire circle your answer to Problem 24 will be the equivalent of 360 degrees in our new system.
How much of a circle does a 180 degree central angle intercept? So, in this new system, how should we represent a 180 degree angle?
Under this new system, what should we call the measure of an angle that intercepts a quarter-circle?
What should we call the measure of an angle that intercepts a sixth of a circle?
When you measure angles this way, you are measuring in radians. (Try pressing the MODE button on your calculator and notice that there is a radian vs. degree option.) The next problems suggest a reason for the name.
How many times does the radius of a circle “fit” around the circumference? (Hint: remember that the circumference of a circle is $C = 2\pi r$.)
Say you have an angle that intercepts an arc on the unit circle equal to two of its radii. How many radians is that angle?
If you are about to solve an equation like $\sin \theta = \dfrac {\sqrt {3}} {2}$, you might not know whether to give your answer in degrees or radians. Your class should agree on which system to use.
Practice
If 60 degrees is equivalent to $\dfrac{\pi }{3}$ radians, how many radians are in
120 degrees?
240 degrees?
30 degrees?
15 degrees?
Use your answers to the previous problem to help convert each degree measure to radians.
75 degrees
150 degrees
330 degrees
If 45 degrees is equivalent to $\dfrac{\pi }{4}$ radians, how many degrees are in
$\dfrac{{3\pi }}{4}$ radians?
$\dfrac{{7\pi }}{4}$ radians?
$\pi $ radians?
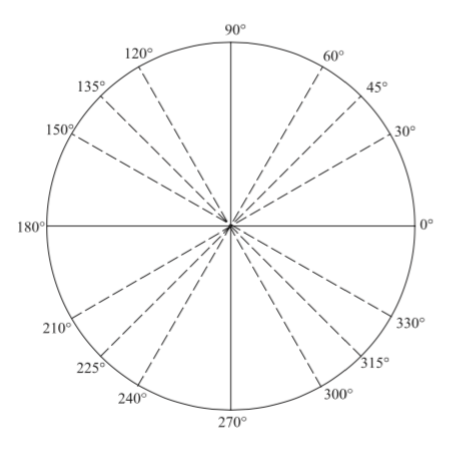
Copy this unit circle into your notebook and write the radian measure of each angle marked.
Give the exact value of each expression.
$\sin \dfrac {\pi} {3}$
$\cos \dfrac {\pi} {3}$
$\sin \dfrac {2\pi} {3}$
$\cos \dfrac {2\pi} {3}$
$\tan \dfrac {7\pi} {4}$
$\cos \dfrac {5\pi} {4}$
Problems
Write each set of values in order of smallest to biggest. Do not use a calculator.
$\sin {60^ \circ }$, $\sin {70^ \circ }$, $\sin {80^ \circ }$
$\cos {60^ \circ }$, $\cos {70^ \circ }$, $\cos {80^ \circ }$
$\tan {60^ \circ }$, $\tan {70^ \circ }$, $\tan {80^ \circ }$
Write each set of values in order of magnitude (that is, you would write 2 before –10) and then say which are positive and which are negative.
$\sin {89^ \circ }$, $\cos {89^ \circ }$, $\tan {89^ \circ }$
$\sin {269^ \circ }$, $\cos {269^ \circ }$, $\tan {269^ \circ }$
$\sin {359^ \circ }$, $\cos {359^ \circ }$, $\tan {359^ \circ }$
Solve each equation for all values of $\theta $. You may use your calculator, but keep in mind that it will not give you all the answers you need.
$\cos \theta = .4642$
$\dfrac {1} {3} \sin \theta = .2862$
$2\tan \theta - 4 = - 3.5174$
$\sin \left ( \theta - 15^\circ \right ) = .7327$
Solve for all values of $x$. Give answers to Part a using degrees and answers to Part b using radians.
$\sqrt 2 \sin \left( {x + {{45}^ \circ }} \right) = 1$
$\sqrt 3 \tan \left( {x + 4} \right) = 3$
Solve for all values of $\theta $.
${\tan ^2}\theta = 3$
$\left( {\sqrt 3 \sin \theta + 1} \right)\left( {2\sin \theta - 1} \right) = 0$
Does ${\sin ^{ - 1}}x$ refer to an angle, or just a number that does not represent an angle? How about $\sin x$?
A wheel on a buggy has a radius of one foot. How many degrees has it spun counterclockwise if a chalk mark originally on the wheel’s rightmost point is for the first time .8 feet off the ground?
Don’t use a calculator for this problem.
Solve: $x^4 - 9x^2 = 0$
Solve: $\dfrac{3}{{27}}{x^2} = 1$
Find the base-ten logs of a million, a billion, and a million times a billion.
Solve: $\dfrac {x+1} {x+3} = 14$
Simplify: $\dfrac{{{{\left( {{x^2}} \right)}^6}}}{{{x^3}}}$
A Ferris wheel has a radius of 132 feet. Its bottom seat is 6 feet off the ground. You are sitting in the seat at the wheel’s rightmost point when the wheel begins to spin counterclockwise.
What is your height off the ground when the Ferris wheel has rotated $\dfrac {5\pi} {4}$ radians?
What is your height off the ground when the Ferris wheel has rotated $\dfrac {9\pi} {4}$ radians?
What is your height off the ground when the Ferris wheel has rotated $\dfrac {13\pi} {4}$ radians?
You have fallen asleep on the Ferris wheel. When you wake up, you realize that you are level with a tower that you know to be 100 feet off the ground. What are the possibilities for how many radians the wheel has rotated since the beginning of the ride?
How many degrees is one radian? How many radians is one degree?
Come up with a conversion formula between degrees and radians.
Another way of thinking of radian measure is as a ratio. In a circle, it is the ratio of the arc an angle intercepts to the radius of the circle.
Draw a circle of radius 5 inches, with an angle inside that intercepts an arc that is $\frac{1}{4}$ the length of the circle. Find the ratio of the arc length to the radius.
Repeat part a, but using a circle of radius 7 inches. Your angle will still intercept $\frac{1}{4}$ of the circle.
What is the radian measure of an angle that intercepts a quarter-circle?
In 10th grade, you found a formula for the length of an arc intercepted by an angle $\theta $: arclength $= 2\pi r \cdot \dfrac {\theta} {360^\circ}$. Find a similar formula that works when the central angle is measured in radians instead of degrees.
In 10th grade, you also found a formula for the area of the sector the angle intercepts: sector area $= \pi r^2 \cdot \dfrac {\theta} {360^\circ}$. Find a similar formula that works when the central angle is measured in radians instead of degrees.
From what we’ve seen in this lesson, there are often two solutions to the equation $\cos \theta = A$ between $0^\circ$ and $360^\circ$.
Are there any values of $A$ for which there would only be one solution? How many values of $A$?
Are there any values of $A$ for which there would be no solutions?
Suppose an angle has a sine of .4221.
How many angles have this sine?
Your calculator tells you that ${\sin ^{ - 1}}\left( {.4221} \right) \approx {24.97^ \circ }$. Why do you suppose it only gives you one answer?
Try to figure out how the calculator “chooses” the answers it gives for the inverse sine button. What’s the biggest answer it will give? What’s the smallest?
Repeat part c of the previous problem for inverse cosine and inverse tangent. Why do you suppose the range of answers is not the same for the sine and cosine?
If $2\theta = {26^ \circ } + {360^ \circ }n$, where $n$ stands for any integer,
Find all possible values for $\theta $.
Did your possible values include $\theta = 553^\circ$? If not, revise your answer to part a.
If $3\theta = {150^ \circ } + {360^ \circ }n$, where $n$ stands for any integer, find all possible values of $\theta $.
Solve each equation.
$\sin 2\theta = .1647$
$\tan 2\theta + 5 = 42$
$2\sin 3\theta = \sqrt 3 $ (no calculator)
$\cos 3\theta = \dfrac{1}{{\sqrt 2 }}$ (no calculator)
Exploring in Depth
Find the coordinates of the point labeled $\left( {x,y} \right)$ in terms of $\theta $. Does the diagram suggest a certain word origin?
How many solutions does $\sin n\theta = \dfrac{{\sqrt 3 }}{2}$ have between $0^\circ$ and $360^\circ$? Answer in terms of $n$.
Refer back to Problem 46, in which you thought of the radian measure of an angle as a ratio. Explain why, unlike degrees, miles, or kilograms, radian measure doesn’t require units.