Introduction
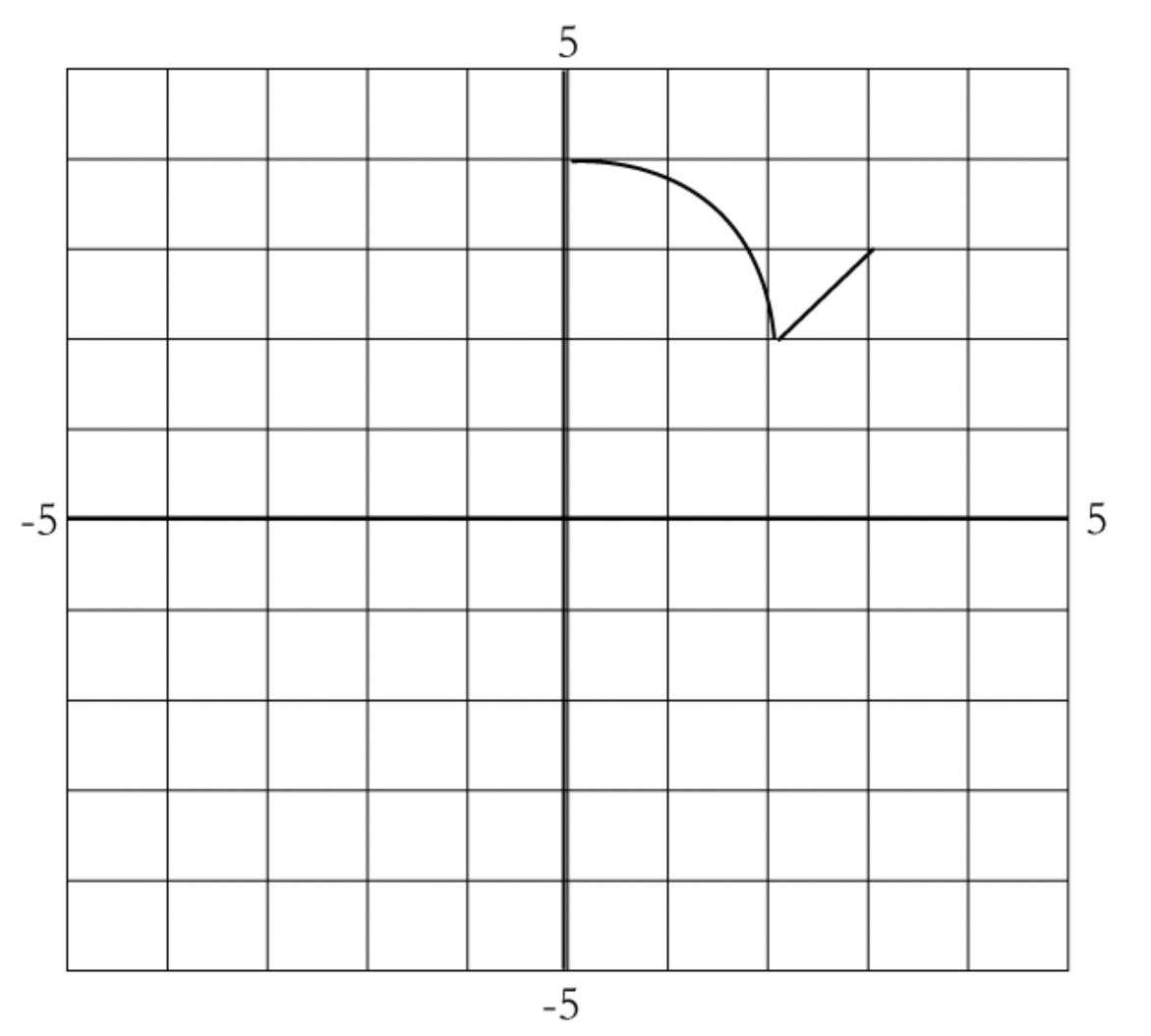
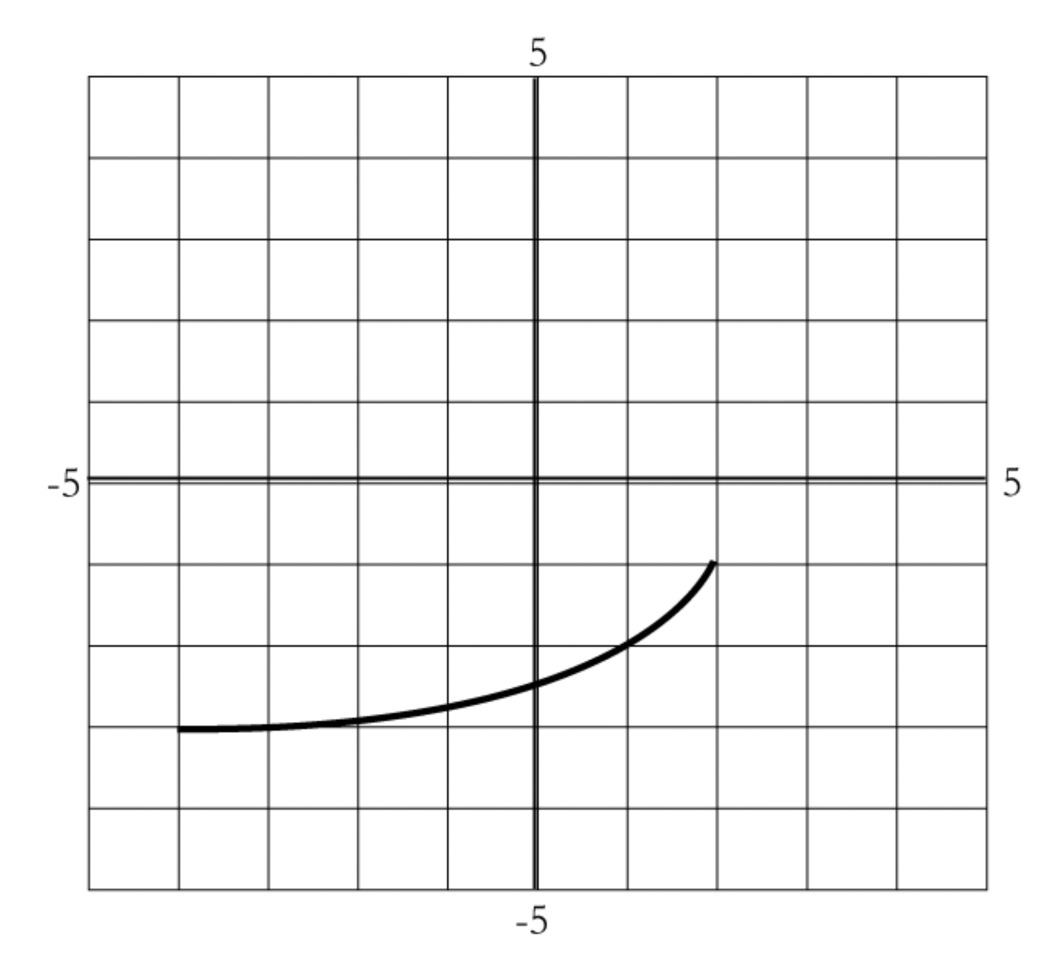
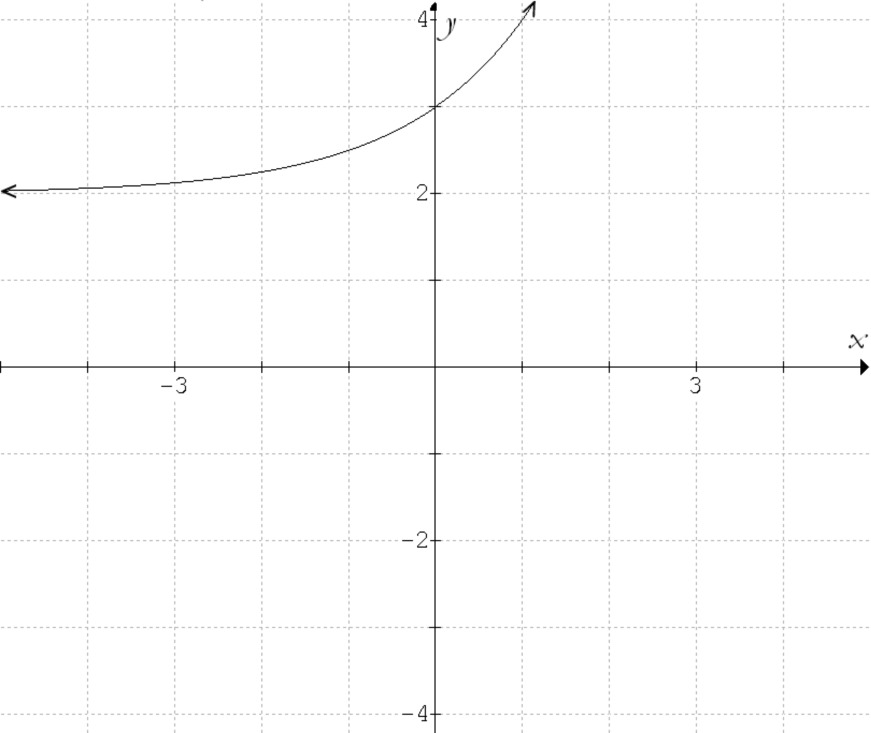
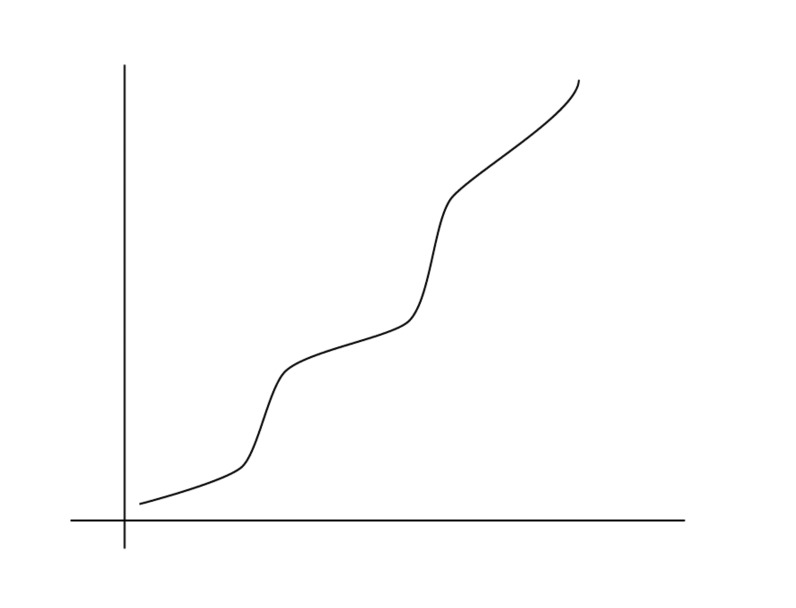
In previous lessons, you may have used exponential, logarithmic, and power functions to model data. For instance, if you had evidence that the data could be modeled by an exponential function, then your task was to find values for $a$ and $b$ in the function type $f(x) = a{b^x}$. However, one problem in the Exponential Functions lesson involved a kind of exponential function for which it wouldn’t work simply to find $a$ and $b$. A 180$^\circ$ cup of coffee is left out to cool in a 70$^\circ$ room. Below is a graph showing the temperature of the coffee over time.

A function that does a decent job of modeling this data is $f(x) = 99.5{(.895)^x} + 71.$ You can think of the function as a translation of 71 units up of the more familiar function $g(x) = 99.5{(.895)^x}$.
It’s easy to imagine changing the vertical shift of $g$ in order to produce lots of different functions, perhaps corresponding to cooling curves in rooms of different temperatures. More generally, in modeling data it’s useful to be able to start with basic function types and use transformations in order to control the shape and position of those graphs. We will begin our study of this technique by examining more abstract types of functions.
Development
Below is a graph of a function $f$. Note that $f$ is not one of the function types you have studied before. It does not have a nice formula. But its graph is still enough for you to answer questions about input and output.
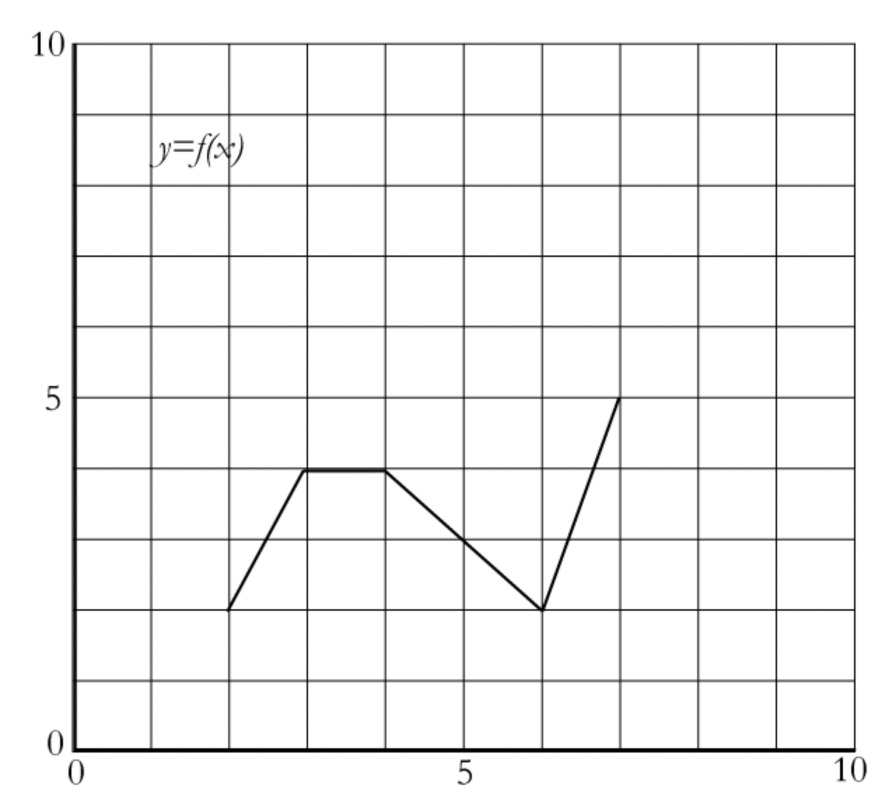
A table of values for the function might look like this:
|
$x$ |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
$f(x)$ |
--- | 2 | 5 | --- |
Fill in the four missing values.
Note that we say “a table of values” “might” look like this because there are far more points on the graph of this function. If you wanted to, you could use $x = 3.5$ in the table, or even $x = \pi $. The dashes in the table are there because the function is not defined for certain inputs: specifically, for $x < 2$ and $x > 7$. Another way of saying this is that the domain of the function is $2 \le x \le 7$.
Using the same function f as in problem 1, draw the following graphs. If you need help getting started, remember that an expression like “$f(4) + 2$ ” means “two more than the value of $f(4)$.”
$y = f(x) + 2$
$y = \frac{1}{2}f(x)$
$y = - f(x)$
In Problem 2, you saw examples of a vertical translation, a vertical contraction, and a reflection over the $x$-axis. Horizontal transformations merit a little more attention.
Much as we can define the function $y = f(x) + 2$, we can define the function $y = f(x - 2)$.
Find the output of the function $y = f(x - 2)$ for the input $x = 5$.
Make a table of values with the headings $x$ and $y = f(x - 2)$, and fill it in. Take care to think about which values of $x$ it makes sense to use.
Using the values from your table in Problem 3, graph the function $y = f(x - 2)$. How was the graph of $y = f(x)$ transformed to make this new graph?
What is the domain of the function you graphed in Problem 4?
Conjecture a formula (like $y = f(x - 2)$ ) that translates the graph of $y = f(x)$ three units to the left. Then make a table and/or graph to see if you are right.
Now consider the function $y = f(2x)$. First find the output when $x = 2$. Then make a table of values with the headings $x$ and $f(2x)$, and fill it in. Take care to think about which values of $x$ it makes sense to use.
Using the values in your table from Problem 7, graph the function $y = f(2x)$. Describe the transformation of the graph of $y = f(x)$ this represents.
What is the domain of the function you graphed in Problem 8?
Conjecture a formula that horizontally stretches the graph of $y = f(x)$ so that each point is three times farther away from the y-axis.
Use a similar process to graph $y = f(-x)$ . What transformation of the graph of $y = f(x)$ does this represent?
Find a formula for $f( - x)$ if $f(x) = {x^2} + 2x - 8$. Then sketch the graphs of $y = f(x)$ and $y = f( - x)$ on the same axes.
Using transformations is one way to build a new function from a known function. You can also combine two functions to get a third.
Let $f$ be the function from the introduction (shown below, on the left), and $g$ be the function defined by the graph below, on the right.
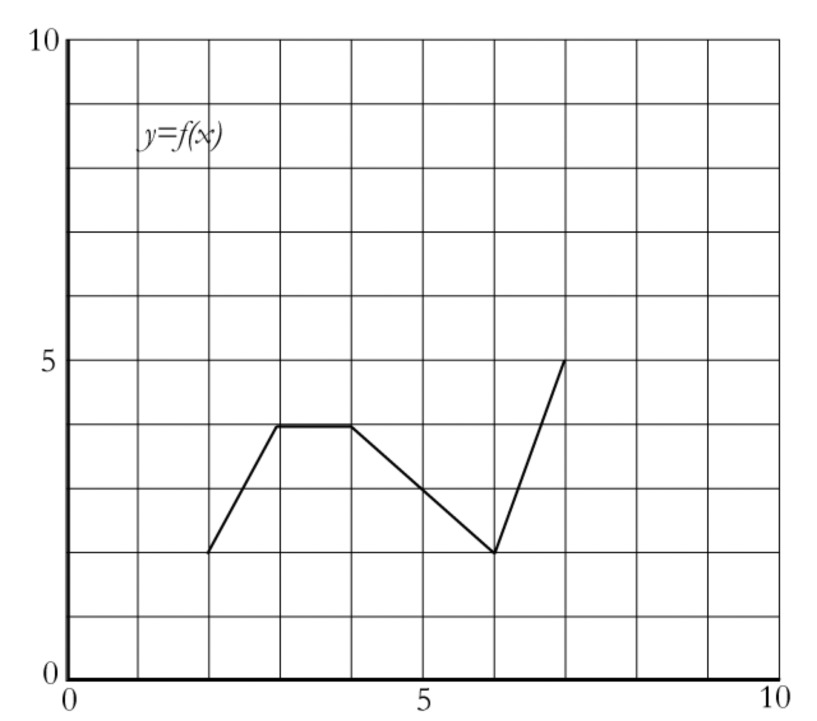

The function $h$ is defined by the equation $h(x) = f(x) + g(x)$. For example, to find the value of $h(3)$, you would add together the values of $f(3)$ and $g(3)$. Find $h(3)$, then sketch a graph of $h$.
Now sketch a graph of $j(x) = f(x) - g(x)$.
The following exercise illustrates another way to combine functions, known as composition of functions. Composition is when you “chain” two functions together, by taking the output of one function and using it as the input to a second function. To see why this might be useful, consider the following situation.
Howie is chewing Super-Bubble gum and blows a super-bubble. The radius (in inches) of his bubble increases with time (in milliseconds) in a way given by the equation $r(t) = 2t^{0.25}$. What is the volume of Howie’s bubble 5 milliseconds after he blows it?
In order to solve the previous problem, you had to do two things. First, you had to find the radius of the bubble at 5 milliseconds. Then you had to use the radius you found in order to find the volume of the bubble. In function language, if $V$ is the familiar function $V(r) = \frac{4}{3}\pi {r^3}$ giving the volume of the bubble in terms of the radius, then you first found $r(5)$, and then found $V(r(5))$.
Using the functions $r$ and $V$ as in the previous problem,
find $V(r(3))$.
find a formula, in terms of $t$, for $V(r(t))$.
Let functions $f$ and $g$ be defined as in problem 13.
Find $f(g(3))$.
Find $g(f(3))$.
Find $f(g(5))$.
Sketch a graph of $g\left( {f\left( x \right)} \right)$.
The tribble population grows exponentially, and the level of the squeaky noise they collectively make is directly proportional to the size of their population. Let the tribble functions be defined as follows:
$P$ outputs the tribble population at time $t$.
$N$ outputs the noise level produced by a given number of tribbles.
$D$ outputs the noise level given a time $t$.
Express one of these functions as a composition of the two others.
Practice
Let a function $f$ be defined by the graph below. In your notebook, sketch a graph of each of the following equations.
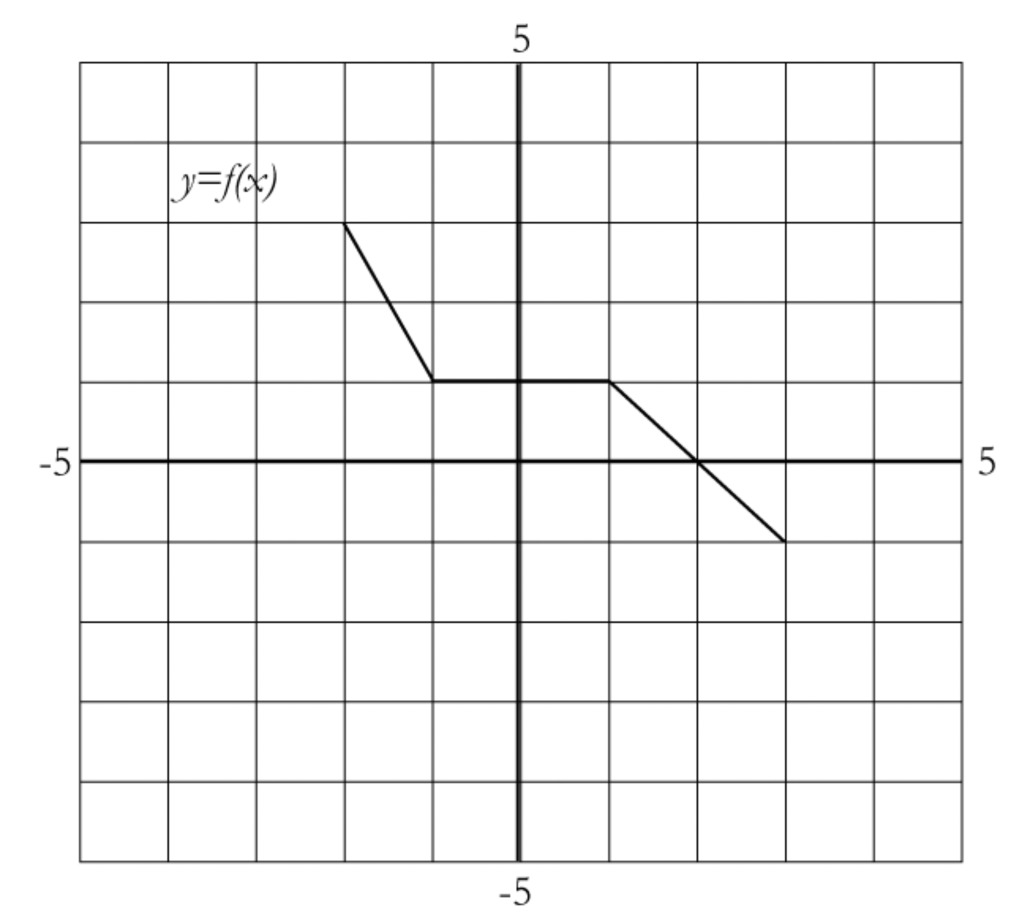
$y = f(x - 4)$
$y = f(x) - 2$
$y = f( - x)$
$y = - f(x)$
$y = f(\frac{1}{2}x)$
Without using your calculator, sketch a reasonable graph of $j(x) = \frac{1}{x}$. Identify the coordinates of three points on the graph. Then, without using your calculator, graph the following equations, including the images of the three points you identified. If the asymptotes move away from the axes, indicate them with dashed lines.
$y = j(x) + 1$
$y = j(x) - 0.5$
$y = 0.4j(x)$
$y = - 1.5j(x)$
$y = 2j(x - 2)$
Write equations for each of the graphs you sketched in the previous problem.
Each graph below is a transformation of the graph of $y = {0.5^x}$. For each graph, write an equation that models it.



Problem continued on the next page.
Let $a$ and $b$ be functions defined by their graphs below.
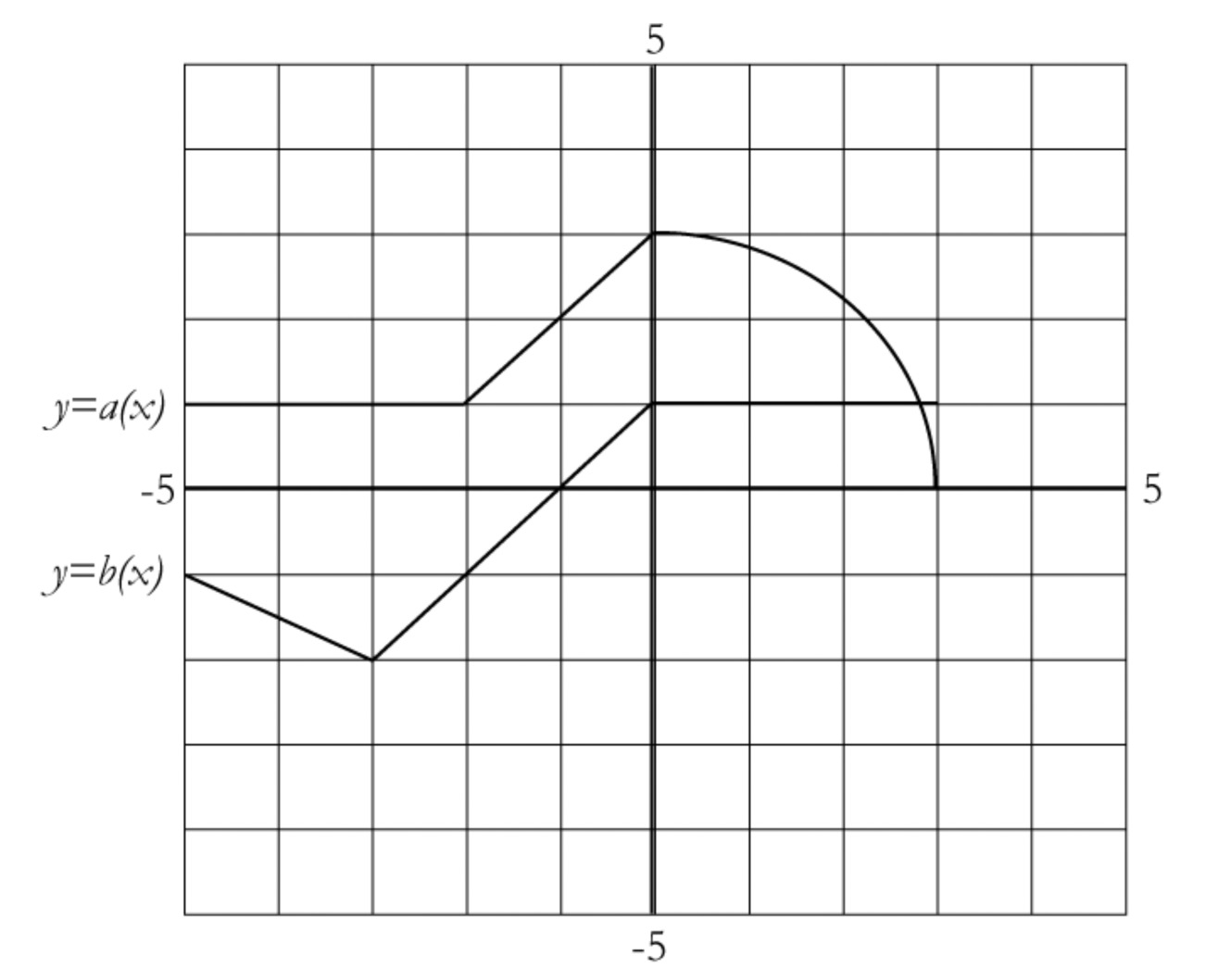
$y = a(x) + b(x)$
$y = a(x) - b(x)$
Let $f(x) = 3x$ and $g(x) = 2x + 1$. Sketch the graph of $h(x) = f(x) + g(x)$. What is its formula?
Let $c$ and $d$ be functions defined by their tables below.
|
$x$ |
0 |
1 |
2 |
3 |
4 |
5 |
|
$c$ |
5 |
-1 |
3 |
1 |
0 |
3 |
|
$d$ |
4 |
2 |
7 |
4 |
7 |
1 |
Find $c(d(3))$
Find $c(d(5))$
Find $d(c(5))$
If possible, find $c(d(2))$ and $d(c(2))$.
Let $f(x) = x^2$ and $g(x) = x^3$.
Write a formula for $f(g(x))$.
Compare your answer in part a to the formula for $f(x)g(x)$.
Give the domain…
of the square root function.
of the reciprocal function ($f(x) = \frac{1}{x}$ )
Problems
Let $f(x) = {x^2} + 2x - 8$.
Without using your calculator, graph $f(x)$ and $f(x - 2)$ on the same set of axes.
By looking at your graph, find a formula for the function $g(x) = f(x - 2)$.
Try the following alternative method for finding a formula for $f(x - 2)$: Start with the fact that $f(x - 2) = {(x - 2)^2} + 2(x - 2) - 8$, then simplify. Why should this method work?
Find a formula for $f(2x)$ if $f(x) = {x^2} + 2x - 8$. Then sketch the graph of $y = f(2x)$.
$y = f(x)$ is an exponential function that has a $y$-intercept of 2 and is asymptotic to $y = 0$. Find the $y$-intercept and asymptote of $y = - 2f(x)$.
$(2,5)$ is a point on the graph of the function $y = g(x)$. Identify the coordinates of the corresponding point on the graph of…
$h(x) = \frac{1}{2}g( - x)$.
$h(x) = - 3g(x)$.
$h(x) = 6 - g( - x)$.
$h(x) = g(x - 5) + 1$.
$h(x) = g(-2x)$.
$h(x) = c \cdot g(x) + b$.
$h(x) = -g(cx)$.
Let $g$ be the function defined by the graph below.
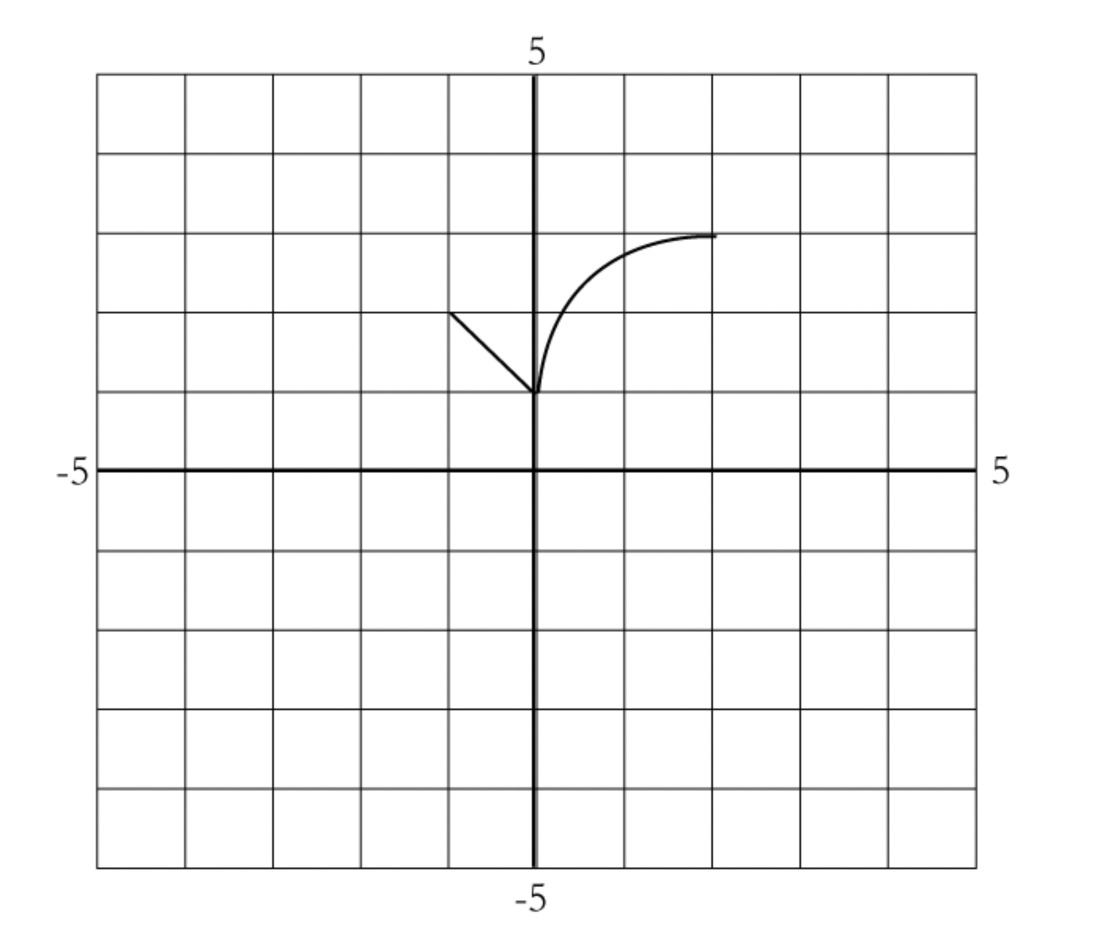
For the graphs in parts i through vi,
come up with a series of transformations that will turn the graph of g into the graph you see.
write an equation for the transformed function (for example, the first function shown below is $y = g(-x)-2$).
Let $f$ be the function defined by the graph below.
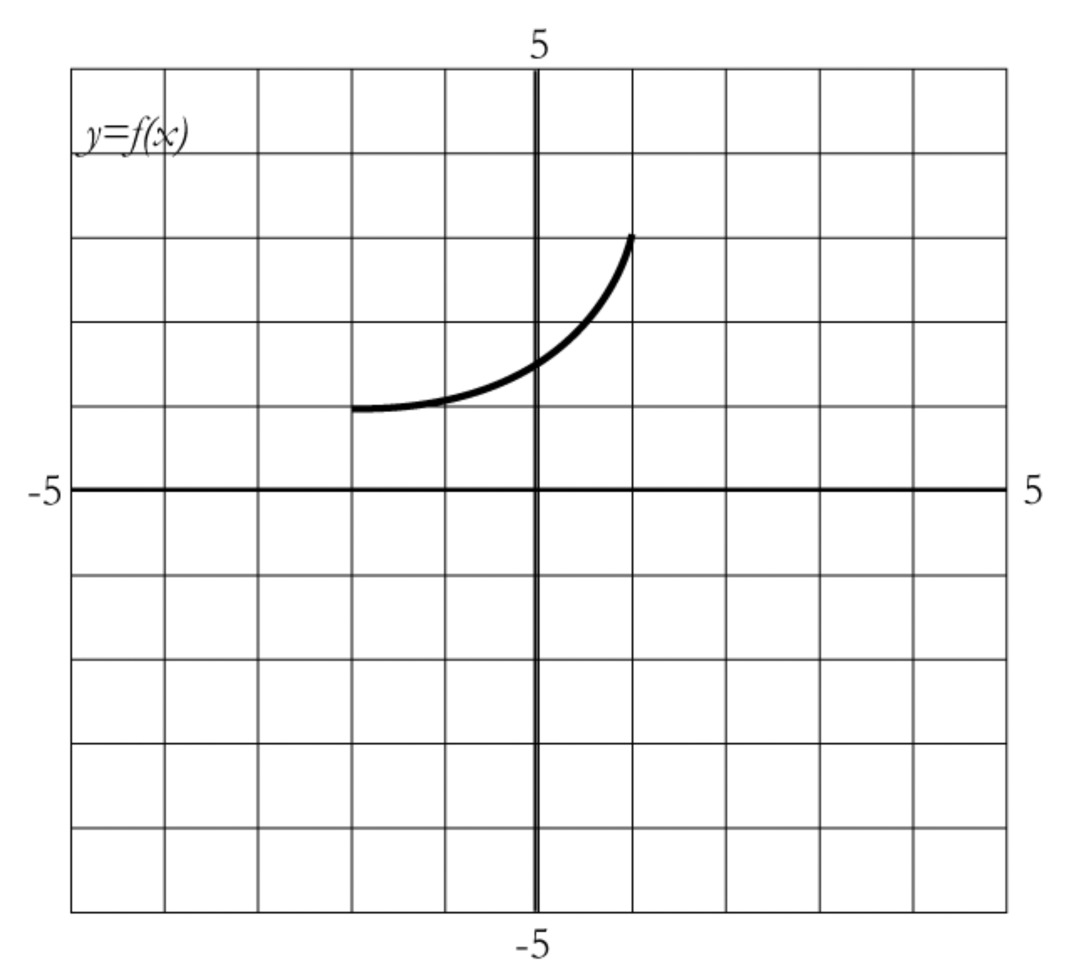
come up with a series of transformations that will turn the graph of $f$ into the graph you see.
write an equation for the transformed function.
(continuation of problem 17) When tribbles first appear on the Enterprise, there are four tribbles, collectively squeaking at a noise level of 6 decibels. Five hours after they appear on the Enterprise, there are 30 tribbles, squeaking at a noise level of 45 decibels.
Find a formula for the function giving population in terms of time, $P(t) = ...$. Assume that it is an untranslated exponential and therefore has the form $P(t) = a{b^t}$.
Find a formula for the function giving noise level in terms of population, $N(P) = ...$. (Recall that the noise level is directly proportional to the size of the tribble population.)
Now find a formula for $N(P(t)) = ...$. What does this formula tell you?
How loud will it be 24 hours after the arrival of the tribbles?
How long did it take until the noise level aboard the Enterprise reached an unbearable 150 decibels?
(Courtesy of Functions Modeling Change, Connally, et al) The number of pounds of fertilizer, $n = f(A)$, needed to fertilize a lawn is a function of the surface area $A$ of the lawn, in m$^2$. Match each story (a-c) to one expression (i-iii).
I figured out how many pounds I needed and then bought 2 extra pounds just in case.
I bought enough fertilizer to fertilize my lawn and my neighbor’s lawn, which just happens to be the size of mine.
I bought enough fertilizer to cover my lawn and my flower bed; the flower bed measures 2 square meters.
- $2f(A)$
- $f(A + 2)$
- $f(A) + 2$
Sketch the graph of $y = \left| x \right|$. The point $(0,0)$ is called the vertex of this graph.
Use transformation reasoning to predict what the graph of $y = \left| {x - h} \right| + k$ would look like, including the location of the vertex.
Investigate the effect of the constant $a$ on the graph of $y = a \left| x - h \right| + k$. Does it affect the vertex?
Without using your calculator, sketch an accurate graph of $y = \sin(\frac{\pi}{2} x)$. Include at least two periods. On the same axes, sketch the graph of $y = x$. Now, by using what you know about function addition, sketch a graph of $y = x + \sin (\frac{\pi }{2}x)$.
Sally was asked to find $a(\frac{\pi }{4})$ in the function $a(x) = \sin (x - 3) + 2$, and found the answer 0.75. Without using your calculator in any way, decide if Sally’s answer is plausible.
Earlier in this lesson, you learned that the domain of a function is the set of allowable inputs. Similarly, the range of a function is the set of outputs that a function might produce. For example, the range of the function $y = {x^2}$ is $y \ge 0$, since you can get any non-negative number you want by squaring some number, but you will never square a number and get an answer that is less than zero.
Give the range of each function.
Sally’s function $a$ from the previous problem
f(x) = $\frac{1}{x^2}$
$g(x) = {e^x}$
$h(x) = \log x$
$i(x) = {2^x} + 3$
$j(x) = \frac{1}{x}$
Give the domain and range of each function. Visual thinking is encouraged. Thinking about transformations should obviate the need for your graphing calculator.
$f(x) = \frac{1}{{x + 2}}$
$g(x) = \frac{1}{{{{(x + 2)}^2}}}$
$h(x) = \log(x+1)$
$i(x) = 2{(x - 3)^2} - 4$
$j(x) = -2\cos{x}-4$
The function $T$ graphed in the figure below gives the winter temperature in °F at a high school at time $t$ hours after midnight.
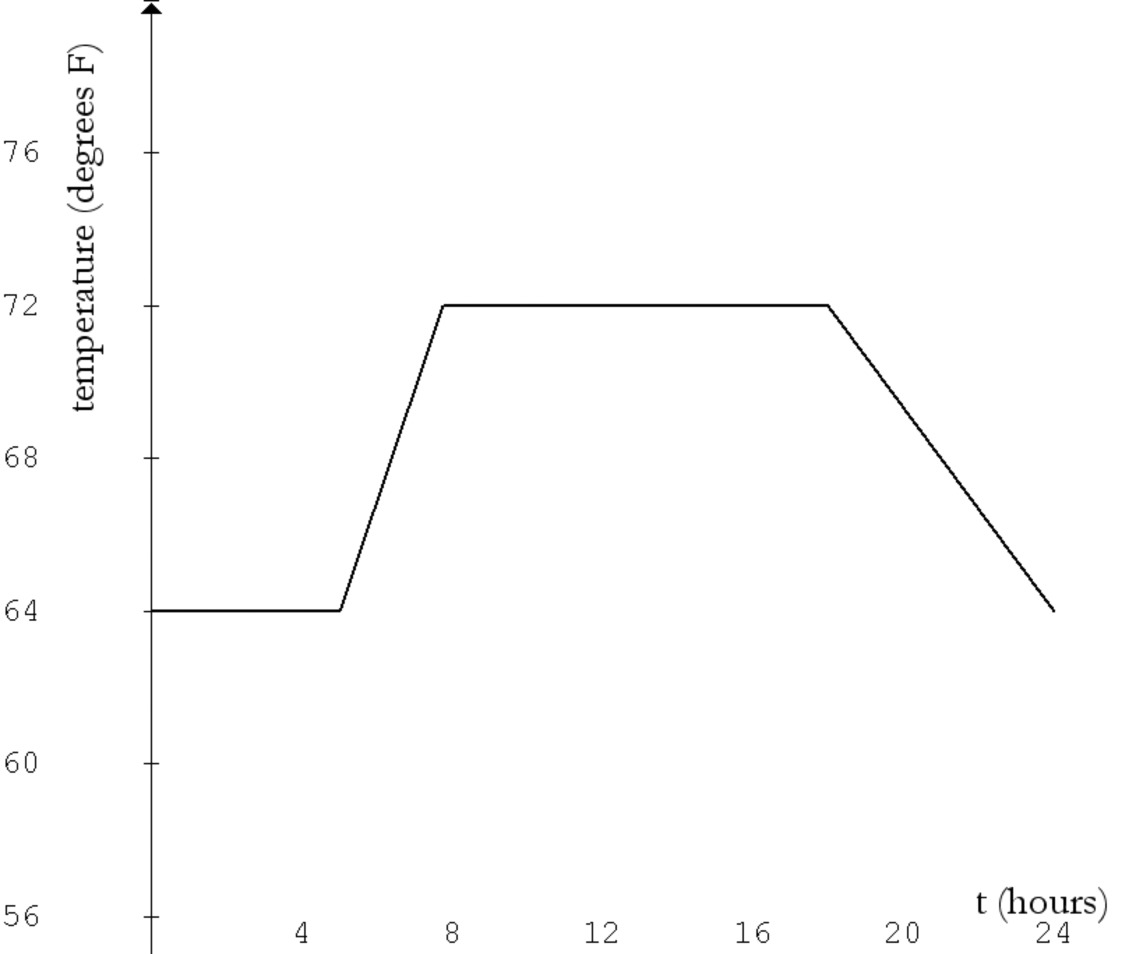
Graph $c(t) = 142 - T(t)$.
Give the range of $T$ and of $c$.
Explain why $c$ might describe the cooling schedule of the school during the summer months.
An investigation into slope…
Find the slope of the line that heads in the same direction as the curve defined by $y = \log x$ at the point (10,1).
Make a prediction about the slope of the line heading in the same direction as the curve defined by $y = 3\log x$ at the point (10,3), and see if you are right.
Don’t use a calculator for this problem.
Solve: $\frac{2}{{x - 1}} = x + 3$
Evaluate: ${\log _2}{4^7}$
By what factor does $\frac{{{w^5}{x^2}}}{{{y^3}{z^7}}}$ increase if $w$ doubles and $y$ is halved?
Solve for $x$: $\sqrt {4x} + x = 3$
Find all values of $x$ so that
The greatest integer function takes an input and outputs the greatest integer that is less than or equal to that input. The greatest integer of $x$ is written $\left\lfloor x \right\rfloor$. Here are some examples: $\left\lfloor 2.7 \right\rfloor=2$, $\left\lfloor -4.5 \right\rfloor= –5$, and $\left\lfloor5\right\rfloor=5$.
Sketch a graph of the greatest integer function. When you’re done, ask your teacher about “open circle” notation.
Find the domain and range of the greatest integer function.
The greatest integer function is nicknamed the “floor function,” which suggests the existence of a “ceiling function.” The ceiling function takes an input and outputs the least integer greater than $x$. “Ceiling of $x$” is written $\left\lceil x \right\rceil$.
Sketch a graph of $y = \left\lceil x \right\rceil$.
Write a formula for $\left\lceil x \right\rceil$ in terms of $\left\lfloor x \right\rfloor$. Is one graph a translation of the other?
Sketch a graph of $y = \left\lfloor x \right\rfloor + {x^2}$ for $ - 2 \le x \le 2$.
Define the signum function as follows: ${\mathop{\rm sgn}} (x) = 1$ if x is positive, -1 if $x$ is negative, and 0 if $x = 0$. Sketch the graph of…
$y = {\mathop{\rm sgn}} (x)$
$y = {\mathop{\rm sgn}} (x) - 2$
$y = {\mathop{\rm sgn}} (x) + 1$
$y = {x^2} + {\mathop{\rm sgn}} (x)$
The function © tells you how many siblings someone has, so ©(Malia Obama)=1 and ©(Chelsea Clinton)=0.
Find ©(you).
Give the domain and range of the function ©.
The function $ \uparrow$ has the formula $ \uparrow(x) = {x^2} + 1$. Which makes sense: $©(\uparrow(x))$ or $\uparrow(©(x))$?
Below are tables for three functions, $f$, $g$, and $h$. These tables are complete tables — that is, the functions are not defined for any inputs other than the inputs given here.
|
$x$ |
-5 |
-2 |
1 |
2 |
3 |
7 |
| $f(x)$ |
2 |
1 |
2 |
3 |
1 |
7 |
|
$x$ |
0 |
1 |
2 |
3 |
4 |
5 |
|
$g(x)$ |
-5 |
1 |
3 |
7 |
2 |
-2 |
| $x$ |
-3 |
0 |
1 |
2 |
3 |
7 |
| $h(x)$ |
0 |
1 |
2 |
3 |
4 |
5 |
Which compositions of functions are possible? That is, can you compute $f(g(x))$ for all values of $x$? How about $g(f(x))$? Find all pairs that work, paying attention to order.
Choose one of the compositions from part a and make a table of values for it.
Does $f(f(x))$ exist? How about $g(g(x))$ or $h(h(x))$?
An investigation into composing functions…
Make up tables for two functions, $f$ and $g$, such that $h(x) = f(g(x))$ exists. Then make a table for the function $h$.
How do the domain and range of the function $h$ relate to the domain and range of the functions $f$ and $g$?
What (helpful) advice would you give to someone else in the class if they were trying to come up with two functions that could be composed?
Let the function a be defined by the graph below.

Sketch the graph of $y = \left| {a(x)} \right|$.
Sketch the graph of $y = a \left( \left| {x} \right| \right)$.
Let the function b be defined by the graph below.
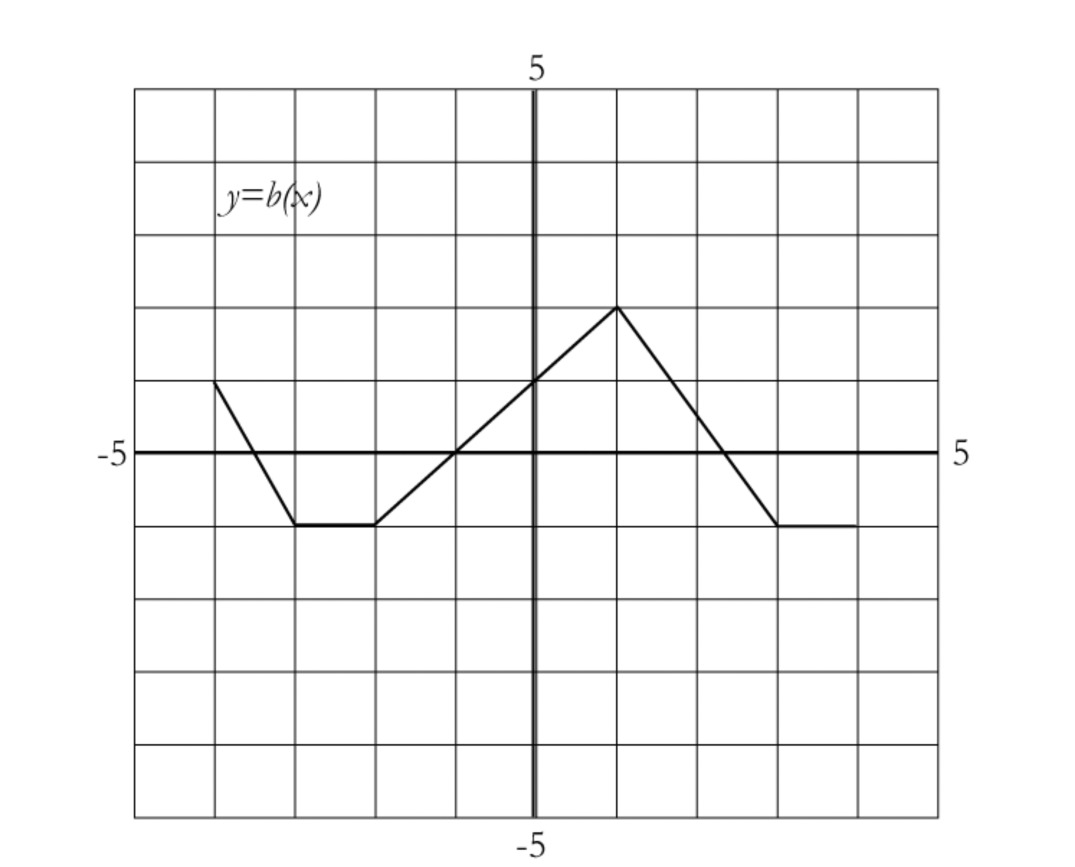
Sketch the graph of $y = - \left| {b(x)} \right|$.
Sketch the graph of $y = b(\left| { - x} \right|)$.
Plot the graph of a function where, for all $x$, $f( - x) = f(x)$. Use the domain $ - 5 \le x \le 5$.
Plot the graph of another function that meets the criteria given in part a.
Make a conjecture about the graph of any function for which $f( - x) = f(x)$
Plot the graph of a function where, for all $x$, $f( - x) = - f(x)$. Use the domain $ - 5 \le x \le 5$.
Plot the graph of another function that meets the criteria given in part a.
Make a conjecture about the graph of any function for which $f( - x) = - f(x)$.
Are there any standard functions you know of that have the properties you conjectured in problems 52 and 53? What are they?
Plot the graph of function where, for all $a$ and $b$, if $f(a) = b$, then $f(b) = a$. For example, if $f(2) = 4$, it must also be true that $f(4) = 2$. Use a domain of $ - 5 \le x \le 5$.
Plot the graph of another function that meets the criteria given in part a.
Make a conjecture about the graph of any function for which $f(a) = b$ implies $f(b) = a$. If necessary, make up more examples to test or refine your conjecture.
Let the function $g$ be defined by the following chart.
|
$x$ |
-1 |
0 |
0.5 |
1 |
2 |
3 |
4 |
|
$g(x)$ |
-4 |
-3 |
-1 |
1 |
1.5 |
2 |
4 |
Plot the points on a graph.
From the information you have, make a table and graph of the inverse function for g. The standard notation for this function is “${g^{ - 1}}$,” read “$g$ inverse.”
Describe any patterns you notice.
The graph of ${g^{ - 1}}$ is a transformation of the graph of $g$. Describe this transformation in precise language.
Find a formula for the inverse function of $f(x) = {x^3}$, and graph both $f$ and ${f^{ - 1}}$ on your calculator. Is the transformation you see the same one as in the previous problem? What evidence do you have for this?
The function $f$ from problem 1 does not have an inverse. Why not? Does the function $g$ from problem 13 have an inverse?
Which functions below DO have inverses?
$f(x) = {x^2}$
$g(x) = \sqrt x $
$h(x) = {x^3}$
$i(x) = {2^x}$
$j(x) = {x^6}$
Which functions graphed below have inverses?
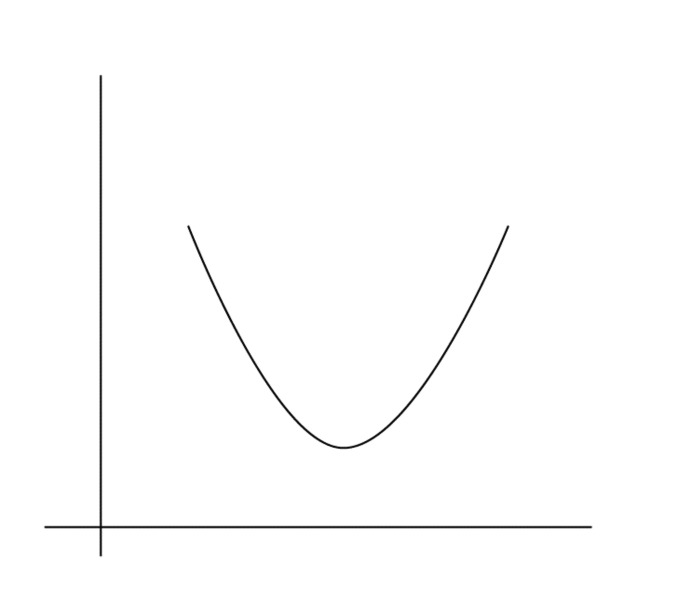

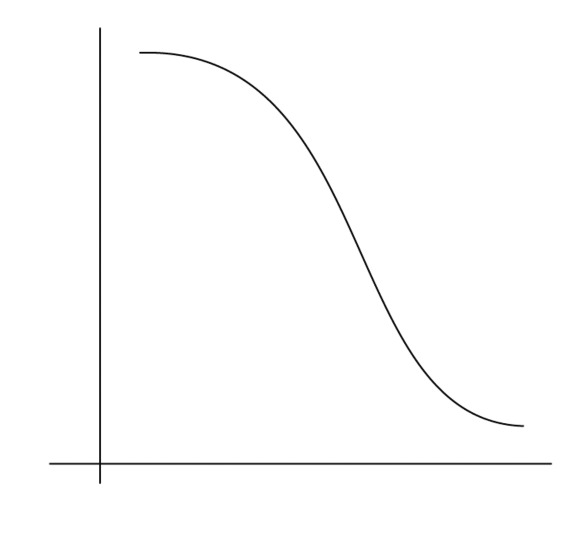
Continued on the next page
The following questions refer to the function sketched below.
Find the domain and range of the function
Sketch the inverse of the function on the same axes
Find the domain and range of the inverse.
Find the domain and range of
$f(x) = {2^x}$
$g(x) = {\log _2}x$
The radius of a circle is initially 3 cm. It increases by two centimeters each hour.
Find a formula for the area of the circle in terms of time.
Sketch three graphs, labeling the axes appropriately:
$y = r(t)$ (radius of the circle vs. time)
$y = A(r)$ (area of the circle vs. radius), and
$y = A(t)$ (area of the circle vs. time).
When the circle has a radius of 7 cm, what is the rate of change of the area of the circle with respect to the radius? Make sure that your answer includes units.
At time t = 2 hours, what is the rate of change of the area of the circle with respect to time? Make sure that your answer includes units.
Exploring in Depth
Graph $f(x) = {x^2}$ and $g(x) = 2x$ on the same axes.
Make a rough sketch of what you think a graph of $y = f(x) + g(x)$ would look like. Then see if you are right by graphing the function $y = {x^2} + 2x$ .
Using the techniques of this lesson, write an equation for the graph you drew in part a. Is the equation equivalent to $y = {x^2} + 2x$?
Graph the linear function $f(x) = 2x - 6$.
Reflect the line you’ve drawn over the line $y = x$.
Find an equation for the reflected line. Verify that it is the graph of ${f^{ - 1}}$ .
If $f$ and $g$ are inverse functions, find $f(g(x))$.
Let $f(x) = {x^2}$, $g(x) = x - 2$, and $h(x) = 5x$. Write each of the following functions as a composition of $f$, $g$, and/or $h$.
$a(x) = 5(x - 2)$
$b(x) = 5{x^2}$
$c(x) = {x^2} - 2$
$d(x) = {(5x)^2} - 2$
$e(x) = 5{(x - 2)^2}$
$z(x) = (5x - 2)^2$
Find the domain and range of each function.
$a(x) = \sqrt{x - 5}$
$b(x) = \sqrt {{x^2} + x - 6} $
$c(x) = \frac{{x + 5}}{{x - 3}}$
$d(x) = \frac{{{x^2}}}{{(x + 1)(x - 2)}}$
$e(x) = -x^2 - 7$
$f(x) = \frac{{3x}}{x}$
You have been using the “inverse sine” function for years, but thinking about it now, you can see that the sine function does not have an inverse! There are many ways to get an output of 1: when $x$ is 90°, 270°, 450°, etc if you are working in degrees, or when x is $\frac{\pi }{2}$, $\frac{{3\pi }}{2}$, $\frac{{5\pi }}{2}$, etc if you are working in radians. Thus, if someone says, “find ${\sin ^{ - 1}}1$,” you wouldn’t know which of the values listed above to give in response.
The reason we can still talk about the inverse sine function is that we are thinking about only a limited set of inputs (angles) that you can plug in to the function $f(x) = \sin x$. Limiting the allowable inputs in this way is called a domain restriction.
Use your calculator to take the inverse sine of some angles. Notice the kinds of outputs it gives you. Can you figure out exactly which angles belong to the restricted domain of the sine function?
In your notebook, sketch a graph of the sine function, showing a few periods, and show in bold the part of the graph that is produced by using inputs from the restricted domain. Does the restriction seem like a logical choice? Would there be other ways to do it?
Do the ${\cos ^{ - 1}}$ and ${\tan ^{ - 1}}$ functions use the same domain restriction as ${\sin ^{ - 1}}$? Play around with your calculator to see. If not, what are the other domain restrictions?
Let $f(x) = \sqrt x $ and $g(x) = {x^2}$. Do $f(g(x))$ and $g(f(x))$ have the same domain? First answer the question by looking at the algebra, then check your answer by having your calculator graph the unsimplified formula for each composition.
Let $f(x) = 2x$ and $g(x) = \sqrt {16 - {x^2}} $.
Find $f(g(x))$ and $g(f(x))$.
Give the domain and range of each of the functions in part a.
Let $f(x) = {x^2}$ and $g(x) = 4 - x$.
Find $f(g(x))$ and $g(f(x))$ .
Give the domain and range of each of the functions in part a.
Trigonometric functions are not the only common functions that require a domain restriction in order to take their inverse. $f(x) = {x^2}$ does not have an inverse because for a given output, like 4, there are multiple inputs, -2 and 2, that produce that output. However, if you restrict the domain of $f$ to allow only values of $x$ greater than or equal to zero, then the function has an inverse. You can think of the square root function as the inverse of $f(x) = {x^2}$ on this restricted domain.
For each function below, suggest a domain restriction that would allow the function to have an inverse.
For functions i, ii, and iii, find an equation for the inverse of the function (with its domain suitably restricted).
$a(x) = {(x - 4)^2} + 3$
$b(x)=\frac{1}{x^2}$
$c(x) = \frac{1}{{{{(x + 3)}^2}}}$
-

If $g(x) = \cos x$, find (using no calculator)…
$g(g^{-1}(\frac{1}{2}))$
${g^{ - 1}}(g(45^\circ ))$
$g^{-1}(g(37^\circ))$
Will it always be true that…
$\cos ({\cos ^{ - 1}}a) = a$?
${\cos ^{ - 1}}(\cos a) = a$?